Enhancing the electron pair approximation with measurements on trapped-ion quantum computers

Abstract

The electron pair approximation offers an efficient variational quantum eigensolver (VQE) approach for chemistry simulations on quantum computers. With the number of entangling gates scaling quadratically with system size and a constant measurement overhead, the orbital optimized unitary pair coupled cluster double (oo-upCCD) ansatz strikes a balance between accuracy and efficiency. However, the electron pair approximation prevents the method from achieving quantitative accuracy. To improve it, we explore the theory of second order perturbation (PT2) correction to oo-upCCD. PT2 accounts for the missing broken-pair contributions in oo-upCCD, while retaining its efficiencies. For molecular bond stretching and chemical reactions, the method significantly improves the predicted energy accuracy, reducing oo-upCCD’s error by up to 90%. On IonQ’s quantum computers, we find that the PT2 energy correction is highly noise-resilient. The predicted VQE-PT2 reaction energies are in excellent agreement with noise-free simulators after applying simple error mitigations solely on the VQE energies.

Introduction

Quantum computers have the potential to revolutionize a number of fields, including physical simulation¹, optimization², and machine learning³. Of particular interest is to solve the electronic structure problem of molecules and materials using quantum computers. It is well known that classically computing exact solutions to the electronic structure problem requires computational resources that grow exponentially with system size. To mitigate this problem, the current state of the art is to use polynomial scaling approximate methods to predict electronic properties. One example is the “gold standard” of electronic structure theory, projected coupled-cluster theory⁴, namely CCSD(T).

In contrast, quantum algorithms unlock the potential to solve the exact electronic structure problem to arbitrary accuracy in polynomial space and time. Unfortunately, known algorithms with robust theoretical guarantees (such as phase estimation) remain highly sensitive to noise, and therefore require fault-tolerant quantum computers with error-correction capabilities. Given that fault-tolerant quantum devices are not yet available, there is a significant focus on developing algorithms that are resistant to noise and can accurately determine electronic properties. The ultimate goal is to enable reliable predictions of various molecular properties, including energy levels, conformational energies and geometries, binding affinities, and response properties. Access to robust and dependable predictions promises to contribute to the systematic development in areas like functional materials⁵, next-generation batteries⁶, pharmaceutical discovery⁷, and novel catalysts⁸. Consequently, the potential benefits of quantum computing in these areas are considerable.

In recent years, significant progress has been made in quantum technologies, marked by advancements in both algorithmic methods and hardware capabilities. Presently, a variety of cloud-based quantum computing platforms are available, offering access to quantum processors with diverse architectures. These platforms, provided by several commercial cloud vendors, offer a variety of computational capacities, allowing the user to choose between systems with varying qubit connectivities, gate operation times, fidelity measures, and qubit counts. This hardware expansion has been matched by a similarly rapid development of algorithms for quantum chemistry simulations, now increasingly implemented and tested on these emerging quantum computing systems.

In addition to cloud-accessible quantum computing platforms, the quantum computing community has developed and refined algorithmic approaches to address some of the most pressing challenges in the field. Since the original proposal of using the quantum phase estimation (QPE)^9,10 approach to estimate ground state energies of molecules, researchers have developed even more efficient implementations, introducing advances such as qubitization^11,12 and leverage factorization methods such as tensor hypercontraction¹³. These efforts underscore the dynamic interplay between advances in both algorithm design and hardware capability for applications to quantum chemistry.

In this context, understanding resource needs has become especially important for the quantum community. Researchers have provided numerous resource estimates^7,8,14,15 for the compute time and number of qubits required to solve some of the hardest chemical problems with the precision that only a fault-tolerant quantum computer can achieve. While these resource estimates are a crucial step towards understanding the full potential of quantum computing, the practical realization of these solutions remains contingent on the development of broadly accessible (and useful) fault-tolerant quantum computers.

Currently, quantum devices operate within the era of noisy intermediate-scale quantum (NISQ)^16,17 computing. In the NISQ era, quantum computers face limitations in the number of utilizable qubits and the fidelity of quantum gates. For example, the Aria quantum computer developed by IonQ has 25 qubits with a two-qubit gate fidelity of 99.4%. Despite the high fidelity, the chance of error remains nonzero and this limits the number of operations that can be performed reliably on QPUs. This in turn limits the design and application of quantum algorithms.

Developing algorithms that are noise-resilient on NISQ systems has drawn significant attention, and remains of utmost importance in the near term. For chemistry, the variational quantum eigensolver (VQE)^{18,19,20,21,22,23} and its variants represent a class of particularly promising NISQ algorithms. VQE utilizes parametrized quantum circuits, known as ansatze, to estimate electronic wave functions. It employs the variational principle to optimize these parameters so as to locate the energy minimum. This minimum represents the optimal approximation of the exact wave function, within the limits of the parametrized circuit. VQE offers users the choice of an ansatz to strike a balance between accuracy and fidelity. Simpler ansatze lead to more efficient, shallower circuits, which are amenable to NISQ systems. However, they may lack the expressiveness to capture accurate chemical behaviors. Conversely, complex ansatze can improve accuracy, but their effectiveness is often diminished by noise as a consequence of compounding numerous qubit operations. Therefore, given a certain number of qubits and gate fidelities, users must carefully design VQE circuits to strike a balance between accuracy and fidelity.

The potential quantum advantage of VQE is that it allows the efficient utilization of ansatze that are inefficient to compute classically, such as the unitary coupled cluster (UCC) ansatz^{18,19,24,25,26}. The UCC class of ansatze is known to offer more accurate energy predictions to its classical (projective) counterpart, especially for strongly correlated systems. However, as with the classical case, care must be given to the design and selection of the UCC-based ansatz depending on the chemical case at hand.

We recently developed a resource-efficient VQE algorithm²⁷ for quantum chemistry simulations. This algorithm takes advantage of the unitary pair coupled cluster doubles (upCCD)^28,29,30 ansatz. In the upCCD ansatz, all the electrons are paired, which allows each electron pair to be treated as an effective (hard-core) bosonic particle. Computationally, this allows one to map spatial orbitals to individual qubits. In doing so, the number of qubits required are reduced by half compared to the conventional Jordan-Wigner mapping of spin orbitals to qubits. In previous work, we demonstrated that the upCCD ansatz yields highly efficient circuits with a constant overhead for energy measurements. We further showed that the orbital optimization (oo) effects, which are crucial for modeling bond-breaking scenarios, could be applied to the upCCD circuit for no additional quantum cost, in the sense that there is no increase in either the circuit depth or the number of measurements beyond the additional macro-iterations for the orbital optimization loop. Preliminary results from using the oo-upCCD ansatz on IonQ’s trapped-ion quantum computer show that the predicted relative energies are in excellent agreement with a noiseless quantum simulator.

Despite this progress, it is important to note that the oo-upCCD ansatz can only achieve quantitative levels of accuracy in two-electron problems. This limitation arises because it confines electrons to pairs, thereby neglecting the typically substantial correlation energy contribution from broken-pair excitations. Consequently, addressing how to incorporate broken-pair contributions into the oo-upCCD framework is a pressing challenge. One approach is to introduce these excitations through quantum circuits. However, this would compromise two major benefits of the oo-upCCD ansatz: 1) efficient mapping of spatial orbitals to qubits, and, 2) constant energy measurement overhead. Moreover, this method would significantly increase the circuit depth, even if using optimal circuit compilation techniques³¹.

In this study, we pursue an alternative approach by first computing the reduced density matrices (RDMs) of the oo-upCCD circuits. From these RDMs, we leverage a second-order perturbation theory (PT2) framework to calculate the energetic contributions from broken-pair excitations. This method does not add to the circuit depth and maintains a constant energy measurement overhead. We apply this technique to model bond dissociation and chemical reactions using quantum simulators and IonQ’s trapped-ion quantum computers. Our objectives are twofold: to determine the accuracy achievable using oo-upCCD with a perturbative correction, as well as assess the performance of the perturbative algorithm on current quantum computing hardware.

The paper is organized as follows: we start by introducing the oo-upCCD ansatz and its circuits, followed by an exploration of the second-order perturbation theory applied to this ansatz. In particular, we discuss the zeroth-order Hamiltonian, wave function correction, and derivation of the working equations for the energy corrections. Numerical results are presented on quantum simulators and IonQ’s Aria and Forte quantum computers for potential energy surface predictions of N₂, Li₂O, and two chemical reactions. We conclude with a summary of our findings and comments on future directions.

Readers are strongly encouraged to read the “Methods” section before the “Results” section. In “Methods,” we describe the details of the quantum computer hardware used to run the experiments, as well as a detailed derivation of the working equations for the algorithmic implementation. Moreover, the mathematical notation defined in the “Methods” section is consistently used throughout the “Results” section.

Results

The oo-upCCD Ansatz

The unitary pair coupled-cluster double (upCCD) ansatz is

$$\vert {\Psi }_{{\rm{u}}{\rm{pCCD}}}\rangle ={e}^{T-{T}^{\dagger }}\left\vert {\rm{HF}}\right\rangle$$

(1)

in which T is the pair-double cluster operator, defined as

$$T=\sum _{ia}{t}_{i}^{a}{a}_{a\alpha }^{\dagger }{a}_{a\beta }^{\dagger }{a}_{i\beta }{a}_{i\alpha }$$

(2)

in which i and a are indices for occupied and unoccupied orbitals in the HF state. ${a}_{p\alpha }^{\dagger }$ (${a}_{p\beta }^{\dagger }$) and a_pα (a_pβ) are the fermionic creation and annihilation operators in the p-th spin-up (α) or spin-down (β) orbital.

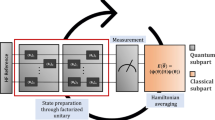
The exponentiation of the pair-excitation operator can be efficiently implemented with the following circuit, given in Fig. 1. Once the circuit is defined, one needs to measure the energy expectation value $\langle{\Psi }_{{\rm{upCCD}}}| H| {\Psi }_{{\rm{upCCD}}}\rangle$ for the second-quantized Hamiltonian H. In the full electronic Hamiltonian, H contains O(N⁴) terms, with N being the number of qubits. Yet, owing to pair symmetry, most of these terms do not contribute to the energy within the upCCD approximation. After removing these pair-breaking terms, one finds that only three measurements are needed (in the Pauli X, Y, and Z basis, respectively) to compute the energy. Moreover, the number of basis measurements is independent of problem size, and three circuits are all that is needed for any upCCD energy evaluation.

Fig. 1: A quantum circuit that implements the Givens rotation.

S is the phase gate. H is the Hadamard gate. $R_{y}(\theta)$ is the single qubit Y-rotation gate by angle $\theta$. Entangling gates are $CNOT$ gates.

One potential concern is that the upCCD ansatz defined in Equation (1) is not invariant to the choice of underlying orbitals. Previous studies^28,30,32,33 on similar wave functions have found that it is necessary to optimize the orbitals along with the cluster amplitudes, especially for strongly correlated systems. The orbital optimized upCCD ansatz is

$$\vert{\Psi }_{{\rm{oo}}-{\rm{upCCD}}}\rangle ={e}^{K}{e}^{T-{T}^{\dagger }}\left\vert {\rm{HF}}\right\rangle$$

(3)

in which there are two different sets of parameters: 1) circuit parameters in the cluster operator T, and, 2) orbital rotation parameters in the the orbital rotation operator K, which is defined as

$$K=\sum _{p > q}\sum _{\sigma }{K}_{pq}({a}_{p\sigma }^{\dagger }{a}_{q\sigma }-{a}_{q\sigma }^{\dagger }{a}_{p\sigma })$$

(4)

Here K is an anti-Hermitian matrix and σ indexes the spin.

The VQE perturbation theory

As mentioned previously, the cluster operator in upCCD does not contain any broken-pair excitations. This is because in the cluster operator defined in Equation (2), the α and β electron creation and annihilation operators are restricted to occupy the same orbitals. As a result, terms such as ${a}_{a\alpha }^{\dagger }{a}_{b\beta }^{\dagger }{a}_{j\beta }{a}_{i\alpha }(i\,\ne\,j,a\,\ne\,b)$ are not included. By neglecting these terms, we observe a quantitative deviation from the exact energy. To remedy this, we would like to recover the energetic corrections from these terms. To account for the broken-pair contributions we use perturbation theory as follows. We first partition the molecular Hamiltonian as

$$H={H}_{0}+\lambda V$$

(5)

in which H₀ is a simple non-interacting Hamiltonian and V accounts for the electron interaction. λ is the scale of the interaction.

We then write the energy and wave function in terms of λ

$$\begin{array}{l}\left\vert \Psi \right\rangle =\left\vert {\Psi }^{(0)}\right\rangle +\lambda \left\vert {\Psi }^{(1)}\right\rangle +{\lambda }^{2}\left\vert {\Psi }^{(2)}\right\rangle +\cdots \\ E={E}^{(0)}+\lambda {E}^{(1)}+{\lambda }^{2}{E}^{(2)}+\cdots \,.\\ \end{array}$$

(6)

Plugging the wave function and energy into the time-independent Schrödinger’s equation, and matching terms up to second order, one could derive the working equation for VQE-PT2. The second-order energy correction becomes

$${E}^{(2)}=\mathop{\sum }\limits_{P}^{{\rm{non-pair}}}{t}_{P}\left\langle {\Psi }^{(0)}| V| {\Psi }_{P}\right\rangle$$

(7)

in which P is a compounded index for a pair-breaking single or double excited configuration, and t_P is computed by solving,

$$\sum _{P}{G}_{PQ}{t}_{P}=-{Y}_{Q}$$

(8)

where we define

$$\begin{array}{l}{G}_{PQ}=\left\langle {\Psi }_{Q}| {H}_{0}| {\Psi }_{P}\right\rangle -{E}^{(0)}\left\langle {\Psi }_{Q}| {\Psi }_{P}\right\rangle \\ {Y}_{P}=\left\langle {\Psi }_{P}| V| {\Psi }^{(0)}\right\rangle \end{array}$$

(9)

in which the G matrix and the $\overrightarrow{Y}$ vector are measured on quantum computers. The readers are strongly encouraged to read the “Method" section to find an in-depth explanation of the VQE-PT2 working equations derivations. The method for efficient construction of these quantities, as well as a regularization method to address the numerical instability of these equations, are provided in the Supplementary Information.

Numerical results on molecular dissociations

We begin our numerical results with the dissociation of the N₂ triple bond. In Fig. 2, we compare the energy predicted by restricted Hartree-Fock (RHF), oo-upCCD, oo-upCCD-PT2, and full configuration interaction (FCI). We observe that the oo-upCCD energy provides a significant improvement over RHF, but it remains far from the FCI energy. This is due to the missing broken-pair excitation contributions in the oo-upCCD wave function. After applying the perturbation correction, we find that it is now much closer to FCI. The nonparallelity error (NPE) defined as the difference between the largest and smallest error with respect to FCI along the potential surface, is reduced from 52 mH to 14 mH, which demonstrates the effectiveness of the perturbation correction.

Fig. 2: Potential energy surface for the dissociation of the N₂ molecule in the STO-3G basis computed with RHF, oo-upCCD, oo-upCCD-PT2, and FCI.

VQE results are obtained from a noise-free simulator.

Our second example is the symmetric dissociation of the Li₂O molecule. Li₂O is one of the secondary reaction products in lithium-air batteries, which is a potential candidate for next-generation lithium battery due to its high energy density. The results on an ideal simulator are shown in Fig. 3, comparing RHF, FCI, oo-upCCD, and oo-upCCD-PT2. As one could see, similar to the N₂ dissociation, the oo-upCCD-PT2 significantly improves the accuracy of oo-upCCD, and reduces the NPE vs FCI from 69 mH to 24 mH. This is particularly true in the equilibrium geometry. When bonds are stretched, oo-upCCD-PT2 still exhibits some noticeable amount of errors compared to FCI. These remaining errors are due to the limitation of the chosen form of the second order perturbation theory, such as 1) higher order terms are needed 2) one needs to use a different zeroth-order Hamiltonian than the simple one-body one we use. 3) the diagonal approximation of the G matrix.

Fig. 3: Potential energy surface for the symmetric dissociation of the Li₂O molecule in the STO-3G basis computed with RHF, oo-upCCD, oo-upCCD-PT2, and FCI.

VQE results are obtained from a noise-free simulator.

Numerical results on chemical reactions

We now move our attention to the chemical decomposition process of the CH₂OH⁺ → HCO⁺+H₂ and the S_N2 reaction CH₃I + Br⁻ → CH ₃Br + I⁻. The simulated energy profile along the reaction path is shown in Fig. 4 for the CH₂OH⁺ decomposition. After freezing the core orbitals, the remaining eleven spatial molecular orbitals are mapped to eleven qubits. Unsurprisingly, oo-upCCD without perturbative corrections is insufficient to produce quantitative accuracy for absolute energies, capturing roughly only 50% of correlation energy. However, due to error cancellation, the predicted reaction energy barrier (209 mH) is close to FCI (202 mH). The energy difference between reactants and products (ΔE) is predicted to be 50 mH by oo-upCCD, which overestimates the FCI prediction (38 mH) by 24%. Applying the PT2 correction significantly improves the results, and we are able to capture 88% of the correlation. The predicted reaction energy barrier and ΔE is 205 mH and 39 mH respectively, which reduces the original oo-upCCD error by 57% and 92%.

Fig. 4: The simulated CH₂OH⁺ → HCO⁺+H₂ reaction energy pathway using RHF, oo-upCCD, oo-upCCD-PT2, and FCI.

VQE results are obtained from a noise-free simulator. The zero of the energy is set to the FCI reactant state.

The simulated results of the S_N2 reaction of CH₃I + Br⁻ are shown in Fig. 5. After freezing the core orbitals, we are left with 15 spatial orbitals—therefore, 15 qubits—to simulate. Working in this active space, we compare with classical complete active space configuration interaction (CASCI) calculations. Similar to the CH₂OH⁺ decomposition, the perturbation correction brings the oo-upCCD energy much closer to the CASCI predictions. Besides absolute energies, relative energies are also improved. The predicted barrier height is 14 mH by oo-upCCD-PT2 vs 10 mH by CASCI, which reduces the error of oo-upCCD (19 mH) by 50%.

Fig. 5: The simulated CH₃I + Br⁻ → CH ₃Br + I⁻ S_N2 reaction reaction energy pathway using RHF, oo-upCCD, oo-upCCD-PT2, and FCI.

VQE results are obtained from a noise-free simulator. The zero of the energy is set to the FCI product state.

Motivated by the success of perturbation theory for oo-upCCD in quantum simulators, we performed these chemical reaction simulations on two generations of the IonQ’s quantum computers. We simulate reaction steps 0, 50, and 140 of the CH₂OH⁺ decomposition process on the Aria QPU. These three points correspond to the reactants, transition state, and products, respectively. We first perform a circuit pruning process, in which gates whose parameters are below a chosen threshold are removed from the circuit. In our experience, the minor energy benefits derived from these small-parameter quantum operations are overshadowed by the introduction of system noise. In our study, we choose the threshold to be 0.04 radians. The pruned circuits have 10 CX gates and 46 single qubit gates. The experimental results are shown in Fig. 6. As expected, depolarizing hardware noise yields a systematic, positive bias to the total energy. This can be alleviated by applying a constant shift to the energy. In this case, we shift by a constant 364 mH, which is obtained by computing the average energy error between the simulator and the quantum computer for these three structures. As we have demonstrated in a previous study²⁷, in the small error regime, the errors lead to a positive bias in the measured VQE energy, and the bias is consistent across different geometries. Due to this consistency, the predicted relative energies are indeed very accurate. After applying this shift, the experimental results roughly match the prediction of the noiseless simulator. This suggests that the hardware errors are consistent across reaction steps and the relative energy is not affected.

Fig. 6: The simulated CH₂OH⁺ → HCO⁺+H₂ reaction energy pathway on the IonQ Aria quantum computer.

The zero of the energy is set to the CASCI reactant state. Data markers are staggered for legibility, and error bars correspond to a statistical error of ± 1 standard error.

Although it is tempting to consider the shifted energies as a form of error mitigation, we note that the exact shift requires the availability of noiseless simulation results, which is generally not the case for circuits that are not classically simulatable. Therefore, one should think of the shift as merely a way to demonstrate that the relative energies—which are of more utility in practice—are still accurate despite the presence of noise.

The total energy of oo-upCCD-PT2 contains two parts: the oo-upCCD energy (E_VQE) and the energy correction (E⁽²⁾). Table 1 shows the energy contributions from these two parts comparing the statevector simulator and the Aria QPU, and we find that almost all the errors in energy are from the the oo-upCCD energy term. This could be understood in two ways. First, the magnitude of the oo-upCCD energy is much larger than the energy correction, and so with the same error rate, the former would result in larger absolute errors than the latter. Second, the perturbative energy correction also benefits from the error cancellation, as the errors in the numerator (${Y}_{p}^{2}$) and the denominator (G_p) may cancel with each other. Therefore, the energy correction appears significantly more resilient to errors than the oo-upCCD energy. In Fig. 7 we compare the energy contributions to E⁽²⁾ from unpaired excitations with ${({Y}_{p}/{G}_{p})}^{2}$ above 1 mH, using both the statevector simulator and the Aria QPU. The results from Aria closely align with those of the simulator.

Table 1 Energy contributions of oo-upCCD-PT2 for CH₂OH⁺ between the ideal simulator and the Aria QPU

Fig. 7: Comparison of top energy contributions to $E^{(2)}$ between simulator and quantum hardware.

The plot shows the energy contribution to $E^{(2)}$ from the top 12 unpaired excitations for reaction step 140 of the CH₂OH⁺ decomposition, comparing results from the statevector simulator and the Aria QPU.

In order to improve the absolute energy measurements of oo-upCCD, we take advantage of a simple error mitigation approach based on post-selection. As we have mentioned in section II A, three measurements are needed to measure the energy of the oo-upCCD ansatz: measuring all the qubits in Pauli X, Pauli Y, and Pauli Z basis. The measurements in the Pauli Z basis should only yield binary strings that contains the correct number of electron pairs. For example, consider a 4-qubit, 2-electron pair system: binary strings such as 0011, 1010 are valid, while binary strings like 0111 or 0001 are invalid. On noisy quantum systems, these invalid binary strings could occur due to bit flip errors.

Therefore, in the case of Pauli Z-basis (computational basis) measurements, we retain only those that maintain particle number symmetry and discard the rest. The results are shown in Fig. 6. We find that doing so improves the energy measurements by about 200 mH. We then perform the uniform shift for the post-selected energies by 151 mH. As in the case of CH₂OH⁺ decomposition, the shift is computed as the averaged energy error between the measured results on hardware and the noiseless simulator. After shifting, the results better match the results from the ideal simulator. This demonstrates that the post-selection not only improves absolute energies, but also relative energies.

The experimental results of the CH₃I + Br⁻ S_N2 reaction are shown in Fig. 8 and presented in Table 2. These results are obtained using the IonQ Forte QPU. The S_N2 reaction of CH₃I + Br⁻ is particularly challenging for NISQ quantum systems as the energy differences across the reaction path are small. The energy difference between the transition state and the reactant is about 50 mH, which is a value on the order of the experimental uncertainty. As seen in Fig. 8, the raw energy demonstrates nonphysical behavior. That is, the product energy is even higher than the transition state and the reactant energies. Similar to the CH₂OH⁺ decomposition, the error in the total energy is predominantly due to errors from the unperturbed VQE energy. Therefore, we apply the same Z-basis post-selection, and find that the error mitigated energies now yield the correct behavior, matching well with the predictions of the simulator and CASCI.

Fig. 8: The simulated CH₃I + Br⁻ → CH ₃Br + I⁻ S_N2 reaction energy pathway on the IonQ Forte quantum computer.

The zero of the energy is set to the simulated product state. Data markers are staggered for legibility, and error bars correspond to a statistical error of ± 1 standard error.

Table 2 Energy contributions of oo-upCCD-PT2 for the S_N2 reaction between the ideal simulator and the Forte QPU

Discussion

A common question regarding current NISQ quantum computers is their utility for quantum chemistry, particularly for electronic structure problems. To address this, accurate simulations of these systems are essential. However, when considering the VQE algorithm, it is notable that many proposed VQE approaches, whether based on unitary coupled cluster ansatz or hardware-efficient ansatz^{20,34,35,36,37}, result in circuits that exceed the capabilities of current quantum computers for all but the smallest chemical problems. For this reason, the oo-upCCD ansatz is arguably the most practical VQE variant for execution on contemporary quantum computers for chemical systems. The oo-upCCD ansatz offers three main advantages: first, it needs only half the qubits of many other VQE ansatze; second, the number of two-qubit gates scales quadratically (O(N²)) with system size; and third, the required number of circuits is constant (O(1)), independent of system size. However, its limitation to describing only paired electrons compromises its quantitative accuracy.

Our goal in this study was to explore ways to enhance the precision of the oo-upCCD method while keeping the complexity of the quantum circuit the same (or increasing it in a shallow, controlled manner). Here, we investigated the use of RDM-based second-order perturbation theory. Our findings indicate that this technique can correct most of the errors caused by the electron-pair assumptions of oo-upCCD, especially during the dissociation of multiple bonds in nitrogen (N₂) and lithium oxide (Li₂O) molecules, as well as in calculating the energy barriers and differences between reactants and products in chemical reactions. Trials conducted on IonQ’s trapped-ion quantum computers demonstrate that the energy corrections predicted by PT2 are robust against noise, which can be attributed to the cancellation of errors within the PT2 energy formula. This characteristic suggests that it can be an effective method for use in the current generation of quantum computers.

Despite its advantages, the oo-upCCD-PT2 method faces challenges similar to those found in traditional perturbation theory, including numerical instability and variational collapse. We intend to tackle these challenges in future research. By continuing to refine our methods, in conjunction with hardware improvements, we aim to develop a practical VQE algorithm for near-term devices. This algorithm is intended to solve complex chemical problems with accuracy equal to or surpassing current classical simulation methods. We anticipate that the outcomes of these experiments will offer critical insights into the utility of near-term QPUs for quantum chemistry.

In summary, we have effectively leveraged RDM-based methods to refine the accuracy of the oo-upCCD method through second-order perturbation theory. We demonstrated this through successful applications on both quantum simulators and actual quantum hardware. Motivated by these initial positive results, in future work, we plan to address some of the issues associated with the perturbation theory. A primary issue we observed is the violation of the variational principle, notably during the dissociation of nitrogen (N₂). This limitation may be overcome by implementing measurements within the framework of configuration interaction rather than perturbation theory, potentially leading to an approach similar to the quantum subspace expansion (QSE)^38,39. In addition to QSE, the recently developed non-orthogonal quantum eigensolver (NOQE)⁴⁰ also provides with a useful platform for quantum chemistry simulations beyond VQE, although the Hadamard test used in NOQE will increase the circuit complexity. We plan to explore these and more directions with the goal of landing us on practical quantum advantage for quantum chemistry simulations.

Methods

Trapped-ion quantum computer

The experimental demonstration was performed on the Aria and Forte quantum processing units (QPUs) developed by IonQ. Both QPUs utilize trapped Ytterbium ions where two states in the ground hyperfine manifold are used as qubit states. These states are manipulated by illuminating individual ions with pulses of 355 nm light that drive Raman transitions between the ground states defining the qubit. By configuring these pulses, arbitrary single-qubit gates and Mølmer-Sørenson type two-qubit gates can both be realized. The Forte system⁴¹ contains larger qubit registers and improved gate fidelities than Aria due to the acoustic-optic deflectors that allow independent alignment of each laser beam to each ion. This technique leads to smaller beam alignment error across the chain of trapped ions. Softwares used in this study are described in the Supplementary Information Notes 1.

Derivations of the VQE-PT2 working equations

Here we provide the derivations of the working equations for VQE-PT2. Following Equation (6), plugging the wave function and energy into the time-independent Schrödinger’s equation, and selecting terms up to second order in λ, we obtain

$$\begin{array}{l}{H}_{0}\left\vert {\Psi }^{(0)}\right\rangle ={E}^{(0)}\left\vert {\Psi }^{(0)}\right\rangle \\ {H}_{0}\left\vert {\Psi }^{(1)}\right\rangle +V\left\vert {\Psi }^{(0)}\right\rangle ={E}^{(0)}\left\vert {\Psi }^{(1)}\right\rangle +{E}^{(1)}\left\vert {\Psi }^{(0)}\right\rangle \\ {H}_{0}\left\vert {\Psi }^{(2)}\right\rangle +V\left\vert {\Psi }^{(1)}\right\rangle ={E}^{(0)}\left\vert {\Psi }^{(2)}\right\rangle +{E}^{(1)}\left\vert {\Psi }^{(1)}\right\rangle +{E}^{(2)}\left\vert {\Psi }^{(0)}\right\rangle \\ \end{array}$$

(10)

Next, we constrain $\left\vert {\Psi }^{(1)}\right\rangle$ such that it is orthogonal to $\left\vert {\Psi }^{(0)}\right\rangle$

$$\left\langle {\Psi }^{(1)}| {\Psi }^{(0)}\right\rangle =0.$$

(11)

After left projecting Equation (10) by $\left\langle {\Psi }^{(0)}\right\vert$, we obtain

$$\begin{array}{l}\left\langle {\Psi }^{(0)}| {H}_{0}| {\Psi }^{(0)}\right\rangle ={E}^{(0)}\\ \left\langle {\Psi }^{(0)}| V| {\Psi }^{(0)}\right\rangle ={E}^{(1)}\\ \left\langle {\Psi }^{(0)}| V| {\Psi }^{(1)}\right\rangle ={E}^{(2)}\\ \end{array}$$

(12)

For our reference (zeroth-order) wave function, $\left\vert {\Psi }^{(0)}\right\rangle$, we can use the oo-pUCCD wave function obtained by oo-VQE:

$$\left\vert {\Psi }^{(0)}\right\rangle =\vert{\Psi }_{{\rm{oo-upCCD}}}\rangle$$

(13)

We then partition the second-quantized molecular Hamiltonian as

$$H=\sum _{p}{\epsilon }_{p}{a}_{p}^{\dagger }{a}_{p}+\sum _{pq}{h}_{pq}{a}_{p}^{\dagger }{a}_{q}+\sum _{pqrs}{g}_{pqrs}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}$$

(14)

and we define the zeroth order Hamiltonian as

$${H}_{0}=\sum _{p}{\epsilon }_{p}{a}_{p}^{\dagger }{a}_{p}$$

(15)

in which where p runs over all spin orbitals and ϵ_p are the orbital energies computed by plugging the one body reduced density matrix (1-RDM) of oo-upCCD into the HF orbital energy expression. Similarly, we define the perturbation potential V as

$$V=\sum _{pq}{h}_{pq}{a}_{p}^{\dagger }{a}_{q}+\sum _{pqrs}{g}_{pqrs}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}.$$

(16)

The VQE energy on its own contains both the zeroth and first order energy corrections

$${E}_{{\rm{VQE}}}={E}^{(0)}+{E}^{(1)}.$$

(17)

The leading energy correction beyond the VQE energy enters in the second order

$$\begin{array}{ll}{E}_{{\rm{VQE}}}={E}^{(0)}+{E}^{(1)}\,=\,\left\langle {\Psi }^{(0)}| {H}_{0}| {\Psi }^{(0)}\right\rangle +\left\langle {\Psi }^{(0)}| V| {\Psi }^{(0)}\right\rangle\\\qquad\qquad\qquad\qquad\quad=\,\left\langle {\Psi }^{(0)}| {H}_{0}+V| {\Psi }^{(0)}\right\rangle\\\qquad\qquad\qquad\qquad\quad=\,\left\langle {\Psi }^{(0)}| H| {\Psi }^{(0)}\right\rangle .\end{array}$$

(18)

Let’s now write the first-order wave function correction as

$$\left\vert {\Psi }^{(1)}\right\rangle =\mathop{\sum }\limits_{pqrs}^{{\rm{non-pair}}}{t}_{pqrs}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}\left\vert {\Psi }^{(0)}\right\rangle =\mathop{\sum }\limits_{P}^{{\rm{non-pair}}}{t}_{P}\left\vert {\Psi }_{P}\right\rangle$$

(19)

in which ${a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}$ breaks electron pairs.

In order for ${a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}$ to break electron pairs, we must consider these three scenarios

$$\begin{array}{ll}&{a}_{p\alpha }^{\dagger }{a}_{q\alpha }{a}_{r\alpha }^{\dagger }{a}_{s\alpha }(r\,\ne\,s,p\,\ne\,q,r\,\ne\,q,s\,\ne\,p)(p\, < \,r,q\, < \,s)\\ &{a}_{p\beta }^{\dagger }{a}_{q\beta }{a}_{r\beta }^{\dagger }{a}_{s\beta }(r\,\ne\,s,p\,\ne\,q,r\,\ne\,q,s\,\ne\,p)(p\, < \,r,q\, < \,s)\\ &{a}_{p\alpha }^{\dagger }{a}_{q\alpha }{a}_{r\beta }^{\dagger }{a}_{s\beta }(r\,\ne\,s,p\,\ne\,q,p\,\ne\,r| | q\,\ne\,s)\\ \end{array}$$

(20)

in which the first parenthesis enforces broken-pairing, and the second parenthesis ensures no double counting.

The second-order energy correction becomes

$${E}^{(2)}=\mathop{\sum }\limits_{P}^{{\rm{non-pair}}}{t}_{P}\left\langle {\Psi }^{(0)}| V| {\Psi }_{P}\right\rangle$$

(21)

in which we need to compute t_P.

Left projecting Equation (10) by $\left\vert {\Psi }_{Q}\right\rangle$, we obtain

$$\sum _{P}{t}_{P}\left\langle {\Psi }_{Q}| {H}_{0}| {\Psi }_{P}\right\rangle +\left\langle {\Psi }_{Q}| V| {\Psi }^{(0)}\right\rangle ={E}^{(0)}\sum _{P}{t}_{P}\left\langle {\Psi }_{Q}| {\Psi }_{P}\right\rangle$$

(22)

where both P and Q denote non-pair excitations. Rearranging the above equation gives:

$$\begin{array}{ll}&\mathop{\sum}\limits_{P}{t}_{P}\left(\left\langle {\Psi }_{Q}| {H}_{0}| {\Psi }_{P}\right\rangle -{E}^{(0)}\left\langle {\Psi }_{Q}| {\Psi }_{P}\right\rangle \right)=-\left\langle {\Psi }_{Q}| V| {\Psi }^{(0)}\right\rangle \\ &\mathop{\sum}\limits_{P}{G}_{PQ}{t}_{P}=-{Y}_{Q}\end{array}$$

(23)

where we define

$$\begin{array}{ll}&{G}_{PQ}=\left\langle {\Psi }_{Q}| {H}_{0}| {\Psi }_{P}\right\rangle -{E}^{(0)}\left\langle {\Psi }_{Q}| {\Psi }_{P}\right\rangle \\ &{Y}_{P}=\left\langle {\Psi }_{P}| V| {\Psi }^{(0)}\right\rangle \end{array}$$

(24)

so we can then solve $\overrightarrow{t}$ by

$$\overrightarrow{t}=-{{\bf{G}}}^{-1}\overrightarrow{Y}.$$

(25)

We then plug $\overrightarrow{t}$ into Eq. (21) to compute E⁽²⁾. Finally, the total energy is

$$E={E}_{{\rm{VQE}}}+{E}^{(2)}$$

(26)

Now we need to compute the G matrix and the $\overrightarrow{Y}$ vector. Elements of the G matrix take the form

$$\begin{array}{ll}{G}_{PQ}\,=\,\mathop{\sum}\limits_{k}{\epsilon }_{k}\langle {\Psi }^{(0)}| {a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{k}^{\dagger }{a}_{k}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}| {\Psi }^{(0)}\rangle \\\qquad\;\;-\,{E}^{(0)}\langle{\Psi }^{(0)}| {a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}| {\Psi }^{(0)}\rangle \end{array}$$

(27)

We approximate G with its diagonal elements

$$\begin{array}{ll}{G}_{PP}\,=\,\mathop{\sum}\limits_{k}{\epsilon }_{k}\langle{\Psi }^{(0)}| {a}_{s}^{\dagger }{a}_{r}{a}_{q}^{\dagger }{a}_{p}{a}_{k}^{\dagger }{a}_{k}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}| {\Psi }^{(0)}\rangle\\\qquad\;\;-\,{E}^{(0)}\langle{\Psi }^{(0)}| {a}_{s}^{\dagger }{a}_{r}{a}_{q}^{\dagger }{a}_{p}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}| {\Psi }^{(0)}\rangle\\\qquad\;\;=\,{\sum}_{k}{\epsilon }_{k}{\Gamma }_{sqkpr}^{rpkqs}-{E}^{(0)}{\Gamma }_{sqpr}^{rpqs}\end{array}$$

(28)

in which we have defined the 5-particle reduced density matrix (5-RDM). Here one needs to note that the diagonal approximation of G is made mainly for efficiency reasons, and similar approximations have been made in other seniority-zero based perturbation theories^42,43. As $\left\vert {\Psi }^{(0)}\right\rangle$ deviates more from a single determinant, the sizes of the off-diagonal elements in G become larger, and the diagonal approximation could lead to errors in the computed energy corrections. More studies are needed to understand the effect of such a diagonal approximation to energy corrections, and we wish to address it in future research.

We also need to compute the $\overrightarrow{Y}$ vector as

$$\begin{array}{ll}{Y}_{P}\,=\,\mathop{\sum}\limits_{pq}{h}_{pq}\langle{\Psi }^{(0)}| {a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{p}^{\dagger }{a}_{q}| {\Psi }^{(0)}\rangle\\\qquad+\,{\sum}_{pqrs}{g}_{pqrs}\langle{\Psi }^{(0)}| {a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}| {\Psi }^{(0)}\rangle\\ \qquad=\,{\sum}_{pq}{h}_{pq}{\Gamma }_{uxp}^{vyq}+\sum _{pqrs}{g}_{pqrs}{\Gamma }_{uxpr}^{vyqs}\\\end{array}$$

(29)

in which we need 3- and 4-RDMs. h and g are the one- and two-electron integrals, respectively.

The most computationally-intensive step of the VQE-PT2 approach is in the computation of the 4-RDMs from Equation (29), which contains eight different indices. A naive way of enumerating all those indices would then scale as O(N⁸). However, although the term ${a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}\left\vert {\Psi }^{(0)}\right\rangle$ in the first-order wave function correction contains broken-pair configurations, all electrons should still be paired in ${a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}\left\vert {\Psi }^{(0)}\right\rangle$. Otherwise the overlap with $\left\vert {\Psi }^{(0)}\right\rangle$ becomes zero. Therefore, only four indices out of the original eight are unique, and by carefully picking out the non-zero terms allows us to reduce the cost to O(N⁴). To be more specifically, the operator ${a}_{u}^{\dagger }{a}_{v}{a}_{x}^{\dagger }{a}_{y}{a}_{p}^{\dagger }{a}_{q}{a}_{r}^{\dagger }{a}_{s}$ must be written in terms of

• number operators ${n}_{p}={a}_{p}^{\dagger }{a}_{p}\to \frac{1}{2}(1-{Z}_{p})$

• double creation operators ${d}_{p}^{\dagger }={a}_{p\alpha }^{\dagger }{a}_{p\beta }^{\dagger }\to \frac{1}{2}({X}_{p}-i{Y}_{p})$

• double annihilation operators ${d}_{p}={a}_{p\beta }{a}_{p\alpha }\to \frac{1}{2}({X}_{p}+i{Y}_{p})$

in which the expression at the right of the arrow is the Jordan-Wigner transformed formalism of these operators.

Therefore, for 4-RDMs, one only needs to measure a subset of rank-4 Pauli strings that includes: (1) Pauli strings with four Pauli-Z matrices, (2) Pauli strings with two Pauli-Z matrices and two Pauli-X matrices, (3) Pauli strings with two Pauli-Z matrices and two Pauli-Y matrices, (4) Pauli strings with two Pauli-X matrices and two Pauli-Y matrices. The rest of the Pauli strings do not contribute as a result of symmetry violation. We then group this Pauli strings and find terms that are qubitwise commutative⁴⁴ with each other, and measure them altogether. The readers could refer to Supplementary Information Notes 2–5 for more detailed descriptions of how to construct and post-process the 4-RDMs efficiently.