Group-theoretic error mitigation enabled by classical shadows and symmetries

Abstract

Estimating expectation values is a key subroutine in quantum algorithms. Near-term implementations face two major challenges: a limited number of samples required to learn a large collection of observables, and the accumulation of errors in devices without quantum error correction. To address these challenges simultaneously, we develop a quantum error-mitigation strategy called symmetry-adjusted classical shadows, by adjusting classical-shadow tomography according to how symmetries are corrupted by device errors. As a concrete example, we highlight global U(1) symmetry, which manifests in fermions as particle number and in spins as total magnetization, and illustrate their group-theoretic unification with respective classical-shadow protocols. We establish rigorous sampling bounds under readout errors obeying minimal assumptions, and perform numerical experiments with a more comprehensive model of gate-level errors derived from existing quantum processors. Our results reveal symmetry-adjusted classical shadows as a low-cost strategy to mitigate errors from noisy quantum experiments in the ubiquitous presence of symmetry.

Introduction

Quantum computers are highly susceptible to errors at the hardware level, posing a considerable challenge to realize meaningful applications in the so-called noisy intermediate-scale quantum (NISQ) era^1,2. One particularly promising and natural candidate for NISQ applications is the simulation of quantum many-body physics and chemistry^3,4,5,6. In order to minimize the accumulation of errors, such algorithms prioritize low-depth circuits, for instance, variational quantum circuits^7,8,9,10. However, in order to exhibit quantum advantage, these circuits must also be beyond the capabilities of classical simulation^11,12,13,14, resulting in noise levels that nonetheless corrupt the calculations.

While quantum error correction is the long-term solution, current state-of-the-art hardware is still a few orders of magnitude from achieving scalable, fault-tolerant quantum computation^{15,16,17,18,19,20,21,22,23}. In the meantime, there have been considerable theoretical and experimental efforts probing the beyond-classical potential of NISQ computers^{24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46}. Should such an application be demonstrated, quantum error mitigation (QEM) is expected to play a crucial role. Broadly speaking, QEM aims to approximately recover the output of an ideal quantum computation, given only access to noisy quantum devices and offline classical resources. We refer the reader to refs. ^47,48 for a review of prominent concepts and strategies in QEM.

A related but separate challenge for NISQ algorithms is the need to learn many observables in a rudimentary fashion, i.e., by repeatedly running and sampling from quantum circuits. The number of repetitions required can be immense, both to suppress shot noise and to handle the measurement of noncommuting observables^49,50. One particularly promising approach is that of classical shadows^51,52. In contrast to prior measurement strategies^10,53,54,55, classical shadows are remarkably simple to implement and have been shown to exhibit optimal sample complexity in certain important scenarios^51,56.

Classical shadows were developed primarily from the union of two themes in quantum learning theory: linear-inversion estimators for state tomography^57,58 (closed-form solutions that admit fast postprocessing and rigorous guarantees) and the framework of shadow tomography^59,60 (predict only a subset of observables, not the entire density matrix). The result is a simple but powerful protocol that accurately estimates a large collection of observables from relatively few samples. In terms of quantum resources, classical shadows only require the ability to measure in randomly selected bases, making the protocol particularly amenable to NISQ constraints. These desirable features have inspired a wide range of extensions and applications, for example: entanglement detection⁶¹, quantum Fisher information bounds^62,63, learning quantum processes^64,65, navigating variational landscapes^66,67, energy-gap estimation⁶⁸, and applications to fermions^{69,70,71,72,73,74} and bosons^75,76. For an overview of classical shadows and randomized measurement strategies, see ref. ⁷⁷.

Due to their experimental friendliness and versatile prediction power, classical shadows naturally have been considered for QEM as well. For example, refs. ^78,79 used classical shadows to approximately project a noisy quantum state toward a target subspace via classical postprocessing, the subspaces being either the logical subspace of an error-correcting code⁸⁰ and/or the dominant eigenvector (purification) of the noisy mixed state^81,82. These shadow-based ideas circumvent some of the difficulties of performing subspace projection, at the cost of an exponential sample complexity. Meanwhile, ref. ⁸³ intertwined classical shadows with other popular QEM strategies, with a particular focus on probabilistic error cancellation⁸⁴. They establish rigorous estimators and performance guarantees, assuming an accurate characterization of the noisy quantum device. Finally, refs. ^85,86 described modifications to the classical linear-inversion step in order to mitigate errors in the randomized measurements. In particular, robust shadow estimation⁸⁵ assumes no prior knowledge of the noise, instead implementing a separate calibration experiment that learns the necessary noise features.

In this paper, we take this latter perspective^85,86, with an eye on a more comprehensive mitigation of errors beyond readout errors. We introduce a QEM protocol, which we refer to as symmetry-adjusted classical shadows, that takes advantage of known symmetries in the quantum system of interest. For example, in simulations of chemistry, the number of electrons is typically fixed. The corruption of such symmetries by noise informs us how to undo the effects of that noise. Crucially, because randomized measurements scramble the information, the other properties of the quantum system are corrupted (and therefore can be mitigated) in the same manner. Using these insights, symmetry-adjusted classical shadows appropriately modifies the linear-inversion based on the symmetry information alone.

A notable advantage of our protocol is that we do not run any extraneous calibration experiments. This has the added benefit of inherently accounting for errors that occur throughout the full quantum circuit, rather than the randomized measurements in isolation^{85,86,87,88,89}. Also, the simplicity of the protocol allows for additional QEM techniques to be straightforwardly applied in tandem. Finally, in contrast to other symmetry-based ideas^83,90,91,92, our approach goes beyond the concept of symmetry projection, instead utilizing a unified group-theoretic understanding of classical shadows in conjunction with symmetries. We expound on this distinction in the Supplementary Discussion, wherein we review these prior symmetry-based QEM techniques.

This paper is structured as follows. In the Results section, we begin by establishing preliminaries and background material. We then introduce our main contribution, symmetry-adjusted classical shadows, and describe its key application for mitigating local fermionic and qubit observables. We follow by highlighting additional technical results: a modification to random Pauli measurements required to tailor its irreps for use with common symmetries, called subsystem-symmetrized Pauli shadows; an improved design for compiling fermionic Gaussian unitaries with lower circuit depth and fewer gates than prior art; and a symmetry adaptation to fermionic classical shadows which reduces the quantum resources required, applicable to fermionic systems with spin symmetry. Finally, we close the Results section with a series of numerical experiments, demonstrating the effectiveness of our error-mitigation protocol under realistic scenarios. This includes simulations of a noise model based on existing superconducting-qubit platforms⁹³. In the Discussion section, we summarize our findings and discuss future prospects. In the Methods section, we illustrate the general theory of symmetry-adjusted classical shadows, and we provide further technical details regarding the applications to fermion and qubit systems with global U(1) symmetries. Details regarding the mathematical proofs and numerical simulations are provided in the Supplementary Information, and code for the latter is available at our open-source repository (https://github.com/zhao-andrew/symmetry-adjusted-classical-shadows).

Results

Background

First, we provide a review of classical shadows^51,52 and robust shadow estimation⁸⁵ necessary to understand our technical results. Readers familiar with this background material can skip to the subsection “Symmetry-adjusted classical shadows,” after familiarizing themselves with the notation that we establish below.

Notation and preliminaries

For any integer N > 1, we define [N]: = {0, …, N − 1} (note that we index starting from 0). We use ${{{\rm{i}}}}\equiv \sqrt{-1}$ for the imaginary unit.

Throughout this paper, we consider an n-qubit system with Hilbert space ${{{\mathcal{H}}}}:={({{\mathbb{C}}}^{2})}^{\otimes n}$. Its dimension is denoted by d ≡ 2ⁿ unless otherwise specified. We often work with the space of linear operators ${{{\mathcal{L}}}}({{{\mathcal{H}}}})\cong {{\mathbb{C}}}^{d\times d}$ as a vector space, so it will be convenient to employ the Liouville representation: for any operator $A\in {{{\mathcal{L}}}}({{{\mathcal{H}}}})$, its vectorization $\left.\left\vert A\right\rangle \!\right\rangle \in {{\mathbb{C}}}^{{d}^{2}}$ in some orthonormal operator basis $\{{B}_{1},\ldots ,{B}_{{d}^{2}}: {{{\rm{tr}}}}({B}_{i}^{{\dagger} }{B}_{j})={\delta }_{ij}\}$ is defined by the components $\langle \!\langle {B}_{i}| A\rangle \!\rangle :={{{\rm{tr}}}}({B}_{i}^{{\dagger} }A)$. Under this representation, superoperators are mapped to d² × d² matrices: any ${{{\mathcal{E}}}}\in {{{\mathcal{L}}}}({{{\mathcal{L}}}}({{{\mathcal{H}}}}))$ can be specified by its matrix elements ${{{{\mathcal{E}}}}}_{ij}:=\langle \!\langle {B}_{i}| {{{\mathcal{E}}}}| {B}_{j}\rangle \!\rangle ={{{\rm{tr}}}}({B}_{i}^{{\dagger} }{{{\mathcal{E}}}}({B}_{j}))$. We let ${{{\mathcal{E}}}}$ denote both the superoperator and its matrix representation, and in a similar fashion we sometimes write $\left.\left\vert A\right\rangle \!\right\rangle =A$.

For systems of qubits, the normalized Pauli operators ${{{\mathcal{P}}}}(n)/\sqrt{d}$ are a convenient basis for ${{{\mathcal{L}}}}({{{\mathcal{H}}}})$, where

$${{{\mathcal{P}}}}(n):={\{{\mathbb{I}},X,Y,Z\}}^{\otimes n}.$$

(1)

This choice is called the Pauli transfer matrix (PTM) representation. The weight, or locality, of a Pauli operator $P\in {{{\mathcal{P}}}}(n)$ is the number of its nontrivial tensor factors, denoted by ∣P∣. For each i ∈ [n], we define ${W}_{i}\in {{{\mathcal{P}}}}(n)$ which acts as W ∈ {X, Y, Z} on the ith qubit and trivially on the rest of the system.

For fermions in second quantization, a natural choice of basis is the set of Majorana operators, defined as $\{{\Gamma }_{{{{\boldsymbol{\mu }}}}}/\sqrt{d}: {{{\boldsymbol{\mu }}}}\subseteq [2n]\}$ where

$${\Gamma }_{{{{\boldsymbol{\mu }}}}}:={(-{{{\rm{i}}}})}^{{| {{{\boldsymbol{\mu }}}}|}\choose{2}}\mathop{\prod}\limits_{\mu \in {{{\boldsymbol{\mu }}}}}{\gamma }_{\mu }.$$

(2)

The Hermitian generators $\{{\gamma }_{\mu }: \mu \in [2n]\}\subset {{{\mathcal{L}}}}({{{\mathcal{H}}}})$ obey the anticommutation relation ${\gamma }_{\mu }{\gamma }_{\nu }+{\gamma }_{\nu }{\gamma }_{\mu }=2{\delta }_{\mu \nu }{\mathbb{I}}$ (we will use ${\mathbb{I}}$ to denote any identity operator whose dimension is clear from context). They are related to the fermionic creation and annihilation operators ${a}_{p}^{{\dagger} },{a}_{p}$ via

$${\gamma }_{2p}={a}_{p}+{a}_{p}^{{\dagger} },\quad {\gamma }_{2p+1}=-{{{\rm{i}}}}({a}_{p}-{a}_{p}^{{\dagger} }).$$

(3)

By convention, the elements of μ and the product in Eq. (2) are in strictly ascending order. We call ∣μ∣ the degree of Γ_μ, or equivalently refer to them as (∣μ∣/2)-body operators whenever the degree is even. It is straightforward to check that Majorana operators are isomorphic to Pauli operators, in particular satisfying the orthogonality relation 〈〈Γ_μ∣Γ_ν〉〉 = dδ_μν.

For any unitary U ∈ U(d), its corresponding channel is denoted by ${{{\mathcal{U}}}}(\cdot ):=U(\cdot ){U}^{{\dagger} }$. For any $\left\vert \varphi \right\rangle \in {{{\mathcal{H}}}}$, $\left.\left\vert \varphi \right\rangle \!\right\rangle$ is the vectorization of $\vert \varphi \rangle \!\langle \varphi\vert$. We use tildes to indicate objects affected by quantum noise, e.g., $\widetilde{{{{\mathcal{U}}}}}$ denotes a noisy implementation of the ${{{\mathcal{U}}}}$. Hats indicate statistical estimators, e.g., $\hat{o}$ denotes an estimate for $o={{{\rm{tr}}}}(O\rho )$. Asymptotic upper and lower bounds are denoted by ${{{\mathcal{O}}}}(\cdot )$ and Ω( ⋅ ) respectively, and f(x) = Θ(g(x)) means that f(x) is both ${{{\mathcal{O}}}}(g(x))$ and Ω(g(x)).

Classical shadows

We summarize the method of classical shadows as formalized by Huang et al.⁵¹, borrowing the PTM language of Chen et al.⁸⁵ which will make the robust extension clear later. Our task is to estimate the expectation values ${{{\rm{tr}}}}({O}_{j}\rho )=\langle \!\langle {O}_{j}| \rho \rangle \!\rangle$ of a collection of L observables ${O}_{1},\ldots ,{O}_{L}\in {{{\mathcal{L}}}}({{{\mathcal{H}}}})$, ideally using as few copies of ρ as possible. Classical shadows is based on a simple measurement primitive: for each copy of ρ, apply a unitary U randomly drawn from a distribution of unitaries and measure in the computational basis. This produces a sample b ∈ {0, 1}ⁿ with probability $\langle \!\langle b| {{{\mathcal{U}}}}| \rho \rangle \!\rangle$. One then inverts the unitary on the outcome $\left\vert b\right\rangle$ in postprocessing, which amounts to storing a classical representation of ${U}^{{\dagger} }\left\vert b\right\rangle$.

The unitary distribution determines the efficiency of this protocol with respect to the properties of interest. Throughout this paper, we assume that the distribution is a finite group equipped with the uniform probability distribution (it is straightforward to generalize to compact groups, using their Haar measures). Specifically, let $U:G\to {{{\rm{U}}}}({{{\mathcal{H}}}})$ be a unitary representation of a group G. The measurement primitives averaged over all random unitaries and measurement outcomes implement the quantum channel

$${{{\mathcal{M}}}}:=\mathop{\mathbb{E}}\limits_{g \sim G}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }{{{{\mathcal{M}}}}}_{Z}{{{{\mathcal{U}}}}}_{g}\equiv \frac{1}{| G| }\mathop{\sum}\limits_{g\in G}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }{{{{\mathcal{M}}}}}_{Z}{{{{\mathcal{U}}}}}_{g},$$

(4)

where

$${{\mathcal{M}}_z}=\mathop{\sum}\limits_{b\in \{0,1\}^n}| b \rangle\rangle\langle\langle b |$$

(5)

describes the effective process of computational-basis measurements. The channel ${{{{\mathcal{U}}}}}_{g}$ is the random unitary acting on the target state ρ, while ${{{{\mathcal{U}}}}}_{g}^{{\dagger} }$ is its classically computed inversion on the measurement outcomes $\left.\left\vert b\right\rangle \!\right\rangle$. Thus in expectation we produce the state

$${{{\mathcal{M}}}}\left.\left\vert \rho \right\rangle \!\right\rangle =\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\vert \rho \rangle \!\rangle }{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\vert b \rangle \!\rangle.$$

(6)

If ${{{\mathcal{M}}}}$ is invertible (corresponding to informational completeness of the measurement primitive), then applying ${{{{\mathcal{M}}}}}^{-1}$ to Eq. (6) recovers the state:

$$\left.\left\vert \rho \right\rangle \!\right\rangle ={{{{\mathcal{M}}}}}^{-1}{{{\mathcal{M}}}}\left.\left\vert \rho \right\rangle \!\right\rangle =\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\vert \rho \rangle \!\rangle }{{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\left.\left\vert b\right\rangle \!\right\rangle .$$

(7)

The objects $\vert {\hat{\rho }}_{g,b}\rangle \!\rangle :={{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\vert b\rangle \!\rangle$ are called the classical shadows of $\left.\left\vert \rho \right\rangle \!\right\rangle$, for which they serve as unbiased estimators. Hence by construction they can predict expectation values,

$$\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\vert \rho \rangle \!\rangle }\langle \!\langle {O}_{j}| {\hat{\rho }}_{g,b}\rangle \!\rangle =\langle \!\langle {O}_{j}| \rho \rangle \!\rangle ,$$

(8)

as well as nonlinear functions of ρ⁵¹. While ${{{{\mathcal{M}}}}}^{-1}$ is not a physical map (it is not completely positive), it only appears as classical postprocessing. Such a computation can be accomplished, for instance, by first deriving a closed-form expression for ${{{\mathcal{M}}}}$.

One systematic approach to deriving such an expression is through the representation theory of G. First, note that the d-dimensional unitary U is promoted to a d²-dimensional representation ${{{\mathcal{U}}}}$. Equation (4) reveals that ${{{\mathcal{M}}}}$ is a twirl of ${{{{\mathcal{M}}}}}_{Z}$ by the group G under the action of ${{{\mathcal{U}}}}$. Such objects are well studied: assuming that the irreducible components of ${{{\mathcal{U}}}}$ have no multiplicities, an application of Schur’s lemma implies that⁹⁴

$${{{\mathcal{M}}}}=\mathop{\sum}\limits_{\lambda \in {R}_{G}}{f}_{\lambda }{\Pi }_{\lambda }.$$

(9)

Note that the general expression with multiplicities can be found in [ref. ⁸⁵, Eq. (A6)]. Here, R_G is the set of labels λ for the irreducible representations (irreps) of G. The superoperators Π_λ are orthogonal projectors onto the irreducible subspaces ${V}_{\lambda }\subseteq {{{\mathcal{L}}}}({{{\mathcal{H}}}})$. Choosing an orthonormal basis $\{\vert {B}_{\lambda }^{j}\rangle \!\rangle : j=1,\ldots ,\dim {V}_{\lambda }\}$ for each subspace, we can write the projectors as

$${{\Pi }_{\lambda }=\mathop{\sum}\limits_{j=1}^{\dim {V}_{\lambda }}\vert {B}_{\lambda }^{j}\Big\rangle \!\Big\rangle \Big\langle \!\Big\langle {B}_{\lambda }^{j}\vert}.$$

(10)

The eigenvalues f_λ of ${{{\mathcal{M}}}}$ can be computed using the orthogonality of projectors:

$${f}_{\lambda }=\frac{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })}{{{{\rm{tr}}}}({\Pi }_{\lambda })}.$$

(11)

Note that ${{{\rm{tr}}}}({\Pi }_{\lambda })=\dim {V}_{\lambda }$. From this diagonalization, we immediately acquire an expression for the desired inverse:

$${{{{\mathcal{M}}}}}^{-1}=\mathop{\sum}\limits_{\lambda \in {R}_{G}}{f}_{\lambda }^{-1}{\Pi }_{\lambda }.$$

(12)

If some f_λ = 0, then we may instead define ${{{{\mathcal{M}}}}}^{-1}$ as the pseudoinverse on the subspaces where f_λ is nonvanishing. This implies that the measurement primitive is informationally complete only within those subspaces.

To analyze the sample efficiency of this protocol, suppose we have performed T experiments, yielding a collection of independent classical shadows ${\hat{\rho }}_{1},\ldots ,{\hat{\rho }}_{T}$ where each $\left.\left\vert {\hat{\rho }}_{\ell }\right\rangle \!\right\rangle ={{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{{g}_{\ell }}^{{\dagger} }\left.\left\vert {b}_{\ell }\right\rangle \!\right\rangle$. From this data we can construct estimates

$${\hat{o}}_{j}(T)=\frac{1}{T}\mathop{\sum }\limits_{\ell =1}^{T}\langle \!\langle {O}_{j}| {\hat{\rho }}_{\ell }\rangle \!\rangle ,$$

(13)

which by linearity converge to ${{{\rm{tr}}}}({O}_{j}\rho )$. The single-shot variance of ${\hat{o}}_{j}$ can be bounded in terms of the so-called shadow norm:

$$\begin{array}{ll}{{{\rm{Var}}}}[{\hat{o}}_{j}]\,\le \,\mathop{\rm{max}}\limits_{{{{\rm{states}}}}\,\sigma }\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\left.\left\vert \sigma \right\rangle \!\right\rangle }{\langle \!\langle {O}_{j}| {{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }| b\rangle \!\rangle }^{2}\\ \qquad\quad\,\,=:\,\Vert {O}_{j}{\Vert }_{{{{\rm{shadow}}}}}^{2}.\end{array}$$

(14)

This variance controls the prediction error, rigorously established via probability tail bounds. In particular, taking a number of samples

$$T={{{\mathcal{O}}}}\left(\frac{\log (L/\delta )}{{\epsilon }^{2}}\mathop{\rm{max}}\limits_{1\le j\le L}{\parallel} {O}_{j}{\parallel }_{{{{\rm{shadow}}}}}^{2}\right)$$

(15)

ensures that, with probability at least 1 − δ, each estimate exhibits at most ϵ additive error:

$$| {\hat{o}}_{j}(T)-\langle \!\langle {O}_{j}| \rho \rangle \!\rangle | \le \epsilon .$$

(16)

Note that for simplicity we employ the mean estimator throughout this paper, which suffices whenever the ensemble is either local Cliffords or matchgates and the observables are Pauli or Majorana operators [ref. ⁶⁹, Supplemental Material, Theorem 12]. In general, a median-of-means estimator can guarantee the advertised sample complexity regardless of ensemble.

Finally, we comment on the classical computation of ${\hat{o}}_{j}$. In order to evaluate Eq. (13), one may use Eqs. (10) and (12) to express the ℓth-sample estimate as

$$\langle \!\langle {O}_{j}| {\hat{\rho }}_{\ell }\rangle \!\rangle =\mathop{\sum}\limits_{\lambda \in {R}_{G}}{f}_{\lambda }^{-1}\mathop{\sum }\limits_{k=1}^{\dim {V}_{\lambda }}\Big\langle \!\Big\langle {O}_{j}\Big\vert {B}_{\lambda }^{k}\Big\rangle \!\Big\rangle \Big\langle \!\Big\langle {B}_{\lambda }^{k}\Big\vert {{{{\mathcal{U}}}}}_{{g}_{\ell }}^{{\dagger} }\Big\vert {b}_{\ell }\Big\rangle \!\Big\rangle .$$

(17)

Thus it suffices to be able to efficiently compute the expansion coefficients $\langle \!\langle {O}_{j}| {B}_{\lambda }^{k}\rangle \!\rangle ={{{\rm{tr}}}}({O}_{j}{B}_{\lambda }^{k})$ of the observable O_j in a basis of V_λ, as well as the matrix elements $\langle \!\langle {B}_{\lambda }^{k}| {{{{\mathcal{U}}}}}_{g}^{{\dagger} }| b\rangle \!\rangle =\langle b| {U}_{g}{({B}_{\lambda }^{k})}^{{\dagger} }{U}_{g}^{{\dagger} }| b\rangle$. Note that this does not require explicitly representing the classical shadow ${{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\left.\left\vert b\right\rangle \!\right\rangle$; we only need to determine the diagonal entry of the rotated operator ${U}_{g}{({B}_{\lambda }^{k})}^{{\dagger} }{U}_{g}^{{\dagger} }$ for a given basis state $\left\vert b\right\rangle$.

Robust shadow estimation

We now summarize the robust shadow estimation protocol by Chen et al.⁸⁵; we note that refs. ^87,88,89 describe analogous ideas in the case of random single-qubit measurements. The basic premise is the fact that Schur’s lemma applies to the twirl of any channel, not just ${{{{\mathcal{M}}}}}_{Z}$. Suppose that instead of ${{{{\mathcal{U}}}}}_{g}$, the quantum computer implements a noisy channel ${\widetilde{{{{\mathcal{U}}}}}}_{g}$ which obeys the following assumptions:

Assumptions 1

([ref. ⁸⁵, Simplifying noise assumption A1]). The noise in ${\widetilde{{{{\mathcal{U}}}}}}_{g}$ is gate independent, time stationary, and Markovian. Hence there exists the decomposition ${\widetilde{{{{\mathcal{U}}}}}}_{g}={{{\mathcal{E}}}}{{{{\mathcal{U}}}}}_{g}$, where ${{{\mathcal{E}}}}$ is a completely positive, trace-preserving map, independent of both the ideal unitary and the experimental time.

They also assume the ability to prepare the state $\left\vert {0}^{n}\right\rangle$ with sufficiently high fidelity. Given these conditions, the noisy version of the shadow channel implemented in experiment becomes

$$\widetilde{{{{\mathcal{M}}}}}:=\mathop{\mathbb{E}}\limits_{g \sim G}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }{{{{\mathcal{M}}}}}_{Z}{\widetilde{{{{\mathcal{U}}}}}}_{g}=\frac{1}{| G| }\mathop{\sum}\limits_{g\in G}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }{{{{\mathcal{M}}}}}_{Z}{{{\mathcal{E}}}}{{{{\mathcal{U}}}}}_{g},$$

(18)

which is now a twirl over the composite channel ${{{{\mathcal{M}}}}}_{Z}{{{\mathcal{E}}}}$. Although ${{{\mathcal{E}}}}$ is unknown, Schur’s lemma implies that the eigenbasis is preserved, as we now have

$$\widetilde{{{{\mathcal{M}}}}}=\mathop{\sum}\limits_{\lambda \in {R}_{G}}{\widetilde{f}}_{\lambda }{\Pi }_{\lambda },$$

(19)

where the eigenvalues depend on ${{{\mathcal{E}}}}$,

$${\widetilde{f}}_{\lambda }=\frac{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{{{\mathcal{E}}}}{\Pi }_{\lambda })}{{{{\rm{tr}}}}({\Pi }_{\lambda })}.$$

(20)

Therefore if one knows ${\widetilde{f}}_{\lambda }$, then one can perform the correct linear inversion in the presence of noise, i.e., by replacing ${f}_{\lambda }^{-1}$ with ${\widetilde{f}}_{\lambda }^{-1}$ in Eq. (17).

Because ${{{\mathcal{E}}}}$ depends on the details of the quantum hardware, it is not possible to determine ${\widetilde{f}}_{\lambda }$ without an a priori accurate characterization of the noise. Absent such information, a calibration protocol is proposed to experimentally estimate the value of ${\widetilde{f}}_{\lambda }$. This proceeds by performing the classical shadows protocol on a fiducial state $\left\vert {0}^{n}\right\rangle$, rather than the unknown target state ρ. This enables the study of errors in the random circuits U_g. Because $\left\vert {0}^{n}\right\rangle$ is known exactly, one can compare its noiseless properties against the noisy experimental data to determine a calibration factor.

Specifically, Chen et al.⁸⁵ construct an estimator NoiseEst_G(λ, g, b) for each sample (U_g, b) of the calibration experiment, which converges to ${\widetilde{f}}_{\lambda }$ in expectation over g and b. Although they do not prescribe a generic expression for NoiseEst_G (instead considering particular choices of G), it is straightforward to derive one following their ideas. Let D_λ ∈ V_λ be an observable supported exclusively by a single irrep such that 〈0ⁿ∣D_λ∣0ⁿ〉 ≠ 0. Then we have

$$\langle \!\langle {D}_{\lambda }| \widetilde{{{{\mathcal{M}}}}}| {0}^{n}\rangle \!\rangle ={\widetilde{f}}_{\lambda }\langle {0}^{n}| {D}_{\lambda }| {0}^{n}\rangle .$$

(21)

On the other hand, using the fact that

$$\begin{array}{lll}\langle \!\langle {D}_{\lambda }| \widetilde{{{{\mathcal{M}}}}}| {0}^{n}\rangle \!\rangle \,=\,\langle \!\langle {D}_{\lambda }\vert \mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\vert {0}^{n}\rangle \!\rangle }{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\vert b\rangle \!\rangle \\ \qquad\qquad\qquad=\,\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {{{{\mathcal{U}}}}}_{g}\left.\left\vert {0}^{n}\right\rangle \!\right\rangle }\langle b| {U}_{g}{D}_{\lambda }{U}_{g}^{{\dagger} }| b\rangle ,\end{array}$$

(22)

it follows that the random variable

$${{{{\rm{NoiseEst}}}}}_{G}(\lambda ,g,b)=\frac{\langle b| {U}_{g}{D}_{\lambda }{U}_{g}^{{\dagger} }| b\rangle }{\langle {0}^{n}| {D}_{\lambda }| {0}^{n}\rangle }$$

(23)

obeys ${{\mathbb{E}}}_{g,b}\left[{{{{\rm{NoiseEst}}}}}_{G}(\lambda ,g,b)\right]={\widetilde{f}}_{\lambda }$.

One can recover the definitions for NoiseEst_G introduced by Chen et al.⁸⁵ as follows. The global Clifford group Cl(n) has two irreps: the span of the identity operator, ${V}_{0}={{{\rm{span}}}}\{{\mathbb{I}}\}$ (which is trivial), and its orthogonal complement ${V}_{1}={V}_{0}^{\perp }$ (the set of all traceless operators). Choosing ${D}_{1}=d\left\vert {0}^{n}\right\rangle \left\langle {0}^{n}\right\vert -{\mathbb{I}}$ gives

$${{{{\rm{NoiseEst}}}}}_{{{{\rm{Cl}}}}(n)}(1,U,b)=\frac{d| \langle b| U| {0}^{n}\rangle {| }^{2}-1}{d-1},$$

(24)

where U ∈ Cl(n).

On the other hand, the local Clifford group Cl(1)^⊗n has 2ⁿ irreps, labeled by all subsets I ⊆ [n]. Each I indexes a subsystem of qubits, and each subspace V_I is the span of all n-qubit Pauli operators which act nontrivially on exactly that subsystem. Defining

$${D}_{I}:=\mathop{\prod}\limits_{i\in I}{Z}_{i},$$

(25)

one obtains

$$\begin{array}{lll}{{{{\rm{NoiseEst}}}}}_{{{{\rm{Cl}}}}{(1)}^{\otimes n}}(I,U,b)\,=\,\displaystyle{\frac{\langle b| U{D}_{I}{U}^{{\dagger} }| b\rangle }{\langle {0}^{n}| {D}_{I}| {0}^{n}\rangle }}\\ \qquad\qquad\qquad\qquad\qquad\,=\,\mathop{\prod}\limits_{i\in I}\langle {b}_{i}| {C}_{i}Z{C}_{i}^{{\dagger} }| {b}_{i}\rangle \end{array}$$

(26)

where now U = ⨂_i∈[n]C_i ∈ Cl(1)^⊗n.

Any QEM strategy necessarily incurs a sampling overhead dependent on the amount of noise^95,96,97,98. For global Clifford shadows, Chen et al.⁸⁵ show that the sample complexity is augmented by a factor of ${{{\mathcal{O}}}}({F}_{Z}{({{{\mathcal{E}}}})}^{-2})$ for estimating observables with constant Hilbert–Schmidt norm, where ${F}_{Z}({{{\mathcal{E}}}})={2}^{-n}{\sum }_{b\in {\{0,1\}}^{n}}\langle \!\langle b| {{{\mathcal{E}}}}| b\rangle \!\rangle$ is the average Z-basis fidelity of ${{{\mathcal{E}}}}$. Meanwhile for local Clifford shadows, they prove that product noise of the form ${{{\mathcal{E}}}}= {\bigotimes}_{i\in [n]}{{{{\mathcal{E}}}}}_{i}$, satisfying ${\min }_{i\in [n]}{F}_{Z}({{{{\mathcal{E}}}}}_{i})\ge 1-\xi$, exhibits an overhead factor of ${e}^{{{{\mathcal{O}}}}(k\xi )}$ for estimating k-local qubit observables.

Symmetry-adjusted classical shadows

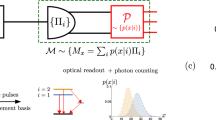
The primary contribution of this paper, symmetry-adjusted classical shadows, is visualized in Fig. 1. We describe it in detail now. Consider a classical shadows protocol over G with target observables O₁, …, O_L. Without loss of generality, let each O_j ∈ V_λ for some subset of irreps $\lambda \in {R}^{{\prime} }\subseteq {R}_{G}$. Suppose the experiment experiences an unknown noise channel ${{{\mathcal{E}}}}$ obeying Assumptions 1.

Fig. 1: Schematic of the symmetry-adjusted classical shadows protocol.

a Given an ideal unitary ${{{\mathcal{U}}}}(\cdot )=U(\cdot ){U}^{{\dagger} }$, its noisy implementation is denoted by $\widetilde{{{{\mathcal{U}}}}}$. Assuming the target state $\rho ={{{{\mathcal{U}}}}}_{{{{\rm{prep}}}}}(\left\vert {0}^{n}\right\rangle \!\left\langle {0}^{n}\right\vert )$ obeys certain symmetries S_λ, b we can construct error-mitigated estimates using classical shadows produced by the noisy quantum computer. (While we depict the preparation of a pure state here, our formalism is equally valid if the target state is mixed.) In contrast to prior approaches that only address the noise in ${\widetilde{{{{\mathcal{U}}}}}}_{g}$, our protocol additionally incorporates the errors within ${\widetilde{{{{\mathcal{U}}}}}}_{{{{\rm{prep}}}}}$. c Our method is applicable whenever the symmetry is compatible with the irreps V_λ of the group G describing the classical shadows protocol.

We show that, if ρ obeys symmetries which are “compatible” with the irreps in ${R}^{{\prime} }$, then it is possible to construct an estimator which accurately predicts the ideal, noiseless observables. By compatible, we mean that there exist symmetry operators S_λ ∈ V_λ for each $\lambda \in {R}^{{\prime} }$ for which their ideal expectation values

$${s}_{\lambda }:={{{\rm{tr}}}}({S}_{\lambda }\rho )$$

(27)

are known a priori. In general, there is no reason to expect that a physical system has symmetries which exactly fit into the irreps of a classical-shadow measurement scheme. However, given a symmetry operator S, it is always possible to project it to V_λ using the superoperator projector Π_λ, i.e., S_λ = Π_λ(S).

Then, using noisy classical shadows $\hat{\rho }(T)$ of size T, we construct error-mitigated estimates as

$${\hat{o}}_{j}^{{{{\rm{EM}}}}}(T):=\frac{{{{\rm{tr}}}}({O}_{j}\hat{\rho }(T))}{{{{\rm{tr}}}}({S}_{\lambda }\hat{\rho }(T))/{s}_{\lambda }}.$$

(28)

We find that the relevant noise characterization in this scenario is

$${F}_{Z,{R}^{{\prime} }}({{{\mathcal{E}}}}):={\min }_{\lambda \in {R}^{{\prime} }}\frac{{{{\rm{tr}}}}({{{\mathcal{E}}}}{{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })}{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })},$$

(29)

which can be seen as a generalization of the noise fidelity ${F}_{Z}({{{\mathcal{E}}}})$ described in the “Background” subsection. Here, ${F}_{Z,{R}^{{\prime} }}({{{\mathcal{E}}}})$ only considers how the noise channel acts within the irreducible subspaces of interest.

As two key applications, we study how symmetry-adjusted classical shadows perform in simulations of fermionic and qubit systems. For fermions, we consider G corresponding to fermionic Gaussian unitaries⁶⁹ (also known as matchgate shadows⁷⁰). We establish the following performance bound for fermionic systems with particle-number symmetry, $N={\sum }_{p\in [n]}{a}_{p}^{{\dagger} }{a}_{p}$.

Theorem 1

(Fermions with particle-number symmetry, informal). Let ρ be an n-mode state with ${{{\rm{tr}}}}(N\rho )=\eta$ fermions. Under the noise model ${{{\mathcal{E}}}}$ satisfying Assumptions 1 and assuming $\eta ={{{\mathcal{O}}}}(n)$, matchgate shadows of size

$$T={{{\mathcal{O}}}}({n}^{2}\log (n){\epsilon }^{-2}{F}_{Z,\{2,4\}}{({{{\mathcal{E}}}})}^{-2})$$

(30)

suffice to achieve prediction error

$$| {\hat{o}}_{j}(T)-{{{\rm{tr}}}}({O}_{j}\rho )| \le \epsilon +{{{\mathcal{O}}}}({\epsilon }^{2})$$

(31)

with high probability, where the observables O_j can be taken as all one- and two-body Majorana operators.

The dependence on system size n and prediction error ϵ matches noiseless estimation with matchgate shadows^69,70. Meanwhile, the overhead of error mitigation is ${{{\mathcal{O}}}}({F}_{Z,{R}^{{\prime} }}{({{{\mathcal{E}}}})}^{-2})$, analogous to prior related results^85,86. The irreps ${R}^{{\prime} }=\{2,4\}$ correspond to the Majorana degree of the k-body observables.

For qubit systems, we consider G essentially corresponding to the local Clifford group (i.e., random Pauli measurements)^51,52. In order to make the irreducible structure compatible with commonly encountered symmetries, we introduce a technical modification that we call subsystem-symmetrized Pauli shadows (see the subsection “Subsystem-symmetrized Pauli shadows” for a summary). The symmetry we consider here is generated by the total longitudinal magnetization, M = ∑_i∈[n]Z_i. For error-mitigated prediction of local qubit observables, we have the following result.

Theorem 2

(Qubits with total magnetization symmetry, informal). Let ρ be an n-qubit state with a fixed magnetization, ${{{\rm{tr}}}}(M\rho )=m$. Under the noise model ${{{\mathcal{E}}}}$ satisfying Assumptions 1 and assuming m = Θ(1), subsystem-symmetrized Pauli shadows of size

$$T={{{\mathcal{O}}}}(n\log (n){\epsilon }^{-2}{F}_{Z,\{1,2\}}{({{{\mathcal{E}}}})}^{-2})$$

(32)

suffices to achieve prediction error

$$| {\hat{o}}_{j}(T)-{{{\rm{tr}}}}({O}_{j}\rho )| \le \epsilon +{{{\mathcal{O}}}}({\epsilon }^{2})$$

(33)

with high probability, where the observables O_j can be taken as all one- and two-local Pauli operators.

Note that the irreps of subsystem-symmetrized Pauli shadows are labeled by Pauli weight. The variance bound we advertise here is linear in n, resulting from the extensive nature of the symmetry M. Specifically, we show that when m = Θ(1), $\parallel M{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}(n)$ dominates the asymptotic complexity over the k-local Pauli observables (for which our protocol exhibits the usual $\parallel {O}_{j}{\parallel }_{{{{\rm{shadow}}}}}^{2}={3}^{k}$). This is consistent with standard Pauli shadows, wherein the shadow norm of arbitrary k-local observables scales at most linearly with spectral norm and exponentially in k^51,52.

Besides these two examples, we describe symmetry-adjusted classical shadows for a more general class of groups G, and we establish accompanying bounds in Theorem 4 in the Methods section (proven in Supplementary Note 1). This allows for applications to other systems and unitary distributions. See “Theory of symmetry-adjusted classical shadows” in the Methods section for the general theory, and subsections “Application to fermionic (matchgate) shadows” and “Application to qubit (Pauli) shadows” for the details regarding Theorems 1 and 2, respectively.

Because our protocol always runs the full noisy quantum circuit, it has the potential to mitigate a wider range of errors than those covered by Assumptions 1, albeit without the rigorous theoretical guarantees. This is a significant feature of the method, as the preparation of ρ often dominates the total circuit complexity (i.e., U_prep in Fig. 1). We explore this broader mitigation potential with a series of numerical experiments below, wherein we simulate noisy Trotter circuits for systems of interacting fermions and spin-1/2 particles, respectively.

Subsystem-symmetrized Pauli shadows

While random Pauli measurements are efficient for predicting local qubit observables, the irreducible structure of the local Clifford group Cl(1)^⊗n is difficult to reconcile with common symmetries under symmetry adjustment, such as the U(1) symmetry generated by M = ∑_i∈[n]Z_i. To remedy this issue, we modify the protocol by what we call subsystem symmetrization: define the group

$${{{\rm{Cl}}}}{(1)}_{{{{\rm{Sym}}}}}^{\otimes n}:={{{\rm{Sym}}}}(n)\times {{{\rm{Cl}}}}{(1)}^{\otimes n},$$

(34)

which has the unitary representation U_(π, C) = S_πC where S_π permutes the qubits according to π ∈ Sym(n) and C ∈ Cl(1)^⊗n. The circuit for S_π can be obtained as a sequence of ${{{\mathcal{O}}}}({n}^{2})$ nearest-neighbor SWAP gates in ${{{\mathcal{O}}}}(n)$ depth via an odd–even decomposition of π⁹⁹. The following theorem summarizes its group-theoretic properties relevant to classical shadows.

Theorem 3

(Irreducible representations of the subsystem-symmetrized local Clifford group). The representation ${{{\mathcal{U}}}}:{{{\rm{Cl}}}}{(1)}_{{{{\rm{Sym}}}}}^{\otimes n}\to {{{\rm{U}}}}({{{\mathcal{L}}}}({{{\mathcal{H}}}}))$, defined by ${{{{\mathcal{U}}}}}_{(\pi ,C)}(\rho )={S}_{\pi }C\rho {C}^{{\dagger} }{S}_{\pi }^{{\dagger} }$, decomposes into the irreps

$${V}_{k}={{{\rm{span}}}}\{P\in {{{\mathcal{P}}}}(n):| P| =k\},\quad 0\le k\le n.$$

(35)

Under this group, the (noiseless) expressions for ${{{\mathcal{M}}}}$ and ${{{\rm{Var}}}}[\hat{o}]$ coincide with those of standard Pauli shadows.

This modification therefore reduces the number of irreps from 2ⁿ to n + 1, achieved by symmetrizing, for each k, over all k-qubit subsystems. Meanwhile, the desirable estimation properties from standard Pauli shadows are retained: for instance, the shadow norm obeys $\parallel P{\parallel }_{{{{\rm{shadow}}}}}^{2}={3}^{k}$ for k-local Pauli operators P.

The upshot is that the symmetry M is now compatible with this group, thereby enabling results such as Theorem 2. We describe this construction in “Application to qubit (Pauli) shadows” in the Methods section, with technical proofs in Supplementary Note 2.

Spin-adapted matchgate shadows

Systems of spinful fermions often obey a spin symmetry, which allows for compressed block-diagonal representations according to the spin sectors. Such techniques are referred to as symmetry adaptation. We introduce such an adaptation of the matchgate shadows protocol wherein the random distribution is restricted to block-diagonal orthogonal transformations,

$$Q=\left(\begin{array}{cc}{Q}_{\uparrow }&0\\ 0&{Q}_{\downarrow }\end{array}\right)\in {{{\rm{O}}}}(n)\oplus {{{\rm{O}}}}(n).$$

(36)

We call this protocol spin-adapted matchgate shadows. This restricted group remains informationally complete over operators which respect the spin sectors, thus sufficing for learning properties in systems with this symmetry. In fact, we show that the shadow norms for k-fermion operators under the spin-adapted protocol scale identically as in the unadapted setting. The main advantage of spin adaptation is that the block-diagonal transformation Q = Q_↑ ⊕ Q_↓ can be implemented as ${U}_{{Q}_{\uparrow }}\otimes {P}_{\downarrow }^{s}{U}_{{Q}_{\downarrow }}$, where P_↓ = Z^⊗n/2 is the parity operator on the spin-down sector and $s={\delta }_{-1,\det {Q}_{\uparrow }}$. This tensor-product unitary requires roughly half the number of gates and circuit depth compared to implementing a dense element of O(2n). We prove the necessary details in Supplementary Note 3 and implement this modified protocol in our numerical experiments wherever applicable.

Improved circuit design for fermionic Gaussian unitaries

Fermionic Gaussian unitaries are a broad class of free-fermion rotations, and they are ubiquitous primitives in algorithms for simulating (interacting) fermions. In the context of classical shadows, they form the basis for randomized measurements in matchgate shadows^69,70,71. Such unitaries can be described by an orthogonal transformation Q ∈ O(2n) of the Majorana operators,

$${{{{\mathcal{U}}}}}_{Q}({\gamma }_{\mu })={U}_{Q}{\gamma }_{\mu }{U}_{Q}^{{\dagger} }=\mathop{\sum}\limits_{\nu \in [2n]}{Q}_{\nu \mu }{\gamma }_{\nu }$$

(37)

for each μ ∈ [2n]. The quantum circuits implementing these transformations take ${{{\mathcal{O}}}}({n}^{2})$ gates in ${{{\mathcal{O}}}}(n)$ depth^100,101. While this scaling is necessary in general by parameter counting, constant-factor savings can substantially improve performance in practice, especially on noisy quantum computers.

To this end, we introduce a more efficient compilation scheme for fermionic Gaussian unitaries, given an arbitrary Q ∈ O(2n). Our circuit design improves the parallelization of gates compared to prior art^100,101. The key idea is to observe that two Majorana modes essentially correspond to one qubit under the Jordan–Wigner transformation¹⁰². Thus, the optimal approach to compiling U_Q into single- and two-qubit gates involves decomposing the matrix Q into elementary blocks of 4 × 4 transformations, rather than the 2 × 2 Givens rotations utilized in prior designs.

The details of this scheme are described in Supplementary Note 4 and implemented in code at our open-source repository (https://github.com/zhao-andrew/symmetry-adjusted-classical-shadows). We make use of this improved design in our numerical simulations. We demonstrate the improvements in circuit size in Fig. 2, with respect to a gate set native to superconducting platforms. From these results we numerically infer roughly 1/3 reduction in depth and 1/2 reduction in gate count over prior designs.

Fig. 2: Resource comparison of our improved fermionic Gaussian circuit design versus prior designs.

Our circuit costs (green) are compared against those of Jiang et al.¹⁰⁰ (blue), implemented in OpenFermion¹³², and a naive scheme described in Supplementary Note 4 (red). All circuits were optimized to a superconducting gate set consisting of $\sqrt{{{{\rm{i}}}}{{{\rm{SWAP}}}}}$ gates and single-qubit rotations. We compare both a circuit depth and b gate count on random inputs Q ∈ O(2n). Linear and quadratic fits are made, demonstrating a roughly 3 × and 2 × savings, respectively.

Numerical experiments

We now demonstrate the error-mitigation capabilities of symmetry-adjusted classical shadows through numerical simulations. We focus on the task of estimating one- and two-body observables in both fermion and qubit systems which obey the global U(1) symmetries described in the Methods section.

For each type of system, we first present results when the noise models obey Assumptions 1 (readout errors). We demonstrate the successful mitigation at varying sample sizes, noise rates, and system sizes, confirming the correctness of our theory.

Next, we investigate how symmetry adjustment performs under a more comprehensive noise model based on superconducting-qubit platforms. These simulations were performed using the Quantum Virtual Machine (QVM) within the Cirq open-source software package^93,103. It uses existing hardware data on a native gate set (single-qubit rotations and two-qubit $\sqrt{{{{\rm{i}}}}{{{\rm{SWAP}}}}}$ gates on a square lattice) to mimic the realistic performance of a noisy quantum computer. We use the calibration data provided of Google’s 23-qubit Rainbow processor based on the Sycamore architecture, which was used in quantum experiments simulating quantum chemistry and strongly correlated materials^33,35. The noise model consists of depolarizing channels, two-qubit coherent errors, single-qubit idling noise, and readout errors. Error rates vary across the chip; on the 2 × 4 grid that we simulated, the average single- and two-qubit Pauli error rates are ~0.15% and ~1.5%, respectively. A precise description of the noise model can be found in Supplementary Note 6.

Throughout, we use the following conventions for figures. Noiseless data (blue squares) correspond to simulations of an ideal quantum computer, which experiences no noise channel and only exhibits the fundamental sampling error. Unmitigated data (black X’s) are simulations of classical shadows on a noisy quantum computer, using standard postprocessing routines. The mitigated estimates (red diamonds) are instead postprocessed as symmetry-adjusted classical shadows, as described in the Methods section. In some experiments, we also compare against robust shadow estimation⁸⁵ (RShadow, green crosses), which involves simulating the calibration protocol on $\left\vert {0}^{n}\right\rangle$ under the same noise model. Finally, the true values (teal curves) are the ground truth, against which we determine the prediction error.

Uncertainty bars represent one standard deviation of the combined sampling and postprocessing, computed by empirical bootstrapping¹⁰⁴. To ease the computational load, we slightly modify the procedure by batching samples; see Supplementary Note 6 for details.

Fermionic systems

Our first set of numerical experiments consider the application to matchgate shadows to learn and mitigate noise in one- and two-body fermionic observables. The symmetry we consider is fixed particle number, ${{{\rm{tr}}}}(N\rho )=\eta$. As we show in the Methods section, this symmetry projects into the relevant irreps ${R}^{{\prime} }=\{2,4\}$ of the matchgate shadows as

$${S}_{2}={\Pi }_{2}(N)=-\frac{1}{2}\mathop{\sum}\limits_{p\in [n]}{Z}_{p},$$

(38)

$${S}_{4}={\Pi }_{4}({N}^{2})=\frac{1}{2}\mathop{\sum}\limits_{p < q}{Z}_{p}{Z}_{q},$$

(39)

represented under the Jordan–Wigner transformation¹⁰² for simplicity. Their ideal values are

$${s}_{2}={{{\rm{tr}}}}\left({S}_{2}\rho \right)=\eta -\frac{n}{2},$$

(40)

$${s}_{4}={{{\rm{tr}}}}\left({S}_{4}\rho \right)=\frac{1}{2}\left(\begin{array}{c}n\\ 2\end{array}\right)-\eta (n-\eta ).$$

(41)

Readout noise model (fermions)

First, we consider the reconstruction of the fermionic two-body reduced density matrix (2-RDM) from matchgate shadows. The 2-RDM elements of a state ρ are given by

$${}^2D_{rs}^{pq}={{{\rm{tr}}}}\left({a}_{p}^{{\dagger}}{a}_{q}^{{\dagger}}{a}_{s}{a}_{r}\rho \right),\quad p,q,r,s\in [n].$$

(42)

In general, knowledge of the k-RDM allows one to calculate any k-body observable of the system. By anticommutation relations, there are only ${\left(\begin{array}{c}n\\ 2\end{array}\right)}^{2}$ unique matrix elements, corresponding to the indices p < q and r < s. We therefore represent ²D as an $\left(\begin{array}{c}n\\ 2\end{array}\right)\times \left(\begin{array}{c}n\\ 2\end{array}\right)$ Hermitian matrix, flattening along those index pairs. Estimates ${}^{2}{\hat{D}}_{rs}^{pq}(T)={{{\rm{tr}}}}({a}_{p}^{{\dagger} }{a}_{q}^{{\dagger} }{a}_{s}{a}_{r}\hat{\rho }(T))$ are computed from T matchgate-shadow samples. Here, our figure of merit for the prediction error is the spectral-norm difference between the reconstructed and the numerically exact 2-RDMs, $\epsilon ={\parallel }^{2}\hat{D}{-}^{2}D{\parallel }_{\infty }$.

We demonstrate 2-RDM reconstruction on an ensemble of 20 random Slater determinants (noninteracting-fermion states with fixed particle number). An η-fermion Slater determinant is specified by the first η columns of an n × n unitary matrix, so we generate the random states by uniformly drawing elements of U(n). This n × n representation is then lifted to the 2n × 2n fermionic Gaussian representation, which allows us to apply the random matchgate transformations Q ∈ B(2n) efficiently. This simulates the action of $\rho \mapsto {U}_{Q}\rho {U}_{Q}^{{\dagger} }$. The measurement is then simulated using the algorithm of [ref. ¹⁰⁵, Sec. 5.1]. Finally, to simulate the readout noise we implement the effective noise channel on the sampled bit strings offline.

While the 2-RDM of free-fermion states can be computed from the 1-RDM using Wick’s theorem, we do not employ any such tricks here; we use Slater determinants simply to facilitate fast classical simulation. We also do not use any additional error-mitigation strategies, such as RDM positivity constraints¹⁰⁶, that could in principle be applied in tandem.

The results are presented in Fig. 3. We consider a small system size, n = 8 and η = 2, and simulate three types of single-qubit noise channels before readout: depolarizing, amplitude damping, and bit flip. The noise rate p represents the probability of such an error occurring, independently on each qubit (defined in Supplementary Note 6). In the top row, we show how the prediction error varies with the total number of samples T. As expected, the noiseless estimates (corresponding to p = 0) converge as ~T^−1/2, which is the standard shot-limited behavior. Then, setting p = 0.2, we see how the unmitigated data experiences an error floor beyond which taking additional samples does not improve the accuracy. On the other hand, the mitigated results clearly bypass this error floor and recover the shot-noise scaling with T, thus validating the theory of symmetry-adjusted classical shadows. Compared to the noiseless simulations, our mitigated data exhibit a constant factor increase in the sampling cost, corresponding to the ${{{\mathcal{O}}}}({F}_{Z,{R}^{{\prime} }}^{-2})$ overhead of error mitigation, as it appears in Theorem 4.

Fig. 3: Estimation error of the fermionic 2-RDM reconstructed from matchgate shadows.

Error is quantified by the spectral-norm difference between the estimated and true 2-RDM. We simulate the protocol on a collection of 20 random Slater determinants on n = 8 modes with η = 2 fermions; faint dashes are results for individual states, markers indicate the median error across the 20 states. a Scaling of estimation error with the total number of samples T, fixing the noise rate to p = 0.2 for all noise models. b Scaling of the estimation error with the noise rate p, fixing the total number of samples to T = 10⁶.

For these experiments, we also compare to the performance of robust shadow estimation (RShadow) by Chen et al.⁸⁵, which requires simulating the calibration procedure on $\left\vert {0}^{n}\right\rangle$. For a fair comparison, we allocate T/2 samples to the calibration step and T/2 samples to the estimation step, so that the total number of samples is the same. While Chen et al.⁸⁵ did not originally consider matchgate shadows, from our generalization in Eq. (23) we can construct NoiseEst_B(2n) by taking D_λ = S_2k, which obeys 〈0ⁿ∣S₂∣0ⁿ〉 = − n/2 and 〈0ⁿ∣S₄∣0ⁿ〉 = n(n − 1)/4. The single-shot estimator is then

$${{{{\rm{NoiseEst}}}}}_{{\rm{B}}(2n)}(2k,Q,b)=\frac{\langle b| {U}_{Q}{S}_{2k}{U}_{Q}^{{\dagger} }| b\rangle }{\langle {0}^{n}| {S}_{2k}| {0}^{n}\rangle }.$$

(43)

As expected, RShadow behaves similarly to symmetry-adjusted classical shadows in this scenario (wherein the noise obeys Assumptions 1). However, even here we observe that our approach exhibits a constant-factor advantage in the sampling cost. We attribute the performance of RShadow to its calibration procedure, which our method avoids.

In the bottom row of Fig. 3, we simulate the same collection of random Slater determinants, but now varying the noise rate p at a fixed shadow size T = 10⁶. While the unmitigated errors quickly grow with increasing noise rate as expected, the mitigated estimates remain under control. Note that the mitigated errors still grow modestly because we have fixed the number of samples; in order to achieve a constant prediction error, one would need to grow T proportional to ${F}_{Z,{R}^{{\prime} }}^{-2}$ (which is p-dependent). Our key takeaway is that the combination of both rows of plots indicates the ability to handle a range of common noise channels at fairly high error rates. Indeed, the growing errors seen in the bottom row can be suppressed by simply taking more samples, which is precisely what the top row demonstrates.

Next, we consider the simulation of a 1D spinful Fermi–Hubbard chain of L = n/2 sites (for a total of n fermionic modes/qubits). Under open boundary conditions, the Hamiltonian for this model is

$$H=J+V,$$

(44)

where

$$J=-t\mathop{\sum}\limits_{i\in [L-1]}\mathop{\sum}\limits_{\sigma \in \{\uparrow ,\downarrow \}}{a}_{i,\sigma }^{{\dagger} }{a}_{i+1,\sigma }+\,{{\mbox{h.c.}}}\,,$$

(45)

$$V=U\mathop{\sum}\limits_{i\in [L]}{N}_{i,\uparrow }{N}_{i,\downarrow },$$

(46)

are the hopping and interaction terms, respectively. The creation operators ${a}_{i,\sigma }^{{\dagger} }$ produce an electron at site i with spin σ, and ${N}_{i,\sigma }={a}_{i,\sigma }^{{\dagger} }{a}_{i,\sigma }$ is the associated occupation-number operator. We set units such that the hopping strength is t = 1.

For the target state, we use the ground state of the noninteracting term J, which is also a Slater determinant. This allows us to use the same simulation techniques as before to efficiently simulate up to 20 sites. The number of electrons in each spin sector is η_σ = L/2, for a total of η = η_↑ + η_↓ = n/2 electrons. Thus the system is at half filling, which requires the use of ancilla qubits to avoid division by zero (see the Methods section). In fact, we simulate ${n}^{{\prime} }=n+2$ qubits because we append an ancilla qubit to each spin sector. This is because we furthermore employ spin-adapted matchgate shadows, as described previously in the Results section. This modification essentially treats each spin sector independently when performing the randomized measurements, so each sector is at half filling.

The Fermi–Hubbard results are shown in Fig. 4. We consider the estimation of energy per electron, 〈H〉/η. We set the interaction strength to U/t = 4 and the noise model to single-qubit bit-flip errors, with probabilities p ∈ {0.01, 0.03, 0.05}. The energy per electron (top) and absolute estimation error (bottom) are plotted as the system size grows, keeping the number of samples fixed to T = 2 × 10⁶. Again, these results serve to validate our theory, this time highlighting the performance as the system size grows. This also demonstrates the use of spin-adapted matchgate shadows and the successful use of ancillas to avoid division by zero in ${\hat{o}}_{j}^{{{{\rm{EM}}}}}$.

Fig. 4: Estimation of the energy per electron of a 1D spinful Fermi–Hubbard model.

We consider an interaction strength U/t = 4 on 4 ≤ L ≤ 20 sites, and we measure 〈H〉/η using spin-adapted matchgate shadows with T = 2 × 10⁶ samples. We simulate the protocol on the ground state of the noninteracting component J of the Hamiltonian, Eq. (45), at half filling in each spin sector, which is a Slater determinant with η_σ = L/2 electrons per sector. These simulations involve ${n}^{{\prime} }=2L+2$ noisy qubits experiencing readout bit-flip errors with probabilities 1%, 3%, and 5%. The additional qubit per spin sector is prepared in $\left\vert 0\right\rangle$ to avoid division by zero (see the Methods section). Error bars denote one standard error of the mean.

QVM noise model (fermions)

Now we turn to the gate-level noise model simulated through the QVM^93,103. This model strongly violates Assumptions 1, reflecting the fact that the state-preparation circuit U_prep is typically the dominant source of errors.

As our testbed fermionic system, we again consider the 1D spinful Fermi–Hubbard chain with open boundary conditions and interaction strength U/t = 4. Rather than the static problem, here we simulate Trotterized time evolution of the Hamiltonian. The number of Trotter steps provides a systematic way to increase the circuit depth (and hence the cumulative amount of noise) within the same model. Note that because we are studying the behavior of error mitigation, the ground truth of these simulations corresponds to the noiseless Trotter circuit with a finite step size (i.e., we are not comparing to the exact, non-Trotterized dynamics).

We closely follow the setup of the experiment performed in ref. ³⁵ (which was in fact performed on the Sycamore processor that our noise model is based on), using code made available by the authors at ref. ¹⁰⁷. Because simulating the full noisy circuit is exponentially expensive, we restrict to a four-site instance (n = 2L = 8). The initial state is the ground state in the η_↑, η_↓ = 1 sector of the noninteracting Hamiltonian

$${H}_{0}=J+\mathop{\sum}\limits_{i\in [L]}\mathop{\sum}\limits_{\sigma \in \{\uparrow ,\downarrow \}}{\varepsilon }_{i,\sigma }{N}_{i,\sigma },$$

(47)

where J is the hopping term defined in Eq. (45) and we set the on-site potentials to have a Gaussian form, ${\varepsilon }_{i,\sigma }=-{\lambda }_{\sigma }{e}^{-\frac{1}{2}{(i+1-c)}^{2}/{s}^{2}}$. This generates a Slater determinant whose charge density

$${\varrho }_{i}=\langle {N}_{i,\uparrow }+{N}_{i,\downarrow }\rangle .$$

(48)

has a Gaussian profile, centered around c with width s and magnitude λ_σ. We set the parameters to c = L/2 + 1/2 = 2.5, s = 7/3, and λ_σ = 4δ_σ,↑. This initial state is prepared by the appropriate single-particle basis rotations^100,108,109 on the state $\left\vert 1000\right\rangle$ within each spin sector. Denote this unitary by U(H₀). The system is then evolved by Trotterized dynamics according to H, with R ∈ {0, 1, …, 5} steps of size δt = 0.2. Let J_even (resp., J_odd) be the terms in J with i even (resp., odd), and similarly for V_even, V_odd. One Trotter step is ordered as

$${U}_{{{{\rm{Trot}}}}}={e}^{-{{{\rm{i}}}}{J}_{{{{\rm{odd}}}}}\delta t}{e}^{-{{{\rm{i}}}}{V}_{{{{\rm{odd}}}}}\delta t}{e}^{-{{{\rm{i}}}}{V}_{{{{\rm{even}}}}}\delta t}{e}^{-{{{\rm{i}}}}{J}_{{{{\rm{even}}}}}\delta t},$$

(49)

which is then compiled into the native gate set. The full state-preparation circuit is then

$${U}_{{{{\rm{prep}}}}}(R)={U}_{{{{\rm{Trot}}}}}^{R}U({H}_{0}){X}_{0,\downarrow }{X}_{0,\uparrow },$$

(50)

where X_0,σ places a spin-σ electron on the first site from the vacuum (i.e., prepares $\left\vert 1000\right\rangle$ in each spin sector). Note that R = 0 corresponds to only preparing the initial Slater determinant, which still has nontrivial circuit depth. Further details on the construction of these circuits can be found in refs. ^35,107.

One final detail of ref. ³⁵ that we follow is their method of qubit assignment averaging (QAA). This technique is employed as a means of ameliorating inhomogeneities in error rates across the quantum device. QAA works by identifying a collection of different assignments for the physical qubit labels and uniformly averaging over them (keepng the Jordan–Wigner convention fixed). For example, one may vary qubit assignments by selecting a different portion of the chip, or rotating/flipping the layout. Here, we fix a 2 × 4 grid of qubits and perform QAA over four different orderings of those eight qubits; see Supplementary Note 6 for the specific assignments chosen.

For each target state ${U}_{{{{\rm{prep}}}}}(R)\left\vert {0}^{n}\right\rangle$, we collect T = 9.6 × 10⁵ spin-adapted matchgate shadow samples. In Fig. 5, we plot the Trotterized time evolution of charge density throughout the chain, as well as the charge spread

$$\kappa =\mathop{\sum}\limits_{i\in [L]}\left\vert i-(L-1)/2\right\vert {\varrho }_{i},$$

(51)

which quantifies how the density spreads away from the center of the chain. These quantities are only one-body observables, so as an exemplary two-body observable we also estimate the energy per electron, 〈H〉/η.

Fig. 5: Prediction of local properties in the four-site 1D Fermi–Hubbard model undergoing Trotterized time evolution.

The interaction strength is set to U/t = 4 and the Trotter step size is δt = 0.2. The noise model is that of the Google Sycamore Rainbow processor^33,35, implemented within the Cirq QVM^93,103. The size of the noisy circuit grows systematically with the number of Trotter steps. We use spin-adapted matchgate shadows, taking T = 9.6 × 10⁵ samples. a Charge density ϱ_i at each site i ∈ [L]. b Charge spread κ. c Energy per electron 〈H〉/η. Error bars denote one standard error of the mean.

Because Assumptions 1 no longer hold, we no longer have the guarantees of Theorem 4 and we do not observe an arbitrary amount of error mitigation. We see that as the circuit size grows, so too do the prediction error and uncertainty. This behavior is a reflection of the noise assumptions being increasingly violated. Nonetheless, our results still show a substantial amount of noise reduction, and overall we maintain the qualitative features of the dynamics compared to the unmitigated protocol. In Supplementary Note 6, we provide a quantitative estimate of how much the QVM noise model violates Assumptions 1. There we observe a fundamental error floor, which is roughly an order of magnitude below the mitigated errors actually achieved here, indicating the potential for further mitigation beyond what we have presently demonstrated.

Qubit systems

Next, we study the application of symmetry-adjusted classical shadows to subsystem-symmetrized Pauli shadows, to predict one- and two-body qubit observables in the presence of noise. We consider a fixed magnetization symmetry ${{{\rm{tr}}}}(M\rho )=m$, which, as we show in the Methods section, projects into the relevant irreps ${R}^{{\prime} }=\{1,2\}$ as

$${S}_{1}={\Pi }_{1}(M)=\mathop{\sum}\limits_{i\in [n]}{Z}_{i},$$

(52)

$${S}_{2}={\Pi }_{2}({M}^{2})=2\mathop{\sum}\limits_{i < j}{Z}_{i}{Z}_{j}.$$

(53)

The ideal symmetry values in this case are

$${s}_{1}=m,$$

(54)

$${s}_{2}={m}^{2}-n.$$

(55)

Readout noise model (qubits)

For our first demonstration, we simulate random matrix product states (MPS) with maximum bond dimension χ ≤ n, lying in the m = 0 symmetry sector of M. We use the definition of a random MPS from refs. ^110,111. Numerically, we implement all MPS calculations using the open-source software ITensor¹¹², which can guarantee the correct symmetry sector using efficient tensor-network representations. Within such representations, it is straightforward to apply random local Clifford gates and SWAP gates, and to sample measurements in the computational basis.

Unlike fermions, qubits are not symmetrized, so their 2-RDMs

$${}^{2}{D}_{ij}={{{{\rm{tr}}}}}_{[n]\setminus \{i,j\}}\rho$$

(56)

are in general distinct between different two-qubit subsystems. Our accuracy metric here is therefore the mean 2-RDM error over all pairs of qubits:

$$\epsilon =\frac{1}{\left(\begin{array}{c}n\\ 2\end{array}\right)}\mathop{\sum}\limits_{i < j}{\parallel }^{2}{\hat{D}}_{ij}(T){-}^{2}{D}_{ij}{\parallel }_{\infty }.$$

(57)

From subsystem-symmetrized Pauli shadows $\hat{\rho }(T)$ of size T, we reconstruct the qubit 2-RDMs by estimating all one- and two-local Pauli expectation values and forming the 4 × 4 matrices

$${}^{2}{\hat{D}}_{ij}(T)=\frac{1}{4}\mathop{\sum}\limits_{W,{W}^{{\prime} }\in {{{\mathcal{P}}}}(1)}{{{\rm{tr}}}}\left({W}_{i}{W}_{j}^{{\prime} }\hat{\rho }(T)\right)W\otimes {W}^{{\prime} }.$$

(58)

The results are shown in Fig. 6. Similar to the conclusions drawn from Fig. 3 for the fermionic case, we observe that our theory is validated in two important parameters (number of samples and error rate). We note here that this simple demonstration also validates our subsystem-symmetrized Pauli shadows protocol and the use of ancillas in this scenario as well (recall that the random states we study here have vanishing symmetry value, m = s₁ = 0).

Fig. 6: Average estimation error of the 2-RDM over all two-qubit subsystems, reconstructed from (subsystem-symmetrized) Pauli shadows.

Error is quantified by the spectral-norm difference between the estimated and true 2-RDM for each subsystem, taking the mean over all $\left(\begin{array}{c}n\\ 2\end{array}\right)$ subsystems. We simulate the protocol on a collection of 20 random eight-qubit matrix product states, with maximum bond dimension χ ≤ n and fixed Z magnetization, m = 0. Because m = 0 implies s₁ = 0, we simulate a system of nine qubits with the ancilla prepared in $\left\vert 0\right\rangle$. a Scaling of estimation error with the total number of samples T, fixing the noise rate to p = 0.2 for all noise models. b Scaling of the estimation error with the noise rate p, fixing the total number of samples to T = 10⁶.

Our next set of numerical experiments are performed on the ground state of an antiferromagnetic XXZ Heisenberg chain with open boundary conditions:

$$H=J\mathop{\sum}\limits_{i\in [n-1]}\left({X}_{i}{X}_{i+1}+{Y}_{i}{Y}_{i+1}+\Delta {Z}_{i}{Z}_{i+1}\right).$$

(59)

Throughout, we set units such that J = 1 and consider an anisotropy of Δ = 1.5. This Hamiltonian commutes with the symmetry operator M, and in particular the ground state obeys m = 0 (assuming the number of spins n is even). We find the ground state via the density-matrix renormalization group (DMRG) algorithm¹¹³, represented as an MPS; therefore we can employ the same classical simulation algorithms as before. Although m = 0 implies a vanishing conserved quantity for the one-body subspace, s₁ = 0, we do not employ the ancilla technique for these simulations because we will only be interested in predicting strictly two-body observables (for which s₂ = m² − n ≠ 0).

In Fig. 7 we show the mitigation of energy per spin 〈H〉/n at different system sizes and bit-flip rates on each qubit. For these experiments, the number of samples taken is T = 10⁶. Again, the results validate our theory for Pauli-shadow symmetry adjustment over a range of noise rates and system sizes. In particular, although we require estimating the symmetry operator M which has variance ${{{\mathcal{O}}}}(n)$ (as opposed to H/n, which has constant variance), we see that in practice it suffices to take a number of samples constant in system size. This may indicate that our analysis of the worst-case sampling bounds for symmetry-adjusted classical shadows may be overly pessimistic in typical settings.

Fig. 7: Estimation of energy per particle in the 1D XXZ ground state.

We measure 〈H〉/n from T = 10⁶ subsystem-symmetrized Pauli shadows. The anisotropy of the XXZ model is Δ = 1.5. Note that, as an antiferromagnetic model, the ground state exhibits an m = 0 net magnetization symmetry. The noise model is single-qubit bit flip with probabilities p = 1%, 3%, and 5%. Error bars denote one standard error of the mean.

QVM noise model (qubits)

We now turn to simulations using the QVM noise model, taking the same XXZ Heisenberg spin chain (Δ = 1.5 and n = 8) as our testbed system. Similar to our numerical experiments with the Fermi–Hubbard model, we simulate Trotter circuits of the XXZ model starting from a product state within the symmetry sector of m = 0. Again, we will only be interested in strictly two-local observables so we do not employ the ancilla trick here.

Our initial state is a Néel-ordered product state, $\left\vert 01010101\right\rangle ={\prod }_{j\,{{{\rm{odd}}}}}{X}_{j}\left\vert {0}^{n}\right\rangle$. Defining H_even and H_odd as the terms in H with i even and odd, respectively, a single Trotter step is given by

$${U}_{{{{\rm{Trot}}}}}={e}^{-{{{\rm{i}}}}{H}_{{{{\rm{odd}}}}}\delta t}{e}^{-{{{\rm{i}}}}{H}_{{{{\rm{even}}}}}\delta t},$$

(60)

where we take the step size to be δt = 0.2. Hence, the full state-preparation circuit for R steps is

$${U}_{{{{\rm{prep}}}}}(R)={U}_{{{{\rm{Trot}}}}}^{R}\mathop{\prod}\limits_{j\,{{{\rm{odd}}}}}{X}_{j},$$

(61)

which is then compiled into the native gate set. For each R, we collect T = 4.8 × 10⁵ samples using subsystem-symmetrized Pauli shadows. Because the initial state is a simple basis state, we only display results for R ∈ {1, …, 5} for these studies. In line with our Fermi–Hubbard simulations on the QVM, we perform QAA here as well, averaging over twelve different assignments of the same 2 × 4 qubits (see Supplementary Note 6 for details).

First, we consider the spin–spin correlations 〈S_i ⋅ S_j〉, where

$${{{{\boldsymbol{S}}}}}_{i}=\frac{1}{2}\left(\begin{array}{c}{X}_{i}\\ {Y}_{i}\\ {Z}_{i}\end{array}\right),$$

(62)

for all qubit pairs (i, j) throughout the chain. We plot the prediction errors of these correlation functions in Fig. 8, with the unmitigated data in the first row and mitigated data in the second row. We observe that, while the shallower Trotter circuits are well handled by symmetry-adjusted classical shadows, the mitigation power diminishes as the circuit grows deeper. To examine this effect closer, we plot in the bottom two rows of Fig. 8 the correlation functions between the first spin and the rest of the chain. We see that the 〈S₀ ⋅ S₁〉 errors are particularly dominant due to the magnitude of its true value. Although the absolute error is only marginally improved by symmetry adjustment for some of these pairs, the qualitative behavior is more faithfully recovered than in the unmitigated data (wherein the increasing circuit noise washes out the antiferromagnetic correlations).

Fig. 8: Prediction of spin–spin correlations between qubits in the XXZ chain undergoing Trotterized time evolution.

The anistropy in the model is Δ = 1.5, and we take a Trotter step size of δt = 0.2. The noise model is the superconducting-hardware model implemented within the QVM. We take T = 4.8 × 10⁵ subsystem-symmetrized Pauli shadows to estimate the observables. a Heatmaps of estimation errors for 〈S_i ⋅ S_j〉, under unmitigated versus our symmetry-enabled mitigated postprocessing. b Plots of the 〈S₀ ⋅ S_i〉 correlation functions, to show further details of that particular row of the heatmaps. Error bars denote one standard error of the mean.

Next, we consider macroscopic observables in Fig. 9: the Néel order parameter

$$\langle {S}_{{{{\rm{AF}}}}}^{2}\rangle =\frac{1}{{n}^{2}}\mathop{\sum}\limits_{i,j\in [n]}{(-1)}^{i+j}\langle {{{{\boldsymbol{S}}}}}_{i}\cdot {{{{\boldsymbol{S}}}}}_{j}\rangle ,$$

(63)

and the energy per spin 〈H〉/n. Again we see general trends similar to the other QVM simulations: the mitigated results are in closer qualitative agreement with the true values than the unmitigated data, at the cost of larger uncertainty bars, and without arbitrary amounts of error suppression. Symmetry adjustment consistently reduces the absolute error compared to the unmitigated data, although we note that some of the energy estimates are still a few standard deviations away from the true value. This is attributed to the violation of Assumptions 1, and we leave it an open problem of how to further ameliorate this property.

Fig. 9: Prediction of macroscopic observables in the Trotterized XXZ model under the QVM noise model.

Observables are estimated with T = 4.8 × 10⁵ subsystem-symmetrized Pauli shadows. a Néel order parameter $\langle {S}_{{{{\rm{AF}}}}}^{2}\rangle$. b Energy per spin 〈H〉/n. Error bars denote one standard error of the mean.

Discussion

In this paper, we have introduced symmetry-adjusted classical shadows, a QEM protocol applicable to quantum systems with known symmetries. Our approach builds on the highly successful classical-shadow tomography^51,52, modifying the classically computed linear-inversion step according to symmetry information in the presence of noise. Because our strategy is performed in postprocessing on the noisy measurement data, it allows for straightforward combinations with other QEM strategies. As opposed to prior related works^{85,86,87,88,89}, the main advantage of our approach is the use of the entire noisy circuit, thereby bypassing the need for calibration experiments and accounting for errors in state preparation. Meanwhile, in contrast with other symmetry-based strategies^83,90,91,92, we require no additional quantum resources, utilize finer-grained symmetry information, and can easily take advantage of a wider range of symmetries (e.g., particle number as opposed to only parity conservation). We note that, while this work has focused on local observables (linear functions of ρ), classical shadows can seamlessly be used for nonlinear observable estimation as well⁵¹. Because symmetry adjustment works at the level of the shadow channel inversion, our QEM strategy applies within that context just as well.

Overall, our findings reveal that as a low-cost scheme, symmetry-adjusted classical shadows by itself is already potent for practical error mitigation. Our analytical results guarantee the accuracy of prediction under readout noise assumptions. Even when these assumptions are violated in practice, we expect these results to still provide intuition regarding the mitigation behavior. Indeed, this expectation is validated by our numerical experiments with superconducting-qubit noise models on the Cirq QVM^93,103. From these simulations, we have observed substantial quantitative improvement when the cumulative circuit noise is sufficiently weak, and qualitative improvements across all experiments performed.

Along the way, we have developed a number of ancillary results that may also be of independent interest. Of note are (1) the subsystem-symmetrized Pauli shadows, which uniformly symmetrizes the irreps of the local Clifford group among subsystems; (2) an improved circuit compilation scheme for fermionic Gaussian unitaries, which treats Majorana modes on a more natural footing to improve two-qubit gate parallelization; and (3) symmetry-adapted matchgate shadows, which uses block-diagonal transformations within spin sectors to reduce the size of the random matchgate circuits. We expect that these techniques will find broader applicability in quantum simulation beyond the scope of this paper.

A number of pertinent open questions and future directions remain. For simplicity of the protocol, and because of the examples that we focused on, we restricted attention to multiplicity-free groups. However, tools to generalize to nonmultiplicity-free groups already exist, and in the context of character randomized benchmarking¹¹⁴ such an extension has been developed successfully¹¹⁵. It would therefore be useful to extend our ideas similarly, and investigate what effect (if any) multiplicities have on symmetry-adjusted classical shadows.

Regarding the protocols considered, we have focused on local observable estimation in systems with global U(1) symmetry. However, it is worth noting that the n-qubit Clifford group possesses only one nontrivial irrep, making it essentially compatible with any symmetry. Because its shadow norm is exponentially large for local observables, it is an unfavorable choice for typical quantum simulation applications. One may wonder whether the desirable universality of this irrep can nonetheless be harnessed, analogous to how we constructed the subsystem-symmetrized Pauli shadows. A particularly interesting candidate for future studies would be the global SU(2)/Cl(1) control, introduced in ref. ¹¹⁶, which features both a group with high amounts of symmetry and low sample complexity for local observable estimation. Similarly, the single-fermion U(n) basis rotations used in ref. ⁷² would also be a promising option to study. Alternatively, one may consider different classes of symmetries, such as local (rather than global) symmetries.

One key advantage of symmetry adjustment is its flexibility, allowing for easy integration with other error-mitigation strategies. Investigating this interplay is a clear target for future work. Particularly valuable would be other techniques to massage the circuit noise into approximately satisfying Assumptions 1, for instance by randomized compiling¹¹⁷. From our usage of QAA³⁵ in the numerical experiments, we have already shown heuristically that the mere choice of qubit assignments appears to have such an effect.

Indeed, the reliance on such assumptions for rigorous guarantees may be viewed as a limitation of this work. While our numerical results are encouraging, it behooves one to seek a more comprehensive error analysis applicable to a wider range of noise models. For example, while gate-dependent errors are particularly detrimental to our method, they have been closely studied in the context of randomized benchmarking^{118,119,120,121}. The tools developed therein may be valuable to this setting as well. Establishing a better understanding here may also inspire extensions to surpass the limitations of the current theory. We leave such goals to future work.

Note added.—Shortly after our manuscript appeared on the arXiv preprint server, two related works^122,123 subsequently appeared. The former develops a calibration estimator equivalent to our Eq. (43), while the latter analytically studies the effects of gate-dependent noise on Clifford shadow protocols. The formulation and analyses of symmetry-adjusted classical shadows remain original to our manuscript.

Methods

Theory of symmetry-adjusted classical shadows

Here we describe the theory behind the symmetry-adjusted classical shadows estimator. This approach uses known symmetry information about the ideal, noiseless state ρ that we wish to prepare (but are only able to produce a noisy version of). In this section, we describe the idea for an arbitrary multiplicity-free group G; in the subsequent subsections, we will provide concrete applications to the efficient estimation of local fermionic and qubit observables, respectively.

Suppose ρ is a quantum state obeying a known symmetry, corresponding to a collection of operators S_λ ∈ V_λ for which the values s_λ: = 〈〈S_λ∣ρ〉〉 are known a priori. For example, if the system has a symmetry operator S which spans multiple irreps, then we can construct S_λ using the projectors Π_λ:

$$\left.\left\vert {S}_{\lambda }\right\rangle \!\right\rangle ={\Pi }_{\lambda }\left.\left\vert S\right\rangle \!\right\rangle .$$

(64)

By construction, S_λ is an eigenoperator of both ${{{\mathcal{M}}}}$ and $\widetilde{{{{\mathcal{M}}}}}$:

$$\begin{array}{lll}{{{\mathcal{M}}}}\left.\left\vert {S}_{\lambda }\right\rangle \!\right\rangle \,=\,{f}_{\lambda }\left.\left\vert {S}_{\lambda }\right\rangle \!\right\rangle ,\\ \widetilde{{{{\mathcal{M}}}}}\left.\left\vert {S}_{\lambda }\right\rangle \!\right\rangle \,=\,{\widetilde{f}}_{\lambda }\left.\left\vert {S}_{\lambda }\right\rangle \!\right\rangle .\end{array}$$

(65)

If one is interested in only a subset ${R}^{{\prime} }\subseteq {R}_{G}$ of the irreps, then it suffices to only know those symmetries S_λ for which $\lambda \in {R}^{{\prime} }$.

Because the ideal values of s_λ and f_λ are already known, we can use the estimated noisy expectation value of S_λ to build an estimate for ${\widetilde{f}}_{\lambda }$. We start with the standard postprocessing of classical shadows: applying ${{{{\mathcal{M}}}}}^{-1}$ to the measurement outcomes of the noisy quantum experiments produces, in expectation, the effective state

$$\vert \widetilde{\rho }\left\rangle \!\left\rangle :={\mathcal{M}}^{-1}\widetilde{\mathcal{M}}\vert \rho \right\rangle \!\right\rangle =\mathop{\mathbb{E}}\limits_{g \sim G,b \sim {\widetilde{{{{\mathcal{U}}}}}}_{g}\left.\left\vert \rho \right\rangle \!\right\rangle }{{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{g}^{{\dagger} }\left.\left\vert b\right\rangle \!\right\rangle ,$$

(66)

which clearly differs from $\left.\left\vert \rho \right\rangle \!\right\rangle$ when $\widetilde{{{{\mathcal{M}}}}}\,\ne \,{{{\mathcal{M}}}}$. Nonetheless, we can use this noisy data to estimate the value of $\langle \!\langle {S}_{\lambda }| \widetilde{\rho }\rangle \!\rangle$, which is equal to

$$\langle \!\langle {S}_{\lambda }| \widetilde{\rho }\rangle \!\rangle =\frac{{\widetilde{f}}_{\lambda }}{{f}_{\lambda }}{s}_{\lambda }$$

(67)

by Eq. (65). In fact, this relation applies to any O ∈ V_λ:

$$\langle \!\langle O| \widetilde{\rho }\rangle \!\rangle =\frac{{\widetilde{f}}_{\lambda }}{{f}_{\lambda }}\langle \!\langle O| \rho \rangle \!\rangle .$$

(68)

Hence while we use Eq. (67) to learn ${\widetilde{f}}_{\lambda }$ from the symmetry S_λ, this is in turn applicable to all other operators within the same irrep. This leads to the recovery of the ideal expectation values as

$$\langle \!\langle O| \rho \rangle \!\rangle =\frac{\langle \!\langle O| \widetilde{\rho }\rangle \!\rangle }{\langle \!\langle {S}_{\lambda }| \widetilde{\rho }\rangle \!\rangle /{s}_{\lambda }}.$$

(69)

Having established the theory in expectation, we now analyze the implementation in practice. Let T be the number of classical-shadow snapshots, $\left.\left\vert {\hat{\rho }}_{\ell }\right\rangle \!\right\rangle ={{{{\mathcal{M}}}}}^{-1}{{{{\mathcal{U}}}}}_{{g}_{\ell }}^{{\dagger} }\left.\left\vert {b}_{\ell }\right\rangle \!\right\rangle$ for ℓ = 1, …, T, obtained by sampling the noisy quantum computer. Recall that these snapshots converge to $\widetilde{\rho }$ rather than ρ. From their empirical average, $\hat{\rho }(T)=(1/T)\sum\nolimits_{\ell = 1}^{T}{\hat{\rho }}_{\ell }$, we can estimate the lefthand side of Eq. (67) as

$${\hat{s}}_{\lambda }(T):=\langle \!\langle {S}_{\lambda }| \hat{\rho }(T)\rangle \!\rangle .$$

(70)

This in turn provides an estimate for ${\widetilde{f}}_{\lambda }$,

$${\hat{f}}_{\lambda }(T):={f}_{\lambda }\frac{{\hat{s}}_{\lambda }(T)}{{s}_{\lambda }}.$$

(71)

This can be understood as a generalization of NoiseEst_G(λ, g, b) from Eq. (23), making the replacements D_λ → S_λ and $\left\vert {0}^{n}\right\rangle \!\left\langle {0}^{n}\right\vert \to \rho$. Indeed, one can view the calibration state $\left\vert {0}^{n}\right\rangle$ as obeying the symmetries given by its stabilizer group.

Consider the estimation of observables O₁, …, O_L with symmetry-adjusted classcial shadows. If any observable is supported over multiple irreps, then we can always decompose it as a linear combination of basis elements across those irreps. Thus without loss of generality we suppose that each O_j ∈ V_λ for some $\lambda \in {R}^{{\prime} }$. From the same noisy classical shadow $\hat{\rho }(T)$, we also have estimates for their noisy expectation values: ${\mathbb{E}}\langle \!\langle {O}_{j}| \hat{\rho }(T)\rangle \!\rangle =\langle \!\langle {O}_{j}| {\widetilde{\rho }}_{j}\rangle \!\rangle$. Then, following Eq. (69) we can directly construct error-mitigated estimators as

$${\hat{o}}_{j}^{{{{\rm{EM}}}}}(T):=\frac{{\hat{o}}_{j}(T)}{{\hat{s}}_{\lambda }(T)/{s}_{\lambda }},$$

(72)

which converges to 〈〈O_j∣ρ〉〉 in the T → ∞ limit (if Assumptions 1 hold). Because ${\mathbb{E}}[X/Y]\,\ne \,{\mathbb{E}}[X]/{\mathbb{E}}[Y]$ (for nontrivial random variables X and Y), Eq. (72) describes a biased estimator. In the following theorem, we quantify this bias by bounding the total prediction error of ${\hat{o}}_{j}^{{{{\rm{EM}}}}}(T)$. This in turn bounds the number of symmetry-adjusted classical-shadow samples T required.

Theorem 4

Fix accuracy and confidence parameters ϵ, δ ∈ (0, 1). Let O₁, …, O_L be a collection of observables, each supported on an irrep of ${{{\mathcal{U}}}}:G\to {{{\rm{U}}}}({{{\mathcal{L}}}}({{{\mathcal{H}}}}))$ as O_j ∈ V_λ for $\lambda \in {R}^{{\prime} }\subseteq {R}_{G}$. Let S_λ ∈ V_λ be a symmetry operator for each $\lambda \in {R}^{{\prime} }$, for which the ideal values ${s}_{\lambda }={{{\rm{tr}}}}({S}_{\lambda }\rho )$ of the target state ρ are known a priori. Suppose that each noisy unitary satisfies Assumptions 1, ${\widetilde{{{{\mathcal{U}}}}}}_{g}={{{\mathcal{E}}}}{{{{\mathcal{U}}}}}_{g}$, and define the quantities

$${F}_{Z,{R}^{{\prime} }}({{{\mathcal{E}}}}):=\mathop{\min }_{\lambda \in {R}^{{\prime} }}\frac{{{{\rm{tr}}}}({{{\mathcal{E}}}}{{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })}{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })},$$

(73)

$${\sigma }^{2}:=\mathop{\rm{max}}\limits_{1\le j\le L,\lambda \in {R}^{{\prime} }}\left\{{{{\rm{Var}}}}[{\hat{o}}_{j}],{{{\rm{Var}}}}\left[\frac{{\hat{s}}_{\lambda }}{{s}_{\lambda }}\right]\right\}.$$

(74)

Then, a (noisy) classical shadow $\hat{\rho }(T)$ of size

$$T={{{\mathcal{O}}}}\left(\frac{\log ((L+| {R}^{{\prime} }| )/\delta )}{{F}_{Z,{R}^{{\prime} }}{({{{\mathcal{E}}}})}^{2}{\epsilon }^{2}}{\sigma }^{2}\right)$$

(75)

can be used to construct error-mitigated estimates

$${\hat{o}}_{j}^{{{{\rm{EM}}}}}(T):=\frac{{{{\rm{tr}}}}({O}_{j}\hat{\rho }(T))}{{{{\rm{tr}}}}({S}_{\lambda }\hat{\rho }(T))/{s}_{\lambda }}$$

(76)

which obey

$$| {\hat{o}}_{j}^{{{{\rm{EM}}}}}(T)-{{{\rm{tr}}}}({O}_{j}\rho )| \le ({\parallel} {O}_{j}{\parallel }_{\infty }+1)\epsilon +{{{\mathcal{O}}}}({\parallel} {O}_{j}{\parallel }_{\infty }{\epsilon }^{2})$$

(77)

for all 1 ≤ j ≤ L, with success probability at least 1 − δ.

The proof of this statement is provided in Supplementary Note 1. Note that ∥ ⋅ ∥_∞ denotes the spectral (operator) norm. We phrase this result in terms of variances, rather than the state-independent shadow norm, because knowledge about ρ (namely, its symmetries) can potentially provide tighter bounds. Note that the variance is with respect to the effective noisy state $\widetilde{\rho }$, which was defined in Eq. (66).

Let us make a few remarks on this result. First, although the symmetry operators appear in the denominator of Eq. (72), they affect the sample complexity as usual for classical shadows, albeit normalized by the value s_λ of the symmetry sector. Thus the division by ${\hat{s}}_{\lambda }(T)$ does not hinder our control over the variance, except when s_λ = 0 (we furthermore show how to handle such pathological cases in the application examples below). For typical applications, the variance ${{{\rm{Var}}}}[{\hat{s}}_{\lambda }/{s}_{\lambda }]\le {\parallel} {S}_{\lambda }/{s}_{\lambda }{\parallel }_{{{{\rm{shadow}}}}}^{2}$ will be comparable to the baseline variance of estimation, ${{{\rm{Var}}}}[{\hat{o}}_{j}]\le {\max }_{{j}^{{\prime} }}{\parallel} {O}_{{j}^{{\prime} }}{\parallel }_{{{{\rm{shadow}}}}}^{2}$. Additionally, the number of irreps considered is typically $| {R}^{{\prime} }| \ll L$ (for instance, in the concrete examples considered in this work, $| {R}^{{\prime} }|$ is a constant). Thus, we expect that the inclusion of symmetry operators incurs negligible overheads for most applications.

Instead, the primary overhead arises from the fact that error-mitigated estimation necessarily comes at the cost of larger overall variances^95,96,97,98. The quantity

$${F}_{Z,{R}^{{\prime} }}({{{\mathcal{E}}}})=\mathop{\rm{min}}\limits_{\lambda \in {R}^{{\prime} }}\frac{{{{\rm{tr}}}}({{{\mathcal{E}}}}{{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })}{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{\Pi }_{\lambda })}$$

(78)

characterizes an effective noise strength, and it can be seen as a generalization of the average Z-basis fidelity of ${{{\mathcal{E}}}}$,

$${F}_{Z}({{{\mathcal{E}}}})=\frac{{{{\rm{tr}}}}({{{\mathcal{E}}}}{{{{\mathcal{M}}}}}_{Z})}{{{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z})}=\frac{1}{{2}^{n}}\mathop{\sum}\limits_{b\in {\{0,1\}}^{n}}\langle \!\langle b| {{{\mathcal{E}}}}| b\rangle \!\rangle ,$$

(79)

which appears in prior works on noise-robust classical shadows^85,86. In contrast to ${F}_{Z}({{{\mathcal{E}}}})$, the quantity ${F}_{Z,{R}^{{\prime} }}({{{\mathcal{E}}}})$ is a more fine-grained characterization of the noise channel, averaged within the relevant subspaces V_λ. Similar to prior results^{85,86,87,88,89}, the sampling overhead of our error-mitigated estimates also depends inverse quadratically on this noise fidelity.

Finally, the error bound we obtain is ${{{\mathcal{O}}}}({\parallel} {O}_{j}{\parallel }_{\infty }\epsilon )$ when ϵ < 1. Note that ∥O_j∥_∞ = 1 for Pauli and Majorana operators. Our result also features error terms of order ${{{\mathcal{O}}}}({\parallel} {O}_{j}{\parallel }_{\infty }{\epsilon }^{2})$, which reflect the biased nature of ${\hat{o}}_{j}^{{{{\rm{EM}}}}}(T)$ as a ratio of two random variables. Nonetheless, our theorem establishes that this bias vanishes as ϵ² ~ 1/T, so that for sufficiently large T the prediction error is dominated by the standard shot-noise scaling of $\epsilon \sim 1/\sqrt{T}$.

Application to fermionic (matchgate) shadows

The first application of symmetry-adjusted classical shadows that we consider is the estimation of local fermionic observables. This is achieved efficiently by fermionic classical shadows⁶⁹, wherein the group G corresponds fermionic Gaussian unitaries (also referred to as matchgate shadows⁷⁰). We will consider a commonly encountered symmetry in fermionic systems: fixed particle number. However, it will be clear how the general idea can apply to other symmetries, such as spin.

Background on matchgate shadows

We begin with a review of matchgate shadows. Let ${a}_{p}^{{\dagger} },{a}_{p}$ be creation and annihilation operators for a system of n fermionic modes, p ∈ [n]. The associated Majorana operators are

$${\gamma }_{2p}={a}_{p}+{a}_{p}^{{\dagger} },\quad {\gamma }_{2p+1}=-{{{\rm{i}}}}({a}_{p}-{a}_{p}^{{\dagger} }).$$

(80)

Under the Jordan–Wigner transformation¹⁰², these are mapped to Pauli operators as

$${\gamma }_{2p}=\left(\mathop{\prod}\limits_{q < p}{Z}_{q}\right){X}_{p},\quad {\gamma }_{2p+1}=\left(\mathop{\prod}\limits_{q < p}{Z}_{q}\right){Y}_{p}.$$

(81)

Recall from Eq. (2) that all d² basis operators are generated by taking arbitrary products:

$${\Gamma }_{{{{\boldsymbol{\mu }}}}}={(-{{{\rm{i}}}})}^{{m}\choose{2}}{\gamma }_{{\mu }_{1}}\cdots {\gamma }_{{\mu }_{m}},$$

(82)

where μ = (μ₁, …, μ_m) ⊆ [2n]. By convention, we order μ₁ < ⋯ < μ_m. We can group all the m-degree Majorana indices by defining the set

$${{{{\mathcal{C}}}}}_{2n,m}:=\{{{{\boldsymbol{\mu }}}}\subseteq [2n] : | {{{\boldsymbol{\mu }}}}| =m\}.$$

(83)

Physical fermionic observables have even degree m = 2k. An important subset of such operators comprises those which are diagonal in the standard basis, corresponding to the index set

$${{{{\mathcal{D}}}}}_{2n,2k}:=\{(2{p}_{1},2{p}_{1}+1,\ldots ,2{p}_{k},2{p}_{k}+1) : {{{\boldsymbol{p}}}}\in {{{{\mathcal{C}}}}}_{n,k}\}.$$

(84)

Using Eq. (81), each ${{{\boldsymbol{\tau }}}}\in {{{{\mathcal{D}}}}}_{2n,2k}$ corresponds to the Pauli-Z operator ${\Gamma }_{{{{\boldsymbol{\tau }}}}}={Z}_{{p}_{1}}\cdots {Z}_{{p}_{k}}$ under the Jordan–Wigner mapping.

The group of fermionic Gaussian unitaries is the image of the homomorphism U : O(2n) → U(d) whose adjoint action obeys

$${U}_{Q}{\gamma }_{\mu }{U}_{Q}^{{\dagger} }=\mathop{\sum}\limits_{\nu \in [2n]}{Q}_{\nu \mu }{\gamma }_{\nu },\quad Q\in {{{\rm{O}}}}(2n).$$

(85)

These unitaries are equivalent to (generalized) matchgate circuits¹²⁴ and constitute a class of classically simulatable circuits^{125,126,127,128,129,130}. Fermionic (matchgate) shadows then randomize over certain subgroups G ⊆ O(2n) of these Gaussian unitaries. The measurement channel takes the form

$${{{\mathcal{M}}}}=\mathop{\sum }\limits_{k=0}^{n}{f}_{2k}{\Pi }_{2k},$$

(86)

where the eigenvalues are

$${f}_{2k}=\left(\begin{array}{c}n\\ k\end{array}\right)\Big/\left(\begin{array}{c}2n\\ 2k\end{array}\right)$$

(87)

and each irrep is the image of

$${\Pi }_{2k}=\frac{1}{d}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{C}}}}}_{2n,2k}}\big\vert {\Gamma }_{{{{\boldsymbol{\mu }}}}}\big\rangle \!\big\rangle\!\big\langle \!\big\langle {\Gamma }_{{{{\boldsymbol{\mu }}}}}\big\vert.$$

(88)

While ${{{\mathcal{U}}}}$ carries 2n + 1 unique irreps (each labeled by a Majorana degree m)^115,124, only the n + 1 irreps λ = 2k have nonvanishing f_λ^69,70. Therefore ${{{{\mathcal{M}}}}}^{-1}$ is formally the pseudoinverse restricted to those subspaces. Finally, the shadow norm of k-body Majorana operators is⁶⁹

$$\parallel {\Gamma }_{{{{\boldsymbol{\mu }}}}}{\parallel }_{{{{\rm{shadow}}}}}^{2}={f}_{2k}^{-1}={{{\mathcal{O}}}}({n}^{k}).$$

(89)

Variance expressions for arbitrary observables can be found in refs. ^70,71. For the postprocessing of T shadows into estimates of all k-body Majorana observables, we describe an algorithm in Supplementary Note 5 which runs in time ${{{\mathcal{O}}}}({n}^{k}T)$.

We now comment on the choice of G ⊆ O(2n). Fermionic classical shadows were introduced in ref. ⁶⁹, which initially considered the intersection of proper matchgate circuits [the special orthogonal group SO(2n)] with n-qubit Clifford unitaries Cl(n). The result is the group of all 2n × 2n signed permutation matrices with determinant 1, denoted by B⁺(2n) ⊂ SO(2n). They also showed that its unsigned subgroup, Alt(2n) ⊂ B⁺(2n), possesses the same irrep structure [ref. ⁶⁹, Supplemental Material, Theorem 11]. While the full, continuous group SO(2n) has not yet been analyzed for classical shadows, it was studied for character randomized benchmarking¹¹⁴ in [ref. ¹¹⁵, Sec. VI], wherein they demonstrated the presence of multiplicities. These multiplicities can be avoided by enlarging to the generalized matchgate group, i.e., all of O(2n) [ref. ¹²⁴, Lemma 3]. Ref. ⁷⁰ applied these generalized matchgates to fermionic classical shadows, and in particular they prove that the Clifford intersection in this setting (now yielding the subgroup B(2n) ⊂ O(2n) of signed permutation matrices with either determinant ±1) is a 3-design for O(2n). This implies that B(2n) is also multiplicity-free.

Due to the variety of options, for the rest of this paper we assume matchgate shadows under any G with the desired irreps. We note that ref. ⁷¹ introduced a smaller subset of B(2n) based on perfect matchings, which has the same channel ${{{\mathcal{M}}}}$ and variances; however, its connection to representation theory was not explored.

Utilizing particle-number symmetry

Suppose the ideal state we wish to prepare lies in the η-particle sector of ${{{\mathcal{H}}}}$. This is a U(1) symmetry generated by the fermion-number operator, $N={\sum }_{p\in [n]}{a}_{p}^{{\dagger} }{a}_{p}$. In particular, powers of N obey

$${{{\rm{tr}}}}({N}^{k}\rho )={\eta }^{k},$$

(90)

which provides us a collection of conserved quantities with which to perform symmetry adjustment. Recall from Eq. (88) that Π_m projects onto the irrep

$${V}_{m}={{{\rm{span}}}}\{{\Gamma }_{{{{\boldsymbol{\mu }}}}} : {{{\boldsymbol{\mu }}}}\in {{{{\mathcal{C}}}}}_{2n,m}\}.$$

(91)

Then, projecting N^k onto V_2k yields the symmetry operators S_2k, and solving the resulting linear system of equations recovers the ideal values for ${s}_{2k}={{{\rm{tr}}}}({S}_{2k}\rho )$. For ease of exposition we will consider only k = 1, 2, but one may generalize to higher k using these ideas.

Concretely, we start with the fact that ${a}_{p}^{{\dagger} }{a}_{p}=({\mathbb{I}}-{\Gamma }_{(2p,2p+1)})/2$, and Γ_(2p, 2p+1)Γ_(2q, 2q+1) = Γ_{(2p, 2p+1, 2q, 2q+1)} for p < q. Then, expanding N and N² into a linear combination of Majorana operators, one finds

$${S}_{2}={\Pi }_{2}(N)=-\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{D}}}}}_{2n,2}}{\Gamma }_{{{{\boldsymbol{\mu }}}}},$$

(92)

$${S}_{4}={\Pi }_{4}({N}^{2})=\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{D}}}}}_{2n,4}}{\Gamma }_{{{{\boldsymbol{\mu }}}}}.$$

(93)

Using Eq. (90) and the relations between S₂ and S₄ to N and N² (for example, $N=n{\mathbb{I}}/2+{S}_{2}$), we arrive at:

$${s}_{2}={{{\rm{tr}}}}\left({S}_{2}\rho \right)=\eta -\frac{n}{2},$$

(94)

$${s}_{4}={{{\rm{tr}}}}\left({S}_{4}\rho \right)=\frac{1}{2}\left(\begin{array}{c}n\\ 2\end{array}\right)-\eta (n-\eta ).$$

(95)

For the sampling cost incurred by these symmetry operators, we argue that the typical shadow norms of these symmetries are $\parallel {S}_{2k}/{s}_{2k}{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}({n}^{k})$, which is the same as the base estimation. To see this, consider a triangle inequality on the shadow norm:

$$\begin{array}{lll}\parallel {S}_{2k}{\parallel }_{{{{\rm{shadow}}}}}\,\le \,\displaystyle{\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{D}}}}}_{2n,2k}}{\parallel} {\Gamma }_{{{{\boldsymbol{\mu }}}}}{\parallel }_{{{{\rm{shadow}}}}}}\\ \qquad\qquad\quad\;\;=\,\displaystyle{\frac{1}{2}\left(\begin{array}{c}n\\ k\end{array}\right)\sqrt{\left(\begin{array}{c}2n\\ 2k\end{array}\right)\Big/\left(\begin{array}{c}n\\ k\end{array}\right)}}\\ \qquad\qquad\quad\;\;=\,{{{\mathcal{O}}}}({n}^{3k/2}).\end{array}$$

(96)

Thus $\parallel {S}_{2}{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}({n}^{3})$ and $\parallel {S}_{4}{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}({n}^{6})$. Next, we need to examine how ${s}_{2k}^{2}$ scales with system size. Assuming that s₂, s₄ ≠ 0 and that the number of electrons is $\eta ={{{\mathcal{O}}}}(n)$, then from Eqs. (94) and (95) we see that ${s}_{2}^{2}=\Theta ({n}^{2})$ and ${s}_{4}^{2}=\Theta ({n}^{4})$. Thus

$$\parallel {S}_{2}/{s}_{2}{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}(n),$$

(97)

$$\parallel {S}_{4}/{s}_{4}{\parallel }_{{{{\rm{shadow}}}}}^{2}={{{\mathcal{O}}}}({n}^{2}).$$

(98)

Avoiding division by zero

One potential obstruction to symmetry adjustment is when some s_2k = 0. This can occur whenever the particle number takes a specific value:

$${s}_{2}=0\,{{{\rm{if}}}}\,\eta =\frac{n}{2},$$

(99)

$${s}_{4}=0\,{{{\rm{if}}}}\,\eta =\frac{n\pm \sqrt{n}}{2}.$$

(100)

Equation (99) occurs at half-filling, which is fairly common. On the other hand, Eq. (100) occurs only when the number of modes n is a perfect square and the number of particles η is one of two specific values, so it is less likely to occur. Nonetheless, there is a straightforward way to circumvent both possibilities by introducing a single ancilla qubit.

To do so, append an additional fermion mode initialized in the unoccupied state $\left\vert 0\right\rangle$, so that the ideal state is now the (n + 1)-mode state ${\rho }^{{\prime} }=\rho \otimes \left\vert 0\right\rangle \!\left\langle 0\right\vert$. Given that ρ has η particles on n modes, ${\rho }^{{\prime} }$ is an η-particle state on n + 1 modes. The new symmetry operators on the (n + 1)-mode Hilbert space are

$${S}_{2}^{{\prime} }=-\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{D}}}}}_{2(n+1),2}}{\Gamma }_{{{{\boldsymbol{\mu }}}}},$$

(101)

$${S}_{4}^{{\prime} }=\frac{1}{2}\mathop{\sum}\limits_{{{{\boldsymbol{\mu }}}}\in {{{{\mathcal{D}}}}}_{2(n+1),4}}{\Gamma }_{{{{\boldsymbol{\mu }}}}},$$

(102)

which have ideal values

$${s}_{2}^{{\prime} }={{{\rm{tr}}}}\left({S}_{2}{\rho }^{{\prime} }\right)=\eta -\frac{n+1}{2},$$

(103)

$${s}_{4}^{{\prime} }={{{\rm{tr}}}}\left({S}_{4}{\rho }^{{\prime} }\right)=\frac{1}{2}\left(\begin{array}{c}n+1\\ 2\end{array}\right)-\eta (n+1-\eta ).$$

(104)

It is straightforward to check that, if either condition Eq. (99) or Eq. (100) holds, then ${s}_{2}^{{\prime} }$ and ${s}_{4}^{{\prime} }$ are always nonzero for n > 1.

Under the Jordan–Wigner mapping, this modification is easily achieved by initializing a single ancilla qubit in $\left\vert 0\right\rangle$. Recall that the terms in the symmetries S₂, S₄ are the diagonal operators Γ_(2p, 2p+1) = Z_p and Γ_{(2p, 2p+1, 2q, 2q+1)} = Z_pZ_q. Note also that the ancilla qubit is acted on only during the random unitary U_Q (where now Q has dimension 2n + 2) and otherwise does not interact with the n system qubits.

Application to qubit (Pauli) shadows

Now we turn to the application for local observable estimation in systems of spin-1/2 particles (qubits). Random Pauli measurements are efficient for this task; however, for compatibility with the global U(1) symmetry considered in this work, we must slightly modify the protocol to accommodate its irreps. We begin with a review of the standard Pauli shadows protocol, followed by our modification.

Background on standard Pauli shadows

The local Clifford group Cl(1)^⊗n is implemented by uniformly drawing a single-qubit Clifford gate for each qubit independently. It has 2ⁿ irreducible representations, corresponding to all k-qubit subsystems I ⊆ [n], where ∣I∣ = k ∈ {0, 1, …, n}¹³¹. Twirling ${{{{\mathcal{M}}}}}_{Z}$ by this group yields

$${{{\mathcal{M}}}}=\mathop{\sum}\limits_{I\subseteq [n]}{f}_{I}{\Pi }_{I},$$

(105)

where f_I = 3^−∣I∣ and Π_I projects onto the subspace of operators which act nontrivially on precisely the subsystem I. The squared shadow norm for k-local Pauli operators P is⁵¹

$$\parallel P{\parallel }_{{{{\rm{shadow}}}}}^{2}={3}^{k}.$$

(106)

A more general variance bound was derived in ref. ⁵²: a simple loose bound of their result can be stated as ${{{\rm{Var}}}}[\hat{o}]\le {3}^{k}R{\parallel} O{\parallel }_{\infty }^{2}$, where O is an arbitrary k-local traceless observable and R is the number of terms in its Pauli decomposition. However, they argue that a tighter expression, essentially ${3}^{k}{\parallel} O{\parallel }_{\infty }^{2}$, is typically a good approximation to the variance.

Subsystem symmetrization of Pauli shadows

The irreps of Cl(1)^⊗n are difficult to reconcile with commonly encountered symmetries. For example, consider a conserved total magnetization M = ∑_i∈[n]Z_i. In terms of qubits, this is equivalent to the different Hamming-weight sectors. Each term Z_i lies in a different irrep I = {i}, so M spans multiple irreps rather than having a single conserved quantity per irrep.

To remedy this conflict, we introduce what we call subsystem-symmetrized Pauli shadows, which randomizes over a group whose irreps are labeled only by the qubit locality k, rather than any specific subsystem I of k qubits. (This is analogous to how the matchgate irreps depend only on fermionic locality, due to the inherent antisymmetry of fermions.) We formalize the group as follows.

Definition 5

The subsystem-symmetrized local Clifford group is defined as ${{{\rm{Cl}}}}{(1)}_{{{{\rm{Sym}}}}}^{\otimes n}:={{{\rm{Sym}}}}(n)\times {{{\rm{Cl}}}}{(1)}^{\otimes n}$, where Sym(n) is the symmetric group and Cl(1) is the single-qubit Clifford group. Its unitary action on ${{{\mathcal{H}}}}$ is given by

$${U}_{(\pi ,C)}={S}_{\pi }C,$$

(107)

where C = ⨂_i∈[n]C_i ∈ Cl(1)^⊗n and π ∈ Sym(n) is represented by a permutation of the n qubits:

$${S}_{\pi }\vert {b}_{0}\rangle \cdots \vert {b}_{n-1}\rangle =\vert {b}_{{\pi }^{-1}(0)}\rangle \cdots \vert {b}_{{\pi }^{-1}(n-1)}\rangle$$

(108)

for all b_i ∈ {0, 1}, i ∈ [n].

The unitaries S_π can be implemented with ${{{\mathcal{O}}}}({n}^{2})$ gates and depth ${{{\mathcal{O}}}}(n)$, for example by constructing a parallelized network of nearest-neighbor SWAP gates according to an odd–even sorting algorithm⁹⁹ applied to π. Representing π as an array of the permuted elements of [n], the sorting algorithm returns a sequence of adjacent transpositions i ↔ i + 1 which maps π to (0, 1, …, n − 1). This sequence therefore implements π⁻¹ as desired. Each such transposition then maps to a SWAP_i,i+1 gate to construct the quantum circuit. For the postprocessing of T shadows into k-local Pauli estimates, we review in Supplementary Note 5 the algorithm which runs in time ${{{\mathcal{O}}}}({n}^{k}T)$.

We prove the relevant properties of subsystem-symmetrized Pauli shadows in Supplementary Note 2, namely its irreps and the shadow norm of local observables. We summarize the results here: each irrep is the space of all k-local operators,

$${V}_{k}={{{\rm{span}}}}({{{{\mathcal{B}}}}}_{k})\,{{{\rm{where}}}}\,{{{{\mathcal{B}}}}}_{k}:=\{P\in {{{\mathcal{P}}}}(n):| P| =k\},$$

(109)

for each k ∈ {0, 1, …, n}. Hence the (noisy) measurement channel is

$$\widetilde{{{{\mathcal{M}}}}}=\mathop{\sum }\limits_{k=0}^{n}{\widetilde{f}}_{k}{\Pi }_{k},$$

(110)

where ${\widetilde{f}}_{k}={{{\rm{tr}}}}({{{{\mathcal{M}}}}}_{Z}{{{\mathcal{E}}}}{\Pi }_{k})/\left({3}^{k}\left(\begin{array}{c}n\\ k\end{array}\right)\right)$ and

$${\Pi }_{k}=\frac{1}{d}\mathop{\sum}\limits_{P\in {{{{\mathcal{B}}}}}_{k}}\left.\left\vert P\right\rangle \!\right\rangle \!\left\langle \!\left\langle P\right\vert \right..$$

(111)

When ${{{\mathcal{E}}}}$ is the identity channel, we recover f_k = 3^−k. Also in the absence of noise, the variance formulas are exactly the same as in standard Pauli shadows.

The canonical example we have considered in this paper is a U(1) symmetry generated by a total magnetization M = ∑_i∈[n]Z_i. Suppose the ideal state has a known value of $m={{{\rm{tr}}}}(M\rho )$ (equivalently, ρ lives in a sector of fixed Hamming weight (n − m)/2). The symmetries projected into the irreps of ${{{\rm{Cl}}}}{(1)}_{{{{\rm{Sym}}}}}^{\otimes n}$ are then

$${S}_{1}={\Pi }_{1}(M)=\mathop{\sum}\limits_{i\in [n]}{Z}_{i},$$

(112)

$${S}_{2}={\Pi }_{2}({M}^{2})=2\mathop{\sum}\limits_{i < j}{Z}_{i}{Z}_{j},$$

(113)

whose ideal values are

$${s}_{1}=m,$$

(114)

$${s}_{2}={m}^{2}-n.$$

(115)

As in the fermionic setting, we encounter issues if s₁ or s₂ vanish (i.e., m = 0 or $m=\pm \sqrt{n}$, respectively). In this case, we can perform the same ancilla trick, appending a qubit in $\left\vert 0\right\rangle$ and modifying the conserved quantities to

$${s}_{1}^{{\prime} }=m+1,$$

(116)

$${s}_{2}^{{\prime} }={(m+1)}^{2}-(n+1).$$

(117)

The variances of the symmetry operators are

$${{{\rm{Var}}}}[{\hat{s}}_{1}/{s}_{1}]={{{\mathcal{O}}}}(n),$$

(118)

$${{{\rm{Var}}}}[{\hat{s}}_{2}/{s}_{2}]={{{\mathcal{O}}}}(1),$$

(119)

whenever the ideal state lives in a symmetry sector of constant m = Θ(1). We show this in Supplementary Note 2, along with general m-dependent expressions. This n-dependent variance bound reflects the fact that the symmetries are extensive properties. While local Pauli operators have variances bounded by a constant, we point out that many local observables of interest are linear combinations of an extensive number of Pauli terms. As such, their shadow norms typically grow with system size as well (which can also be seen by the fact that the shadow norm scales with operator norm).