Introduction

Si/SiGe quantum dots are an attractive platform for quantum computation1,2,3, as demonstrated by recent experiments4,5,6 where both single and two-qubit gate fidelities have exceeded the error correction threshold of 99%7. However, Si/SiGe quantum dots suffer from small energy spacings between the ground and excited valley states8, called valley splittings, EVS, which induce leakage if they are small9. Popular strategies for enhancing EVS include engineering atomically sharp interfaces10,11,12 or narrow quantum wells13,14. Unfortunately, random-alloy disorder13 causes EVS to vary significantly from dot to dot14,15, with typical values ranging from 20 to 300 μeV16,17,18,19,20,21,22,23,24.

The Wiggle Well (WW) has recently emerged as an important tool for enhancing the valley splitting, by adding Ge concentration oscillations ("wiggles”) of wavelength λ to the Si quantum well25. Theoretical estimates suggest that these wiggles could provide a remarkable boost of EVS ≈ 1 meV for an average Ge concentration of only \({\bar{n}}_{{{{\rm{Ge}}}}}=1 \%\)26. However, the small wavelength needed for this structure (λ = 0.32 nm) corresponds to roughly two atomic monolayers, suggesting that such growth would be very challenging. Naive band-structure estimates also identify a second, longer λ, that could produce a large EVS by coupling valleys in neighboring Brillouin zones. However, rigorous calculations26 show that this coupling is inhibited by the nonsymmorphic screw symmetry of the Si crystal27.

In this work, we show that a modified structure called a strain-assisted Wiggle Well (STRAWW) can overcome these problems. This device combines a long-wavelength WW (λ ≈ 1.7 nm), which has already been demonstrated in the laboratory25, with an experimentally feasible level of shear strain. We further show that valley splitting in STRAWW is largely independent of both the vertical electric field and the interface sharpness, thus simplifying heterostructure growth. We also note that the long-wavelength WW has a much larger spin-orbit coupling than conventional Si/SiGe quantum wells27, even in the absence of shear strain, which enables fast spin manipulation via electric dipole spin resonance (EDSR), without requiring a micromagnet. This combination of large valley splitting and large spin-orbit coupling makes STRAWW a very attractive platform for Si spin qubits. Below, we first provide an overview of the physics and implementation of strain in the STRAWW proposal, and then present calculations showing deterministically enhanced valley splittings.

Results

Valley splitting enhancement mechanism

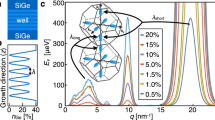
Shear strain has a subtle but profound effect on the silicon crystal lattice shown in Fig. 1a. In Fig. 1b, we also show an effective 1D lattice obtained by assuming translational symmetry along \(\hat{x}\) and \(\hat{y}\) and performing a Fourier transformation. (This 1D model forms the starting point for the effective-mass theory described below.) The conventional primitive unit cell of Si contains two atoms (red and blue), which give rise to the two sublattices shown in the figure. Now, for the special case of kx = ky = 0, silicon possesses a screw symmetry, which interchanges the red and blue lattices, and reduces the primitive cell to one atom27. Note that the weak in-plane confinement of a quantum dot has an insignificant effect on the valley coupling described here, justifying the focus on kx = ky = 0. The Brillouin zone along \({\hat{k}}_{z}\) can then be expanded from kz = ± 2π/a0 to ± 4π/a0, as shown in Fig. 1c. Here a0 is the size of the cubic unit cell, and the low-energy valley minima are located at kz = ± k0. In the absence of valley coupling, each state from the − k0 valley will have a degenerate partner from the k0 valley, as shown in the left-hand side of Fig. 1d. Hence, a coupling between these valleys is needed for a valley splitting EV S between the two lowest energy states to exist. A short-period WW—if it could be grown—would provide a direct (i.e., first-order) 2k0 coupling between the valleys, by introducing ultrashort-period Ge concentration oscillations into the quantum well (Fig. 1k), with λ = 2π/(2k0)25,26. Here, we propose a more physically realistic, second-order coupling scheme involving (i) shear strain, which couples kz states separated by 4π/a0 (green arrow in Fig. 1c), and (ii) a long-period WW of wavelength λ = 2π/(2k1) (blue arrow in Fig. 1c).

Fig. 1: Strain-assisted Wiggle Well (STRAWW) proposal.
figure 1

a Unstrained silicon cubic unit cell of length a0, composed of two sublattices (red and blue). In the absence of strain, the sublattices are interchanged by a screw-symmetry operation. b Assuming periodicity in the crystallographic [100] and [010] directions, the three dimensional (3D) lattice can be reduced to an effective 1D lattice27, whose primitive unit cell length is given by a0/4, due to the screw symmetry. c Low-energy Si band structure for the 1D lattice, expressed in a Brillouin zone (BZ) of length 8π/a0 along the [001] reciprocal axis kz. The 2k0 valley coupling is achieved in two steps: (i) a 4π/a0 coupling induced by shear strain; (ii) a 2k1 coupling provided by the Wiggle Well. d In the absence of valley coupling (left side), the states are two-fold degenerate due to the two-fold valley degeneracy in (c). Valley coupling breaks this degeneracy (right side), leading to a valley splitting EVS. e Projection of the unstrained cubic unit cell onto the x–y plane. f Schematic deformation of the unit cell under shear strain along [110]. g Silicon tetrahedral bonds in the absence of strain. h Shear strain affects bonds differently, depending on the crystal plane, causing a lattice deformation along [001]. i, Shear strain reduces the translation symmetry of the 1D lattice, resulting in a primitive unit cell of length a0/2. j The corresponding BZ is then folded in half, and the shear-strain coupling kz = 4π/a0 is manifested as avoided crossings at the BZ boundary. Here, the green and blue arrows correspond to the same arrows in c, and the two black dots denote equivalent kz separated by a reciprocal lattice vector 4π/a0. Notice that the shear strain coupling (green arrow) conserves momentum in the reduced BZ. (c and j are both calculated using the sp3d5s* tight-binding model described in Methods.) k Typical Ge concentration profile of a Wiggle Well heterostructure25,26. Here, the Ge oscillation wavelength, λ = π/k1 ≈ 1.68 nm, is chosen to couple the valleys, as in (c. l, m), Cartoon depiction of shear strain (εxy) in a quantum well, before (l) and after (m) mechanical bending. Cartoon depiction of shear strain induced by lithographic etching, before (n) and after (o) lattice deformation caused by cooling to cryogenic temperatures.

Full size image

The mechanism responsible for the strain-induced 4π/a0 coupling is illustrated in Fig. 1e–h. Here, shear strain εxy is seen to elongate and compress the crystal along the [110] and \([1\bar{1}0]\) directions, respectively. In turn, this distorts the tetrahedral bonds of the diamond lattice and shifts the blue sublattice downward with respect to the red sublattice (along \([00\bar{1}]\)), as shown in Fig. 1h, i. This layer pairing causes the primitive cell to expand from one to two atoms, and the BZ folds back to the conventional boundaries at kz = ± 2π/a0 (Fig. 1j). The period of the distortion is a0/2, which gives the desired 4π/a0 coupling vector upon Fourier transformation, and produces an avoided crossing of the low-energy bands, as observed at the zone boundary. We note that the coupling responsible for this avoided crossing is the same as the green arrow in Fig. 1j, except it occurs between states at kz = ± 2π/a0 instead of ± k0.

The second-order process illustrated in Fig. 1c couples the two valleys through a virtual (i.e., high-energy) state, indicated by a black dot. The resulting momentum loop can be expressed as 2k1 = 4π/a0 − 2k0, where the Ge concentration period λ = π/k1 ≈ 1.68 nm corresponds precisely to the long-wavelength WW. We note that this period is 5.3 times larger than the period for the short-wavelength WW26, making it experimentally feasible25. We also note that such large strains are commonly employed in the microelectronics industry28,29, where they are used to improve transistor performance. In the laboratory, we envision implementing shear strain through simple mechanical deformations, like those illustrated in Fig. 1l and m, for near-term experiments. In the long term, scalable solutions will likely involve etched geometries, like those illustrated in Fig. 1n, o, or other stressor-based strategies used in industry. Below, we simulate several shear-strain geometries that could be implemented in experiments, obtaining strain levels sufficient for achieving deterministically enhanced valley splittings greater than 100 μeV. These results indicate that the STRAWW proposal is feasible and can be achieved with existing technology.

sp3d5s* tight-binding calculations

We now perform numerical simulations to quantify the effects of shear strain and Ge oscillations on the valley splitting, finding that significant enhancements are observed only when both features are present. We begin by employing an sp3d5s* tight-binding model30,31, which is known to give accurate results for the band structure over a wide range of energies (see Methods). The model incorporates tight-binding parameters for Si-Si, Ge-Ge, and Si-Ge nearest-neighbor hoppings, and can therefore describe arbitrary Si1−xGex alloys. The model also includes strain, yielding results that are in good agreement with experimentally measured deformation potentials30. Here, we focus on the deterministic component of EVS, ignoring local fluctuations of the Ge concentration13. The SiGe alloy is therefore treated in a virtual crystal approximation, following ref. 27, where the Hamiltonian matrix elements are averaged over all possible alloy realizations.

In Fig. 2, we plot the valley splitting EVS as a function of the shear strain εxy and the average Ge concentration in the quantum well \({\bar{n}}_{{{{\rm{Ge}}}}}\). We consider a uniform vertical electric field of strength Fz = 2 mV/nm and the optimal STRAWW oscillation wavelength of λ = 1.68 nm. We also assume a wide interface of width w = 1.9 nm, as defined in Methods, which strongly suppresses the interface-induced valley splitting13 and ensures that the valley splitting enhancements we observe here are caused by the STRAWW structure. Figure 2a shows results in the two-dimensional parameter space, while Fig. 2b shows two vertical linecuts, and Fig. 2c shows two horizontal linecuts, including the cases with εxy = 0 or \({\bar{n}}_{{{{\rm{Ge}}}}}=0\). These results clearly indicate that a combination of shear strain and concentration oscillations is needed to produce a large valley splitting. Indeed, when εxy = 0 or \({\bar{n}}_{{{{\rm{Ge}}}}}=0\), we observe dangerously low values of EVS < 25 μeV, over the whole parameter range. In contrast, when both \({\varepsilon }_{xy},{\bar{n}}_{{{{\rm{Ge}}}}} \,>\, 0\), we quickly approach a range of acceptable valley splittings. For example, when εxy = 0.15% and \({\bar{n}}_{{{{\rm{Ge}}}}}=2.5 \%\) (black star in Fig. 2a), we obtain EVS ≈ 125 μeV.

Fig. 2: Enhanced valley splitting.
figure 2

a Valley splitting as function of shear strain and Ge concentration at the optimal WW wavelength λ = 1.68 nm, computed using sp3d5s* tight-binding theory. Here we assume a wide interface, w = 1.9 nm, and electric field, Fz = 2 mV/nm. (Black star refers to Fig. 3). b Line cuts from (a), corresponding to εxy = 0 (dashed line) and 0.15% (solid line). c Line cuts from (a), corresponding to \({\bar{n}}_{{{{\rm{Ge}}}}}=0\) (dashed line) and 2.5% (solid line). Only the combination of shear strain and WW is found to significantly enhance the valley splitting.

Full size image

In Fig. 3, we show that the valley splitting enhancements observed in Fig. 2 are robust to imperfect implementation of the STRAWW wavelength λ = 1.68 nm. Plotting EVS as a function of λ and \({\bar{n}}_{{{{\rm{Ge}}}}}\) in Fig. 3a, or εxy in Fig. 3b, we find that a broad range of λ values gives acceptable valley splittings. For example, at the physically realistic device setting indicated by a black star (the same setting as Fig. 2), we obtain EVS ≈ 125 μeV; on either side of this point, the range of wavelengths with EVS > 100 μeV extends from λ = 1.5–1.9 nm, which is well within the growth tolerance achieved in ref. 25. Finally, we note that, near the optimal wavelength λ = 1.68 nm, EVS varies linearly with both \({\bar{n}}_{{{{\rm{Ge}}}}}\) and εxy, which we now explain using effective-mass theory.

Fig. 3: Robustness of STRAWW to λ errors.
figure 3

Valley splitting as a function of the Ge oscillation wavelength λ, for fixed values of (a), εxy = 0.15%, or (b), \({\bar{n}}_{{{{\rm{Ge}}}}}=2.5 \%\). For realistic device parameters (e.g., the black stars, referring to Fig. 2), acceptable valley splittings are achieved over a wide range of λ, providing robustness against growth imperfection.

Full size image

Effective mass theory

To gain further insight into the separate (or combined) contributions to the valley splitting from shear strain and Ge concentration oscillations, we outline here an effective-mass theory, with details given in Supplementary Note 132. This formalism provides intuition regarding valley-splitting enhancement mechanisms arising from Ge concentration oscillations and shear strain, while also being amenable to analytic analysis. Treating the valleys centered at kz = ± k0 as pseudospins, the Hamiltonian takes the form

$${H}_{{{{\rm{EM}}}}}=\left(\begin{array}{cc}{H}_{0}&{H}_{v}\\ {H}_{v}^{{\dagger} }&{H}_{0}\end{array}\right),$$
(1)

where H0 is the intra-valley Hamiltonian and Hv describes the inter-valley couplings. The intra-valley Hamiltonian is given by

$${H}_{0}=-\frac{{\hslash }^{2}}{2{m}_{l}}{\partial }_{z}^{2}+V(z),$$
(2)

where ml = 0.92me is the longitudinal effective mass, and

$$V(z)={V}_{0}\cos \left(\frac{2\pi z}{\lambda }\right)+{V}_{{{{\rm{qw}}}}}(z),$$
(3)

where the first term describes potential modulations of amplitude V0 due to the Ge oscillations, and Vqw describes both the quantum-well confinement potential and the applied electric field. The inter-valley Hamiltonian takes the form

$$\begin{array}{ll}{H}_{v}\,=\,V(z){e}^{-i2{k}_{0}z}-i{\varepsilon }_{xy}{e}^{i2{k}_{1}z}\left[{C}_{1}+{C}_{2}(i2{k}_{1}\,{\partial }_{z}+{\partial }_{z}^{2})\right],\end{array}$$
(4)

where C1 = 1.73 eV and \({C}_{2}=0.067{a}_{0}^{2}{C}_{1}\) are constants, and C1 is adjusted to match the valley splitting results from our sp3d5s* calculations. It is interesting to see two types of “fast” oscillations in this equation (indicated in Fig. 1c), with wavevectors 2k0 arising from the potential, and 2k1 arising from the shear strain.

We solve for the low-energy states of Eq. (1) using an envelope function method similar to ref. 33 (see also Methods) by treating V0 and C1εxy perturbatively. Defining ψ as the ground state of H0 in Eq. (2), this analysis yields a simple but extremely useful expression for the inter-valley matrix element, Δ = 〈ψ∣Hv∣ψ〉:

$$\begin{array}{lll}\Delta &=& \displaystyle\int\,| {F}_{0}(z){| }^{2}\bigg[{V}_{{{{\rm{qw}}}}}(z){e}^{-i2{k}_{0}z}+\frac{{V}_{0}}{2}{e}^{-i(2{k}_{0}-{G}_{\lambda })z}\\&&-\, i{\varepsilon }_{xy}{C}_{1}{e}^{i2{k}_{1}z}-i{\varepsilon }_{xy}\frac{{V}_{0}}{{E}_{\lambda }}\left({C}_{1}-{C}_{2}{k}_{1}{G}_{\lambda }\right){e}^{i(2{k}_{1}-{G}_{\lambda })z}\bigg]\,dz,\end{array}$$
(5)

where F0(z) is the envelope function of ψ(z) (obtained by setting V0 = 0), and we have defined the oscillation wavevector and oscillation energy scales as Gλ = 2π/λ and Eλ = 2ℏ2π2/(mlλ2), respectively. Note here that EVS = 2∣Δ∣.

Each of the four terms in Eq. (5) effectively averages to zero for smoothly varying F0 and Vqw, except when specific resonance conditions are met, and each term has a distinct physical origin and meaning, as explained below. The first term is the usual inter-valley matrix element in the absence of Ge oscillations and shear strain13. The second term describes Ge oscillations, independent of shear strain, and is the basis for the short-wavelength WW25,26. The third term describes the shear strain contribution, independent of Ge oscillations. The fourth term involves both shear strain and Ge oscillations, and is unique to STRAWW. The resonance condition for which this term has a vanishing exponential, 2k1 ≈ Gλ, corresponds to the long-period WW, or λ = π/k1 ≈ 1.68 nm.

We can evaluate Eq. (5) for a specific quantum well model. For simplicity, we treat the quantum well as a harmonic confining potential with \({V}_{{{{\rm{qw}}}}}={m}_{l}{\omega }_{z}^{2}{z}^{2}/2\), and the envelope function \({F}_{0}(z)={(\pi {l}_{z}^{2})}^{-1/4}\exp ({z}^{2}/(2{l}_{z}^{2}))\), where \({l}_{z}=\sqrt{\hslash /({m}_{l}{\omega }_{z})}\) is the characteristic dot size in the growth direction. Equation (5) then reduces to

$$\begin{array}{ll}\Delta\,=\,\frac{{\hslash }^{2}{k}_{0}^{2}}{2{m}_{l}}{e}^{-{({k}_{0}{l}_{z})}^{2}}+\frac{{V}_{0}}{2}{e}^{-{(2{k}_{0}-{G}_{\lambda })}^{2}{l}_{z}^{2}/4}\\\quad-i{\varepsilon }_{xy}{C}_{1}{e}^{-{({k}_{1}{l}_{z})}^{2}}-i{\varepsilon }_{xy}({C}_{1}-{C}_{2}{k}_{1}{G}_{\lambda })\frac{{V}_{0}}{{E}_{\lambda }}{e}^{-{(2{k}_{1}-{G}_{\lambda })}^{2}{l}_{z}^{2}/4}.\end{array}$$
(6)

If we now assume a long-period WW, with 2k1 = Gλ, the first three terms in Eq. (6) are all exponentially suppressed, leaving \({E}_{\rm{VS}}\; \,\approx\, (2{\varepsilon }_{xy}{V}_{0}/{E}_{\lambda })({C}_{1}-2{C}_{2}{k}_{1}^{2})\). This confirms the anticipated linear dependence on εxy and V0, and provides a simple estimate for the STRAWW valley splitting. We also note that this expression is independent of lz, justifying our approximate treatment of the quantum well-confining potential, and indicating that the valley splitting does not depend on the interface for this smooth quantum-well geometry.

In the opposite limit of an ultra-sharp interface, Eq. (6) is no longer accurate. In this case, the singular nature of the confining potential Vqw (or the envelope function F0) generates Fourier components that cancel out the fast-oscillating phase factors in Eq. (5), so the first three terms are not suppressed. The resulting valley splitting enhancement has been studied previously for quantum wells with34,35,36 and without13 shear strain. However in the latter case, the crossover between ultra-sharp vs smooth interfaces occurs for interface widths of just 1–2 atomic monolayers, which are extremely difficult to grow in the laboratory15, so valley splitting enhancements are rarely observed. In Supplementary Note 232, we show numerically that the same is true for shear-strained structures, suggesting that the STRAWW strategy is much more practical.

Strain calculations

Finally, we show that the shear strains needed to deterministically enhance the valley splitting can be achieved with current micro and nanofabrication technologies. In Fig. 4, we consider two etching strategies. Figure 4a shows a microbridge geometry37,38, formed by etching the top surface to well below the quantum well. Here, the trenches are aligned along the [110] crystallographic direction to provide shear strain in the channel region between the trenches. We calculate the strain in the quantum well numerically, using COMSOL Multiphysics39, for the geometry shown in Fig. 4a, with L = W = d = 1 μm. The resulting shear strain εxy shown in Fig. 4b is largely uniform across the channel, except for edge strips with an approximate width of 100 nm. At the center of the channel, we obtain εxy ≈ − 0.1%, which yields a large EVS, even for a moderate WW amplitude (see Fig. 2). In this geometry, the trenches are sufficiently separated to allow for electrode fabrication using the realistic design shown in Fig. 4c. This design has geometric parameters comparable to ref. 24 in the dot region, and here we exploit the large amount of free space in the orthogonal direction to fan out the gates, to avoid forming sharp kinks that could lead to lithographic failure. To allow for a higher density of gate electrodes, we envision filling the trenches with an oxide material, to restore a planar top surface on which additional gates can be fabricated.

Fig. 4: Strategies for implementing shear strain.
figure 4

a Microbridge geometry of dimension L × W, defined by two trenches of depth d etched into the top of a Si/SiGe heterostructure along the [110] direction. b Calculated shear strain εxy in the quantum well, for the geometry defined by L = W = d = 1μm. A large shear strain, εxy ≈ − 0.1%, is obtained in the center of the channel. c A triple-dot gate design, analogous to ref. 24, with gates arranged to avoid the trenches, for the same geometry as (b). d A 3D membrane-stressor geometry, with (e), a corresponding [110] cross-section. A free-standing membrane is formed by etching a trench, with lateral dimensions L1 × L2, from the bottom of a Si substrate to a buried oxide (BOX) etch stop. A Si3N4 stressor of dimension w1 × w2 is fabricated atop the Si/SiGe quantum well. The stressor is centered above one trench edge, such that it partially covers the membrane. Both membrane and stressor are aligned along [110]. f Calculated shear strain in the quantum well, for the geometry defined by (L1, L2, w1, w2) = (50, 100, 50, 100) μm, where the membrane and stressor regions are outlined by dashed and solid lines, respectively. The membrane deforms oppositely, depending on whether it is covered or uncovered by the stressor. Relatively uniform strain is achieved across the wide, blue region, with εxy = 0.15% at the location of the orange star.

Full size image

Figure 4d, e shows a second, stressor-type geometry, featuring a Si/SiGe heterostructure grown atop a buried oxide (BOX) layer40, which serves as an etch-stop for a trench etched from the bottom of the Si substrate. The latter is aligned along [110], creating a free-standing Si/SiGe membrane41,42, which is readily strained by a Si3N4 stressor43,44,45 (also aligned along [110]), due to the thinness of the membrane. For the geometry defined by (L1, L2, w1, w2) = (50, 100, 50, 100) μm, we obtain the strain results shown in Fig. 4f, where we assume a depositional tensile stress of 1 GPa for the Si3N4 stressor43. Here, the red region is covered by stressor, while the blue region is uncovered, but located above the trench. This blue region, which is most convenient for fabricating gates, provides a high and largely uniform shear strain, with εxy ≈ 0.15% at the location of the orange star, and εxy ≥ 0.15% over a wide area (>785 μm2) that could potentially contain many dots in a dense two-dimensional array46,47,48,49.

Discussion

In summary, we have shown that the combination of shear strain and the long-period Wiggle Well, dubbed “STRAWW,” is particularly effective for deterministically enhancing the valley splitting, which is a key missing ingredient for scaling up silicon spin qubits to large arrays. Effective-mass theory shows that this enhancement arises from a second-order coupling process that requires breaking the screw symmetry of the diamond lattice. Numerically accurate tight-binding simulations suggest that valley splittings needed for qubit operation can be achieved using realistic shear strains (εxy ≈ 0.1%), while the required Ge concentration oscillations (λ = 1.7 nm) have already been demonstrated in the laboratory25. While “intrinsic” strain sources such as metallic gates, dislocations, and dielectric layers do not provide a sufficiently large shear strain for our purposes50,51,52,53,54, our strain simulations confirm that several different etching techniques could be used to achieve such strain. Overall, the fabrication requirements for STRAWW are much less challenging than other schemes, including ultra-sharp interfaces and short-period Wiggle Wells, making this a very attractive approach for managing valley splitting in future qubit experiments. Moreover, spin-orbit coupling is also enhanced in long-period Wiggle Wells, which may be exploited for qubit manipulation27. We expect that future devices could provide shear strains larger than those reported here, through a variety of implementation strategies.

Methods

sp3d5s* tight-binding model

We use an sp3d5s* tight-binding model30 to study valley coupling in Si/SiGe quantum wells. This is an atomistic model with nearest-neighbor hopping terms, including ten spatial orbitals at each atom site. Such models are well established for accurately modeling the electronic structure of many different semiconductors31. Spin-orbit coupling is typically introduced into these tight-binding models through an intra-atomic coupling between p orbitals55. However, this has no quantitative effect on the valley splitting results studied here, and is therefore disabled in the current analysis, for simplicity. On the other hand, we incorporate distinct Si-Si, Ge-Ge, and Si-Ge nearest-neighbor hopping terms, following ref. 30, to more accurately represent SiGe alloys.

Strain is incorporated into the model through the equation

$${{{{\boldsymbol{R}}}}}_{i}=\left(1+{{{\boldsymbol{\varepsilon }}}}\right){{{{\boldsymbol{R}}}}}_{i,0}\pm \zeta \frac{{a}_{0}}{4}\left({\varepsilon }_{yz},{\varepsilon }_{xz},{\varepsilon }_{xy}\right),$$
(7)

which relates the location of atom i in the presence of strain (Ri) to its unperturbed location (Ri,0). Here, ε is the strain tensor, the signs + and − are assigned depending on whether atom i belongs to the red or blue sublattice, respectively (see Fig. 1a), and ζ is Kleinman’s internal strain parameter56, which is used in diamond crystal lattices to account for the relative shift of the two sublattices within a unit cell due to shear strain. We ignore the small difference between ζ values for Si vs Ge atoms, simply adopting ζ = 0.53 throughout the structure57. Strain is then incorporated into the tight-binding Hamiltonian in two ways: (i) strain-dependent onsite couplings, following ref. 30, and (ii) modified bond lengths and angles, which result in modified hopping terms58,59. Further details on our implementation of the sp3d5s* tight-binding model are provided in ref. 27.

We consider a sigmoidal-interface model13,15 with sinusoidal oscillations for the Ge concentration profile in the tight-binding calculations, given by

$${n}_{{{{\rm{Ge}}}}}(z)=\frac{{n}_{{{{\rm{bar}}}}}}{1+{e}^{4z/w}}+2{\bar{n}}_{{{{\rm{Ge}}}}}{\sin }^{2}\left(\frac{\pi z}{\lambda }\right),$$
(8)

where nbar = 0.3 is the Ge concentration in the barrier region, w is the interface width, \({\bar{n}}_{{{{\rm{Ge}}}}}\) is the average Ge concentration in the quantum well (associated with the Ge concentration oscillations), and λ is the oscillation wavelength. Note that the Ge concentration oscillations in Eq. (8) extend across the heterostructure (including the barrier region). In realistic devices, the Ge oscillations would likely only occur in the quantum well region, as illustrated in Fig. 1k. However, restricting the oscillations to the well region in the simulations produces kinks in nGe profile, which are known to artificially boost the valley by enlarging the short-wavelength Fourier components of nGe13. Such kinks are not expected to be present in realistic devices. Note that we have numerically verified that restricting the Ge concentration oscillations to the quantum well region does not significantly alter the valley coupling arising from the combination of Ge concentration oscillations and shear strain. We therefore avoid any such effects here by extending the Ge concentration oscillations across the whole structure. We also note that the bottom quantum well interface has been excluded in Eq. (8), because the electric field used in our simulations is always large enough to push the electron wave function tightly against the top interface. For narrower quantum wells, where this would not be the case, we do not expect the valley splitting provided by STRAWW to be significantly affected by including a bottom interface. This is because the valley coupling within STRAWW does not fundamentally rely upon interface effects, in contrast to “conventional” Si/SiGe quantum wells without Ge concentration oscillations.

Envelope-function method

Here, we use an envelope-function approach to derive Eq. (5) of the main text within the effective-mass framework of Eq. (1). To begin, we note that the energy scale of the intra-valley Hamiltonian H0 dominates over the inter-valley Hamiltonian Hv. We can therefore calculate EVS by first solving for the ground state of H0, and then computing the matrix element of Hv within first-order perturbation theory.

We can solve H0 straightforwardly with an effective-mass approximation. First, we note that the ground state ψ of H0 (or any other eigenstate) may be expanded as33

$$\psi (z)=\mathop{\sum}\limits_{n}{F}_{n}(z){U}_{n}(z),$$
(9)

where {Un} comprises a complete and orthogonal set of Bloch functions that satisfy the k = 0 Bloch-Schrödinger equation,

$$\left[-\frac{{\hslash }^{2}}{2{m}_{l}}{\partial }_{z}^{2}+{V}_{0}\cos \left(\frac{2\pi z}{\lambda }\right)\right]{U}_{n}(z)={E}_{n}{U}_{n}(z),$$
(10)

and Fn are envelope functions that account for the effects of the confinement, Vqw. Note that the Bloch functions here do not have the periodic structure of the crystal lattice, but rather the periodic structure of the WW, which enters H0 through the potential V(z) in Eq. (3). Un are therefore periodic over the length scale λ, while Fn are slowly varying over this length scale. Here we adopt the conventional normalizations \({\lambda }^{-1}\int\nolimits_{0}^{\lambda }| {U}_{n}(z){| }^{2}dz=1\) and ∑n∫ ∣Fn(z)∣2dz = 1. Plugging Eq. (9) into the Schrödinger equation yields the coupled envelope equations

$$\begin{array}{ll}-\frac{{\hslash }^{2}}{2{m}_{l}}{\partial }_{z}^{2}{F}_{n}-\mathop{\sum}\nolimits_{m}\frac{i\hslash }{{m}_{l}}{p}_{nm}{\partial }_{z}{F}_{m}(z)\\+\,\mathop{\sum}\nolimits_{m}\int\,{V}_{nm}(z,{z}^{{\prime} }){F}_{m}({z}^{{\prime} })\,d{z}^{{\prime} }=(E-{E}_{n}){F}_{n}(z),\end{array}$$
(11)

where

$${p}_{nm}=\frac{-i\hslash }{\lambda }\int\nolimits_{0}^{\lambda }{U}_{n}^{* }{\partial }_{z}{U}_{m}\,dz,$$
(12)

and pnn = 0, and \({V}_{nm}(z,{z}^{{\prime} })\) is a non-local potential arising from Vqw, whose form is given in ref. 33.

Up to this point, the expansion of Eq. (9) and the following equations are exact. However, the Schrödinger-like, coupled envelope equations, Eq. (11), can be effectively decoupled via a canonical transformation, yielding the much simpler result, ψ(z) ≈ F0(z)U0(z), where F0(z) satisfies an effective mass equation. To derive this result, we note that the non-local and inter-band nature of the potential \({V}_{nm}(z,{z}^{{\prime} })\) arises from the Fourier components of Vqw in the outer-half of the Brillouin zone, i.e., for large wavevectors ∣k∣ > π/(2λ). Assuming that Vqw varies slowly compared to λ, these Fourier components are insignificant, and we can ignore all non-local and inter-band components in \({V}_{nm}(z,{z}^{{\prime} })\). In other words, there is a separation of length scales leading to the following local approximation33 for Eq. (11):

$$\begin{array}{ll}-\frac{{\hslash }^{2}}{2{m}_{l}}{\partial }_{z}^{2}{F}_{n}\,-\,\frac{i\hslash }{{m}_{l}}\mathop{\sum}\limits_{m}{p}_{nm}{\partial }_{z}{F}_{m}\\\,+\,{V}_{{{{\rm{qw}}}}}(z){F}_{n}(z)=(E-{E}_{n}){F}_{n}(z).\end{array}$$
(13)

Now, there is also a large separation of energy scales that we can use to simplify the envelope equations. The largest energy scale in Eq. (13), by far, is the splitting between the different Bloch modes, En − E0 ~ Eλ = 2ℏ2π2/(mlλ2)(n ≥ 1). In the absence of coupling between these Bloch modes (i.e., for pnm = 0), the confinement energy scale arising from Vqw is of order of 2ℏ2π2/(mll2) ≪ Eλ, where l is the width of the quantum well, while the inter-mode coupling term, which scales as 1/(lλ) is intermediate between these two energy scales. A perturbative treatemenmt of the coupling is therefore justified. Applying a Schrieffer-Wolff transformation, we obtain the desired single-mode solution ψ(z) ≈ F0(z)U0(z), where F0 satisfies the effective-mass equation,

$$-\frac{{\hslash }^{2}}{2{m}_{l}^{* }}{\partial }_{z}^{2}{F}_{0}+{V}_{{{{\rm{qw}}}}}(z){F}_{0}(z)\,\approx\, (E-{E}_{0}){F}_{0}(z),$$
(14)

and the renormalized effective mass is given by

$$\frac{1}{{m}_{l}^{* }}=\frac{1}{{m}_{l}}-2\frac{1}{{m}_{l}^{2}}\mathop{\sum}\limits_{n\ge 1}\frac{{\left\vert {p}_{n0}\right\vert }^{2}}{{E}_{n}-{E}_{0}}.$$
(15)

Equation (14) is a standard effective-mass equation, where the periodic potential associated with the WW has been absorbed into the renormalized effective mass. However, the effective-mass correction (\({{{\mathcal{O}}}}[{V}_{0}^{2}]\)) is very small for typical heterostructures, since V0 ≲ 20 meV, while Eλ ≈ 565 meV for λ = 1.7 nm, such that \(({m}_{l}^{* }-{m}_{l})/{m}_{l}\,\lesssim\, 1{0}^{-3}\). It is therefore a very good approximation to ignore the effective-mass renormalization. The leading-order correction in this formalism (\({{{\mathcal{O}}}}[{V}_{0}]\)) appears only in the Bloch function U0, which to leading-order in V0 is given by

$${U}_{0}\,\approx\, 1+({V}_{0}/{E}_{\lambda })\cos (2\pi z/\lambda ).$$
(16)

Finally, we are in a position to compute the inter-valley matrix element Δ = 〈ψ∣Hv∣ψ〉 using ψ(z) = F0(z)U0(z). The result contains many terms, but is greatly simplified by ignoring the higher-order \({{{\mathcal{O}}}}[{V}_{0}^{2}]\) terms, terms involving derivatives of F0, and integrals containing highly oscillatory plane waves that average toward zero. [Note that terms involving derivatives of the envelope function F0 are insignificant, because the Fn are slowly varying compared to the fast-oscillating U0 terms.] A straightforward calculation then leads to Eq. (5) in the main text, and the corresponding valley splitting is given by \({E}_{{{{\rm{VS}}}}}=2\left\vert \Delta \right\vert\).

Strain calculations

Shear strain calculations were performed using the Solid Mechanics module in COMSOL Multiphysics39. Below, we describe the materials properties assumed in these simulations, including the coefficients of thermal expansion (CTE), which describe thermal contractions when the device is cooled from room temperature (293.15 K) to 1 K.

For the top-trench geometry of Fig. 4a, we assume a quantum well formed of a 9 nm strained-silicon layer sandwiched between a thick strain-relaxed buffer layer and a 50 nm top layer of strain-relaxed Si0.7Ge0.3. In a typical device, we would assume a buffer layer thickness of order 500 μm, which is challenging to simulate. In our simulations, we approximately account for such thick layers by assuming a thinner layer of width 2 μm (which is still much thicker than the top layers), and adopting a zero-displacement boundary condition, as defined in ref. 39. The total volume of the resulting simulation is about 3.2 × 103 μm3. Biaxial strain is applied to the Si layer through the initial-strain parameters εxx = εyy = 1.24%, and εzz = − 1.01%.

The CTEs of Si and SiGe depend weakly on temperature, while COMSOL assumes constant CTE values. To account for this in our simulations, we simply adjust the CTE values in the COMSOL parameter library. Averaging over the CTEs provided in refs. 60,61,62 and applying Vegard’s law to describe the SiGe alloy, we find the temperature-adjusted coefficients to be αSi = 0.76 × 10−6 K−1 for Si, and \({\alpha }_{{{{{\rm{Si}}}}}_{0.7}{{{\rm{Ge}}}}_{0.3}}=1.52\times 1{0}^{-6}\,{{{\mbox{K}}}}^{-1}\) for the SiGe. For both Young’s modulus E and the Poisson ratio ν, thermal corrections amount to only a few percent at most; we therefore use room temperature values for these parameters, as given in the COMSOL parameter library. To fully account for the 500 μm Si buffer layer (which is not included in the simulation), we also include the thermally corrected Si CTE, αSi, to describe the contraction of the bottom surface of the simulated device. To check the validity of our approximate treatment of the thick buffer layer, we also simulate thicker systems, to check for convergence, and we relax the boundary conditions by applying COMSOL’s rigid-motion-suppression feature.

For the free-standing membrane geometry shown in Fig. 4d, we adopt the heterostructure parameters shown in Fig. 4e. We also assume a trench height of h = 500 μm. Here, we simulate a much larger total volume of about 5 × 106 μm3, to more accurately describe the effects of the deep trench. Biaxial strain is imposed as described above, and we account for depositional strain in the Si3N4 stressor by imposing an intrinsic tensile stress of 1 GPa43. Here again we relax the boundary conditions using COMSOL’s rigid-motion-suppression feature. To account for thermal contraction, we take the same approach as above, with the additional temperature-adjusted CTEs given by \({\alpha }_{{{{{\rm{Si}}}}}_{3}{{{\rm{N}}}}_{4}}=0.5\times 1{0}^{-6}{{{\mbox{K}}}}^{-1}\) and \({\alpha }_{{{{\rm{Si}}}}{{{\rm{O}}}}_{2}}=-0.2\times 1{0}^{-6}{{{\mbox{K}}}}^{-1}\)63,64,65. We note that nearly identical shear-strain results can be obtained using room-temperature CTE values from the COMSOL library without accounting for cryogenic cooling, indicating that depositional strain from the Si3N4 stressor dominates over thermal contraction in this geometry.