Abstract
Coupled Thermal-Hydraulic-Mechanical-Chemical (THMC) approaches may be important for assessing the long-term durability of cementitious materials. We present a multiphysics approach to overcome past limitations of THMC modelling and validate it based on experimental results of accelerated carbonation tests. Our numerical approach rests on a sequential coupling between Hytec and Cast3m. Hytec computes the evolution of hydraulic and mineralogical fields allowing to compute the micromechanical properties (e.g. Young’s modulus). The mineral reactions generate tensile stresses and Cast3M computes the associated strain tensors and the damage evolution represented by the opening or sealing of cracks, impacting subsequent reactive transport processes. Our approach manages to qualitatively represent the crack patterns and non-uniform degradation depths observed on microtomographic images of carbonated cement samples, which can only be explained by the coupled dynamics of chemical and mechanical processes. Our approach can be extended to a wide range of cement-concrete pathologies and contexts.
Similar content being viewed by others
Introduction
In recent years, the need for accurate and powerful computational methods has increased for many fields of earth and material science. They constitute powerful tools for decision-making and to understand complex coupled systems. For example, reactive transport modelling has emerged at the end of the 20th century mostly in the context of contaminant transport for groundwater quality1. Now, this field has grown to tackle more and more applications2, including the description of material degradation, for example in radioactive waste repositories3,4. The impact of geochemical reactions within a porous medium can significantly alter its properties5,6, further impacting its response to various perturbations. However, the mechanical response of the material which has undergone microstructural changes5,7,8 has almost always been neglected, as were the chemical effects for geomechanical calculations. This is primarily due to the fact that a coupled description of these phenomena significantly increases the complexity of the model formulation.
The degradation of porous reactive materials is a prime example in which mechanical and chemical evolutions are coupled and exert a feedback on each other, often through the appearance or sealing of cracks. As examples, we can cite the chemical induction of fractures within lithium batteries9, the durability of geomaterials in the reservoir context10,11, or concrete8,12,13, melting of nuclear pellets14 or the corrosion and hydrogen transport in steel15. On a larger scale, we can cite the durability of injection wells for gas reservoirs16 or concrete dams17,18, the induced seismicity associated with various applications19,20,21,22.
In past attempts to model thermo-hydraulic-mechanical-chemical (THMC) effects, several key issues have rarely been addressed. In particular, the dynamic two-way coupling between chemistry and mechanics is generally not described. For example, mineralogical evolutions obtained from reactive transport (RT) simulations were used to evaluate the potential evolution of strains and stresses. This allowed some authors to evaluate whether or not a mechanical failure could occur23,24,25,26. The appearance, propagation of cracks and its impact on the subsequent reactive transport processes have rarely been included in such coupled approaches10,12,27,28,29,30. Also, RT simulations often neglect one or several processes which may have a significant effect on the mechanical response, such as the porosity evolution or the water balance (consumption, evaporation)13,31,32,33.
In this research paper, we propose a generic fully dynamically-coupled THMC approach to predict the appearance and propagation of cracks in deformable porous materials. This approach is suited to describe the generic reactive transport processes (i.e. mineral dissolution and precipitation, drying, porosity evolution, gas transport, heat transfer) and the mechanical damage they exert (i.e. shrinkage, swelling, cracking) under various thermo-hydro-chemo-mechanical loadings. This approach is based on the numerical coupling of Hytec, a reactive transport simulator34 and Cast3m, a mechanical Finite Element (FE) code35 as depicted in Fig. 1.
We focus our developments on the specific case of the accelerated atmospheric carbonation of cementitious materials, which is a ubiquitous process responsible for important CO2 uptake36. Both Hytec37 and Cast3m have been used38,39 to describe this cement pathology. When a cementitious material is in contact with the atmosphere, CO2(g) diffuses through the pores, dissolves in the pore-water and reacts with dissolved calcium to precipitate CaCO3. This reaction is known as carbonation and has been extensively studied for decades as it leads to a significant changes in mineralogy (coupled decalcification and precipitation of CaCO3)40,41, microstructure and transport properties42,43,44,45,46,47. The densification linked to the fixation of exogenous CO2 leads to an increase in the mechanical properties of the material (elastic modulus, strength)48,49,50,51,52 but makes it more brittle53,54,55. In practice, carbonation is one of the most detrimental degradation phenomenon for concrete durability as it induces uniform corrosion of the reinforcing steel bars56,57,58. This degradation involves the coupling of several processes: gaseous migration and dissolution; mineral dissolution and precipitation as well as porosity evolution59; release, evaporation and transport of water60; solid phase shrinkage61,62,63 and tensile stresses leading to the appearance of cracks64,65,66. Seigneur et al.60 have shown that reactive transport modelling alone was not able to reproduce the observed degradation depths and the reaction fronts as soon as a crack pattern was observable. The development of microcracks is attributed to shrinkage induced by both carbonation reactions and drying processes. These mechanisms have not yet been addressed with a fully coupled THMC formulation including either the appearance and propagation of cracks or their effects on transport properties. Therefore, we use our approach to overcome the previous limitations and tackle the THMC problem of unsaturated carbonation in cementitious materials.
The goal of this application is to study whether or not our approach is suited to the description of such THMC processes. A thorough quantitative validation of simulation results would require accurate 3D data acquisition (e.g. crack distribution) which are intrinscally challenging to extract from microtomographic images. Furthermore, the main objective of our approach is its upscaling and generalization: it is not meant to perform a pore-scale thorough description of these processes. We mostly focus on describing the macroscopic behaviour of engineering materials with an emphasis on degradation depths and patterns as well as the crack distribution within the studied sample and it consequences on the chemical degradation.
Results
Sample characterization and core degradation
In this study, we focus on a cylindrical cement paste sample (radius R = 15 mm, height H = 110 mm) obtained by the hydration of C3S described in Kangni-Foli et al.66. The mineralogy of this hydrated C3S paste only consists in Portlandite (calcium hydroxyde) and an amorphous calcium-silicate-hydrate (C-S-H) phase. C-S-H corresponds to the binding phase67 of cementitious materials. It is structurally built as a layered structure with polymerized silicate chains whose nanostructure is comparable to tobermorites68,69,70. Following the calcium over silica atomic ratio (Ca/Si), different degree of polymerization of silicate chains are observed71,72,73. When subject to leaching or carbonation, the Ca/Si ratio of the hydrates progressively decreases which leads to a microstructural modification of the C-S-H phase, associated with a reduction in molar volume and thus shrinkage66,74,75,76. In our sample, the initial calcium over silica atomic ratio (Ca/Si) of the C-S-H is 1.6. The sample initial total porosity is 40%, determined from oven drying at 105 ∘C, with a 25% volume fraction of portlandite (obtained from thermogravimetric analyses). More details on the miscrostructure and experimental characterizations can be found in Kangni-Foli et al.66.
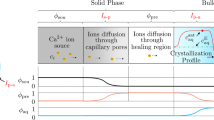
Microtomographic images of the carbonated samples were obtained and revealed three distinct density-zones (Fig. 2a,c and Supplementary Video): a completely carbonated zone (close to the exposed surface in light-grey on Fig. 2c and Supplementary Video); a transition zone (dark-grey) that was partially carbonated and then the non-carbonated zone (light green). It is noteworthy that the carbonation depth was not uniform and that the partially carbonated zone showed an unexpected bell-like frontier. These features were however supported using phenolphtalein (Fig. 2b) that showed similar pH distribution (note that phenolphtalein is a pH indicator that turns pink at high pH corresponding to sound material, and that is used to probe the extent of carbonation). Figure 2a and the Supplementary Video show the crack distribution within the sample induced by carbonation shrinkage. These cracks modified the carbonation front and induced the bell-like frontier as well as a locally deeper carbonation front. Noted that the 2D microtomographic image in Fig. 2a only highlight the larger crack resulting from the sample deformation, but it does not show the microcrack network which is below microtomographic resolution.
a 2D section of a microtomographic image showing a non-uniform carbonation front. Largest visible cracks are highlighted in red and are associated to local increased degradation depths. b 2D observation of a phenolphtalein test revealing the carbonation fronts (after 81 days of carbonation). The spatial scale is given in cm. c 3D microtomographic image of the sample. The green zone depicts the sound hydrated C3S paste, the dark-grey corresponds to the transition zone, while the fully carbonated paste is represented in light grey (top part). These elements can be observed dynamically in the Supplementary Video.
Model formulation
Reactive flow processes include the migration of water, transport of solutes and gaseous species within a porous medium while accounting for the solid-liquid-gas equilibrium. We use the fully coupled reactive transport approach of Hytec34,37,77. Release and consumption of water by chemical reactions are included and coupled with the unsaturated flow, as well as water evaporation, controlled by the sorption isotherm43, described by the Van Genuchten empirical relation78. To represent the appearance and local effect of cracks, a double porosity approach has been used79,80,81,82. It represents that each gridcell is a combination of two interconnected domains, the matrix (superscript m) with a porosity ωm and the cracks (superscript c) with a porosity ωc. Transport and reactions can occur independently within each domain but they influence each other through cross-domain fluxes. The crack properties (diffusion Dc, permeability Kc) are evaluated based on their apertures.
Hytec models the evolution of the mineralogy, allowing to evaluate both the evolution of the poro-elastic properties of the material and the carbonation shrinkage Equation (2). The poro-elastic properties are computed through the use of the Mori-Tanaka scheme5,8,83,84,85. For this, the cement system is represented as an evolving matrix phase (the C-S-H phase with its gel porosity) with several spherical inclusions representing portlandite, capillary porosity and calcite.
Then, the poromechanical model includes material deformation and damage induced by the evolution of porosity, mineralogical and pore-pressure fields. The damage model is supposed to be isotropic and the crack density is modelled through a classical damage scalar variable d86, varying between 0 for sound material and 1 for totally degraded one. We assume that the material behaviour can be described by the behaviour law:
where \(\underline{\underline{\sigma }},{\mathbb{C}},\underline{\underline{\varepsilon }}\) and \(\underline{\underline{I}}\) are the Cauchy stress, stiffness, total strain and identity tensors, respectively. The last term represents the macro-stress induced by pore pressure where bm is the Biot coefficient estimated from the elastic properties and ΔPm = Δ(SlPl) + Δ((1 − Sl)Pg) represents the pore pressure variation from the initial state which plays a significant role on the degradation process18,87,88 and for drying shrinkage89. Sf and Pf respectively represent the saturation and pressure in fluid phase f (liquid–gas). The impact of water production/evaporation can significantly modify these values90, which is considered in Hytec thanks to its full description of water as a reacting species77. The pressure exerted in the crack domain is neglected due to the fact that the cracks are mostly desaturated. \({\underline{\underline{\varepsilon }}}^{\xi }\) models the homogenized internal free strain related to chemical reactions. Based on66,74, carbonation shrinkage is assumed to evolve with the variation of the volume fraction of the equivalent C-S-H phase \(\Delta {\varphi }_{{{{\rm{CSH}}}}}^{{{{\rm{eq}}}}}\) during its decalcification. This volume fraction includes the different Ca/Si ratio as well as the C-S-H intrinsic gel porosity, whose initial value is estimated at 9%. This yields a C-S-H phase initial volume fraction of 44%. For more details about the computation of theses volume fractions from Hytec simulation, see “Governing equations”. The homogenized carbonation shrinkage strain \({\underline{\underline{\varepsilon }}}^{\xi }\) can then be computed using a shrinkage coefficient αξ describing the macroscopic effect of the C-S-H phase shrinkage occurring locally in the form:
The damage estimation is based on the Fichant-Laborderie model91,92 (see Table 1). The crack opening displacement vector \(\left[{{{\bf{u}}}}\right]\) is calculated from the anelastic tensor91, which has been applied and validated in several studies involving concrete18,93,94 (see “Governing equations”). The damage scalar variable and the normal crack aperture are used to estimate the evolving crack porosity ωc and their transport properties, respectively, which are updated in the reactive transport model.
The study focuses on the simulation of the isothermal accelerated carbonation of a hydrated C3S paste. Simulations are parametrized with the Thermodem thermodynamic database95, and dedicated measurements on the C3S sample including mineralogy, porosity, initial gas diffusion coefficient, Van Genuchten parameters and water content. More details about the hydrogeochemical description of our materials are given in60.
Based on the initial microstructure and phase assemblage, the poroelastic properties estimated using the Mori-Tanaka scheme yields an initial Young Modulus of 14.47 GPa, in agreement with the measured value 15 ± 1 from Kangni-Foli et al.66 (see “Governing equations”). The other initial poroelastic properties are given in Table 1. The progressive decalcification of the C-S-H phase is modelled using a discretized set of dissolution-precipitation reactions towards hydrates with lower Ca/Si atomic ratios60, ranging from 1.6–1.2–0.8 and amorphous silica.
The simulation of the cylindrical sample by a chemical unilateral loading is modelled through a 2D axisymmetric simulation with a 30 mm diameter and a length of 110 mm (Fig. 3). For the RT simulation, atmospheric cells are used to model gaseous exchange (CO2 and water vapor)60, while the other boundaries do not allow any mass transfer. No external mechanical loading is applied on the sample, but internal stresses are induced by carbonation shrinkage and the variation of pore-pressure associated with the release of water and porosity changes.
Mesh and boundary conditions of the reactive flow and mechanical systems. We model a 2D-axisymmetric domain whose dimensions correspond to the experimental samples (R = 15 mm, Height = 110 mm). A rectangular grid was used with cell dimensions of Δr = 0.75 mm along the radius and Δz = 2 mm along the cylinder axis.
Thus, this approach constitutes a physical two-way dynamic description of the coupled THMC processes. Its numerical implementation is detailed below (Fig. 6). In addition, the use of the fully-coupled nature of Hytec, allows our approach to overcome the previous past limitations.
Simulation results
Results of our THMC simulation are presented with 2D profiles along the sample diameter. For visualization purposes, profiles focus on the first 35 mm of the sample near the atmospheric boundary.
Figure 4 shows the evolution of chemical and mineralogical maps after 40, 160 and 326 days of accelerated carbonation. As carbonation proceeds, portlandite (Fig. 4a) and C-S-H (Fig. 4b) are progressively dissolved and replaced by calcite (Fig. 4c) and amorphous silica (Fig. 4d). A more detailed analysis of the amorphous silica precipitation and C-S-H decalcification obtained with our reactive transport model is provided in our previous work60. These reactions result in a decrease of the pore-water pH (Fig. 4f) and porosity from 0.4 to 0.3 (Fig. 4e) in accordance with experimental results, where the porosity measured in the carbonated area is around 0.28 ± 0.0566. Furthermore, the solid mass density estimated in the carbonated zone (not shown) is equal to 2.06 g.cm−3, which is comparable to the experimental measurement of 2.11 g.cm−3 66.
Displayed maps focus on the first 35 mm close to the atmospheric carbonation, and show mineralogical, geochemical and hydraulic profiles along the sample diameter. a Portlandite volume fraction. b C-S-H volume fraction with a Ca/Si of 1.6. c Calcite volume fraction. d Amorphous silica volume fraction. e Matrix porosity evolution. f pore-water pH (initial value: 12.5). g Liquid saturation. h Effective gaseous diffusion coefficient.
The modelled carbonation depth, associated with Portlandite dissolution, is also consistent with observation. At the early stages of carbonation (40 days), most mineralogical fronts are uniform, in accordance with results obtained without accounting for the mechanical response of the material60. However, a crucial improvement of our THMC approach is that it captures the non-uniform development of the carbonation front with a deeper carbonation near the sample edges. The pH map as well as the other reaction fronts can be compared to the phenolphtalein test shown in Fig. 2b. Furthermore, the model simulated correctly the three area described in the Fig. 2c and supplementary video, comprising a completely carbonated zone (only calcite and amorphous silica), a transition zone (partly dissolved portlandite, calcite and C-S-H 1.6) and then the non-carbonated zone (initial mineralogy).
In addition to porosity reduction, mineral reactions exert several feedbacks on the carbonation progress which are highlighted in Fig. 4. First of all, the important release of water associated with the dissolution of C-S-H and portlandite induces a significant saturation front (Fig. 4g) yielding an increase in fluid pressure, relative permeability and a decrease in gas transport (Fig. 4h). These effects act together against an in-depth carbonation and should therefore homogenize the carbonation front along the sample diameter as radial diffusion may be favoured over axial migration. However, as carbonation proceeds, the extent of the carbonation front increases, predominantly along the edges, due to localized mechanical damage, as shown in Fig. 5.
As sound C-S-H (with a Ca/Si ratio of 1.6) evolves towards amorphous silica, significant shrinkage occurs (Fig. 5c) in parallel to an important release of water, inducing tensile stresses and increasing pore-pressure within the material (Equation (1)). These local strain induces the sample deformation that mainly occur at the edges of the sample, resulting in localized damage (Fig. 5b) and larger microcracks along the edges (Fig. 5a). These constitute preferential diffusive pathways for CO2 within the material, accelerating the degradation predominantly near the edges of the sample. This leads to a non-uniform carbonation front and carbonation shrinkage. It must be acknowledged that the carbonation fronts are relatively smooth compared to what is usually expected. This is due to the fact that we allowed the simulation to use a rather high timestep. This results in a deeper CO2 ingress, slightly diluting the portlandite dissolution front. However, carbonation shrinkage is function of the equivalent C-S-H volume fraction (2), and is maximum at the transition towards amorphous silica, whose front remains sharp (Fig. 4d). Thus, the impact of this timestep on the relevant coupled chemo-mechanical processes is minimal. Furthermore, it is important to note that cracking, which is the main mechanical impact on the reactive transport, is mesh independent due to our use of Hillerborg regularization techniques (see “Governing equations”).
These results highlight the ability of the model to tackle chemo-mechanical coupling effect28, where damage increases the material diffusivity and permeability and induces preferential diffusion paths, triggering in turn a localization and an acceleration of the chemical degradation as reported in96 and97.
Another important aspect of our approach is that it allows to estimate the evolution of the mechanical properties (Young’s modulus, Biot coefficient and αξ) of the cement paste sample, whose evolutions are also displayed in Fig. 5c–e. The Young’s modulus increases in the carbonation front zone due to a progressive replacement of portlandite by calcite, which results in a porosity decrease while leaving the C-S-H phase intact. Then, upon carbonation, as portlandite locally disappears, the C-S-H is in turn subject to decalcification which decreases its stiffness, as expressed by Equation (11). The Young’s modulus admits its maximum value near the carbonation front, with the presence of both portlandite and calcite. Interestingly, the porosity does not exhibit its minimum value in the corresponding zone (see Fig. 4). In that way, there is not a direct link between the stiffness and the porosity of the cement paste. The heterogeneity of the carbonation front induces a heterogeneity of the material properties that impacts the global mechanical response. Then, the damage variation is influenced by the local chemical strain and macroscopic sample deformation, as described in8,13. Finally, due to the complex mechanical behaviour and the method used to estimate the crack opening, no direct and simple relationship between the normal crack opening and the damage fields can be identified. This highlights the necessity to estimate the crack opening to model the crack transport properties97.
Discussion
The good qualitative representation of the carbonation fronts, the generated crack patterns and the correct evolution of various properties (porosity, density) is a validation of our approach to the THMC processes involved in the carbonation of a hydrated C3S paste. While not immediately transposable, our process-based approach has the potential to accurately represent the carbonation and/or other pathologies to various cement formulations, e.g. high-Al content with C-A-S-H phases98. Such verification constitutes the important following step of our study. Then, the following developments in the context of cementitious material durability will focus on studying various chemo-mechanical loadings and boundary conditions as well as including coupled transient thermal and hydraulic gradients. For example, chemical degradation of concrete from sensitive civil engineering facilities (e.g. nuclear reactor containment building, dam) can be tackled by including the transient drying mechanisms, which may themselves trigger delayed strain induced by chemical reactions. In the case of carbonation, the competing effect of chemical strains and drying will be more deeply analyzed to better capture the respective importance of these phenomena on microcracking development. Our approach could be extended to account for swelling reactions, which constitute another chemo-mechanical pathology of concrete of major relevance for the industry99. Further, the complex coupled THMC nature of hydration processes, which have an essential impact on the durability of concrete structures, could also be described by this approach. Note that the aforementioned chemical degradations necessitate in general the development of specific chemical strain models, depending in particular on the overall mineralogy evolution.
Further, a more representative mechanical behaviour of the material will be obtained by accounting for long-term creep phenomena. This would be of particular importance when our method will be used for more complex materials. For example, in concrete, viscous phenomena induce a redistribution of stresses and strains at the mesoscale (e.g. between aggregates and cement paste) with important structural consequences. Thus, a mesoscale concrete description should explicitly model aggregates and interfaces and include the creep phenomea30,97,100. Last, the description of microcracking and fracturing remains a challenging topic especially in coupled physical phenomena not necessarily occurring at the same characteristic scale. In this regard, alternative approaches could be tested to better reproduce some key features of crack modelling; for instance, an orthotropic description of discrete crack planes is likely to improve the whole model results, compared to the current more diffuse representation related to the damage continuous approach and the isotropic diffusion and permeability tensor.
Our approach allows to dynamically model processes whose coupled description has been a challenge for decades. Considering its physical and phenomenological roots, this approach can be generalized and extended. It opens perspectives for THMC modelling in various contexts, including corrosion and cracking induced by the precipitation of expanding phases (sulfate attack or alkali-silica reactions). Given the multiphase capacities of the reactive transport simulator, it can be used in the context of gas repositories to predict the durability of injection wells. Also, it can be of particular interest for hydrogen reactivity, either in the context of hydrogen storage101 or during the transient hydraulic phase of nuclear waste repositories102,103. On a larger scale, coupled chemo-mechanical reactions are linked to induced seismicity104 which could constitute another exciting perspective of this work.
Methods
Experimental conditions
Post-hydration and prior to carbonation, C3S samples were equilibrated in a climatic chamber with \(25^\circ{\rm{C}}\) and 55% relative humidity (RH) to maximize the effect of carbonation105,106. Accelerated carbonation was then triggered by setting a CO2 partial pressure of 0.03 bar, which was found to be representative of natural carbonation76. The lateral and bottom surfaces of the samples were covered with adhesive aluminium foils to obtain a one-dimensional degradation along the axis. Several carbonated samples were collected after 30, 80 and 326 days to characterize the carbonation depth and the crack patterns.
X-ray computed microtomography (XCT) was used to observe the microstructural changes induced by carbonation. XCT is a non-destructive technique that is sensitive to differences in density (linked in our case to CO2 incorporation). The scans were carried out using a General Electric (GE) V∣tome∣x M device (see66 for details about the operating conditions). The image reconstruction was done using GE proprietary software resulting in volumes that were post-processed using VG Studio Max (Volume Graphics) with a voxel size of 29.7 μm.
Governing equations
Parameter definition and values are listed in Table 1.
Reactive transport
Richards equation is solved to compute water migration through the porous medium:
where μl is the liquid viscosity and \({P}_{\nu }^{{{{\rm{l}}}}}\) is the liquid pressure within continuum ν. The unsaturated properties of the porous medium (relative permeability krl(Sl), sorption isotherm Pl(Sl)) are described using Van Genuchten relations78. Qν is the chemical source term of water in domain ν and \({J}_{{{{\rm{dual}}}}}^{\nu }\) is the water flux towards domain ν:
where \({{{\mathcal{A}}}}\) represents the total surface area of the crack domain (m2.m−3), \({{{\mathcal{D}}}}\) is a characteristic length (m), and the superscript c, m represents the harmonic average between the properties of the two media. Solutes and gasesous species migrate by advection (following Darcy velocity ul) and diffusion in the fluid phases following the traditional reactive transport equations77.
where \({T}_{i,\alpha }^{\nu }\) is the total concentration of species i within fluid phase α in continuum ν (mol.L−1 of phase α). \({R}_{i}^{\nu }\) is the chemical source term for species i in domain ν. The solid-liquid-gas equilibrium is solved with a thermodynamic database under the assumption of a thermodynamic equilibrium between the three phases. \({\phi }_{\alpha }^{\nu }\) is the cross-domain diffusive flux of species i towards ν
where28
Equation (7) is based on the experimental work of Djerbi et al.107 and it is assumed that the diffusion coefficient evolves linearly with the crack opening until a critical value uref. This kind of model has been used in several works57,97,108. The effective diffusion coefficient for phase α is described by a Millington-Quirk relation109:
with \({D}_{\alpha }^{{{{\rm{ref}}}}}\) represents the free-phase diffusion coefficient (m2.s−1).
Poromechanics
There exists several mechanical approaches to describe the appearance and propagation of deformation-induced cracks. Cracks can be explicitly described through fracture mechanics models such as XFEM110 or frictional cohesive zone models13, or can be included through a continuum approach such as damage mechanics8. However, with the perspectives of upscaling our approach to large structures or geological settings, continuum models accurately describing the evolution of macro-scale properties and structural damage are required. For these reasons, we have chosen a continuous porous medium approach where the mechanical fracture is simulated using a damage model, which has already yielded satisfactory results for leaching12 and corrosion39.
Using a damage behaviour requires a dedicated regularization method in order to avoid a mesh dependency. The damage is modelled through Fichant-Laborderie model91,92,111 and its regularization is performed using Hillerborg’s energetic method91,112. The associated equations are depicted in Table 1. The mechanical system is solved using the finite element Cast3m software35 and the behaviour law is implemented in the code generator MFront111,113,114.
The crack openings are estimated from the anelastic strain tensor \({\underline{\underline{\varepsilon }}}^{{{{\rm{ane}}}}}\) defined by:
where \({\underline{\underline{\sigma }}}^{{{{\rm{e}}}}}\) is the elastic part of the stress tensor. Normal crack aperture un is computed using the largest eigenvalues of the anelastic tensor \({\varepsilon }_{{{{\rm{I}}}}}^{{{{\rm{ane}}}}}\) and the mesh element characteristic length lc:
As mentioned above, the cement paste poroelastic properties required in Equation (1) are estimated using a micromechanics method, where the matrix is modelled through an equivalent C-S-H phase (comprising C-S-H solid phase and gel pores)13,85. In order to capture the decalcification effect of the C-S-H resulting from chemical degradation on the matrix properties, the evolution of the Young modulus of the binding C-S-H phase with the Ca/Si ratio follows the relation7:
where ECSH(1.6) and Egel are the Young modulus of the C-S-H phase with a Ca/Si ratio of 1.6 and of the amorphous silica gel corresponding to a totally decalcified phase, respectively.
Poisson ratio is assumed independent of the Ca/Si ratio and is taken as 0.25115; this allows calculating the bulk modulus kCSH of the C-S-H phase as a function of the Ca/Si ratio. These C-S-H properties are used to compute both shear gcp and bulk kcp moduli of the cement paste, and then its Young’s modulus, using the Mori-Tanaka scheme, which gives5,83,84,116:
where φi, gi and ki are the volume fraction, the shear modulus and the bulk modulus of phase i ∈ [1, Nph], respectively. The cement paste is assumed to be composed of Nph phases including portlandite, calcite, silica gel and capillarity pores. The volume fraction of the minerals is computed by Hytec. The volume fraction of the equivalent C-S-H \({\varphi }_{{{{\rm{CSH}}}}}^{eq}\) and the capillary porosity φcap are deduced from the total porosity ωm the volume fraction of C-S-H computed by Hytec, and the parameter γ, which represents the ratio of gel pore in the volume fraction of C-S-H13,85:
The shrinkage coefficient αξ used to compute the carbonation shrinkage (Equation (2)) and the Biot coefficient (Equation (1)) are calculated from the volumetric strain localization coefficient of the inclusive mineral phases:
with:
Numerical methodology
The numerical methodology rests on a Sequential Non Iterative coupling between Hytec and Cast3m. At each timestep, Hytec solves the heat transfer and the reactive flow problem34,77. The mechanic solver is called whenever the maximum evolution of porosity (over the whole domain) has gone over a user-defined threshold compared to the last mechanical solver call. Then, the hydrogeochemical data provided by Hytec are used to estimate the pore pressure Pm, the chemical strain tensor \({\underline{\underline{\varepsilon }}}^{\xi }\) and the poro-elastic properties of the geomaterial. These fields are used together with the damage value by Cast3m to compute the crack porosity ωc (Table 1). Then, the feedback towards the reactive flow problem is performed by adjusting the double porosity and its transport properties (Table 1) within the Hytec simulation. This approach constitutes a complete, thorough and dynamic two-way coupling between chemical and mechanical effects and is depicted in Fig. 6.
Data availability
All data generated or analysed during this study are included in this published article. More details about the experimental data and numerical methods can be found in cited references, mainly Kangni-Foli et al. 202166, Seigneur et al. 2018, 2020 and 202237,60,77. Cast3m is a publicly available mechanical code. Hytec software for this research is not publicly available due to intellectual and industrial property.
References
Steefel, C. I. & Lasaga, A. C. A coupled model for transport of multiple chemical species and kinetic precipitation/dissolution reactions with application to reactive flow in single phase hydrothermal systems. Am. J. Sci. 294, 529–592 (1994).
Steefel, C. I. Reactive transport at the crossroads. Rev. Mineral. Geochem. 85, 1–26 (2019).
Bildstein, O., Claret, F. & Frugier, P. Rtm for waste repositories. Rev. Mineral. Geochem. 85, 419–457 (2019).
Cama, J., Soler, J. M. & Ayora, C. Acid water-rock-cement interaction and multicomponent reactive transport modeling. Rev. Mineral. Geochem. 85, 459–498 (2019).
Ulm, J.-F., Constantinides, G. & Heukamp, F. H. Is concrete a poromechanics material? A multiscale investigation of poroelastic properties. Mat. Struct. 37, 43–58 (2004).
Seigneur, N., Mayer, K. U. & Steefel, C. I. Reactive transport in evolving porous media. Rev. Mineral. Geochem. 85, 197–238 (2019).
Stora, E., Bary, B., He, Q.-C., Deville, E. & Montarnal, P. Modelling and simulations of the chemo-mechanical behaviour of leached cement-based materials leaching process and induced loss of stiffness. Cem. Conc. Res. 39, 763–772 (2009).
Bary, B., Leterrier, N., Deville, E. & Le Bescop, P. A global strategy for solving reactive transport equations. Cem. Concr. Compos. 19, 70–83 (2014).
Miehe, C., Dal, H., Schanzel, L.-M. & Raina, A. A phase-field model for chemo-mechanical induced fracture in lithium-ion battery electrode particles. Int. J. Numer. Methods Eng. 106, 683–711 (2016).
Idiart, A., Lavinaa, M., Cochepin, B. & Pasteau, A. Hydro-chemo-mechanical modelling of long-term evolution of bentonite swelling. Appl. Clay Sci. 195, 105717 (2020).
Zhang, R., Xiong, Y., Winterfeld, P. H., Yin, X. & Wu, Y. A novel computational framework for thermal-hydrological-mechanical-chemical processes of co2 geological sequestration into a layered saline aquifer and a naturally fractured enhanced geothermal system. Greenhouse Gas Sci. Technoly 6, 370–400 (2016).
Stora, E., Bary, B., He, Q.-C., Deville, E. & Montarnal, P. Modelling and simulations of the chemo-mechanical behaviour of leached cement-based materials: Interactions between damage and leaching. Cem. Conc. Res. 40, 1226–1236 (2010).
Socié, A., Dubois, F., Monerie, Y., Neji, M. & Perales, F. Simulation of internal and external sulfate attacks of concrete with a generic reactive transport-poromechanical model. Eur. J. Environ. Civ. Eng. 0, 1–28 (2022).
Introïni, C., Sercombe, J., Ramière, I. & Le Tellier, R. Phase-field modeling with the taf-id of incipient melting and oxygen transport in nuclear fuel during power transients. J. Nucl. Mater. 556, 153173 (2021).
Krom, A. H. H., Koers, R. W. J. & Bakker, A. Hydrogen transport near a blunting crack tip. J. Mech. Phys. Solid. 47, 971–992 (1999).
Lesti, M., Tiemeyer, C. & Plank, J. CO2 stability of portland cement based well cementing systems for use on carbon capture & storage (CCS) wells. Cem. Conc. Res. 45, 45–54 (2013).
Salgues, M., Sellier, A., Multon, S., Bourdarot, E. & Grimal, E. DEF modelling based on thermodynamic equilibria and ionic transfers for structural analysis. Eur. J. Environ. Civ. Eng. 18, 377–402 (2014).
Sellier, A. & Multon, S. Chemical modelling of delayed ettringite formation for assessment of affected concrete structures. Cem. Conc. Res. 108, 72–86 (2018).
Manga et al. Changes in permeability caused by transient stresses: field observations, experiments, and mechanisms. Rev. Geophys. https://doi.org/10.1029/2011RG000382 (2012).
Yarushina, V. M. & Bercovici, D. Mineral carbon sequestration and induced seismicity. Geophys. Res. Lett. 40, 814–818 (2013).
Cox, S. F. Injection-driven swarm seismicity and permeability enhancement: Implications for the dynamics of hydrothermal ore systems in high fluid-flux, overpressured faulting regimes–an invited paper. Econ. Geol. 111, 559–587 (2016).
Vilarrasa, V., Carrera, J., Olivella, S., Rutqvist, J. & Laloui, L. Induced seismicity in geologic carbon storage. Solid Earth 10, 871–892 (2019).
Planel, D. et al. Experimental and Numerical Study on the Effect of Sulfates on Calcium Leaching of Cement Paste. https://framcos.org/FraMCoS-4/287.pdf (2001).
Yin, S., Dusseault, M. B. & Rothenburg, L. Coupled THMC modeling of CO2 injection by finite element methods. J. Petrol. Sci. Eng. 80, 53–60 (2011).
Zhang, R., Winterfeld, P. H., Yin, X., Xiong, Y. & Wu, Y. Sequentially coupled THMC model for CO2 geological sequestration into a 2D heterogeneous saline aquifer. J. Nat. Gas Sci. Eng. 27, 579–615 (2015).
Wu, D., Deng, T. & Zhao, R. A coupled THMC modeling application of cemented coal gangue-fly ash backfill. Constr. Build. Mater. 158, 326–336 (2018).
Zheng, L., Samper, J., Montenegro, L. & Fernández, A. M. A coupled THMC model of a heating and hydration laboratory experiment in unsaturated compacted febex bentonite. J. Hydrolo. 386, 80–94 (2010).
Idiart, A. E., López, C. M. & Carol, I. Chemo-mechanical analysis of concrete cracking and degradation due to external sulfate attack: a meso-scale model. Cem. Concr. Compos. 33, 411–423 (2011).
Zheng, L., Rutqvist, J., Xu, H. & Birkholzer, J. T. Coupled THMC models for bentonite in an argillite repository for nuclear waste: Illitization and its effect on swelling stress under high temperature. Eng. Geol. 230, 118–129 (2017).
Socié, A. Modélisation Chimio-mécanique De La Fissuration De Matériaux Cimentaires : Vieillissement Et Tenue Des Enceintes De Confinement Des Centrales Nucléaires (Université de Montpellier, 2019).
Rutqvist, J., Zheng, L., Chen, F., Liu, H. & Birkholzer, J. Modeling of coupled thermo-hydro-mechanical processes with links to geochemistry associated with bentonite-backfilled repository tunnels in clay formations. Rock. Mech. Rock. Eng. 47, 167–186 (2014).
Samper, J., Mon, A. & Montenegro, L. A coupled THMC model of the geochemical interactions of concrete and bentonite after 13 years of FEBEX plug operation. Appl. Geochem. 121, 104687 (2020).
Ma, Y., Chen, X., Hosking, L. J., Yu, H. & Thomas, H. R. THMC constitutive model for membrane geomaterials based on mixture coupling theory. Int. J. Solids Struct. 171, 103605 (2022).
van der Lee, J., De Windt, L., Lagneau, V. & Goblet, P. Module-oriented modeling of reactive transport with HYTEC. Comput. Geosci. 29, 265–275 (2003).
CEA. Cast3m Software (version 2021). http://www-cast3m.cea.fr/ (2021).
Xi, F. et al. Substantial global carbon uptake by cement carbonation. Nature Geosci. 9, 880–883 (2016).
Seigneur, N. et al. Predicting the atmospheric carbonation of cementitious materials using fully coupled two-phase reactive transport modelling. Cem. Conc. Res. 130, 105966 (2020).
Bary, B. & Sellier, A. Coupled moisture–carbon dioxide-calcium transfer model for carbonation of concrete. Cem. Conc. Res. 34, 1859–1872 (2004).
Nguyen, T., Bary, B. & de Larrard, T. Coupled carbonation-rust formation-damage modeling and simulation of steel corrosion in 3d mesoscale reinforced concrete. Cem. Conc. Res. 74, 95–107 (2015).
Cole, W. F. & Kroone, B. Carbonate minerals in hydrated Portland cement. Nature 184, BA57 (1959).
Mi, T. et al. Quantitative evaluation of cement paste carbonation using raman spectroscopy. Npj Mater. Degrad. 5, 1:35 (2021).
Dewaele, P. J., Reardon, E. J. & Dayal, R. Permeability and porosity changes associated with cement grout carbonation. Cem. Conc. Res. 21, 441–454 (1991).
Houst, Y. F. & Wittmann, F. H. Influence of porosity and water content on the diffusivity of CO2 and O2 through hydrated cement paste. Cem. Conc. Res. 24, 1165–1176 (1994).
Ngala, V. T. & Page, C. L. Effects of carbonation on pore structure and diffusional properties of hydrated cement pastes. Cem. Conc. Res. 27, 995–1007 (1997).
Claisse, P. A., El-Sayad, H. & Shaaban, I. G. Permeability and pore volume of carbonated concrete. ACI Mater. J. 96, 378–381 (1999).
Thiéry et al. Effect of carbonation on the microstructure and the moisture properties of cement-based materials. In Internation Conferance on Durability of Building Materials and Components, 1–8 (DBMC, 2011).
Morandeau, A., Thiéry, M. & Dangla, P. Impact of accelerated carbonation on OPC cement paste blended with fly ash. Cem. Conc. Res. 67, 226–236 (2015).
Jerga, J. Physico-mechanical properties of carbonated concrete. Constr. Build. Mater. 18, 645–652 (2004).
Chang, C. F. & Chen, J. W. Strength and elastic modulus of carbonated concrete. ACI Mater. J. 102, 315–321 (2005).
Ahmad, S. et al. Effects of carbonation pressure and duration on strength evolution of concrete subjected to accelerated carbonation curing. Constr. Build. Mater. 136, 565–573 (2017).
Zhang, H. et al. Elucidating the effect of accelerated carbonation on porosity and mechanical properties of hydrated Portland cement paste using X-ray tomography and advanced micromechanical testing. Micromachines 11, 471 (2020).
Zhan, B. J., Xuan, D. X., Poon, C. S. & Scrivener, K. L. Multi-scale investigation on mechanical behavior and microstructural alteration of C-S-H in carbonated Alite paste. Cem. Conc. Res. 144, 106448 (2021).
Xiao, J., Li, J., Zhu, B. & Fan, Z. Experimental study on strength and ductility of carbonated concrete elements. Constr. Build. Mater. 16, 187–192 (2002).
Tschegg, E. K., Bohner, E., Tritthart, J. & Müller, H. S. Investigations into fracture of carbonated concrete. Mag. Concr. Res. 63, 21–30 (2011).
Merah, A. & Krobba, B. Effect of the carbonatation and the type of cement (CEM I, CEM II) on the ductility and the compressive strength of concrete. Constr. Build. Mater. 148, 874–886 (2017).
Hunt, C. M. & Tomes, L. A. Reaction of hardened portland cement paste with carbon dioxide. J. Res. Nat. Bur. Stand.-A Phys. Chem. 66A, 473 (1962).
Šavija, B. & Luković, M. Carbonation of cement paste: Understanding, challenges, and opportunities. Constr. Build. Mater. 117, 285–301 (2016).
François, R., Laurens, S. and Deby, F.Corrosion and its Consequences for Reinforced Concrete Structures (Elsevier, 2018).
Georget, F., Prévost, J. H. & Huet, B. Impact of the microstructure model on coupled simulation of drying and accelerated carbonation. Cem. Conc. Res. 104, 1–12 (2018).
Seigneur, N., De Windt, L., Poyet, S., Socié, A. & Dauzères, A. Modelling of the evolving contributions of gas transport, cracks and chemical kinetics during atmospheric carbonation of hydrated C3S and CSH pastes. Cem. Conc. Res. 160, 106906 (2022).
Swenson, E. G. & Sereda, P. J. Mechanism of the carbonation shrinkage of lime and hydrated cement. J. App. Chem. 18, 111–117 (1968).
Houst, Y.F. Carbonation shrinkage of hydrated cement paste. In 4th CANMET/ACI International Conference on Durability of Concrete, 481–491, (ICDC, Australia,1997).
Suda, Y., Tomiyama, J., Saito, T. & Saeki, T. Effect of relative humidity on carbonation shrinkage and hydration product of cement paste (in Japanese). Cem. Sci. Conc. Tech. 73, 71–78 (2019).
Borges, P. H. R., Costa, J. O., Milestone, N. B., Lynsdale, C. J. & Streatfield, R. E. Carbonation of CH and C-S-H in composite cement pastes containing high amounts of BFS. Cem. Conc. Res. 40, 284–292 (2010).
Auroy, M. et al. Impact of carbonation on unsaturated water transport properties of cement-based materials. Cem. Conc. Res. 74, 44–58 (2015).
Kangni-Foli, E. et al. Carbonation of model cement pastes: the mineralogical origin of microstructural changes and shrinkage. Cem. Conc. Res. 144, 106446 (2021).
Richardson, I. G. The calcium silicate hydrates. Cem. Conc. Res. 38, 137–158 (2008).
Jennings, H. M. A model for the microstructure of calcium silicate hydrate in cement paste. Cem. Conc. Res. 30, 101–116 (2000).
Allen, A. J., Thomas, J. J. & Jennings, H. M. Composition and density of nanoscale calcium-silicate-hydrate in cement. Nat. Mater. 6, 311–316 (2007).
Qomi, M. J. A. et al. Combinatorial molecular optimization of cement hydrates. Nat. Commun. 5, 4960 (2014).
Chen, J. J., Thomas, J. J., Taylor, H. F. W. & Jennings, H. M. Solubility and structure of calcium silicate hydrate. Cem. Conc. Res. 34, 1499–1519 (2004).
Thomas, J. J., Chen, J. J., Allen, A. J. & Jennings, H. M. Effects of decalcification on the microstructure and surface area of cement and tricalcium silicate pastes. Cem. Conc. Res. 34, 2297–2307 (2004).
Geng, G., Myers, R. J., Qomi, M. J. A. & Monteiro, P. J. M. Densification of the interlayer spacing governs the nanomechanical properties of calcium-silicate-hydrate. Sci. Rep. 7, 10986 (2017).
Chen, J., Thomas, J. J. & Jennings, H. M. Decalcification shrinkage of cement paste. Cem. Conc. Res. 36, 801–809 (2006).
Šavija, B. & Luković, M. Carbonation of cement paste: understanding, challenges, and opportunities. Constr. Build. Mater. 117, 285–301 (2016).
Auroy, M. et al. Comparison between natural and accelerated carbonation (3% CO2): impact on mineralogy, microstructure, water retention and cracking. Cem. Conc. Res. 109, 64–80 (2018).
Seigneur, N., Lagneau, V., Corvisier, J. & Dauzères, A. Recoupling flow and chemistry in variably saturated reactive transport modelling—an algorithm to accurately couple the feedback of chemistry on water consumption and flow. Adv. Water Resour. 122, 355–366 (2018).
Van Genuchten, M. T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 44, 892–898 (1980).
Di Donato, G. & Blunt, M. J. Streamline-based dual-porosity simulation of reactive transport and flow in fractured reservoirs. Water Resour. Res. https://doi.org/10.1029/2003WR002772 (2004).
Samper, J., Zheng, L., Fernández, A. M. & Montenegro, L. Inverse modeling of multicomponent reactive transport through single and dual porosity media. J. Contam. Hydrolo. 98, 115–127 (2008).
Liu, M. & Mostaghimi, P. Reactive transport modelling in dual porosity media. Chem. Eng. Sci. 190, 436–442 (2018).
Nissan, A., Alcolombri, U., De Schaetzen, F., Berkowitz, B. & Jimenez-Martinez, J. Reactive transport with fluid-solid interactions in dual-porosity media. ACS ES&T Water 1, 259–268 (2020).
Bary, B. Simplified coupled chemo-mechanical modeling of cement pastes behavior subjected to combined leaching and external sulfate attack. Int. J. Numer. Anal. Meth. Geomech. 32, 1791–1816 (2008).
Socié, A., Monerie, Y. and Perales, F. Effects of the microstructural uncertainties on the poroelastic and the diffusive properties of mortar. J. Theor. Comput. Appl. Mech. https://doi.org/10.46298/jtcam.8849 (2022).
Pouya et al. Mineralogical evolution and expansion of cement pastes in a sulfate-confined environment. Minerals https://doi.org/10.3390/min13010001 (2023).
Mazars, J. A description of micro-and macroscale damage of concrete structures. Eng. Fracture Mech. 25, 729–737 (1986).
Martin, R.-P., Metalssi, O. O. & Toutlemonde, F. Importance of considering the coupling between transfer properties, alkali leaching and expansion in the modelling of concrete beams affected by internal swelling reactions. Constr. Build. Mater. 49, 23–30 (2013).
Cefis, N. & Comi, C. Chemo-mechanical modelling of the external sulfate attack in concrete. Cem. Conc. Res. 93, 57–70 (2017).
Sakata, K. A study on moisture diffusion in drying and drying shrinkage of concrete. Cem. Conc. Res. 13, 216–224 (1983).
Seigneur, N., Socié, A. and Mayer, K. U. A compositional global implicit approach for modeling coupled multicomponent reactive transport. Water Resour. Res. https://doi.org/10.1029/2021WR031774 (2023).
Matallah, M., La Borderie, C. & Maurel, O. A practical method to estimate crack openings in concrete structures. Int. J. Numer. Anal. Meth. Geomech. 34, 1615–1633 (2010).
Draup et al. Development of a novel damage model for concrete subjected to high temperature and constrain. In Proc. of the 25th Conference on Structural Mechanics in Reactor Technology (IASMiRT, 2019).
Jourdain, X. Etude Numérique Méso-macro Des Propriétés De Transfert Des Bétons Fissurés. https://hal.science/tel-01140869v1/file/Manuscrit_Xavier_Jourdain.pdf (2014).
Nilenius, F., Larsson, F., Lundgren, K. & Runesson, K. Mesoscale modelling of crack-induced diffusivity in concrete. Comput. Mech. 55, 359–370 (2015).
Blanc, P. et al. Thermoddem: A geochemical database focused on low temperature water/rock interactions and waste materials. Appl. Geochem. 27, 2107–2116 (2012).
Perko, J., Ukrainczyk, N., Šavija, B., Phung, Q. T. & Koenders, E. A. B. Influence of micro-pore connectivity and micro-fractures on calcium leaching of cement pastes-a coupled simulation approach. Materials (Basel) 13, 2697 (2020).
Socié, A., Dubois, F., Monerie, Y. & Perales, F. Multibody approach for reactive transport modeling in discontinuous-heterogeneous porous media. Comput. Geosci. 25, 1473–1491 (2021).
Wilson, W., Sorelli, L. & Tagnit-Hamou, A. Unveiling micro-chemo-mechanical properties of c-(a)-s-h and other phases in blended-cement pastes. Cem. Conc. Res. 107, 317–336 (2018).
Marquié, C., Richard, B., Dauzères, A. & Nahas, G. Concrete Aging in Containment Building and Deep Geological Disposal Facilities: the Odoba Project. https://irsn.hal.science/irsn-03517067 (2019).
Honorio, T., Bary, B. & Benboudjema, F. Multiscale estimation of ageing viscoelastic properties of cement-based materials: A combined analytical and numerical approach to estimate the behaviour at early age. Cem. Conc. Res. 87, 137–155 (2016).
Heinemann, N. et al. Enabling large-scale hydrogen storage in porous media-the scientific challenges. Energy Environ. Sci. 14, 853–864 (2021).
Brommundt, J., Kaempfer, T. U., Enssle, C. P., Mayer, G. & Wendling, J. Full-scale 3d modelling of a nuclear waste repository in the callovo-oxfordian clay. part 1: thermo-hydraulic two-phase transport of water and hydrogen. Geol. Soc. 400, 443–467 (2014).
Crusset, D. et al. Corrosion of carbon steel components in the french high-level waste programme: evolution of disposal concept and selection of materials. Corros Eng. Sci. Technol. 52, 17–24 (2017).
Rathnaweera, T. D., Wu, W., Ji, Y. & Gamage, R. P. Understanding injection-induced seismicity in enhanced geothermal systems: From the coupled thermo-hydro-mechanical-chemical process to anthropogenic earthquake prediction. Earth Sci. Rev. 205, 103182 (2020).
Galan, I., Andrade, C. & Castellote, M. Natural and accelerated CO2 binding kinetics in cement paste at different relative humidities. Cem. Conc. Res. 49, 21–28 (2013).
Drouet, E., Poyet, S., Le Bescop, P., Torrenti, J.-M. & Bourbon, X. Carbonation of hardened cement pastes: Influence of temperature. Cem. Conc. Res. 115, 445–459 (2019).
Djerbi, A., Bonnet, S., Khelidj, A. & Baroghelbouny, V. Influence of traversing crack on chloride diffusion into concrete. Cem. Conc. Res. 38, 877–883 (2008).
Hammood, M. N. A Meso-Macro Numerical Approach for Chloride Diffusivity Modeling : Taking into Account Chloride Binding and Crack Evolution in Concrete (Université de Nantes, 2017).
Millington, R. J. & Quirk, J. P. Permeability of porous solids. J. Chem. Soc. Faraday Trans. 57, 1200–1207 (1961).
Roth, S.-N., Léger, P. & Soulaïmani, A. A combined xfem-damage mechanics approach for concrete crack propagation. Comput. Methods Appl. Mech. Eng. 283, 923–955 (2015).
Gangnant, A. & Helfer, T. How to Implement the Fichant-la Borderie Damage Behaviour. https://tfel.sourceforge.net/FichantLaBorderieDamageBehaviour.html (2017).
Hillerborg, A., Modéer, M. & Petersson, P.-E. Analysis of crack formation and crack growth in concrete by means of fracture mechanics and finite elements. Cem. Conc. Res. 6, 773–781 (1976).
Helfer, T. et al. Introducing the open-source mfront code generator: application to mechanical behaviours and material knowledge management within the pleiades fuel element modelling platform. Comput. Math. Appl. 70, 994–1023 (2015).
Helfer, T. et al. The MFrontGenericInterfaceSupport project. J. Open. Sour. Softw. 5, 2003 (2020).
Haeckerd, C. J. et al. Modeling the linear elastic properties of portland cement paste. Cem. Conc. Res. 35, 1948–1960 (2005).
Mori, T. & Tanaka, K. Average stress in matrix and average elastic energy of materials with misfitting inclusions. Acta Metall. 21, 571–574 (1957).
Pignatelli, R., Comi, C. & Monteiro, P. J. M. A coupled mechanical and chemical damage model for concrete affected by alkali-silica reaction. Cem. Conc. Res. 53, 196–210 (2013).
Segura, J. M. & Carol, I. On zero-thickness interface elements for diffusion problems. Int. J. Numer. Anal. Meth. Geomech. 28, 947–962 (2004).
Acknowledgements
The project leading to this work has received funding from the European Union’s Horizon 2020 research and innovation programme under grant agreement n847593, in particular from the EURAD/MAGIC workpackage. We want to thank the Institut de Radioprotection et de Sureté Nucléaire (IRSN, France) and in particular Alexandre Dauzères for their participation in the data acquisition.
Author information
Authors and Affiliations
Contributions
The respective contributions of the different authors are listed here below A.S.: development, methodology, simulations, microtomographic images analysis, figure, writing and edition of the article N.S.: methodology, funding, supervision, simulations, figure, writing and edition of the article B.B.: methodology, funding, supervision, simulations, writing and edition of the article S.P.: supervision, microtomographic images analysis, experimental results, writing and edition of the article G.T.: microtomographic images analysis, writing and edition of the article.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing financial or non-financial interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Socié, A., Seigneur, N., Bary, B. et al. A fully coupled Hydraulic Mechanical Chemical approach applied to cementitious material damage due to carbonation. npj Mater Degrad 7, 60 (2023). https://doi.org/10.1038/s41529-023-00378-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41529-023-00378-x
- Springer Nature Limited