Abstract
The calculation of electron density distribution using density functional theory (DFT) in materials and molecules is central to the study of their quantum and macro-scale properties, yet accurate and efficient calculation remains a long-standing challenge. We introduce ChargE3Net, an E(3)-equivariant graph neural network for predicting electron density in atomic systems. ChargE3Net enables the learning of higher-order equivariant features to achieve high predictive accuracy and model expressivity. We show that ChargE3Net exceeds the performance of prior work on diverse sets of molecules and materials. When trained on the massive dataset of over 100K materials in the Materials Project database, our model is able to capture the complexity and variability in the data, leading to a significant 26.7% reduction in self-consistent iterations when used to initialize DFT calculations on unseen materials. Furthermore, we show that non-self-consistent DFT calculations using our predicted charge densities yield near-DFT performance on electronic and thermodynamic property prediction at a fraction of the computational cost. Further analysis attributes the greater predictive accuracy to improved modeling of systems with high angular variations. These results illuminate a pathway towards a machine learning-accelerated ab initio calculations for materials discovery.
Similar content being viewed by others
Introduction
Quantum mechanical interactions of electrons in atoms provide a foundation for understanding and predicting properties of materials1. Modern density functional theory (DFT), particularly the Kohn-Sham (KS) formulation of DFT2, is by far the most widely used method for performing such electronic structure calculations due to its balanced tradeoff between accuracy and computational cost. Because KS-DFT obtains the electronic structure by iteratively solving Kohn-Sham equations and re-calculating the electron charge density until convergence to a self-consistent field (SCF), extensive use of DFT is hindered by the unfavorable O(N3) scaling with the system size, making it infeasible for large-scale calculations beyond a few hundred atoms.
While prior works on linear-scaling DFT3,4,5, local coupled cluster methods6,7, and orbital-free formulation of DFT8 have nominally reduced the scaling limit, large-scale calculation is still unobtainable for general problems. In recent years, many efforts have focused on the potential of machine learning (ML) approaches to overcome the quantum scaling limit of DFT. ML models have been developed to map chemical and material systems to properties to enable high-throughput screening9,10,11,12,13,14. Once trained, ML models are computationally fast, but they are restricted to properties that already exist in a database (typically at the ground state), limiting their applicability to general problems. ML models have also been proven useful for predicting atomic energies and forces for large-scale molecular dynamic simulations15,16,17,18,19. The process generally requires a dedicated computational campaign with DFT to generate high-quality data for a subset of materials with a pre-defined potential or temperature range18,19,20,21,22,23,24. More recent work has trained a foundation model across the periodic table for predicting interatomic potentials25, but it still requires additional DFT data and model finetuning for applications beyond structure relaxation. An alternative approach is to directly predict converged DFT quantities (e.g., electron charge density) to reduce the number of SCF iterations needed to solve KS equations. Since the number of SCF iterations is dependent on the accuracy of the initialized charge density, a fast and accurate charge density prediction may be able to bypass the need for self-consistent iterations, enabling accurate computation of downstream properties at a fraction of the computational cost.
Several works have used ML for charge density prediction. One approach is to expand the charge density with a local atomic basis set and use ML to predict the expansion coefficients26,27,28,29,30,31,32. Local atomic orbital basis sets are often parametrized for specific elements. While these models are, in principle, more efficient, scaling on the order of the number of basis functions, they are restricted to the basis set they are trained on, thus impacting generalizability. Furthermore, any model that attempts to find the parameters of atomic basis sets that best fit grid-based data is fundamentally limited by the expressivity of the basis set32. A parallel line of research focuses on the prediction of the Hamiltonian operator33,34,35,36, however these are also restricted by the choice of basis set, and often not obtainable through DFT codes.
An alternative approach is to learn the electron charge density directly from a discretized grid of density points in 3D Cartesian space. The grid-based approach is agnostic to the basis set (plane-wave or atomic basis) used for the quantum chemistry calculation and are a natural input format for DFT codes37,38,39,40. Existing grid-based methods41,42,43,44,45 have shown promising results on small molecules and small subsets of material classes. Pioneering works41,42 have focused on learning the charge density using graph neural networks invariant to translation, rotation and permutation9,46. Jørgensen and Bhowmik42 later demonstrate an improvement in accuracy using an equivariant graph neural network, PaiNN43, through \({{\mathbb{R}}}^{3}\) vector representations and rotationally equivariant operations47. While these models have been shown to achieve high accuracy on small, specialized molecular or material datasets, no work has demonstrated applicability on larger, diverse datasets across the periodic table. In addition, these models use scalar and/or vector representations to construct rotationally equivariant networks, which could be further improved by incorporating higher-order equivariant features, as has been shown in other tasks, such as the prediction of atomic forces16. Finally, limited work has demonstrated the utility of ML-predicted charge densities to initialize DFT calculations, with existing work showing only marginal reduction of SCF steps44,48.
In this work, we develop a grid-based model, ChargE3Net, that uniquely combines graph neural networks, SO(3) equivariant features, and higher-order tensor operations, to accurately predict the electron charge density. Our model only uses atomic species and positions as input without the need for additional features. It enables the use of higher-order equivariant features to achieve more accurate performance and higher model expressivity. In a head-to-head comparison with prior grid-based and basis function-based methods, we show that our method not only achieves greater accuracy on existing benchmark data, but also is expressive enough to capture the complexity and variability present in Materials Project (MP) data49, consisting of more than 100K inorganic materials across the periodic table and for all materials classes. We demonstrate the application of MP-trained ChargE3Net to initialize DFT calculations, resulting in a median of 26.7% reduction in SCF steps on unseen MP data and 28.6% on novel GNoME materials50. Both have surpassed the reductions demonstrated by prior work44,48. When evaluating the utility of ChargE3Net in computing a wide range of electronic and thermodynamic properties non-self-consistently, we show a great portion of materials achieving near-DFT accuracy. Further analysis of materials with less accurate predictions provides insights into a potential cause of the observed inconsistency between self-consistent and non-self-consistent calculations to inform future research. By enabling higher-order equivariant models, we can also investigate the impact of equivariant representations in model performance. We show that higher-order representations yield more accurate charge density predictions for materials with high angular variation. Lastly, We demonstrate the linear time complexity of our model with respect to system size, showing the capability of predicting density on systems with > 104 atoms, surpassing what is feasible with ab initio calculations.
Results
Development of higher-order equivariant neural networks for charge density prediction
The charge density, along with other properties such as forces, is equivariant under rotation and translation of the atomic system. That is, a rotation or translation of the atomic system in Euclidean space will result in an equivalent rotation or translation to the charge density or forces. Formally, this is known as equivariance with respect to E(3), which includes rotations, translations, and reflections in 3D space. This can be achieved in principle by using only invariant scalar features46, such as inter-atomic distances; however, this prevents the model from using angular information, limiting the accuracy that can be attained51. More recent work47 has introduced equivariance methods using vector \({{\mathbb{R}}}^{3}\) features, such as relative atomic positions, to incorporate angular information, and has shown to improve the performance of charge density prediction43. We hypothesize that higher-order representations could help improve model performance and accelerate DFT calculations.
ChargE3Net achieves equivariance through means outlined by tensor field networks52. Translation equivariance is achieved by using relative atomic positions; rotation equivariance is achieved by restricting features to be irreducible representations, irreps, of SO(3), which are operated upon by equivariant functions. These features take the form \({V}_{cm}^{(\ell ,p)}\), a dictionary of tensors with keys representing rotation order ℓ ∈ {0, 1, 2, . . . } and parity p ∈ { − 1, 1}. Each tensor has a channel index c ∈ [0, Nchannels) and an index m ∈ [ − ℓ, ℓ]. In this way, the representation at a given rotation order ℓ and parity p would have a size of \({{\mathbb{R}}}^{{N}_{{{{\rm{channels}}}}}\times (2\ell +1)}\). These representations are combined with the equivariant tensor product operation ⊗ , using Clebsch-Gordan coefficients C52 as implemented in e3nn53:
where ℓo and po are given by ∣ℓ1 − ℓ2∣≤ℓo≤∣ℓ1 + ℓ2∣ and po = p1p2. We maintain only those representations with ℓo≤L where L is a maximum allowed rotation order. For ease of notation, we will omit the keys ℓ, p and indices c, m for these tensor representations for the rest of the paper. Unless otherwise indicated, we use an L = 4 maximum rotation order for ChargE3Net.
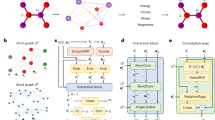
Figure 1 shows the model architecture of ChargE3Net. To predict charge density of a given atomic system, a set of M probe points \(\{{\vec{{{{\bf{g}}}}}}_{1},...,{\vec{{{{\bf{g}}}}}}_{M}\}\in {{\mathbb{R}}}^{3}\) are introduced to locations where charge densities are to be predicted. We represent predicted charge density \(\hat{\rho }(\vec{{{{\bf{g}}}}})\) as an equivariant graph neural network with inputs of atomic numbers \(\{{z}_{1},...,{z}_{N}\}\in {\mathbb{N}}\) with respective locations of the atoms \(\{{\vec{{{{\bf{r}}}}}}_{1},...,{\vec{{{{\bf{r}}}}}}_{N}\}\in {{\mathbb{R}}}^{3}\) where N denotes the total number of atoms, as well as probe locations \(\{{\vec{{{{\bf{g}}}}}}_{1},...,{\vec{{{{\bf{g}}}}}}_{M}\}\in {{\mathbb{R}}}^{3}\) and an optional periodic boundary cell \({{{\bf{B}}}}\in {{\mathbb{R}}}^{3\times 3}\) for periodic systems.
a Acceleration of DFT property prediction with ChargE3Net charge density initialization. b Illustration of single charge density probe point (center, gray) and its local environment within a periodic atomic system. c Sub-graph of local environment graph with atom nodes zi, zj and probe node gk. d Neural network architecture. Predicted charge density \(\hat{\rho }(\vec{{{{\bf{g}}}}})\) at probe point \({\vec{{{{\bf{g}}}}}}_{k}\) is computed from the atomic species zi, inter-atomic displacement vectors \({\vec{{{{\bf{r}}}}}}_{ij}\), and probe-atom displacement vectors \({\vec{{{{\bf{r}}}}}}_{ik}\) through a series of convolution and gate operations. e Convatom sends higher-order representations bidirectionally to atom nodes. Convprobe sends higher-order representations from atoms to probes.
As illustrated in Fig. 1b, c, a graph is first constructed with atoms and probe points as vertices, with edges formed via proximity with a cutoff of 4 Å. Edges connecting atoms are unidirectional and edges connecting atoms and probe points are directed pointing from atoms to probe points. Vertex features for atoms \({\{{{{{\bf{A}}}}}_{i}\}}_{i = 0}^{N}\) are initialized as a one-hot encoding of the atomic number, represented as an ℓ = 0, p = 1 tensor with Nchannels equal to the number of atomic species. Features for probe points \({\{{{{{\bf{P}}}}}_{k}\}}_{k = 0}^{M}\) are initialized as a single scalar zero (i.e., ℓ = 0, p = 1 and Nchannels = 1).
ChargE3Net uses a graph neural network (GNN) to update these tensor features (Fig. 1d). Within each layer of GNN, the network performs message passing between neighboring atoms and probes, where probe points can only receive messages from neighboring atoms (Fig. 1e). The core of the message passing in ChargE3Net is a convolution function that updates the vertex tensor feature with neighboring vertices by the convolution operation (Eq. (4) in “Methods” section). Since the proposed convolution operation replaces the linear message passing with equivariant operation through the tensor product defined in Eq. (1), the operation is rotation and translation equivariant; see “Methods” section for more detail.
ChargE3Net conducts a series of equivariant convolution and gate operations to obtain representations for each atom, with an addition series of equivariant convolution and gate operations to obtain representations for each probe point. The learned tensor feature associated to each probe point is passed to a post-processing layer where a simple regression is used to predict the charge density at the corresponding probe location \(\hat{\rho }({\vec{{{{\bf{g}}}}}}_{k})\).
Performance evaluation
We train and validate ChargE3Net on a diverse set of DFT-computed charge density data, including organic molecules (QM9)54,55,56, nickel manganese cobalt battery cathode materials (NMC)57, and inorganic materials collected from Materials Project (MP)49,58. The first two datasets have been used in the past for benchmarking charge density models for small molecules and a subset of crystal systems with boundary conditions30,43. To develop a charge density model for the entire periodic table, we investigate one of the largest open databases of DFT, the Materials Project (MP) database. It includes charge densities for over 100K bulk materials with diverse compositions and structures (Supplementary Figs. 1–3 and “Methods” section).
We assess the performance our models using mean absolute error normalized by the total number of electrons within a volume of the atomic system27,28,30,43, εmae, which is computed via numerical integration on the charge density grid points G:
Unless otherwise noted, the probe points G hereby reference the full set of discretized unitcell grid points for which we have DFT-computed charge density values.
Table 1 compares the performance of ChargE3Net to models introduced in OrbNet-Equi30 and DeepDFT43. For QM9 and NMC datasets, we use identical training, validation, and test splits as Jørgensen and Bhowmik43. All reported εmae are computed using publicly released models and verified to match the numbers reported in the original work. For the MP dataset, we train the DeepDFT models using the same experimental settings from the original work (see Supplementary Note 1 for more detail). We observe that all equivariant models perform better than invariant models, demonstrating the importance of respecting rotation equivariance. Moreover, ChargE3Net model significantly outperforms prior equivariant DeepDFT models43 on the Materials Project (MP) and QM9 datasets, while achieving similar performance on the NMC dataset. This suggests that the inclusion of higher-order representations can improve model performance. More remarkably, our model achieves a lower εmae on the QM9 dataset than OrbNet-Equi30 model, which leverages additional features based on quantum mechanical calculations while ChargE3Net only uses atomic species and position information. This shows how the model is capable of learning highly informative representations of quantum interactions in a purely data-driven approach.
ChargE3Net’s performance on the MP data demonstrates that it is capable of successfully modeling charge density across the periodic table and a wide variety of material classes that are not present in other datasets. When we compare the prediction performance with respect to the number of unique species in a material, the MP-trained ChargE3Net is capable of predicting charge density in systems with many unique species, without a significant change in error distribution as number of species increases (Supplementary Fig. 4). This suggests ChargE3Net can reproduce a broad range of chemical interactions at the electronic level without incurring the cost of an ab initio calculation.
Using predicted charge densities to accelerate DFT
DFT calculations require an initial charge density and wavefunction prior to iteratively solving the Kohn-Sham equations until self-consistency59. Charge density initializations that closely match the ground-state charge density often save compute time by reducing the number of self-consistent field (SCF) steps needed to find a self-consistent solution. Many schemes for initializing the charge density exist in the literature, but the most common one is the superposition of atomic densities (SAD), where the initial charge density is computed by summing over the atomic charge density of each atom in the system60.
We demonstrate that charge densities predicted by ChargE3Net reduce the number of SCF steps, thereby accelerating DFT calculations, on unseen non-magnetic materials (Fig. 2a, b) compared to a SAD initialization. The median number of SCF steps needed to converge a single-point calculation self-consistently for a non-magnetic material starting from the SAD initialization is 15, while the same starting from a ChargE3Net initialization is 11, representing a 26.7% decrease in SCF steps. As an upper-bound baseline, we also include the distribution of the number of SCF steps needed to converge a calculation starting from a converged (i.e. ground-truth) charge density (SC), showing that our model still has room for improvement. About 96% of calculations done with a predicted charge density ran with fewer SCF steps than initializing with SAD, and the compute time improvement is robust to a wide range of εmae (Supplementary Fig. 5).
Comparison of DFT calculations initialized from superposition of atomic densities (SAD), ChargE3Net predictions, and ground-truth densities from existing self-consistent calculations (SC). a Average number of SCF steps required to converge the total energy to 5 × 10−5 eV atom−1 for non-magnetic materials in the MP test set, with respect to the number of unique species within each material. Error bar shows ± one standard error. b Number of steps required for self-consistent (SC) and non-self-consistent (NSC) calculations. Box-plots show median as center line, upper and lower quartiles as box limits, 1.5x interquartile range as whiskers, and outliers as points. c Non-self-consistent physical property calculations for total energy, atomic forces, band energies, and band gaps. Dashed lines indicate chemical accuracy (1 meV atom−1 for per-atom energies, 0.03 eV Å−1 for forces, and 43 meV for band energies and band gap). Errors of exactly zero are replaced with 10−8 for visualization purposes. Interior of violin-plots shows median as center line, upper and lower quartiles as box limits, and 1.5x interquartile range as whiskers. d Percentage of materials achieving chemical accuracy for non-self-consistent calculations.
To evaluate how well ChargE3Net’s predicted charge densities reproduce physical properties, we compute the energy, forces, band energies, and bandgaps of the test set non-self-consistently (Fig. 2c, d). 40% of materials in the test set have per-atom energy errors less than 1 meV atom−1. 70% of materials have forces <0.03 eV Å−1, a common threshold for structural relaxations; 15% of the test set have force errors of 0.0 (Supplementary Fig. 6). All of the structures with perfect agreement have self-consistent forces of 0.0 eV Å−1 for each atom and Cartesian component, possibly because of cancellation of charge density errors due to symmetry. 45% and 76% of materials recover band energies at each k-point and the direct band gap within chemical accuracy (43 meV), respectively. 45% of the band gaps obtained non-self-consistently exactly matched those of self-consistent calculations (Supplementary Fig. 6). Similar to the force data described above, calculations with perfect agreement all have a self-consistent band gap of 0 eV, indicating the model is able to readily identify metallic materials. We note that our use of chemical accuracy for band gaps is a more stringent criterion than experimental measurement errors for well-studied semiconductors61. In addition, non-self-consistent calculations using the Materials Project parameters as done with this test set have an additional source of error (Supplementary Fig. 7 and “Methods” section) as a result of an incorrect calculation parameter set by the Materials Project. This error could explain why not all NSC calculations computed on a self-consistent charge density achieve chemical accuracy (see Fig. 2d and Supplementary Fig. 8).
To examine the generalization capabilities of ChargE3Net on out-of-distribution data, we analyze a random subset of 1924 materials published by GNoME50 with 5 or more unique species to differentiate it from the MP distribution. The average εmae found for this set is 0.632%, which is higher than that of the MP test set for ChargE3Net but lower than either DeepDFT variant trained on the Materials Project (Table 1). We conduct a similar experiment to the MP test set above with non-self-consistent DFT calculations on 1510 non-magnetic materials. The median energy error is 4.3 meV atom−1 for the GNoME set, whereas the same is 1.8 meV atom−1 for the MP test set. Only 8.4% of materials in GNoME computed non-self-consistently from the ChargE3Net charge density obtained the total energy within chemical accuracy (<1 meV atom−1), though nearly all self-consistent calculations meet this criteria (Supplementary Fig. 9). The median number of SCF steps needed for self-consistency falls from 14 to 10 steps when initializing with ChargE3Net, a 28.6% drop (Supplementary Fig. 10) and a similar acceleration found for the Materials Project test set. Moreover, 91% of calculations saw a decreased number of SCF steps to reach convergence. While further work is needed to improve the generalizability of ChargE3Net for non-self-consistent property predictions, self-consistent calculations on out-of-distribution materials are still accelerated when initialized by the predicted charge density.
In addition to the model’s robustness to materials outside its training set, we show that ChargE3Net can predict the charge densities of materials after small atomic perturbations with minor increase to the charge density error (Supplementary Fig. 11). This allows us to accurately obtain phonon properties, which may rely on finite differences as the main method to obtain approximations to the local potential energy surface, from non-self-consistent calculations. We compute the constant-volume heat capacity (Cv) under the harmonic approximation for two zeolites, which are not included in the Materials Project dataset, and show that Cv(T) obtained closely match those obtained by self-consistent calculations (Supplementary Note 2). As another example of transferability, we compute the electronic bandstructure of the Si(111)-2 × 1 surface non-self-consistently from the ChargE3Net prediction and show that it almost exactly matches that of a self-consistent calculation (Supplementary Note 3).
Higher-order representations lead to improved model accuracy
To demonstrate the impact of introducing higher-order equivariant tensor representations in our model, we examine the effect of training models while varying the maximum rotation order L, with ℓ ∈ {0, . . . , L} up to L = 4 used in the final model. We determine the number of channels for each rotation order by \({N}_{{{{\rm{channels}}}}}=\lfloor \frac{500/(L+1)}{\ell * 2+1}\rfloor\). For example, the L = 0 model has representations consisting of 500 even scalars, and 500 odd scalars, while the L = 1 model has representations consisting of 250 even scalars, 250 odd scalars, 83 even vectors, and 83 odd vectors. In this way, each model is constructed such that the total representation size and the proportion of the total representation used by each rotation order are approximately equal. We train each model on 1000 and 10,000 material subsets and the full MP dataset, using the same validation and test sets. We observe a consistent increase in performance on each training subset as the maximum rotation order increases, and a similar scaling behavior with respect to the training set size (Supplementary Fig. 12). This trend suggests that higher-order representations are necessary for accurate charge density modeling, and can match the performance of lower order models with less data.
To gain intuition behind why and when higher-order representations yield higher performance, we investigate two factors contributing to the variance of charge density within a material: (1) radial dependence, or a dependence on the distance from neighboring atoms, and (2) angular dependence, or dependence on angular orientation with respect to those atoms and the larger atomic system. While most materials exhibit strong radial dependence, some also exhibit strong angular dependence. For example, materials with covalent bonds share electrons between nuclei, leading to higher charge density along bonding axes and more angular dependence. In Fig. 3, we illustrate this concept with two materials. Cs(H2PO4) exhibits high angular dependence, where charge density is dependent on angle as well as radial distance from the nearest atom. The complex nature of the charge density shown here arises from covalent bonding among the H, P, and O atoms. Conversely, Rb2Sn6 does not exhibit this, as its density appears to be almost entirely a function of the atomic distance, suggesting that a lower-order equivariant or invariant architecture could model its electron density well. This may be indicative of ionic interactions rather than the covalent interactions found in Cs(H2PO4). We find this intuition to be consistent with model performance, as Fig. 3 shows similar performance for L = 0 and L = 4 models for Rb2Sn6, while the L = 4 model exceeds the performance of the L = 0 model for Cs(H2PO4).
Comparison of materials with high and low angular variance. a Material Cs(H2PO4) with high angular variance. b Material Rb2Sn6 with low angular variance. Left to right: visualization of charge density isosurfaces (gray); plot of DFT-computed charge density with respect to radial distance from nearest atom; εmae for ChargE3Net model predictions on these materials.
At the atomic level, we find more evidence of the benefits of higher-order equivariant representations in modeling charge density. We examine the per-element errors by computing εmae on grid points Glocal,i ⊂ G, a set of points that are within 2Å of an atom of species i. Fig. 4 shows this per-element error for both L = 0 (lower-left triangles) and L = 4 (upper-right triangles), averaged across the test set. While the L = 0 model struggles with reactive non-metals and metalloids, which often form covalent bonds, L = 4 shows strong improvement among these elements. Nearly all elements show improvement, but the median change in εmae values for those materials containing a non-metal or metalloid is −44.6% (n = 1628) compared to −23.0% for materials with only metals (n = 346; Supplementary Fig. 13).
The lower-left triangles indicate the average εmae per element at L = 0, and the upper right triangles represent εmae per element at L = 4. Performance improvements are shown across the periodic table. Values are computed over the set of grid points Glocal, and averaged across all materials containing those elements in the test set. Only elements in at least 10 test set materials are shown.
To further quantify angular dependence within the system, we develop a metric ζ to determine to what extent a particular system exhibits more angular variation in its charge density with respect to atom locations. This is achieved by measuring the dot product of the unit vector from a probe point to its nearest neighboring atom and the gradient of the density at that probe point:
where G is a set of probe points and \({\hat{{{{\bf{r}}}}}}_{ki}\) is a unit vector from probe point at location \({\vec{{{{\bf{g}}}}}}_{k}\) to the closest atom at location \({\vec{{{{\bf{r}}}}}}_{i}\). Intuitively, a material with charge density gradients pointing directly towards or away from the nearest atom will have dot products larger in magnitude and ζ → 0, whereas a material with density that has high angular variance with respect to the nearest atom will have dot products smaller in magnitude, and ζ → 1; see Supplementary Fig. 14 for the test set average ζ over Glocal,i for every element. We observe that the differences in performance between the lower and higher rotation order networks correlates strongly with ζ (Supplementary Fig. 15). With covalent bonding and associated high angular variance frequently present in the Materials Project data, this further justifies the need for introducing higher rotation order representations into charge density prediction networks. In addition, we find the higher-order model maintains higher accuracy under perturbations to atomic positions (Supplementary Fig. 11), an imperative trait when using models for phonon calculations.
Runtime and scalability
To demonstrate the scalability of our model, we analyze the runtime duration of our model on systems with increasing number of atoms, and compare to the duration of DFT calculations. We run each method on a single material, BaVS3 (mp-3451 in MP), creating supercells from 1 × 1 × 1 to 10 × 10 × 10 and recording the runtime to generate charge density of the system. Supplementary Fig. 16 shows an approximate linear, O(N), scaling of our model with respect to number of atoms, while DFT exhibits approximately O(N2.3) before exceeding our computational budget. This is to be expected, as the graph size increases linearly with cell volume if the resolution remains the same, while DFT has shown to scale at a cubic rate with respect to system size43. Furthermore, our method can be fully parallelized up to each point in the density grid with no communication overhead.
Discussion
This work introduces ChargE3Net, an architecture for predicting charge density through equivariance with higher-order representations. We demonstrate that introducing higher-order tensor representations over scalars and vectors used in prior work achieves greater predictive accuracy, and show how this is achieved through the improved modeling of systems with high angular variance. ChargE3Net enables accurate charge density calculations on atomic systems larger than what is computationally feasible with DFT, but can also be used in combination with self-consistent DFT to reduce the number of SCF steps needed for convergence. Our findings hold across the large and diverse Materials Project dataset, paving the way towards a universal charge density model for materials. Future work to expand the model to charge density calculations of unrelaxed structures such as those in MPtrj24 would support general application of ML models to accelerate ab initio calculations and should be pursued.
The work of Hohenberg and Kohn proves that all material properties could, in principle, be derived from the electron density1. Because this quantity is so fundamental to predicting material properties, we view models that compute electron densities as a potential intermediate towards other material properties that may improve the generalizability of machine learning models in material science. As evidence, our non-self-consistent calculations, which can be seen as a ground-truth calculation of the electronic strucuture (and derived properties) using the crystal structure and charge density as inputs, demonstrate that one could indeed obtain electronic and thermal properties of materials using highly accurate charge-density estimates. On a broader dataset, we show that non-self-consistent calculations are able to capture the total energy, atomic forces, electronic bandstructure, and the band gap within chemical accuracy for a majority of structures in the test set, though there is room for improvement. This leads us to believe that large models trained on a charge density dataset that spans the known material space could be a promising direction towards a foundation model for DFT calculations that can be fine-tuned for downstream property prediction.
We have also explored the connection between errors in charge density predictions and the property error. We show in Supplementary Figs. 17–22 that errors in the charge density establish a lower bound to the property error, and that small charge density errors can give rise to substantial property error. Examining charge density errors more closely, specifically analyzing εmae localization in low- and high-error non-self-consistent calculations, we find difficulty identifying localized regions where charge density prediction errors lead to property errors (Supplementary Fig. 23). While the errors in non-self-consistent property predictions are certainly affected by errors in charge density predictions from ChargE3Net, the errors may in part be explained by an incorrect DFT setting (the VASP tag LMAXMIX. See the Methods section for more information). The errors introduced by this calculation parameter may mean achieving chemical accuracy is improbable for some materials using non-self-consistent calculations even when initializing with a self-consistent (i.e. ground truth) charge density.
We demonstrate that higher-order E(3) equivariant tensor operations yield significant improvement in charge density predictions and are more data efficient (Figs. 3 and 4). However, the E(3) convolution used in this work are limited by the O(L6) time complexity of tensor products62. Recent work62 has showed that SO(3) convolutions can be reduced to SO(2), with a time complexity of O(L3). In the future, our approach can be combined with the methodology presented in62 to improve computational efficiency, and enable the practical usage of higher rotation orders (L > > 4) in atomistic modeling.
We also anticipate extending our model to include the spin density, which will allow for acceleration of DFT calculations of magnetic materials. Training ChargE3Net with energies and forces would allow for rapid identification of the lowest energy magnetic configuration, a normally laborious and time-intensive process63,64, and the ability to obtain magnetic properties, such as the Curie temperature.
Methods
ChargE3Net architecture
As described in Section 2.1, the inputs of the model consist of probe coordinates \(\vec{{{{\bf{g}}}}}\) and atom coordinates \(\vec{{{{\bf{r}}}}}\) with species z. Each atom and probe point are represented by a dictionary of tensors, where An denotes an atom representation and Pn denotes a probe representation, each at layer n. An=0 is initialized as a one-hot encoded z, represented as an ℓ = 0, p = 1 tensor with Nchannels equal to the number of atomic species. Pn=0 is initialized as single scalar zero, with ℓ = 0, p = 1, and Nchannels = 1. Each representation is updated through a series of alternating convolution Conv(⋅) and non-linearity Gate(⋅) layers, a total of Ninteractions = 3 times. With each convolution layer, all possible outputs of the tensor product at different ℓ and p values with ℓo≤L are concatenated, increasing the representation size past the scalar initializations of An and Pn. Atom representations are updated with \({{{{\bf{A}}}}}_{i}^{n+1}=\,{{\mbox{Gate}}}({{{\mbox{Conv}}}\,}_{{{{\rm{atom}}}}}^{n}({\vec{{{{\bf{r}}}}}}_{i},{{{{\bf{A}}}}}_{i}^{n}))\). Convatom is defined as:
where W1, W2, W3 are learned weights applied as a linear mix or self-interaction52. The set N(i) includes all atoms within the cutoff distance, including those outside potential periodic boundaries. rij is the distance from \({\vec{r}}_{i}\) and \({\vec{r}}_{j}\), with unit vector \({\hat{r}}_{ij}\). \(Y({\hat{{{{\bf{r}}}}}}_{ij})\) are spherical harmonics, and \(R({r}_{ij})\in {{\mathbb{R}}}^{{N}_{{{{\rm{basis}}}}}}\) is a learned radial basis function defined as:
where MLP(⋅) is a two-layer multilayer perceptron with SiLU non-linearity65, ϕ(⋅) is a Gaussian basis function \(\phi {({r}_{ij})}_{k}\propto \exp (-{({r}_{ij}-{\mu }_{k})}^{2})\) with μk uniformly sampled between zero and the cutoff, then normalized to have a zero mean and unit variance.
The convolution updates the representation of each atom to be the sum of tensor products between neighboring atom representations and the corresponding spherical harmonics describing their relative angles, weighted by a learned radial representation. This sum is followed by an additional self-connection, then a residual self-connection. The output of the convolution is then passed though an equivariant non-linearity Gate( ⋅ ) operation as described in ref. 66. We use SiLU and \(\tanh\) activation functions for even and odd parity scalars respectively, as is done in16.
Probe representations are updated similarly as the atoms for each layer, except their representations depend solely on the representations of neighboring atoms, with no probe-probe interaction. Each probe representation is updated with \({{{{\bf{P}}}}}_{k}^{n+1}=\,{{\mbox{Gate}}}({{{\mbox{Conv}}}\,}_{{{{\rm{probe}}}}}^{n}({\vec{{{{\bf{g}}}}}}_{k},{{{{\bf{P}}}}}_{k}^{n}))\), where Convprobe is defined as:
Note that weights W are not shared with those for \({\,{{\mbox{Conv}}}\,}_{{{{\rm{atom}}}}}^{n}(\cdot )\). Since atom representations are computed independently of probe positions, they can be computed once per atomic configuration, even if multiple batches are required to obtain predictions for all probe points. Finally, predicted charge density \(\hat{\rho }({\vec{{{{\bf{g}}}}}}_{k})\) is computed as a linear combination of the scalar elements of the final representation \({{{{\bf{P}}}}}_{k}^{n = {N}_{{{{\rm{layers}}}}}}\).
Training ChargE3Net models
We develop an algorithm to achieve more efficient atom-probe graph construction, enabling faster training and inference times. Prior work constructs graphs by adding probe points directly to the atomic structure, computing edges with atomic simulation software such as ase or asap67, then removing edges between probes. While this is performant for small systems with few probes, we find it does not scale well due to the redundant computation of probe-probe edges, which grow quadratically with respect to the number of probe points. To address this, our algorithm leverages two k-d trees68; one to partition atoms, and one to partition probe points. This enables an efficient radius search for atom-probe edges exclusively. We implement this through modification of the k-d tree implementation from scipy69 to handle periodic boundary conditions. Constructing graphs with 1000 probe points, we observe an average graph construction time ( ± standard error) of 0.00758 ± 0.00087, 0.0103 ± 0.0005, and 0.00462 ± 0.00056 seconds for MP, QM9, and NMC respectively. This is at least an order of magnitude faster than methods from ref. 43, with which we measured graph construction times of 12.6 ± 0.9, 0.114 ± 0.006, and 0.141 ± 0.010 s.
To train the ChargE3Net model, Supplementary Table 1 outlines the experimental setup on each of the datasets (e.g., learning rate, batch size, number of probe points and number of training steps). Specifically, at each gradient step, a random batch of materials is selected, from which a random subset of Npoints probe points are selected. We use the Adam optimizer70, and decay the learning rate by 0.96s/β at step s. We find that optimizing for L1 error improves performance and training stability over mean squared error (Supplementary Table 2). Supplementary Fig. 24 shows the evolution of training loss and validation error as the model is trained on each dataset. All models were implemented in PyTorch and trained on NVIDIA Volta V100 GPUs using a distributed compute architecture.
Datasets
The QM9 and NMC datasets, along with train, validation and test splits, are provided by Jørgensen and Bhowmik43. The QM9 dataset56 contains VASP calculations of the 133,845 small organic molecules introduced by Ramakrishnan et al.55, with training, validation, and test splits of size 123,835, 50, and 10,000 respectively. The NMC dataset57 consists of VASP calculations of 2000 randomly sampled nickel manganese cobalt oxides containing varying levels of lithium content, with training, validation, and test splits of size 1450, 50, and 500 respectively. For the MP data, we collected 122,689 structures and associated charge densities from api.materialsproject.org49. Structures in the dataset that shared composition and space group were identified as duplicates and only the highest material_id structure was included, leaving 108,683 materials. The data was split randomly into training, validation, and test splits with sizes 106,171, 512, and 2000 respectively. Later, analyzing the test set materials for thermodynamic stability and structural abnormalities (Supplementary Fig. 25), 26 materials were found to have unrealistic volume per atom, in excess of 100 Å3 atom−1 and mostly from space group Immm. These materials were removed from the test set and excluded from all reported results and figures.
We note to the reader a known issue with the Materials Project dataset. Original calculation parameters may have an incorrectly set VASP parameter called LMAXMIX, which sets the maximum angular momentum number for the one-center PAW charge densities saved in the charge density output of VASP and passed into the charge density mixer. This affects elements with d- and f-electrons when no Hubbard U parameter was set by the Materials Project. In Supplementary Fig. 7, we correct this error for the randomly sampled test set, then compare the distribution of properties between non-self-consistent calculations of the original and corrected input parameters. Note that non-self-consistent calculations with a potentially incorrectly set LMAXMIX, as is set in the current Materials Project charge density dataset, makes a per-atom energy error about two orders of magnitude larger than that of self-consistent calculations. This represents an additional source of error to all non-self-consistent calculations based on Materials Project data.
In addition to a held-out test set randomly sampled from the Materials Project, we obtain a random set of 2000 published structures from GNoME50 as a second test set. Specifically, we choose a random set of materials from GNoME with 5 or 6 unique species as these are less well-represented in the Materials Project training data. DFT calculations were set up using pymatgen71 and otherwise using the same methodology as detailed in Section 4.4. 76 calculations failed, leaving 1924 materials for analysis, 1510 of which were non-magnetic. Non-magnetic structures were identified via DFT calculations initialized by SAD and magnetic moment guesses provided by pymatgen with an overall absolute magnetic moment <0.1 μB and absolute atomic magnetic moments <0.1 μB for every atom in the structure.
Supplementary Figure 1 shows a visualization of SOAP descriptors of materials in the MP train and test set and GNoME subset, projected into 2-d using t-SNE. We do not find a significant difference in distributions across the MP train and test sets, which is to be expected as the data is divided randomly. Supplementary Figure 2 shows the distribution of crystal systems and space groups within the MP training set. As seen with the SOAP descriptors, in Supplementary Fig. 3 we note a similar distribution of crystal systems across the MP train and test sets, with the GNoME subset showing significantly more monoclinic systems and significantly fewer tetragonal and cubic systems.
Density functional theory calculations
All density functional theory (DFT) calculations were done with VASP version 5.4.437,38,39,72 using projector-augmented wave (PAW) pseudopotentials73. For all calculations done on the test set of Materials Project data, we use the input files provided by the Materials Project to ensure these are computed in a manner consistent with how the charge density grids are originally generated. For the GNoME dataset, we use a k-point density of 100 points Å3, the same density that the original Materials Project charge density dataset was computed with, and generated the input files with pymatgen71. We set LMAXMIX to 4 for d-elements and 6 for f-elements only for DFT+U calculations as set by pymatgen, which, while incorrect (see Section 4.3), allows us to compare our performance on this set of materials against that of the Materials Project test set. For the experiments with perturbed structures, including those where electronic and thermal properties were computed, we use all the same settings as the Materials Project but with different k-grids, all generated with the Monkhorst-Pack scheme unless otherwise specified. We use a 520 eV energy cutoff and converge each calculation until the change in energy between SCF steps is less than 10−5 eV. For the Si(111)-(2 × 1) calculation, we use a k-grid of 4 × 8 × 1, while all zeolite calculations were done at the gamma-point only. Electronic bandstructures were plotted using pymatgen71. We use the same Hubbard U values as the Materials Project, which were obtained from Wang et al.74 and Jain et al.75. PAW augmentation occupancies were not predicted by ChargE3Net and were taken from the Materials Project dataset or computed self-consistently for the GNoME dataset.
Thermal properties were computed using phonopy76,77 for the heat capacity. Zeolite and bulk Si structures were relaxed until the maximum norm of the Hellmann-Feynman forces fell below 0.001 eV Å−1 prior to computing thermal properties. Structures were perturbed by 0.03Å to find the Hessian of the potential energy surface via finite differences, and the heat capacity at constant volume can then be found via the harmonic approximation with the equation
where θk = hνk/kB, h is Planck’s constant, νk is the vibrational frequency of vibrational mode k, kB is Boltzmann’s constant, R is the gas constant, and T is the temperature in Kelvin.
Data availability
Materials Project data was collected on 7 May 2023. Associated task identifiers will be included in our provided repository, along with the necessary download script, and our train, validation, and test splits. We also provide the identifiers for the subset of GNoME data used in our work. VASP computations on the QM9 and NMC datasets were downloaded from refs. 56 and 57 respectively.
Code availability
Our model implementation, along with pretrained model weights is available at https://github.com/AIforGreatGood/charge3net.
References
Hohenberg, P. & Kohn, W. Inhomogeneous electron gas. Phys. Rev. 136, B864–B871 (1964).
Kohn, W. & Sham, L. J. Self-consistent equations including exchange and correlation effects. Phys. Rev. 140, A1133–A1138 (1965).
Prentice, J. C. A. et al. The ONETEP linear-scaling density functional theory program. J. Chem. Phys. 152, 174111 (2020).
Soler, J. M. et al. The SIESTA method for ab initio order-N materials simulation. J. Condens. Matter Phys. 14, 2745 (2002).
Mohr, S. et al. Accurate and efficient linear scaling DFT calculations with universal applicability. Phys. Chem. Chem. Phys. 17, 31360–31370 (2015).
Riplinger, C. & Neese, F. An efficient and near linear scaling pair natural orbital based local coupled cluster method. J. Chem. Phys. 138, 034106 (2013).
Riplinger, C., Sandhoefer, B., Hansen, A. & Neese, F. Natural triple excitations in local coupled cluster calculations with pair natural orbitals. J. Chem. Phys. 139, 134101 (2013).
Witt, W. C., del Rio, B. G., Dieterich, J. M. & Carter, E. A. Orbital-free density functional theory for materials research. J. Mater. Res. 33, 777–795 (2018).
Xie, T. & Grossman, J. C. Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties. Phys. Rev. Lett. 120, 145301 (2018).
Chen, C., Ye, W., Zuo, Y., Zheng, C. & Ong, S. P. Graph networks as a universal machine learning framework for molecules and crystals. Chem. Mater. 31, 3564–3572 (2019).
Louis, S.-Y. et al. Graph convolutional neural networks with global attention for improved materials property prediction. Phys. Chem. Chem. Phys. 22, 18141–18148 (2020).
Dunn, A., Wang, Q., Ganose, A., Dopp, D. & Jain, A. Benchmarking materials property prediction methods: the Matbench test set and Automatminer reference algorithm. Npj Comput. Mater. 6, 1–10 (2020).
Choudhary, K. & DeCost, B. Atomistic line graph neural network for improved materials property predictions. Npj Comput. Mater. 7, 185 (2021).
Koker, T., Quigley, K., Spaeth, W., Frey, N. C. & Li, L. Graph contrastive learning for materials. Preprint at https://arxiv.org/abs/2211.13408 (2022).
Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Phys. Rev. B 99, 014104 (2019).
Batzner, S. et al. E (3)-Equivariant graph neural networks for data-efficient and accurate interatomic potentials. Nat. Commun. 13, 2453 (2022).
Musaelian, A. et al. Learning local equivariant representations for large-scale atomistic dynamics. Nat. Commun. 14, 579 (2023).
Chmiela, S. et al. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 3, e1603015 (2017).
Du, X. et al. Machine-learning-accelerated simulations to enable automatic surface reconstruction. Nat. Comput. Sci. 3, 1034–1044 (2023).
Chanussot, L. et al. Open Catalyst 2020 (OC20) dataset and community challenges. ACS Catal. 11, 6059–6072 (2021).
Tran, R. et al. The Open Catalyst 2022 (OC22) dataset and challenges for oxide electrocatalysts. ACS Catal. 13, 3066–3084 (2023).
Sriram, A.et al. The Open DAC 2023 dataset and challenges for sorbent discovery in direct air capture. arXiv https://doi.org/10.48550/arXiv.2311.00341 (2023).
Pengmei, Z., Liu, J. & Shu, Y. Beyond MD17: the reactive xxMD dataset. Sci. Data 11, 222 (2024).
Deng, B. et al. CHGNet as a pretrained universal neural network potential for charge-informed atomistic modelling. Nat. Mach. Intell. 5, 1031–1041 (2023).
Batatia, I. et al. A foundation model for atomistic materials chemistry. Preprint at https://arxiv.org/abs/2401.00096 (2023).
Brockherde, F. et al. Bypassing the Kohn-Sham equations with machine learning. Nat. Commun. 8, 872 (2017).
Grisafi, A. et al. Transferable machine-learning model of the electron density. ACS Cent. Sci. 5, 57–64 (2018).
Fabrizio, A., Grisafi, A., Meyer, B., Ceriotti, M. & Corminboeuf, C. Electron density learning of non-covalent systems. Chem. Sci. 10, 9424–9432 (2019).
Lewis, A. M., Grisafi, A., Ceriotti, M. & Rossi, M. Learning electron densities in the condensed phase. J. Chem. Theory Comput. 17, 7203–7214 (2021).
Qiao, Z. et al. Informing geometric deep learning with electronic interactions to accelerate quantum chemistry. Proc. Natl. Acad. Sci. USA 119, e2205221119 (2022).
Rackers, J. A., Tecot, L., Geiger, M. & Smidt, T. E. A recipe for cracking the quantum scaling limit with machine learned electron densities. Mach. Learn.: Sci. Technol. 4, 015027 (2023).
del Rio, B. G., Phan, B. & Ramprasad, R. A deep learning framework to emulate density functional theory. Npj Comput. Mater. 9, 158 (2023).
Li, H. et al. Deep-learning density functional theory Hamiltonian for efficient ab initio electronic-structure calculation. Nat. Comput. Sci. 2, 367–377 (2022).
Unke, O. et al. SE (3)-equivariant prediction of molecular wavefunctions and electronic densities. Adv. Neural Inf. Process. Syst. 34, 14434–14447 (2021).
Nigam, J., Willatt, M. J. & Ceriotti, M. Equivariant representations for molecular Hamiltonians and N-center atomic-scale properties. J. Chem. Phys. 156, 14115 (2022).
Zhong, Y., Yang, J., Xiang, H. & Gong, X. Universal machine learning kohn-sham hamiltonian for materials. Chin. Phys. Lett. 41, 077103 (2024).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Condens. Matter Phys. 21, 395502 (2009).
Gong, S. et al. Predicting charge density distribution of materials using a local-environment-based graph convolutional network. Phys. Rev. B 100, 184103 (2019).
Jørgensen, P. B. & Bhowmik, A. DeepDFT: Neural message passing network for accurate charge density prediction. Preprint at https://arxiv.org/abs/2011.03346 (2020).
Jørgensen, P. B. & Bhowmik, A. Equivariant graph neural networks for fast electron density estimation of molecules, liquids, and solids. Npj Comput. Mater. 8, 183 (2022).
Sunshine, E. M., Shuaibi, M., Ulissi, Z. W. & Kitchin, J. R. Chemical properties from graph neural network-predicted electron densities. J. Phys. Chem. C 127, 23459–23466 (2023).
Focassio, B., Domina, M., Patil, U., Fazzio, A. & Sanvito, S. Linear jacobi-legendre expansion of the charge density for machine learning-accelerated electronic structure calculations. Npj Comput. Mater. 9, 87 (2023).
Schütt, K. et al. Schnet: a continuous-filter convolutional neural network for modeling quantum interactions. Adv. Neural Inf. Process. Syst. 30, 991–1001 (2017).
Schütt, K., Unke, O. & Gastegger, M. Equivariant message passing for the prediction of tensorial properties and molecular spectra. In International Conference on Machine Learning, 9377–9388 (PMLR, 2021).
Pope, P. & Jacobs, D. Towards combinatorial generalization for catalysts: a kohn-sham charge-density approach. Adv. Neural Inf. Process. Syst. 36, 60585–60598 (2024).
Shen, J.-X. et al. A representation-independent electronic charge density database for crystalline materials. Sci. Data 9, 661 (2022).
Merchant, A. et al. Scaling deep learning for materials discovery. Nature 624, 80–85 (2023).
Pozdnyakov, S. N. & Ceriotti, M. Incompleteness of graph neural networks for points clouds in three dimensions. Mach. Learn.: Sci. Technol. 3, 045020 (2022).
Thomas, N. et al. Tensor field networks: rotation-and translation-equivariant neural networks for 3d point clouds. Preprint at https://arxiv.org/abs/1802.08219 (2018).
Geiger, M. & Smidt, T. e3nn: Euclidean neural networks. Preprint at https://arxiv.org/abs/2207.09453 (2022).
Ruddigkeit, L., Van Deursen, R., Blum, L. C. & Reymond, J.-L. Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. J. Chem. Inf. Model 52, 2864–2875 (2012).
Ramakrishnan, R., Dral, P. O., Rupp, M. & Von Lilienfeld, O. A. Quantum chemistry structures and properties of 134 kilo molecules. Sci. Data 1, 1–7 (2014).
Jørgensen, P. B. & Bhowmik, A. QM9 Charge Densities And Energies Calculated With VASP. https://doi.org/10.11583/DTU.16794500.v1 (2022).
Jørgensen, P. B. & Bhowmik, A. NMC li-ion Battery Cathode Energies And Charge Densities. https://doi.org/10.11583/DTU.16837721.v1 (2022).
Jain, A.et al. Commentary: The Materials Project: a materials genome approach to accelerating materials innovation. APL Mater.1, 11002 (2013).
Sholl, D. S. & Steckel, J. A. Density Functional Theory (John Wiley & Sons, Ltd, 2009).
Lehtola, S. Assessment of initial guesses for self-consistent field calculations. superposition of atomic potentials: simple yet efficient. J. Chem. Theory Comput. 15, 1593–1604 (2019).
Wing, D. et al. Band gaps of crystalline solids from Wannier-localization–Based optimal tuning of a screened range-separated hybrid functional. Proc. Natl. Acad. Sci. USA 118, e2104556118 (2021).
Passaro, S. & Zitnick, C. L. Reducing SO(3) convolutions to SO(2) for efficient equivariant gnns. In International Conference on Machine Learning, 27420–27438 (PMLR, 2023).
Horton, M. K., Montoya, J. H., Liu, M. & Persson, K. A. High-throughput prediction of the ground-state collinear magnetic order of inorganic materials using Density Functional Theory. Npj Comput. Mater. 5, 1–11 (2019).
Lee, K., Youn, Y. & Han, S. Identification of ground-state spin ordering in antiferromagnetic transition metal oxides using the Ising model and a genetic algorithm. Sci. Technol. Adv. Mater. 18, 246–252 (2017).
Hendrycks, D. & Gimpel, K. Gaussian error linear units (GELUs). Preprint at https://arxiv.org/abs/1606.08415 (2016).
Weiler, M., Geiger, M., Welling, M., Boomsma, W. & Cohen, T. S. 3d steerable cnns: learning rotationally equivariant features in volumetric data. Adv. Neural Inf. Process. Syst. 31, 10381–10392 (2018).
Larsen, A. H. et al. The atomic simulation Environment—a Python library for working with atoms. J. Condens. Matter Phys. 29, 273002 (2017).
Bentley, J. L. Multidimensional binary search trees used for associative searching. Commun. ACM 18, 509–517 (1975).
Virtanen, P. et al. SciPy 1.0: fundamental algorithms for scientific computing in python. Nat. Methods 17, 261–272 (2020).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Int. Conf. Learn. Represent. 3, 1–15 (2015).
Ong, S. P. et al. Python Materials Genomics (pymatgen): a robust, open-source python library for materials analysis. Comput. Mater. Sci. 68, 314–319 (2013).
Hafner, J. Ab-initio simulations of materials using VASP: density-functional theory and beyond. J. Comput. Chem. 29, 2044–2078 (2008).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758–1775 (1999).
Wang, L., Maxisch, T. & Ceder, G. Oxidation energies of transition metal oxides within the GGA+U framework. Phys. Rev. B 73, 195107 (2006).
Jain, A. et al. Formation enthalpies by mixing GGA and GGA+U calculations. Phys. Rev. B 84, 045115 (2011).
Togo, A., Chaput, L., Tadano, T. & Tanaka, I. Implementation strategies in phonopy and phono3py. J. Condens. Matter Phys. 35, 353001 (2023).
Togo, A. First-principles phonon calculations with phonopy and phono3py. J. Phys. Soc. Jpn 92, 012001 (2023).
Acknowledgements
We thank Tess Smidt and Mark Polking for helpful discussions. DISTRIBUTION STATEMENT A. Approved for public release. Distribution is unlimited. This material is based upon work supported by the Under Secretary of Defense for Research and Engineering under Air Force Contract No. FA8702-15-D-0001. Any opinions, findings, conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the Under Secretary of Defense for Research and Engineering. © 2023 Massachusetts Institute of Technology. Delivered to the U.S. Government with Unlimited Rights, as defined in DFARS Part 252.227-7013 or 7014 (Feb 2014). Notwithstanding any copyright notice, U.S. Government rights in this work are defined by DFARS 252.227-7013 or DFARS 252.227-7014 as detailed above. Use of this work other than as specifically authorized by the U.S. Government may violate any copyrights that exist in this work.
Author information
Authors and Affiliations
Contributions
T.K. designed, implemented, and trained the ChargE3Net models. K.Q. collected and prepared the MP, QM9, and NMC datasets, and contributed to the software implementation and training of baseline models. K.Q. devised the angular variation metric and performed analysis on the effects of rotation order together with T.K. E.T. performed experimentation and analysis for initialization of DFT calculations and non-self-consistent calculation of material properties. K.T. provided guidance on DFT calculations. L.L. conceived the project, supervised the research and advised experimentation and data analysis. All authors contributed to the writing and editing of the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Koker, T., Quigley, K., Taw, E. et al. Higher-order equivariant neural networks for charge density prediction in materials. npj Comput Mater 10, 161 (2024). https://doi.org/10.1038/s41524-024-01343-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-024-01343-1
- Springer Nature Limited
This article is cited by
-
Electronic structure prediction of multi-million atom systems through uncertainty quantification enabled transfer learning
npj Computational Materials (2024)