Introduction

The incorporation of nanoparticles (NPs) into polymers is a powerful strategy for improving their thermomechanical properties1,2,3,4 or for introducing new attributes (optical5,6,7,8, electronic9,10,11, magnetic12, or catalytic13,14 properties) into otherwise inert polymers. The surfaces of the NPs are traditionally grafted with polymer ligands to stabilize NP dispersions in the host polymer, as the grafts introduce steric (entropic) repulsion between NPs that, if sufficiently large, can overcome the attractive interparticle forces that promote aggregation15. However, emerging studies show that polymer grafting can also be used to direct NP assembly and access distinctive mesoscopic morphologies such as 1D strings and 2D sheets16,17. These low-dimensional morphologies often exhibit functional properties very distinct from their 3D counterparts (superlattices, globular aggregates)12,18,19,20,21,22. For example, 1D fibrillar and string structures are the basis for colloidal NP gels that exhibit unique rheology, low percolation thresholds, and high porosities23,24,25, enabling the synthesis of functional materials such as hydrogels that exhibit reversible sol–gel transitions and metallic aerogels26 that exhibit high electrocatalytic activity. Noble metal NPs that are assembled into periodic 1D and 2D architectures are known to support collective optical modes as a result of plasmonic coupling19,20, resulting in subwavelength light confinement27, nanoscale waveguiding28, and topological plasmonic edge states29. Polymer grafting has the potential to program assembly in 1D and 2D morphologies as well as control the separation distance and relative orientation (for shaped NPs) between adjacent NPs within the assemblies, both of which are critical for the function of these NP-based assemblies30,31,32.

These highly anisotropic assembly morphologies are a direct manifestation of how polymer-grafted NPs interact with each other but are difficult to predict. Spherical, uniformly grafted NPs exhibit isotropic two-body interactions, which predict the formation of isotropic NP assemblies (unless the two-body potential is deliberately structured, for example, through the introduction of a long-range soft repulsion33,34,35). Thus, the formation of such anisotropic NP phases must arise from higher-body interactions between NPs, that is, perturbative corrections to the free energy from the higher-order arrangement of particles beyond pairwise distances36,37,38. Typically, the interaction free energy \(F\) of an \(N\)-NP system is formulated as a sum over all pairwise interactions between NPs, \(F\cong {\sum }_{i}{\sum }_{j > i}{W}_{2}\left({{\mathbf{\Omega }}}_{i},{{\mathbf{\Omega }}}_{j}\right)\), where \({W}_{2}\left({{\mathbf{\Omega }}}_{i},{{\mathbf{\Omega }}}_{j}\right)\) is the two-body potential of mean force (PMF) between particles \(i\) and \(j\) suitably averaged over all degrees of freedom associated with the grafted and matrix chains, leaving it dependent only on the positions and orientations of the two NPs, which we denote by \({{\mathbf{\Omega }}}_{i}\) and \({{\mathbf{\Omega }}}_{j}\). Thus, the “effective” potential \({W}_{2}\) implicitly accounts for steric repulsion arising from the grafts and depletion-like attraction arising from the matrix, in addition to direct energetic interactions between the cores and grafts of the NPs39,40,41. For spherical NPs grafted uniformly with polymer chains, \({W}_{2}\) is expected to be isotropic and hence a function of interparticle separation distance \({d}_{{ij}}\) only. While such two-body description of interparticle interactions works well for many colloidal systems, higher-body interactions have been shown to become significant for NPs grafted with sufficiently long chains at sufficiently high density37,38,42,43,44,45,46,47,48,49. When two NPs come into contact to form a dimer, their grafts are expelled from the region in between them due to the excluded volume of the NP cores. This leads to an increase in the graft segment density around the contact region of the dimer relative to its poles, causing a third approaching NP to experience additional steric repulsion in that region38. This anisotropic repulsion is indeed what causes the NPs to sometimes form anisotropic structures like 1D strings and 2D sheets in a homogeneous polymer matrix36. Other structural phases like gels have also been observed in NP-polymer systems at high particle loadings50,51,52.

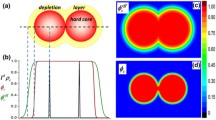
The role of many-body interactions in promoting anisotropic assembly is best illustrated using the simple example of four NPs—the smallest set of particles capable of forming 1D, 2D, and 3D clusters, which may be envisioned as precursors of the string, sheet, and globular assembly morphologies (Fig. 1). The free energy \(F\) of this system, neglecting the single four-body contribution, can be formulated as a sum over six two-body interactions \({W}_{2}\left({d}_{{ij}}\right)\) and 4 three-body interactions \({\triangle W}_{3}\left({d}_{{ij}},{d}_{{ik}},{d}_{{jk}}\right)\), where \({d}_{{ij}}\), \({d}_{{ik}}\), and \({d}_{{jk}}\) are the separation distances between particles \(i\), \(j\), and \(k\). Recent PMF calculations for assembling polymer-grafted NPs show that \({W}_{2}\) exhibits short-ranged attraction with a single minimum, at say \({d}_{{ij}}={d}_{0}\), and \({\triangle W}_{3}\) exhibits short-ranged repulsion that is the strongest when particle triplets form a close-packed triangle and negligible when they arrange into a straight line38. Accordingly, we assume for simplicity that: (1) pairs of NPs gain attractive free energy of \({W}_{2}^{* }\equiv {W}_{2}\left({d}_{0}\right)\, < \,0\) when in direct contact and no energy at larger separations, and (2) triplets of NPs gain repulsive free energy of \(\triangle {W}_{3}^{* }\equiv \triangle {W}_{3}\left({d}_{0},{d}_{0},{d}_{0}\right)\, > \,0\) when they form a close-packed triangular configuration and no energy in all other configurations. The free energies of the idealized 1D, 2D, and 3D clusters of NPs (relative to their dispersed configuration) can be estimated by simply enumerating the number of NP pairs forming direct contacts and number of NP triplets forming close-packed triangles. This analysis finds that the 3D tetrahedral cluster is the most stable structure (with the lowest free energy) when \({\triangle W}_{3}^{* } < {-}{W}_{2}^{* }/2\), the 2D rhombic cluster is the most stable structure when \(-{W}_{2}^{* }/2\, < \,{\triangle W}_{3}^{* } < {-}{W}_{2}^{* },\) and the 1D string cluster structure is the most stable when \({\triangle W}_{3}^{* } > {-}{W}_{2}^{* }\). Even though highly idealized, these calculations provide a compelling illustration of the importance of three-body interactions in stabilizing low-dimensional assembly configurations of polymer-grafted NPs.

Fig. 1: Role of three-body interactions in governing the morphology of clusters formed by polymer-grafted NPs.
figure 1

The left panel shows the fully dispersed and idealized 1D, 2D, and 3D cluster morphologies (string, rhombus, and tetrahedron) formed by four such NPs. The middle and right panels show schematics of the two- and three-body interactions (free energies) between NPs that lead to these distinct morphologies. The free energies \({F}_{1{\rm{D}}}\), \({F}_{2{\rm{D}}},\) and \({F}_{3{\rm{D}}}\) of the three cluster morphologies relative to the dispersed state are also shown. These were calculated by enumerating the number of two-body contacts (blue arrows) and triangular three-body contacts (red triangles) in each cluster that respectively contribute attractive and repulsive energies, the maximum values of which are marked by Asterix. The stability conditions are then \({F}_{3{\rm{D}}}\, < \,{F}_{2{\rm{D}}}\) (or \({\triangle W}_{3}^{* } < {-}{W}_{2}^{* }/2\)) for forming a 3D cluster; \({F}_{2{\rm{D}}}\, < \,{F}_{1{\rm{D}}}\) and \({F}_{2{\rm{D}}}\, < \,{F}_{3{\rm{D}}}\) (\(-{W}_{2}^{* }/2\, < \,{\triangle W}_{3}^{* } < {-}{W}_{2}^{* }\)) for forming a 2D cluster; and \({F}_{1{\rm{D}}}\, < \,{F}_{2{\rm{D}}}\) (\({\triangle W}_{3}^{* } < {-}{W}_{2}^{* }/2\)) for forming a 1D cluster, assuming conditions conducive to assembly (\({W}_{2}^{* }\, < \,0\)).

Full size image

To capture many-body effects in assembly simulations, the NPs, the polymer grafts, and the polymer matrix need to be explicitly modeled. This is computationally expensive, even when using coarse-grained (CG) models, as the system displays many degrees of freedom involving the grafted and matrix polymer chains, and the NPs exhibit highly sluggish dynamics due to their grafts entangling with matrix chains53. Due to this limitation, simulations of large system sizes, long-time scales, and large and complex assemblies are unattainable. A possible solution to this problem is to integrate out the many degrees of freedom of the polymer chains and to model polymer-grafted NPs as individual sites interacting through effective potentials that depend only on interparticle distances. In recent years, machine learning (ML) techniques have been a viable tool to efficiently approximate the many-body interactions in atomistic systems and have been used to speed up ab initio molecular dynamics (MD) simulations54,55,56,57. More recently, ML techniques have also shown great promise for approximating effective interactions in colloidal systems58,59,60,61,62,63. For instance, Campos-Villalobos et al. used an ML approach involving Behler–Parrinello symmetry functions to develop many-body potentials for bare colloidal particles suspended in non-absorbing polymers60. Boattini et al. used a similar approach to model interactions between elastic spheres and explore their assembly in 2D61. A symmetry-function-based approach was also used by Chintha et al. to approximate the two- and three-body interactions between ligand-coated NPs59, though no simulations using the developed potential were conducted to validate it.

Here we introduce a distinct ML approach to develop an analytical many-body potential that can accurately describe the two-body and three-body interactions between spherical polymer-grafted NPs in a polymer matrix. The approach involves the calculation of PMFs of the NPs in the polymer matrix through CG MD simulations and fitting them using permutationally invariant polynomials (PIPs) cast as functions of Coulomb-transformations of interparticle distances55,56. To validate the developed ML potential, we use it to carry out MD simulations of NPs undergoing assembly and show that all known structural phases, namely the 1D strings, 2D sheets, and 3D globular aggregates discussed above, are successfully reproduced. The ML potential reduces the computational cost of MD simulations by at least three orders of magnitude, which allowed us to explore NP assembly at large lengths and time scales and thereby discover additional phases like networks, clusters, and gels that could be assembled from polymer-grafted NPs. Given that the two- and three-body interactions can be easily disentangled in our ML potential, this allowed us to dissect the role of three-body interactions in the formation of each phase.

Results

Description of the many-body potential

An analytical many-body potential is developed here using ML to model the effective interactions between spherical polymer-grafted NPs in a polymer matrix; our overall strategy is summarized in Fig. 2. The potential includes both two-body and three-body interactions according to which the total free energy \({U}_{{\rm{MB}}}\) of the N-particle system is given by

$${U}_{{\rm{MB}}}({{\bf{r}}}^{N})=\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j \,>\, i}{W}_{2}\left({d}_{{ij}}\right)+\mathop{\sum }\limits_{i}\mathop{\sum }\limits_{j \,>\, i}\mathop{\sum }\limits_{k \,> \,j}{\triangle W}_{3}\left({d}_{{ij}},{d}_{{ik}},{d}_{{jk}}\right)$$
(1)

where \({{\bf{r}}}^{N}\) describes the configuration (positions) of the NPs and \({d}_{{ij}}\equiv \left|{{\bf{r}}}_{i}-{{\bf{r}}}_{j}\right|\) the separation distance between NP \(i\) and \(j\). As we later use this free energy surface \({U}_{{\rm{MB}}}\) for computing forces on the NPs to simulate their dynamics, we refer to it as potential energy when discussing it in the context of MD simulations. Higher-body interactions are expected to play a less important role and are not included in this potential to save computational costs. In fact we show later that a three-body description of NP–NP interactions is sufficient to capture all known structural phases exhibited by these NPs.

Fig. 2: Machine learning approach for deriving analytical many-body potentials for modeling the effective interactions between polymer-grafted NPs in a polymer matrix.
figure 2

The approach involves training permutationally invariant polynomials to two- and three-particle PMFs collected from MD simulations. The resulting potential can then be used to investigate the assembly behavior of NPs for orders of magnitude larger length and time scales than achievable through explicit description of the polymer chains.

Full size image

In our many-body potential, the \({W}_{2}\) and \({\triangle W}_{3}\) components are represented using PIPs in Coulombic variables \({y}_{{ij}}\), which are related to interparticle distances \({d}_{{ij}}\) via

$${y}_{{ij}}={\rm {{e}}}^{-k\left({d}_{{ij}}-{x}_{0}\right)}/{d}_{{ij}}$$
(2)

where \(k\) and \({x}_{0}\) are nonlinear parameters that control the width and the position of \({y}_{{ij}}\)55,56. The two-body interaction \({W}_{2}\) between pairs of NPs is expressed as

$${W}_{2}\left({d}_{{ij}}\right)=s({t}_{{ij}})\mathop{\sum }\limits_{n=1}^{M}{C}_{n}{y}_{{ij}}^{n}$$
(3)

where \(s({t}_{{ij}})\) is a switching function that smoothly switches to zero once \({d}_{{ij}}\) exceeds a predetermined cutoff value, \(M\) is the order of the polynomial, and coefficients \({C}_{n}\) are linear fitting parameters. The switching function is given by

$$s\left({t}_{{ij}}\right)=\left\{\begin{array}{l}1\qquad\qquad\qquad{\rm{if}}\,{t}_{{ij}} < 0\\ {\cos }^{2}\left(\frac{{{\pi }}}{2}{t}_{{ij}}\right)\qquad{\rm{if}}\,0\le {t}_{{ij}} < 1\\ 0\qquad\qquad\qquad\,\,{\rm{if}}\,{t}_{{ij}}\ge 1\end{array}\right.$$
(4)

with

$${t}_{{ij}}=\frac{{{d}_{{ij}}-R}_{{\rm{i}}}}{{R}_{{\rm{o}}}-{R}_{{\rm{i}}}}$$
(5)

where \({R}_{{\rm{{i}}}}\) and \({R}_{{\rm{o}}}\) denote the inner and outer radii of the switching function, respectively. The three-body contribution \(\triangle {W}_{3}\) for triplets of NPs is expressed as

$$\triangle {W}_{3}\left({d}_{{ij}},{d}_{{ik}},{d}_{{jk}}\right)=\left[s\left({t}_{{ij}}\right)s\left({t}_{{ik}}\right)+s\left({t}_{{ij}}\right)s\left({t}_{{jk}}\right)+s\left({t}_{{ik}}\right)s\left({t}_{{jk}}\right)\right]\mathop{\sum }\limits_{m=1}^{M}{C}_{{abc}}S\left({y}_{{ij}}^{a}{y}_{{ik}}^{b}{y}_{{jk}}^{c}\right)$$
(6)

where \(S\) is an operator that symmetrizes the monomials \({y}_{{ij}}^{a}{y}_{{ik}}^{b}{y}_{{jk}}^{c}\) (the symmetrized terms are invariant to all permutations among triplets of NPs) and \({C}_{{abc}}\) are linear fitting parameters representing the coefficients of the symmetrized terms with \(a+b+c=m\).

Generation of training data

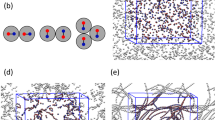
To generate the training data, and later validate the developed potential, we carried out MD simulations of polymer-grafted NPs in a polymer matrix treated using a CG model that captures the most essential physics of NP-polymer systems while keeping the computational costs reasonable38,53,64,65 (Fig. 3a). Briefly, the polymer grafts and the matrix polymer were treated as flexible bead-chains of lengths \({L}_{{\rm{g}}}=10\) and \({L}_{{\rm{m}}}=20\) beads; the beads represent short segments of polymer chains and are all of size \(\sigma\) and mass \(m\). The grafts and matrix polymers are assumed to be fully miscible with each other. Therefore, the graft–matrix, matrix–matrix, and graft–graft intersegment interactions were all treated using a potential that accounts for both excluded volume and attractive interactions, with parameters \(\sigma\) and \(\varepsilon\) specifying the size and attraction strength of the segments. The NP cores were treated as rigid spheres of radius \({R}_{{\rm{NP}}}=\) \(3\sigma\) and mass of \(216m\) that interact with each other using a combined attractive and excluded-volume potential of attraction strength \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\) (unless otherwise stated) and interact neutrally with all polymer segments using an excluded-volume potential. Bare and grafted NPs with grafting densities of \({\Gamma }_{{\rm{g}}}=0.15\) to \(0.4\) chains/\({\sigma }^{2}\) (with the number of grafted chains ranging from 17 to 45) spanning the mushroom to weak-brush grafting regimes were explored. All systems were investigated at a constant temperature of \(T=\varepsilon /{k}_{{\rm{B}}}\) and at a constant polymer segment density of \(0.85\) beads/\({\sigma }^{3}\) producing melt-like conditions for the polymer composite. Based on these grafting densities, graft-matrix miscibility, and relative length of matrix and grafted chains, the polymer-grafted NPs are expected to be in the “wetting regime”, where the matrix chains can penetrate (wet) the polymer grafts. Thus, the primary driver of NP self-assembly is the direct attraction between their cores, which needs to counteract the repulsive steric interactions arising from the grafts. Moreover, these parameter choices have previously38 been shown to produce robust three-body interactions expected to lead to anisotropic structural phases like strings and sheets.

Fig. 3: PMF calculations and PIP fitting results.
figure 3

a Coarse-grained model of the polymer matrix and polymer-grafted NPs at grafting density \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\). The matrix chains are shown in fluorescent green, the grafts in green, and the NP cores in gray. Red dashed line shows the reaction coordinate for calculating the two-body PMF. b Two-body PMF (red circles) and the corresponding PIP potential (blue line) as a function of interparticle distance. Inset shows a zoom of the fit about the minimum. c Schematic of the distance sampling strategy for three-particle PMF calculations. The vertically aligned reaction coordinates along which the force is integrated to compute PMFs are shown by red lines. The three frames indicate nondegenerate sampling of separation distances \({d}_{13}\) and \({d}_{23}\) at three different separation distances \({d}_{12}\) between NP1 and NP2. d, e 3D (top) and 2D (bottom) contour maps of the fitted three-body interactions with respect to interparticle distances \({d}_{13}\) and \({d}_{23}\) (at fixed \({d}_{12}=6.12\sigma\)) (c) and \({d}_{12}\) and \({{d}_{13}=d}_{23}\) (e). The corresponding PMFs computed from simulations are shown in white circles (top; insets show the partial contour map from a bottom view). Representative NP configurations at four corners (purple stars) of the landscape are schematically shown using gray spheres (bottom).

Full size image

The \({W}_{2}\) and \({\triangle W}_{3}\) training data was obtained from PMFs of three polymer-grafted NPs (labeled NP1, NP2, and NP3) in a polymer matrix computed as a function of interparticle distances using the blue moon ensemble method38,66,67. These PMFs were calculated relative to a reference system in which the three NPs are located far from each other where they exhibit no interactions. The \({W}_{2}({d}_{{ij}})\) potential is simply the separation-distance-dependent PMF between a pair of interacting NPs that are isolated from other NPs. To obtain this PMF—\({W}_{2}\left({d}_{12}\right)\) in our case, as we use NP1 and NP2 to compute it—we held the core of NP1 fixed during the simulation while the core of NP2 was brought closer to NP1 in a stepwise manner along a straight-line path passing through its center (red dashed line, Fig. 3a). \({W}_{2}\) was obtained as a function of \({d}_{12}\) by integrating the ensemble-average normal force experienced by NP2 on a finely spaced grid along the path. To ensure that the PMF was not affected by NP3, this NP also was held fixed at a location far from both NP1 and NP2 during the simulation.

The three-body contribution \(\triangle {W}_{3}\left({d}_{{ij}},{d}_{{ik}},{d}_{{jk}}\right)\) is equal to the difference between the overall PMF \({W}_{3}\left({d}_{12},{d}_{13},{d}_{23}\right)\) of our three-NP system and the sum of the two-body PMFs \({W}_{2}\left({d}_{12}\right)\), \({W}_{2}\left({d}_{13}\right)\), and \({W}_{2}\left({d}_{23}\right)\). However, we found that \(\triangle {W}_{3}\) could be more efficiently calculated from a partial three-particle PMF \({W}_{3}^{{\prime} }\) as \(\triangle {W}_{3}={W}_{3}^{{\prime} }\left({d}_{12},{d}_{13},{d}_{23}\right)-{W}_{2}\left({d}_{13}\right)-{W}_{2}\left({d}_{23}\right),\) where \({W}_{3}^{{\prime} }\) includes only interactions of NP3 with NP1 and NP2, and not those between NP1 and NP2. To compute \({W}_{3}^{{\prime} }\), we devised a strategy to sample non-degenerate configurations of the NPs by taking advantage of their indistinguishability and the cylindrical symmetry of the potential (Fig. 3c). This involved placing NP1 and NP2 on the x-axis symmetrically about the origin. For each fixed value of distance \({d}_{12}\) between the two NPs, the position of NP3 was varied across a 2D grid in the first quadrant of the x–y axes, thereby sampling distances \({d}_{13}\) and \({d}_{23}\) of NP3 relative to NP1 and NP2. The ensemble-averaged force on NP3 was computed at each grid point from the simulations and integrating the y-component of this force along gridlines connecting grid points in the y-direction (red lines, Fig. 3c) then yielded \({W}_{3}^{{\prime} }\) as a function of \({d}_{13}\) and \({d}_{23}\) for each fixed \({d}_{12}\).

Fitting of two- and three-body interaction potentials

After computing the effective two-body interaction \({W}_{2}\left({d}_{12}\right)\) and the three-body contribution \(\triangle {W}_{3}\left({d}_{12},{d}_{13},{d}_{23}\right)\) from simulations, the two data sets were individually fitted to the PIP potentials specified in Eqs. (3) and (6). The unknown parameters in the PIPs were obtained through a combination of singular value decomposition and simplex optimization minimizing the mean square error between PIP-predicted and computed potentials using Tikhonov regularization68.

The two-body interactions were computed at 120 distinct values of \({d}_{12}\) in the range \(6\sigma\) and \(14\sigma\), using finer spacings at \({d}_{12}\le 8\sigma\) where it exhibits sharper variations. Figure 3b presents a representative two-body PMF (red circles, Fig. 3b) for polymer-grafted NPs at grafting density \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\). The PMF exhibits a minimum and an energy barrier separating the associated and dissociated states, features that arise from the interplay between short-range attraction between NP cores and a longer-ranged steric repulsion between the NPs due to their grafts. A 7th-order PIP was used for fitting this PMF. This involved the determination of a total of 9 fitting parameters, which includes 7 linear parameters \({C}_{n}\) and 2 nonlinear parameters \(k\) and \({x}_{0}\). The inner and outer radii of the switching function were set to \({R}_{{\rm{i}}}=10\sigma\) and \({R}_{{\rm{o}}}=12\sigma\). The final optimized values of the linear and nonlinear fit parameters are listed in Supplementary Table 1. The RMSD of the full training set is 0.121 \({k}_{{\rm{B}}}T\), and that over the lowest 10 \({k}_{{\rm{B}}}T\) energy range is 0.035 \({k}_{{\rm{B}}}T\). The fitted PIP (blue line, Fig. 3b) shows excellent agreement with the computed PMF (see also parity plot in Supplementary Fig. 1a), capturing well its repulsive shoulder at short distances, its minimum, its energy barrier, and its slow delay over large distances.

The three-body interactions were computed at 4200 combinations of \({d}_{12}\), \({d}_{13}\), and \({d}_{23}\) values, yielding a 3D energy landscape. Supplementary Fig. 2 shows representative 1D energy profiles through this landscape computed for \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\) NPs. The profiles show that the three-body interactions are highly repulsive when an NP approaches a dimer of contacting NPs along the dimer’s perpendicular axis (Supplementary Fig. 2a) and negligible when the NP approaches the dimer along its longitudinal axis (Supplementary Fig. 2b). They also show that the repulsion diminishes as the interparticle distance between the dimer NPs increases (Supplementary Fig. 2c and d). A 5th-order PIP with 15 symmetrized terms involving 17 fitting parameters (15 linear parameters \({C}_{{abc}}\) and 2 nonlinear parameters) was used to fit the three-body interactions. The inner and outer radii of the switching function were set to \({R}_{{\rm{i}}}=6\sigma\) and \({R}_{{\rm{o}}}=10\sigma\). The optimized values of these fit parameters along with the forms of the symmetrized terms are listed in Supplementary Table 2. The RMSD over the full training set is 1.241 \({k}_{{\rm{B}}}T\), and the RMSD over data in the lowest 5 \({k}_{{\rm{B}}}T\) energy range is 0.673 \({k}_{{\rm{B}}}T\) (Supplementary Fig. 1b). Figure 3d presents a contour map of the fitted PIP along \({d}_{13}\) and \({d}_{23}\), for fixed \({d}_{12}=6.12\sigma\), corresponding to the case where a pre-assembled dimer of contacting NPs is approached by a third NP. The fitted PIP shows excellent agreement with the MD-computed PMFs (white circles). Moreover, the fit shows that the three-body contribution is purely repulsive and that the strongest repulsion is observed when the three NPs form a closed triangle (\({d}_{13}\) and \({d}_{23}\) also equal to \(6.12\sigma\)). It also predicts that a third NP would experience the strongest repulsion when approaching the dimer along the perpendicular axis passing through its center and negligible repulsion when approaching along its longitudinal axis. To visualize the three-body interactions and confirm the goodness of the PIP fit in the remaining dimensions, we plotted similar contour maps with respect to distances \({d}_{12}\) and \({d}_{13}={d}_{23}\) (Fig. 3e). We find that the three-body contribution decays rapidly with increasing separation between the dimer NPs.

Validation of optimized many-body potential

To investigate how well the many-body potential developed here reproduced the assembly behavior of NPs treated using the original CG force field with explicit description of polymer grafts and matrix, we again considered polymer-grafted NPs with \({\Gamma }_{{\rm{g}}}\) of \(0.3\) chains/\({\sigma }^{2}\) and carried out MD simulations of three such particles treated using the many-body potential \({U}_{{\rm{MB}}}\) (Eqs. (1)–(6)) with parameters listed in Supplementary Tables 1 and 2. For comparison, we carried out MD simulations of the corresponding system treated using the CG force field as well as MD simulations using only two-body interactions of the many-body potential; we call this a two-body potential and it is denoted by \({U}_{2{\rm{B}}}({{\bf{r}}}^{N})\equiv {\sum }_{i}{\sum }_{j > i}{W}_{2}\left({d}_{{ij}}\right)\). Because the many-body and two-body potential treat the effects of polymer chains implicitly, the entire system of \(N=3\) particles can be described using \(3N=9\) degrees of freedom, whereas the original CG system involved \(N \sim 50,000\) CG beads and thus 150,000 degrees of freedom.

Before analyzing the simulation results, it is instructive to first look at the expected assembly behavior of NPs based on their free energy landscape \({U}_{{\rm{MB}}}\), which has a simple 3D form for a system of three particles, calculated as the sum of three pairwise two-body interactions and a single three-body interaction (see Eq. (1)). This energy landscape is plotted in Fig. 4a with respect to \({d}_{12}\) and \({{d}_{13}=d}_{23}\) and in Supplementary Fig. 3 with respect to \({d}_{13}\) and \({d}_{23}\) (\({d}_{12}\) is fixed at 6.12\(\sigma\)). Both landscape visualizations show that the linear string configuration of NPs exhibits the lowest free energy. Even though a closed-triangle geometry would allow NPs to maximize attractive two-body interactions, this configuration also experiences the strongest three-body repulsion (Fig. 3d and e). Interestingly, the closed triangle appears as a metastable state, where it is surrounded by large energy barriers that separate this configuration from the string or dispersed configurations. These large energy barriers in fact arise mostly from the repulsive three-body interaction (\(\sim \!30{k}_{{\rm{B}}}T\); see Fig. 3d), with a smaller contribution from two-body interactions (\(\sim \!5{k}_{{\rm{B}}}T\); see Fig. 3b). In contrast, an energy landscape composed of pairwise two-body interactions only wrongly predicts the closed triangle as the configuration with the lowest free energy (Fig. 4b). Thus, we expect that proper description of three-body effects in simulations would show the formation of the globally stable linear-string structure with the possibility of also getting trapped in the metastable closed-triangle structure.

Fig. 4: Free energy landscape and assembly dynamics of a three-NP system.
figure 4

a, b 3D (top) and 2D (bottom) contour maps of the many-body potential (a) and the two-body potential (b) with respect to interparticle distance \({d}_{12}\) and \({{d}_{13}=d}_{23}\). Representative NP configurations are schematically shown in the landscape using gray spheres. c, d NP assemblies resulting from two different initial configurations of NPs (top insets): relaxed triangular (\({T}_{0}\)) (c) and string-like (\({S}_{0}\)) (d) arrangement using MD simulations (left; grafting density \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\); bottom insets show NPs without grafts for better visualization), many-body potential \({U}_{{\rm MB}}\) (middle) and two-body potential \({U}_{{\rm 2B}}\) (right). The initial configurations are also roughly marked by the star symbols and the dashed lines indicate the possible assembly pathways (a).

Full size image

We next compared the assembly structures formed by the three NPs in simulations using many-body versus CG potentials. Based on the above discussion on relative stabilities of the linear-string and closed-triangle structures, the NPs were released from two different initial configurations: a relaxed triangle arrangement with \({{d}_{12}=d}_{13}={d}_{23}=7\sigma\) (top insets, Fig. 4c) and a relaxed string arrangement with \({d}_{12}=13.2\sigma\) and \({d}_{13}={d}_{23}=6.6\sigma\) (top insets, Fig. 4d). The initially triangle-arranged NPs in the CG MD simulation ended up dissociating into an NP dimer and an isolated NP after 10 million timesteps (Fig. 4c, left). This behavior is well captured by simulations based on the many-body potential (Fig. 4c, middle). The formation of this configuration originates from the large energy barriers in the energy landscape (Fig. 4a) that prevent the triangularly arranged NPs from forming the closed triangle or the string structure; no such barriers, however, exist to prevent the triangularly arranged NPs from forming a dimer and an isolated NP (star symbols in Fig. 4a indicate initial configuration and dashed lines indicate possible assembly pathways). The initially string-arranged NPs in the CG MD simulations indeed assembled into the linear string (Fig. 4d, left), which again was well captured by our many-body potential (Fig. 4d, middle). As discussed above, the string structure is the globally stable structure with the lowest free energy because three-body repulsion is almost negligible when NPs are arranged in a straight line (Figs. 4a and 3d). Importantly, simulations using the two-body potential falsely predicted the formation of a closed triangle with both initial configurations (Fig. 4c and d, right). In addition, we find that the many-body potential can accurately capture the second peak in the radial distribution function corresponding to string formation, whereas the two-body potential is unable to capture this peak (Supplementary Fig. 4). Thus, the effective many-body potential is not only able to reproduce the structures formed by polymer-grafted NPs but also the underlying assembly pathways.

Large-scale assembly of NPs

So far, we have developed a many-body potential for polymer-grafted NPs of specific grafting density and showed that the potential can correctly capture the tendency of a small system of such NPs to assemble into string-like structures. We next used this potential to study the behavior of much larger systems of NPs, allowing us access to more realistic assembly morphologies formed by such NPs. Meanwhile, we also developed many-body potentials for other NP grafting conditions and used larger systems of those NPs to explore other assembly morphologies.

1D string phase

We started by examining the assembly of 27 NPs of the above string-forming NPs with \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\). As before, we carried out MD simulations using the many-body potential \({U}_{{\rm{MB}}}\), the two-body potential \({U}_{2{\rm{B}}}\), and the explicit CG force field, each initialized from random arrangement of NPs (Fig. 5). The NPs treated using the CG force field eventually assembled into a string phase, but only after ~200 million timesteps corresponding to a time scale of ~\(4\times {10}^{5}{\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) due to the sluggish dynamics of polymer-grafted NPs in polymer melts. The final assembled form of the NPs is shown in Fig. 5a (also see Supplementary Fig. 5). These simulations required ~15,500 CPU hours on AMD EPYC 7742 processors. A similar string-like phase was also obtained in simulations using the many-body potential, but at the computational cost of only ~5 CPU hours on similar processors (Fig. 5b). In contrast, simulations using the two-body potential falsely predicted the formation of NP aggregates (Fig. 5c). For more quantitative comparison, we computed the time-averaged Steinhardt’s bond orientational order parameters69,70 for each NP in the assembled structures. As shown in Fig. 5d, the string-like structures assembled from both the CG force field and the many-body potential exhibit high \({q}_{4}\) and \({q}_{6}\) values that roughly spread over the same region in the \({q}_{4}\)–\({q}_{6}\) plot, confirming that both interaction models produced similar assembly morphologies. In contrast, the order parameters of the NP aggregates predicted by the two-body potential are in the low \({q}_{4}\) and \({q}_{6}\) region and are well separated from those of the string-like phase. Lastly, given the enormous saving in computational cost afforded by our many-body potential, we were able to access NP assembly at even larger length and time scales. Figure 5e presents the assembly outcome of 125 NPs simulated using the many-body potential, revealing the formation of vivid NP strings over much longer time scales of \(4\times {10}^{6}{\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\).

Fig. 5: Large-scale assembly of polymer-grafted NPs at Γg = 0.3 chains/σ2.
figure 5

a Assembly morphology of NPs obtained from MD simulations using CG force field description of polymer chains. Grafts are removed here for better visualization. b Assembly of NPs using the many-body potential \({U}_{{\rm{MB}}}\). Red dashed lines indicate the formation of string-like structures. c Assembly of NPs using the two-body potential \({U}_{2{\rm{B}}}\). d Bond orientational order parameters calculated for each NP in (a–c). Data from simulations using the CG force field, \({U}_{{\rm{MB}}}\), and \({U}_{2{\rm{B}}}\) are marked by green, yellow, and red circles, respectively. e NP assembly at even larger length and time scales using the many-body potential \({U}_{{\rm{MB}}}\).

Full size image

2D sheet phase

Our success with assembling NP strings with the many-body potential prompted us to explore its ability to assemble 2D NP sheets—another structural phase formed by polymer-grafted NPs due to many-body effects. Based on our earlier discussion on cluster morphologies (Fig. 1), 2D clusters are expected to form at intermediate strengths of three-body repulsion—when this repulsion is weak enough to allow the formation of 2D clusters but strong enough to destabilize the formation of 3D clusters. Therefore, we sought to develop a many-body potential for polymer-grafted NPs at a lower grafting density of \(0.15\) chains/\({\sigma }^{2}\) to target the 2D sheet phase. The training data were generated in the same way as described earlier for the densely grafted NPs (Supplementary Fig. 6a). Their fitting procedure using PIPs was also similar, except that a 6th-order PIP was found to be sufficient to fit the two-body PMF. The corresponding fitting parameters are listed in Supplementary Tables 1 and 2, and the parity plots for the two- and three-body contributions are shown in Supplementary Fig. 6b, c.

Figure 6a presents the computed two-body PMF and corresponding PIP fit. The two-body interactions now become stronger and fully attractive because the smaller grafting density reduces the steric repulsion from the grafts. This reduction is also reflected in the three-body interactions (Fig. 6b), which remain repulsive but of weaker strengths (compare to Fig. 3d). The total free energy landscape of three such NPs is presented in Fig. 6c, where the closed triangle is now strongly favored. MD simulations of 27 such NPs (Supplementary Fig. 6d) using the CG model show that NPs indeed assembled into sheet-like structures, which were well captured by our many-body potential (Supplementary Fig. 6e). We also used the many-body potential to simulate the assembly of 125 NPs, which indeed led to the formation of a 2D hexagonal sheet (Fig. 6d). Interestingly, \({W}_{2}^{* }\approx -30{k}_{{\rm{B}}}T\) for contacting pairs of NPs (Fig. 6a) and \({\triangle W}_{3}^{* }\approx 10{k}_{{\rm{B}}}T\) for contacting triangles of NPs (Fig. 6b), so the three-body repulsion is smaller than \(-{W}_{2}^{* }/2\) required to promote the formation of 2D sheets, as per our earlier discussion (Fig. 1). This is because NPs in macroscopic 2D hexagonal sheets possess more triads of NPs compared to the 4-NP sheet, as schematically shown in Supplementary Fig. 7. Since the net repulsion that a NP experiences is given by the sum of the three-body repulsions arising from all triads that the NP forms with neighboring NPs, a smaller strength of repulsion per triad is sufficient to promote the formation of 2D sheets.

Fig. 6: Weakly grafted NPs at Γg = 0.15 chains/σ2 assemble into a 2D sheet phase.
figure 6

a Two-body PMF (red circles) and the corresponding PIP fit (blue line) as a function of interparticle distance. Inset shows a representative configuration of two polymer-grafted NPs captured from our PMF calculations. Red dashed line indicates the reaction coordinate. b, c Contour map of the fitted three-body interaction (b) and the many-body potential (c) with respect to interparticle distances \({d}_{13}\) and \({d}_{23}\) (\({d}_{12}=6.12\sigma\)). Representative NP configurations at specific locations on the landscape are schematically shown by gray spheres. d NPs assemble into 2D sheets when simulated using this many-body potential \({U}_{{\rm{MB}}}\). Inset is a zoomed view of the assembly showing the 2D hexagonal arrangement of NPs.

Full size image

Globular aggregate and dispersed phases

Two other previously reported phases of polymer-grafted NPs are the globular and dispersed phases. To investigate if three-body interactions play a role in the formation of these phases, we considered two additional cases: bare NPs and polymer-grafted NPs at the higher grafting density \({\Gamma }_{{\rm{g}}}=0.4\) chains/\({\sigma }^{2}\), expected to form the globular aggregate and dispersed phases.

Figure 7a presents the two-body PMF of bare NPs in the polymer matrix and the corresponding 5th-order PIPs fit (optimized parameters listed in Supplementary Table 1). As expected, the PMF is fully attractive at distances beyond the excluded zone of NPs (\(d \,> \,2{R}_{{\rm{NP}}}=6\sigma\)). The depth of the PMF at its minimum is roughly equal to the strength of energetic interactions between the NP cores (\({\varepsilon }_{{\rm{NP}}}=30\varepsilon\)). We also computed the three-body interactions between bare NPs and two example profiles are shown in Fig. 7b. The bare NP exhibits almost zero three-body contributions, even when the NP approaches the dimer from its perpendicular axis (\({d}_{12}=6.12\sigma\)) (along which the polymer-grafted NPs exhibited the strongest three-body repulsion; see Figs. 3d and 6b). Thus, only two-body interactions are needed to simulate the assembly of bare NPs, naturally leading to the formation of globular aggregates (Fig. 7c), which was also confirmed by the CG MD simulation of bare NPs in the polymer matrix (Supplementary Fig. 8a).

Fig. 7: Bare and strongly grafted NPs lead to globular aggregate and dispersed phases.
figure 7

a, d Two-body PMFs (red circles) and the corresponding fitting potentials (blue line) for bare NPs (a) and polymer-grafted NPs of grafting density \(0.4\) chains/\({\sigma }^{2}\) (d). Inset shows snapshots of the two kinds of NPs from CG MD simulations. b, e Three-body contributions for these bare NPs (b) and polymer-grafted NPs (e) as a function of the separation distance between a NP and a NP dimer along its perpendicular axis. Contributions for two different dimer configurations (\({d}_{12}\)) are presented. Inset shows corresponding snapshots from MD simulations. c Globular aggregate assembled from NPs using the two-body potential in (a). f Dispersed phase assembled from NPs using two-body potential in (d).

Full size image

Figure 7d shows the two-body PMF of polymer-grafted NPs at \({\Gamma }_{{\rm{g}}}=0.4\) chains/\({\sigma }^{2}\) with the corresponding 6th-order PIPs fit (Supplementary Table 1). At this high grafting density, the steric repulsion from the grafts becomes very strong and outweighs the attraction between NP cores, resulting in purely repulsive two-body interactions that exhibit metastability at a distance corresponding to the minimum of the core-core interaction potential. The three-body repulsion also becomes very strong for these NPs (Fig. 7e). We found that the repulsive two-body interactions were on their own enough to prevent NPs from assembling (Fig. 7f; see also Supplementary Fig. 8c). Since the repulsion keeps NPs well separated, the three-body repulsion experienced by NPs turns out to be very small, as illustrated for the case of an NP approaching a separated NP dimer (\({d}_{12}=10.12\sigma\)) along its perpendicular axis (Fig. 7e). These results demonstrate that even though the three-body interactions are large for densely grafted NPs, they do not play a significant role in NPs forming the dispersed phase as the two-body interactions are even more repulsive.

Lastly, we computed Steinhardt’s bond orientational order parameters for each of the reproduced phases (Supplementary Fig. 8b). We find that the 1D strings, 2D sheets and 3D aggregates assembled from moderately grafted, weakly grafted, and bare NPs can be clearly distinguished through this order parameter with 1D strings exhibiting high \({q}_{4}\) and high \({q}_{6}\) (as strings have strong 2-fold symmetry), the 2D sheets exhibiting relatively low \({q}_{4}\) and intermediate \({q}_{6}\), and 3D aggregates exhibiting low \({q}_{4}\) and low \({q}_{6}\).

Exploratory assembly studies using many-body potentials

Having demonstrated that many-body potentials can reproduce previously discovered structural phases of polymer-grafted NPs in a polymer matrix, we next used the already developed potentials to rapidly explore other assembly scenarios that do not require reparameterization (training). To this end, we considered the many-body potential we developed for polymer-grafted NPs at a grafting density of \(0.15\) chains/\({\sigma }^{2}\) and \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\) that were earlier shown to form 2D sheets (Fig. 6).

We began by exploring the impact of varying the strength of attraction \({\varepsilon }_{{\rm{NP}}}\) between the cores of NPs. Note that this interaction between NP cores does not appear in the three-body interaction, so tuning \({\varepsilon }_{{\rm{NP}}}\) will only affect the pairwise two-body interactions \({W}_{2}\). Even here, changes in \({\varepsilon }_{{\rm{NP}}}\) will simply shift \({W}_{2}(d)\) relative to the one we computed for \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\) by an amount equal to the difference in the new and original attractive core–core potential \({U}_{{\rm{cc}}}\), that is, \({W}_{2}\left({d;}{\varepsilon }_{{\rm{NP}}}\right)={W}_{2}\left({d;}30\varepsilon \right)+{U}_{{\rm{cc}}}\left({d;}{\varepsilon }_{{\rm{NP}}}\right)-{U}_{{\rm{cc}}}\left({d;}30\varepsilon \right)\), which can be rapidly calculated. When we reduced the vdW attraction to \({\varepsilon }_{{\rm{NP}}}=20\varepsilon\), the previously obtained 2D sheets could not be realized, and NPs instead assembled into a loose network of NP strings (Fig. 8a). The reason is that the weaker core-core attraction leads to a weaker two-body attraction between NPs, making the three-body repulsion relatively stronger. This repulsion is now too strong to support the assembly of 2D sheets, but not strong enough to promote assembly of 1D strings, causing the formation of a structure intermediate to the two. On the other hand, increasing the attraction to \({\varepsilon }_{{\rm{NP}}}=40\varepsilon\) led to the formation of small 3D NP clusters that remain stable in size even over a very long timescale of \(4\times {10}^{6}\,{\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) (Fig. 8b). Interestingly, while the stronger two-body attraction should promote continuous merger of clusters until a single globular aggregate remains (Fig. 7c), the three-body repulsion seems to prevent cluster aggregation. This is likely because the many triads of three-body repulsions arising from the NPs in the clusters create energy barriers between each cluster that prevent them from further aggregating.

Fig. 8: Many-body potential facilitates the exploration of assembly morphologies at different NP core attraction strengths and volume fractions.
figure 8

a, b Assembly morphologies obtained at attraction strengths of \({\varepsilon }_{{\rm{NP}}}=20\varepsilon\) (a) and \({\varepsilon }_{{\rm{NP}}}=40\varepsilon\) (b) using many-body potential developed for \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\) NPs that led to 2D sheets. c, d Assembly morphologies obtained at \(\phi =0.22\) using the many-body potentials that led to 2D sheets (c) and 1D strings (d) at \(\phi =0.03\). e Bond orientational order parameters calculated for the assembled structural phases in a–d plotted as the green, red, yellow, and blue points, respectively. The parameters calculated for individual NPs (top) and their average overall from all NPs in each simulation (bottom) are presented.

Full size image

Next, we used this many-body potential (for NPs with \({\Gamma }_{{\rm{g}}}=0.15\) chains/\({\sigma }^{2}\) and \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\)) to study the effect of particle volume fraction \(\phi\), defined as the ratio of the total volume occupied by NPs to the volume of the simulation box. Compared to 2D sheets formed by such NPs at a low \(\phi =\) 0.03 (Fig. 6d), NPs interacting with each other through the same three-body potential assembled into a gel-like phase in simulations at much higher \(\phi =\) 0.22 (Fig. 8c). Although NPs sought to condense due to two-body attraction, the three-body repulsion prevented them from forming a large globular aggregate. Interestingly, their local structure has partial 3D and 2D features (Supplementary Fig. 9a), as confirmed by the bond orientational order parameter of NPs in this phase (Fig. 8e, yellow points), which spread over a region that partially overlaps with those of the 3D aggregate and 2D sheet phases determined earlier (Supplementary Fig. 8b, yellow and red points). We also performed simulations at the same \(\phi =\) 0.22 but using the many-body potential (for NPs with \({\Gamma }_{{\rm{g}}}=0.3\) chains/\({\sigma }^{2}\) and \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\)) that led to the formation of 1D strings (Fig. 5e). As shown in Fig. 8d, these NPs assembled into another gel phase, which at first glance looks like the gel phase described above. However, a closer inspection of its local structure reveals a dense network of short NP strings (Supplementary Fig. 9b) different from the gel phase described earlier. Again, this was confirmed by bond orientational order parameter calculations (Fig. 8e, blue points), which spread over a region of intermediate \({q}_{4}\) and \({q}_{6}\) that overlaps with that of the string network (Fig. 8a and e, green points), indicating a string-like local structure.

Discussion

We developed via ML an analytical potential that can accurately capture many-body interactions between polymer-grafted NPs in a polymer matrix and used the potential to explore NP assembly over large length and time scales. Our approach relies on computing relevant PMFs from CG MD simulations to extract effective two- and three-body interactions between NPs, which are then fitted to permutationally invariant polynomials. As the polymer is explicitly treated in the CG model, these fitted interactions implicitly capture all energetic and entropic effects of the grafted and matrix chains. We validated the many-body potential by comparing the assembly behavior of NPs treated using the fitted potential against those treated using the CG model and demonstrating that the potential can not only accurately reproduce the assembled structures but also capture the assembly pathways. Given that this potential eliminates the need to simulate the numerous degrees of freedom associated with the grafted polymer and the polymer matrix, the potential can speed up NP simulations by at least three orders of magnitude. By simulating the assembly behavior of large systems of NPs over long timescales, we could successfully capture the formation of the experimentally observed 1D string and 2D hexagonal sheet phases and illuminate the critical role of three-body interactions in the formation of these phases. We also elucidated the role of NP interactions on the formation of 3D globular aggregate and dispersed phases and showed that three-body interactions do not play a significant role in their formation. The many-body potentials developed here for specific polymer-grafted NPs also allowed us to rapidly explore assembly behavior under other conditions, e.g., NP core-core interaction strengths and NP volume fractions, without the need for generating new training data. In this manner, we were able to discover several other interesting NP phases, including string networks, small clusters, and two different varieties of gels, where one is a dense network of short 1D strings and the other is a network of partial-2D and 3D motifs. In addition, we showed the utility of Steinhardt’s bond-orientational order parameters in effective classification of NP assemblies.

While our findings support that a three-body potential is enough to reproduce previously discovered phases, higher-body interactions have not been investigated and their role in NP assembly thus remains unclear. However, the fact that we could reproduce all known phases of polymer-grafted NPs using a three-body potential implies the role of higher-body interactions may not be significant. Nonetheless, the accuracy of the developed potential could be further improved by including higher-body interactions. However, this would require computation of high dimensional PMFs, along \(n(n-1)/2\) distinct interparticle distances for each \(n\)-body contribution, which can quickly become prohibitive with increasing \(n\). In such cases, deep neural networks may offer a better alternative for fitting such higher-body contributions.

Our previous work revealed that many-body interactions were responsible for the assembly of quasi-1D structures like serpentine strings and tri-branched networks from polymer-grafted NPs trapped at fluid-fluid interfaces71. However, the full potential of many-body interactions in producing such assembly architectures at interfaces has not been fully explored. The many-body potential developed here could be extended to interfacial environments and coupled with analytical forms of NP-interface interactions72 to uncover anisotropic assembly configurations at fluid interfaces. Although we examined a single species of polymer-grafted spherical NPs so far, it would be worthwhile to apply our ML approach to derive many-body interactions for binary or higher-component NP systems (differing in size and/or polymer grafting), as well as shaped NPs, where many-body effects may be even more prominent. The former application will require reformulation of the PIPs in terms of component-specific interparticle distances and the latter will require additional angular parameters in the PIPs for describing the relative orientation of the NPs, in addition to their separation distance62.

Methods

Coarse-grained model

To compute PMFs between polymer-grafted NPs in a polymer matrix, we adopted a coarse-grained model similar to the one we previously used38. Polymer chains were treated as Kremer–Grest bead-chains73, where beads, each of size \(\sigma\) and mass \(m\), represent short segments of the chain. Chain lengths of \({L}_{{\rm{g}}}=10\) and \({L}_{{\rm{m}}}=20\) beads were used for modeling the grafts and the polymer matrix (Fig. 3a). The NP cores were modeled as rigid spheres of radius \({R}_{{\rm{NP}}}=\) 3\(\sigma\) and mass \({m}_{{\rm{NP}}}=216m\). The grafting points on the surface of the NP cores were uniformly distributed across the surface. We studied both bare NPs (with no grafts) as well as polymer-grafted NP cores of grafting densities in the range \({\Gamma }_{{\rm{g}}}=0.15\)–\(0.4\) chains/\({\sigma }^{2}\).

Adjacent beads of chains signifying bonded segments interact with each other through a combined finitely extensible nonlinear elastic (FENE) spring and Weeks–Chandler–Anderson (WCA) potential74. The FENE spring potential ensures that bonded beads do not stretch beyond a cutoff distance and is given by

$${U}_{{\rm{FENE}}}\left(r{\rm{;}}{k}_{{\rm{s}}},{r}_{0}\right)=-\frac{{k}_{{\rm{s}}}}{2}{r}_{0}^{2}\mathrm{ln}\left[1-{\left(\frac{r}{{r}_{0}}\right)}^{2}\right]$$
(7)

where \(r\) is the separation distance between beads, \({k}_{{\rm{s}}}=30\varepsilon /{\sigma }^{2}\) is the spring constant, \(\varepsilon\) is the characteristic energy parameter, and \({r}_{0}=1.5\sigma\) is the maximum possible spring length. The WCA potential, a short-range purely repulsive potential that models excluded-volume interactions between the bonded segments, can be conveniently cast in the form of a cut-and-shifted Lennard-Jones (LJ) potential:

$${U}_{{\rm{LJ}}}\left(r{\rm{;}}\,\sigma ,\varepsilon ,{r}_{{\rm{c}}}\right)=\left\{\begin{array}{cc}4\varepsilon \left[{\left(\frac{\sigma }{r}\right)}^{12}-{\left(\frac{\sigma }{r}\right)}^{6}-{\left(\frac{\sigma }{{r}_{{\rm{c}}}}\right)}^{12}+{\left(\frac{\sigma }{{r}_{{\rm{c}}}}\right)}^{6}\right] & r\, < \,{r}_{{\rm{c}}}\\ 0 & r\ge {r}_{{\rm{c}}}\end{array}\right.$$
(8)

where the cutoff distance \({r}_{{\rm{c}}}={2}^{1/6}\sigma\). Chains making up the graft and the matrix were considered fully miscible with each other like chains of the same kind. Hence, nonbonded beads within or across any chain interacted with each other via the LJ potential \({U}_{{\rm{LJ}}}\left({r;}\,\sigma ,\varepsilon ,{r}_{{\rm{c}}}=2.5\sigma \right)\), which captures both attractive and excluded-volume interactions due to the larger cutoff of \({r}_{{\rm{c}}}=2.5\sigma\).

The NP cores interact with each other through an expanded LJ potential \({U}_{{\rm{LJ}}}\left(r-2{R}_{{\rm{NP}}};\sigma ,{\varepsilon }_{{\rm{NP}}},{r}_{{\rm{c}}}=2.5\sigma \right)\), where \(r\) is the distance between the centers of the NP cores. The \(2{R}_{{\rm{NP}}}\) shift prevents the NP cores from penetrating each other and \({\varepsilon }_{{\rm{NP}}}=30\varepsilon\) (unless otherwise stated) was used for modeling attractive interactions between the cores. The excluded volume interactions between NP cores and polymer beads were also treated using an expanded WCA potential which can be cast as \({U}_{{\rm{LJ}}}\left(r-{r}_{{\rm{ev}}};\sigma ,\varepsilon ,{r}_{{\rm{c}}}={2}^{1/6}\sigma \right)\), where \(r\) is the distance between the center of the NP core and the polymer bead, and \({r}_{{\rm{ev}}}\equiv {R}_{{\rm{NP}}}-\sigma /2\) is a distance shift that prevents polymer beads from penetrating the NP core.

Molecular dynamics simulations

The LAMMPS package75 was used for carrying out all MD simulations of this NP-polymer system. All simulations were carried out in the canonical (NVT) ensemble at a temperature of \(\varepsilon /{k}_{{\rm{B}}}\) and a polymer density of \(0.85\) beads/\({\sigma }^{3}\). Under these conditions, the polymer matrix exhibits a melt-like state. Periodic boundary conditions were employed in all three directions of the simulation box. A velocity-Verlet algorithm with a time step of \(0.002\) \({\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) and a Nosé–Hoover thermostat of time constant \(1.0\) \({\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) was used for integrating the equations of motion and keeping the system temperature fixed. The simulations were initialized by placing the grafted NPs and the polymer chains in a cubic simulation box 50 times larger than the required dimensions to prevent overlap among the chain beads and NP cores. The box was then gradually shrunk in each direction over a period of 0.8 million timesteps until the targeted polymer density was reached. Simultaneously, the NPs were slowly brought into a configuration used for initiating the PMF calculations or NP assembly simulations. After initialization, we continued the MD simulations for an additional 1 million timesteps to further equilibrate the system while keeping the NPs fixed. During the production period, the net linear and angular momentums of the entire system were zeroed at every step to avoid the “unreal” drifting or rotation induced by the periodic boundary conditions.

Model parameter selection

Our parameter choices were guided by our prior CG simulation study exploring the role of polymer-mediated interactions in the formation of anisotropic structures38, where we obtained a structural phase diagram for a system of three polymer-grafted NPs in a polymer matrix by comparing the formation free energies of linear and triangular trimers for various combinations of graft lengths and grafting densities. Our calculations suggested that NPs with strong grafting conditions (long graft lengths or high grafting densities) would stay dispersed in the matrix, those with moderate grafting (intermediate graft length or density) will form a linear trimer, and those with weak grafting (short grafts and/or low grafting densities) will form a triangular trimer. Furthermore, all three structures could be achieved with a single graft length of \({L}_{{\rm{g}}}=10\) beads and varying the grafting density. Since our CG model is very similar to that used in this prior work, and that these three trimer configurations may be conceived as precursors of the macroscopic dispersed, string, and sheet/globular assembly morphologies, we hypothesized that we should be able to obtain all four morphologies by simply manipulating the grafting density at a fixed graft length of \(10\) beads. Indeed, we find that grafting densities of 0.4, 0.3, 0.15, and 0 chains/\({\sigma }^{2}\) lead to dispersed, string, sheet, and globular phases, respectively.

Potential of mean force calculations

We used the blue moon ensemble method38,66,67 to calculate the two-particle PMF \({W}_{2}\left({d}_{12}\right)\) at grid points along the horizontal path (reaction coordinate) connecting the centers of NP1 and NP2 (see Fig. 3a). Defining the distance between the two NPs along this coordinate as \(\xi\), NP2 was moved towards a fixed NP1 along this coordinate in a stepwise manner starting from a distance \(\xi =14\sigma\) (\(\equiv {\xi }_{0})\), first at steps of Δξ = 0.15σ until a distance of \(\xi =2\sigma\) was reached, then at steps of \(\Delta \xi =0.05\sigma\) until \(\xi =1\sigma\), then at steps of Δξ = 0.02σ until \(\xi =0.2\sigma\), and finally at steps of \(\Delta \xi =0.01\sigma\) until contact. During the mobile phase of each step, the \(\Delta \xi\) change in distance was carried out over 0.05 million timesteps by imposing a small velocity to NP2. During the stationary phase of each step, the center of NP2 was held fixed for 1.2 million timesteps. The ensemble-averaged force \(\langle F(\xi )\rangle\) experienced by NP2 in the direction of NP1 was computed from the last 0.6 million timesteps of this stationary phase. Such forces obtained at the different \(\xi\) values corresponding to the grid points were then integrated to obtain the PMF at any position \({d}_{12}\) along the reaction coordinate:

$${W}_{2}\left({d}_{12}\right)={W}_{2}\left({\xi }_{0}\right)-{\int}_{{\!\xi }_{0}}^{{d}_{12}}\left\langle F\left(\xi \right)\right\rangle {\rm{d}}\xi$$
(9)

where \({W}_{2}\left({\xi }_{0}\right)\) can be approximated as zero, given that \({\xi }_{0}=14\sigma\) is a sufficiently large distance for NP1 and NP2 to interact.

Such force-integration approach was also used for calculating the partial three-particle PMF \({W}_{3}^{{\prime} }\left({d}_{12},{d}_{13},{d}_{23}\right)\) on a 2D grid \(\{{d}_{13},{d}_{23}\}\) representing location of NP3 for each fixed distance \({d}_{12}\) between NP1 and NP2 (see Fig. 3c). We moved NP3 along the vertical gridlines representing reaction coordinates, defining \(\xi\) as the vertical distance of NP3 from the horizonal axis passing through the NP1–NP2 dimer. To traverse each reaction coordinate, we placed NP3 at a distance \({\xi }_{0}=11\sigma\) and moved it in a stepwise manner towards the fixed dimer along the coordinate, first at steps of \(\Delta \xi =0.15\sigma\) until a distance of \(\xi =2\sigma\) was reached, then at steps of \(\Delta \xi =0.05\sigma\) until \(\xi =1\sigma\), then at steps of \(\Delta \xi =0.02\sigma\) until \(\xi =0.2\sigma\), and finally at steps of \(\Delta \xi =0.01\sigma\) until contact. This process is repeated for each of the 12 reaction coordinates (spanning a horizontal distance of \(10\sigma\)) at each of the 6 separation distances \({d}_{12}\) varying from \(6.12\sigma\) to \(10.12\sigma\). The time periods for the mobile and stationary phase and for force averaging were similar to those used for two-body PMF calculations. During each stationary phase, the component of the ensemble-average force experienced by NP3 in the vertical direction was obtained, as denoted by \(\langle F(\xi )\rangle\), and the partial PMF was computed through integration using Eq. 9, where \({\xi }_{0}\) was again chosen to be sufficiently large to prevent any interactions of NP3 with NP1 or NP2.

In both sets of calculations, the three NPs were allowed to rotate throughout the simulations. The simulations along each reaction coordinate were repeated three times to improve accuracy.

Weighted sum of squared residuals

The regularized weighted sum of squared residuals calculated for a given training set is given by55,56

$${{\chi }^{2}=\mathop{\sum }\limits_{n}{w}_{n}[{U}_{{\rm{model}}}(n)-{U}_{{\rm{ref}}}\left(n\right)]}^{2}+{\Gamma }^{2}\mathop{\sum }\limits_{l}{C}_{l}^{2}$$
(11)

Here, \({w}_{n}\) are the weights that emphasize the training data with lower total energy, \({U}_{{\rm{model}}}\) is the permutationally invariant polynomial used for fitting the training set (\({W}_{2}\left(d\right)\) in Eq. (3) for fitting two-body interactions or \(\triangle {W}_{3}\left({d}_{12},{d}_{13},{d}_{23}\right)\) in Eq. (6) for fitting three-body interactions), and \({U}_{{\rm{ref}}}\) is the corresponding reference value in the training set. To avoid overfitting with respect to linear fitting parameters \({C}_{l}\), the regularization parameter \(\Gamma\) was set to \(5\times {10}^{-4}\) for fitting two-body interactions and to \({10}^{-4}\) for fitting three-body interactions. The weights \({w}_{n}\) were assigned as follows:

$$w\left(E\right)={\left(\frac{\triangle E}{E-{E}_{\min }+\triangle E}\right)}^{2}$$
(12)

where \({E}_{\min }\) denotes the lowest energy in the training set and \(\varDelta E\) defines the range of favorably weighted energies, which was set to 10 \({k}_{B}T\) for the fitting of two-body interactions and to 5 \({k}_{B}T\) for the fitting of three-body interactions upon careful experimentation. Both linear and nonlinear parameters were obtained by minimizing the (regularized) weighted sum of squared residuals (Eq. (11)). The linear parameters (\({C}_{l}\)) were obtained through singular value decomposition and nonlinear parameters were optimized using the simplex algorithm55,56.

Simulations using the many-body potential

The three-body potentials were developed through MB-Fit software76 and were then incorporated into LAMMPS75 through MBX software77, where forces and energy of NPs are calculated based on the developed potential. All simulations were carried out in Langevin dynamics at a temperature of \(\varepsilon /{k}_{{\rm{B}}}\), and a damping parameter of \(0.0864{\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) was used so that the dynamics of the NPs matched those of polymer-grafted NPs in the CG MD simulations (Supplementary Fig. 10). Periodic boundary conditions were employed in all three directions of the simulation box. A velocity-Verlet algorithm with a time step of \(0.02{\left(m{\sigma }^{2}/\varepsilon \right)}^{1/2}\) was used for integrating the equations of motion.

Bond orientational order parameters

The averaged Steinhardt’s bond orientational order parameters69,70 were calculated to classify the assembled structural phases. The calculations were performed using the pyscal python module78. A cutoff distance of \(7.5\sigma\) was used to determine the nearest neighbors of a NP. The \({q}_{4}\) and \({q}_{6}\) parameters for each NP or averaged over all NPs were then reported.