Introduction

In recent years, there have been great advances in the use of machine learning to develop interatomic potential models.1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 In this approach, the development of an interatomic potential model is treated as a supervised learning problem,21 in which an optimization algorithm is used to search a hypothesis space of possible functions to find those that best reproduce the energies, forces, and possibly other properties of a set of training data. Potential models developed in this way are often able to achieve accuracy close to that of the method used to generate the training data, with linear scalability and orders of magnitude increase in performance. Alternatively, potential models may be generated by using fundamental physical relationships to derive a simple parameterized function. The parameters of this function are typically then fit to a smaller set of training data. Examples of potential models generated using this latter approach include the embedded-atom method (EAM) and bond-order potentials.22,23,24,25,26,27,28

There are advantages and disadvantages to both approaches to potential model development. Machine learning can be used to develop models for a wide variety of different chemical systems, and because many machine-learning algorithms explore a large hypothesis space, they are often able to achieve very high levels of accuracy on structures where the local environments of the atoms are similar to those that are contained in the data used to train the model.1,2,3 On the other hand, models developed from fundamental physical relationships are often simpler and orders of magnitude faster than machine-learning potential models,29 allowing them to be used to model systems at much longer time and length scales. As they are derived from physics, they can be expected to perform relatively well when they encounter local environments that are unlike the ones they were trained on. The hypothesis space of these potential models is relatively small compared to most machine-learning potentials, meaning that less data is required to train them but also that they are typically unable to achieve the same level of accuracy as many potentials generated using machine learning.

Here, we present a hybrid approach in which machine learning is used to develop simple, fast potential models. Previous work has demonstrated that genetic algorithms can be effectively used to find parameters for interatomic potential models with known functional forms.30,31,32,33,34,35 Our approach adds to these efforts by identifying new functional forms for the models themselves. To accomplish this we use symbolic regression as implemented using genetic programming, in which simple expressions for the potential energy surface are optimized by simulating the process of natural selection.36,37 Genetic programming has been used to rediscover fundamental physical laws38 and applied in materials science to find descriptors of complex material properties.39,40 It has also previously been used to identify simple interatomic potentials.9,41,42,43 Here, we go beyond these previous efforts by demonstrating that genetic programming is capable of finding fast, accurate and transferable many-body potentials for a metallic system from ab-initio calculations.

The key to our approach is the construction of a physically meaningful hypothesis space, achieved by analyzing interatomic potentials that were derived from physical principles.25,27,28 We take advantage of natural similarities in the functional forms of simple, physics-derived models25 to construct a hypothesis space that contains many such functional forms. The hypothesis space that we use consists of all functions that can be constructed from combinations of addition, subtraction, multiplication, division, and power operators; constant values and distances between atoms; and an operator that performs a sum over functions of distances between a given atom and all neighbors within a given cutoff radius. This space contains a wide variety of potential models derived from fundamental physical interactions, including nearly all pair potentials (e.g., Lennard-Jones,44 Coulomb,45 Morse46), as well as many-body glue potentials,25 bond-order potentials (without the bond angle terms),25,26,47,48 and combinations thereof. Even for relatively simple hypothesis spaces such as this one, it is difficult to enumerate a list of even relatively simple functional forms that can be created due to the large number of ways in which the various operators and values can be combined.40 Here, we use a genetic algorithm and multi-objective optimization to search this hypothesis space for interatomic potentials that are simple (and thus more likely to be generalizable49), fast, and accurate. Additional details of our approach are provided in the Methods section.

Results

Validating the machine-learning algorithm

To validate our algorithm, we tested its ability to rediscover the exact form of two interatomic potentials: the Lennard-Jones potential and the Sutton-Chen (SC) EAM potential. In each case, the genetic algorithm was able to identify the exact function used to generate the training data. The training data for the Lennard-Jones potential were generated by taking 75 snapshots (1 snapshot every 5000 steps with a time step of 1 fs) of 32-atom molecular dynamics simulations: 15 snapshots at 80 K in a canonical (NVT) ensemble, 15 snapshots at 80 K and 100 kPa in an isothermal-isobaric (NPT) ensemble, 15 snapshots at 100 K (NVT), 15 snapshots at 100 K and 100 kPa (NPT) and 15 snapshots at 20,000 K (NVT). It consisted of 75 energies and 7200 components of force,50 generated using the following parameterized model for argon:51

$$V_{{\mathrm{LJ}}} = \mathop {\sum }\limits_i \mathop {\sum }\limits_j \left( {\frac{{49304.15}}{{r^{12}}} - \frac{{34.88}}{{r^6}}} \right)$$
(1)

where VLJ is the potential energy of the system, the index i represents an atom in the structure, j is its neighbor and r is the distance between the two atoms. The genetic programming algorithm found:

$$V = \mathop {\sum }\limits_i \left( { - 50.18(983.04)\left( {\mathop {\sum}\limits_j {(3.35r)} ^{ - 6.00} - \mathop {\sum}\limits_j {r^{ - 12.00}} } \right)} \right)$$
(2)

which simplifies to the form of the Lennard-Jones potential in Eq. (1).

The training data for the SC EAM potential were obtained from 100 snapshots (1 snapshot every 100 steps with a time step of 1 fs) of 32-atom molecular dynamics simulations: 25 snapshots at 300 K, 25 snapshots at 1600 K, 25 snapshots at 3800 K, and 25 snapshots at 20,000 K, all in the NVT ensemble. The training set consisted of 100 energies and 9600 components of force. The potential used to generate the training data was parametrized for copper:

$$V_{{\mathrm{SC}}} = \mathop {\sum }\limits_i \left( {\mathop {\sum }\limits_j \frac{{644.52}}{{r^9}} - \left( {\mathop {\sum }\limits_j \frac{{527.62}}{{r^6}}} \right)^{0.5}} \right)$$
(3)

The artificial intelligence algorithm found:

$$V = \mathop {\sum }\limits_i \left( { - 0.73 - 2.53\left( {\left( { - 0.66(384.39)\mathop {\sum}\limits_j {r^{ - 9.00}} } \right) + \left( {0.25/\left( {20.63\mathop {\sum}\limits_j {r^{ - 6.00}} } \right)} \right)^{ - 0.50}} \right)} \right)$$
(4)

When it is simplified, it gives the same form as VSC with a constant shift and a slight difference between the constant parameters that could be eliminated by tightening the convergence criterion for parameter optimization. The values of the parameters in the exponents were found to the second decimal place.

Discovering new models for copper

Having established that our genetic programming algorithm can find the exact form of simple pair and many-body potentials, we evaluated its ability to find potential models from data generated using density functional theory52 (DFT). For this purpose, we generated 150 snapshots (one snapshot every 100 steps with a time step of 1 fs) of 32-atom DFT molecular dynamics simulations on fcc copper: 50 snapshots at 300 K (NVT), 50 snapshots at 1400 K (NVT) and 50 snapshots at 1400 K (NPT at 100 kPa). The copper had melted and lost its fcc structure for the simulations at 1400 K. The data consisted of 150 energies, 14,400 components of forces and 900 components of virial stress tensors.53 One half was randomly selected for training and the other half for validation. Models were evaluated on three metrics: complexity, defined as the number of nodes on the model; computational cost, defined as the number of summations over neighbors, as these typically consume most of the execution time; and fitness, defined as a weighted sum of the mean squared errors of the energies, forces and stresses, which were normalized to unitless values as described in the methods section:

$${\mathrm{Fitness}} = 1000 \ast (0.5{\mathrm{MSE}_{\mathrm{energy}}} + 0.4{\mathrm{MSE}_{\mathrm{force}}} + 0.1{\mathrm{MSE}_{\mathrm{stress}}})$$
(5)

To identify promising models we constructed a three-parameter convex hull based on fitness, computational cost, and complexity. Some of the models on this hull are shown in Table 1.

Table 1 The three-dimensional convex hull of models found by the machine-learning algorithm
Full size table

Many of the models discovered by the genetic programming algorithm have forms that resemble the embedded-atom model, or “glue” type potentials. The models consist of a sum of a pairwise term with a repulsive component and a many-body “glue” type attractive term, which consists of a nonlinear transformation (an “embedding” function) of a sum over neighbors (the “density”). Here, we select two of the models, which we label GP1 and GP2, for further analysis based on their favorable tradeoff between simplicity and their prediction errors for the elastic constants (Supplementary Table S9). In GP1, the simpler of the two models, the embedding function is simply the inverse of the density. In GP2, the embedding function is the same, and it is multiplied by a sum of pairwise interactions to form the glue term. Although GP1 and GP2 resemble known potential models, there are some notable differences. They have much simpler functional forms than most other copper potential models, and they have a different form for the attractive “glue” part of the potential. It is common in EAM-type potential models for the embedding function to be the negative square root of the density; this can be derived from the second moment approximation.25 In GP1 and GP2, the attractive term instead depends on the positive inverse of a sum over pairwise interactions. Unlike the other models, this embedding function is bounded in the limit of high densities and diverges to infinity in the limit of zero density. GP1 and GP2 also include terms with the unusual form of ra−br, which grows by a power law before decaying superexponentially. The resulting models demonstrate high-predictive power for condensed phases and defects that were not included in the training data and, even though there were no surfaces in the data used to train them, they largely avoid the severe underprediction of surface energies that is common for embedded-atom type models (Supplementary Table S6).54

Validating and evaluating the transferability of the interatomic potentials

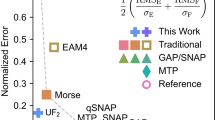
As might be expected by their simplicity, neither GP1 nor GP2 overfit their training data. For each model, there is little difference between the training mean absolute error and validation mean absolute error for energies, components of force vectors and components of the virial stress tensors (Fig. 1). As an initial comparison of the performance between GP1, GP2, and other similar potential models, we evaluate how well they predict the elastic constants of fcc copper. The elastic constants C11, C22, and C44 are a widely used benchmark of copper potential model performance, allowing us to make a comparison between nine different copper potential models for which elastic constant data is available. We have plotted the maximum percent error in predicted elastic constants against the complexity of the model, as measured by number of nodes, in Fig. 2. These errors, and all errors listed in this paper, are measured against each model’s own target values, which are provided in the Supplementary Information. The potentials discovered by the machine-learning algorithm presented in this work significantly change the Pareto frontier of interatomic potentials, defined as the set of interatomic potentials for which no other potential has less error and is less complex. They have errors comparable to the most accurate potential models and complexity comparable to the simplest (Table 2).

Fig. 1
figure 1

Parity plots of training (orange) and validation (blue) energies, components of force and components of the virial stress tensor for the interatomic potential GP1 (first row) and GP2 (second row). The black dashed line is the identity. The mean absolute error (MAE) is presented above each sub-figure for validation and training data, respectively

Full size image
Fig. 2
figure 2

Pareto frontiers of interatomic potentials for copper. No model has less error and is less complex than a model in the Pareto frontier. The orange dashed line was the Pareto frontier before the development of GP1 and GP2, and the blue dashed line is the new Pareto frontier. The percent error for each model was evaluated against the model’s own target values, described in the Supplementary Information. Complexity was measured by the number of nodes in the tree representation of the model. As the smoothing function for some models is unknown, to construct this plot each smoothing function was counted as 2 nodes, representing the smoothing function and a multiplication operation. Sources: SC,79 ABCHM,58 Cu1,58 EAM1,54 EAM2,54 Cu2,80 Cuu6,81 Cuu356 and CuNi.55 The interatomic potentials were found in the Interatomic Potentials Repository.82 GP1 and GP2 were developed in this work

Full size image
Table 2 Interatomic potentials near the Pareto frontiers in Fig. 2
Full size table

Both GP1 and GP2 reproduce the radial distribution function of a liquid state well (Fig. 3), which is likely partially due to the inclusion of snapshots of the liquid state in their training data. There is also good agreement between the newly discovered potential models and other DFT-calculated properties (Table 3). Other models near the Pareto frontiers also show good agreement with their target values, but a notable difference is other than being more complex, these models were also directly trained on many of the properties listed in Table 3 whereas GP1 and GP2 were not. The errors on the elastic constants predicted by GP2 are almost as small as for EAM1, and the simpler model GP1 has errors on elastic constants that are comparable to ABCHM. The GP1 and GP2 models perform well on properties involving hcp and bcc phases, even though no hcp or bcc data were included in the training set. For the bcc lattice constant, the relative energy between the fcc and bcc phases, and the relative energy between fcc and hcp phases, GP1 and GP2 perform comparably to models that were trained on those data points and outperform all models that were not trained on them.

Fig. 3
figure 3

Radial distribution functions of liquid copper at 1400 K

Full size image
Table 3 Error of the values predicted by interatomic potentials for copper relative to the respective reference
Full size table

For vacancy formation energies in the dilute limit, GP2 performs very well, with an error of 2 meV relative to the extrapolated DFT energy (see Supplementary Information for details). GP1 performs less well, with an error of 138 meV. Comparisons with other models for vacancy formation energies are difficult, as the models that report their performance on vacancy formation energies were trained with those values, whereas GP1 and GP2 were not. An exception is a neural network potential we discuss later, for which the extrapolated error is 146 meV, comparable to GP1 (Table S6, Supplementary Information). The GP1 error in vacancy formation energy is largely offset by an error in the opposite direction for migration energy, and as a result the errors for both GP1 and GP2 for the activation energy for vacancy-mediated diffusion are comparable to models that were trained on that value.

GP1 and GP2 also demonstrate good predictive accuracy on phonon frequencies, which were also not included in their training set (Fig. 4 and Table 3). On average, GP2 outperforms all other models on phonon frequencies used for testing, with a mean absolute error of 2.0%, and it also outperforms EAM1 on the phonon frequencies on which EAM1 was trained. GP1 does not do as well as GP2 on phonon frequencies, performing on average slightly better than EAM2 but worse than EAM1 and CuNi. The difference in the performance of GP1 and GP2 on phonons is evident in their calculated phonon dispersion curves (Fig. 4). The strong performance of GP2 on phonon frequencies and elastic constants suggests that it does well at capturing the curvature of local minima on the potential energy surface, but it may not do as well in states away from the local minima, such as the vacancy formation energy of an unrelaxed 2 × 2 × 2 fcc unit cell (Table 3).

Fig. 4
figure 4

Calculated phonon dispersion curves for DFT, GP1, GP2, and GP3

Full size image

Both GP1 and GP2 perform better than the other models for the formation energy of a dumbbell defect. The absolute errors for GP1 and GP2 are only 49 meV and 56 meV, respectively, as compared to an absolute prediction error of 250 meV for the ABCHM model (Table 3). Of the three models that included the dumbbell defect formation energy in their training data, the best has an absolute error that is about twice that of the absolute prediction error of GP2 (Supplementary Table S4). On the other hand, both GP1 and GP2 underestimate the formation energy of a stable intrinsic stacking fault (see Supplementary Information for details) to a greater extent than the other models that report a comparison to this value. The largest absolute error, 29 mJ/m2 for GP1, is 10.2 meV/atom along the (111) plane of the fault. GP1 and GP2 similarly underestimate the formation energy of an unstable stacking fault, but it is hard to assess how this compares to other models as none of the other models reports a benchmark value for the unstable stacking fault energy.

EAM-type models are well known to underpredict surface energies. Surface energies predicted by EAM-type models trained on ab-initio calculations for copper are about 40–50% below their target values for the (100), (110) and (111) surfaces (Supplementay Table S6). In contrast, GP1 underpredicts these surface energies by only 8%, 1%, and 5% respectively, and GP2 underpredicts them by 14%, 10%, and 10%, respectively (Fig. 5). For potentials that use experimental data for their target values, evaluating performance in calculating surface energies is more difficult as only the average value of experimental surface energies is available.54,55,56 To make this comparison we have calculated weighted average surface energies over 13 different low-index surface facets, where the weights are based on the relative surface areas in Wulff constructions (details are provided in the Supplementary Information).57 EAM1 and Cuu3 underpredict the weighted surface energies by about 30%, and CuNi overpredicts the weighted surface energies by about 10% (Supplementary Table S6).58 GP1 underpredicts the weighted surface energies by 8% and GP2 by 13%. GP1-predicted surface energies are the most accurate of any of the evaluated EAM-type potential models relative to its target values.

The performance of GP1 and GP2 on surface energies is remarkable because there were no surfaces in the training set; this is a case of machine-learning potential models demonstrating extrapolative predictive ability. Similarly, both GP1 and GP2 demonstrated high-predictive accuracy for the dumbbell defect compared to the other models, indicating that they are able to accurately predict energies in both low-coordination and high-coordination environments. There are likely two reasons for the predictive accuracy of these models. The first is that other than SC, GP1, and GP2 are the simplest models considered here, and in general simpler models are less likely to overfit the training data.49 A similar trend of simpler models demonstrating greater extrapolative ability was observed by Yunxing et al.19 in a recent comparison of different types of machine learned potential models. The second reason is that these models were discovered in a hypothesis space designed to contain models resembling those for which there is fundamental physical justification. In general, the more physics can be included in the machine-learning procedure, the more likely it is that a model will have extrapolative predictive power.

When new data are added to the training set, the genetic programming search for new models can build off of what has been previously learned by using known high-performing models to seed the search. As a demonstration of this approach, we have performed an additional search using an augmented training set in which the 13 low-index surfaces (shown in Fig. 5) were added to the training data and always included in the subsets of data used to evaluate candidate models. This search was seeded with GP1 and GP2, and as a result the models it discovered (Supplementary Table S10) had many features in common with these. One of these models, which we label GP3 (Eq. (6)) resembles GP2 but, as expected, demonstrates better performance on surface energies (Fig. 5). The absolute error for the weighted surface energies is 7% for GP3, as compared to 13% for GP2. The equation for GP3, which is slightly simpler than that of GP2, is provided below.

$$7.51{\sum} {r^{3.98 - 3.93r}f(r)} + \left( {28.01 - 0.03{\sum} {r^{11.73 - 2.93r}f(r)} } \right)\left( {{\sum} {f(r)} } \right)^{ - 1}$$
(6)
Fig. 5
figure 5

Surface energies of elemental copper as computed using DFT, and the interatomic potentials GP1, GP2, and GP3

Full size image

On average, the improved performance on surface energies for GP3 does not significantly affect its performance on the other properties listed in Table 3 compared to GP2. GP3 performs worse on average on elastic constants and phonon frequencies, but significantly better on the dumbbell formation energy and stacking fault energies. It is difficult to assess the extent to which these changes in performance can be attributed to the addition of surfaces to the training data due to the stochastic nature of the search.

Although GP1, GP2, and GP3 are simpler than many other EAM-type models, they have a similar computational cost when implemented in LAMMPS29,59 due to the extensive use of tabulated values. Based on our benchmarks (Supplementary Fig. S1) GP1 takes 2.1 µs/step/atom, GP2 3.5 µs/step/atom, and GP3 takes 3.6 µs/step/atom, whereas EAM1 has a cost of 3.0 µs/step/atom. These speeds rank them among the fastest potential models, capable of modeling systems at large time and length scales.29

Discussion

There are advantages and disadvantages to the different approaches for using machine learning to generate potential models. In many machine-learning approaches, including (but not limited to) neural network potentials, Gaussian approximation potentials, moment tensor potentials, SNAP potentials, and AGNI force fields,1,2,3,4,5 the general idea is to construct a highly flexible hypothesis space that respects local symmetry and, with the help of large amounts of training data, identify the models within that hypothesis space that best reproduce the training data. Such models are capable of achieving very high-accuracy for systems in which the local environments of the atoms are similar to those contained in the training set. These machine-learning algorithms typically produce potential models that are orders of magnitude faster than DFT but also orders of magnitude slower than EAM-type potentials.29,53,60,61,62

Here, we have demonstrated that machine learning can also be used to develop the types of simple, fast potential models that are needed to model systems at extreme time and length scales. The key to our approach is to use genetic programming to search for computationally simple and efficient models in a hypothesis space that is constructed so that it contains simple models that are also physically meaningful. The models are then selected based on a combination of simplicity, speed, and accuracy relative to the training data. The use of simplicity as a selection criterion results in models that are more likely to generalize well, and it also significantly reduces the amount of data required to train the model.63,64,65 For example, GP1 and GP2 were trained with 75 32-atom structures, for a total of 2400 atomic environments. For comparison, Artrith and Behler66 have constructed a neural network potential for copper with a focus on surfaces. The potential was trained using 554,187 atomic environments, including tens of thousands of slabs and cluster structures. It performs comparably to GP1 and GP2 for many bulk properties, and much better for surface energies (Table S6, Supplementary Information). The neural network approach demonstrates very low errors on the types of systems on which it was trained, but as the genetic programming approach requires less training data it is likely that some accuracy can be recovered by using more accurate (and computationally expensive) methods to generate the training data.

The potential models discovered by the genetic programming approach are as fast as EAM-type models and demonstrate good predictive accuracy on properties they were not trained on. In particular, GP1 and GP2 show surprisingly good performance in predicting surface energies (the GP1 mean absolute error for surface energies is only 35 mJ/m2) despite the fact that there were no surfaces in their training data. Trained only on DFT data, the genetic programming algorithm found models that resemble widely used glue potentials with a unique form for the many-body term that depends on the inverse of a sum over pair interactions. One of the advantages of generating potential models using simple analytical expressions is that it may be possible to analyze the expressions to get an insight into the underlying physical interactions that are responsible for the shape of the potential energy surface.

There are some notable limitations and areas for improvement for the approach presented here. For each system studied, it will be necessary to ensure that the hypothesis space contains simple expressions that capture important contributions to the potential energy; for example, for many systems it will likely be necessary to introduce terms that depend on bond angles, which was not done in this work. We used fixed inner and outer cutoff distances in this study, but it would almost certainly be better to let them vary as do other parameters of the potential. There is also the question of how to determine which of the models discovered by the genetic programming algorithm provide the best balance of speed and predictive accuracy. This could be achieved in a number of ways,40,67,68 including by evaluating performance against validation data, but it is not clear which approach is best. Finally, the genetic programming approach is likely not suitable for on-the-fly learning. As it is a stochastic method, it can take an indeterminate amount of time to find a set of promising models, and there is no guarantee that an incremental change to the training data will result in an incremental change to the shapes of the potential energy surfaces on the convex hull. Other potential model approaches are probably better-suited for this purpose. Despite these current limitations, our results demonstrate that machine learning holds great promise to improve the accuracy of atomistic calculations at extreme time and length scales.

Methods

Description of the hypothesis space

Our machine-learning algorithm uses genetic programming to search a hypothesis space of models that can be constructed by combining real numbers, addition, subtraction, multiplication, division, exponentiation, and a sum over neighbors of an atom. As discussed previously in the text, the hypothesis space was based on physical principles. Within this hypothesis space, each function can be represented as a tree graph, as shown in Fig. 6. The space was constrained so that the maximum number of summations over neighbors was 6, no nested summations over neighbors were allowed, the maximum allowed depth of a tree was 32 and the maximum allowed number of nodes was 511. To ensure smoothness of the potential, all functions of distances are multiplied by the following smoothing function before the sum over neighbors is taken:69

$$f(r) = \left( {2r^2 - 3r_{{\mathrm{in}}}^2 + r_{{\mathrm{out}}}^2} \right)\left( {r_{\mathrm{out}}^2 - r^2} \right)^2\left( {r_{{\mathrm{out}}}^2 - r_{{\mathrm{in}}}^2} \right)^{ - 3}$$
(7)

where rin and rout are the inner and outer cutoff radii, for GP1 and GP2, rin = 3 Å and rout = 5 Å, including the 3rd nearest neighbors.54

Fig. 6
figure 6

Tree graphs of a) a Lennard-Jones potential parametrized for argon, Eq. (1), b) a Sutton-Chen EAM potential parametrized for copper, Eq. (3), c) GP1 and d) GP2

Full size image

Description of the algorithm

Genetic programming evolves computer programs following Darwin’s natural selection by performing crossover and mutation operations on a set of individuals. Crossover was performed by two different operations: by randomly selecting a branch from one tree and replacing it with a randomly selected branch of another tree (Fig. 7), and by creating a linear combination of two randomly selected branches from two different tress—the first method was randomly selected 90% of the time and the second one 10% of the time. The mutation operation performed three different sub-operations with equal probability: crossover of a tree with a randomly generated tree, swapping the arguments of a binary non-commutative function, and slightly modifying the expression tree by replacing (or inserting) a randomly selected non-terminal node with a randomly selected operator.70 The randomly generated trees were generated with the grow or full method with equal probability,36 and the depth was drawn from a Gaussian distribution of mean 5 and standard deviation of 1. The overall algorithm performed crossover with a probability of 0.9, and mutation with a probability of 0.1.

Fig. 7
figure 7

Example of a crossover operation

Full size image

Increasing diversity is known to improve the quality of the optimization.70 To increase diversity, we implemented a hierarchical way of creating separate environments in which the individuals (i.e., potential models) evolved. We ran the algorithm on 12 processors, and each processor had its own environment, consisting of a population of models and a subset of the training data. Conceptually this allows potentials within a specific environment to develop characteristics that are unique, increasing the diversity. Candidates for crossover and mutation were selected from 3 different sets of models with equal probability:

  1. (1)

    The population of the current processor. Every 20,000 crossover and mutation operations, 100 individuals were selected based on their fitness (Eq. (5)) with Pareto tournament selection of size 10 while the rest were discarded.67,71,72

  2. (2)

    A global set of models. Each processor tried to add the 100 individuals selected in part (1) to the global subset every 20,000 crossover and mutation operations. The models on the global set were then evaluated on the basis of speed (to model large time and length scales), fitness (for accurate results), and complexity (for generalizability). The speed of each model was estimated by the number of summations over neighbors. The complexity was evaluated by the number of nodes in the tree graph. To identify the best models, we generated separate convex hulls with respect to fitness and complexity for each number of summations (speed) in a potential. Only the models on these convex hulls were retained in the global set.

  3. (3)

    Individuals from other processors. Each processor was allowed to communicate with other processors every 5000 crossover and mutation operations, importing the current set of individuals from them.

Selection with equal probability was performed when getting an individual from the global set. Tournament selection of size 10 was used for getting individuals from the population of the current processor and from the populations of other processors.

The training data was also arranged in hierarchical subsets to increase diversity and reduce the speed of evaluating fitness. Globally, a subset of 75 energies, 75 forces, and 75 stresses was randomly sampled from the full set of training data every 20,000 crossover and mutation operations. The fitness of the global set of models was evaluated using this subset of training data. The training data on each processor (15–30 energies, forces and stresses) were randomly selected from the global subset of the training data, and this local subset was used to evaluate fitness locally on each processor. The subset of training data for each processor was selected from the global subset because individuals that migrate from a processor to the global set are more likely to survive if the environment is similar.

Optimization of potential model parameters was performed using the covariance matrix adaptation evolution strategy (CMA-ES) optimizer and a conjugate gradient (CG) optimizer.73,74 The CMA-ES algorithm was selected because it performs well in nonlinear or non-convex problems. The potential models on the global set of best individuals were optimized with the CMA-ES every 10,000 crossover and mutation operations by one processor. In contrast, the CG algorithm performed one optimization step for every individual generated by crossover or mutation.

The genetic programming algorithm took about 330 CPU-hours to find the exact Lennard-Jones potential, 3600 CPU-hours to find the exact Sutton-Chen potential, and 360 CPU-hours to find GP1, GP2, and GP3. We note that it is likely that with additional tuning and performance enhancements the efficiency of the algorithm can be improved. To facilitate this, our code is open-source and available at https://gitlab.com/muellergroup/poet.

Details about the target data

The DFT data were computed using the Vienna Ab-initio Simulation Package75 (VASP) with the Perdew–Burke–Ernzerhof76 (PBE) generalized gradient approximation (GGA) exchange correlation functional. The projector augmented wave method77 (PAW) Cu_pv pseudopotential was used for copper. Efficient k-point grids were obtained from the k-point grid server with MINDISTANCE = 50 Å.78 A cutoff energy of 750 eV and ADDGRID = TRUE in VASP were required to converge the stress tensor to less than 0.05 GPa. The elastic constants were converged to within 3 |% error| using a MINDISTANCE = 100 Å. The DFT point defect energies were computed by linear extrapolation (see Supplementary Information for more details). The phonon dispersion curves were computed on a 3 × 3 × 3 supercell. The DFT calculation used a 5 × 5 × 5 k-point grid and electronic self-consistency convergence of 10−8 eV. The radial distribution function molecular dynamics simulations were performed in the NVT ensemble at the experimental 1400 K liquid density on a 3 × 3 × 3 supercell. The temperature was increased from 300 K to 2500 K during 1 ps. Then the temperature was maintained at 2500 K during 10 ps. Then, the temperature was decreased from 2500 K to 1400 K over 1 ps. Then the temperature was maintained at 1400 K during 1 ps. Finally, the radial distribution function data was collected at 1400 K over 40 ps. The DFT molecular dynamics for the radial distribution function was performed with a cutoff energy of 400 eV for the equilibration steps and 750 eV for the final 40 ps during which data was collected. Electronic self-consistency convergence was 10−5 eV and only the k-point at Γ was used. For the computation of the fitness of the models, the energies were transformed by subtracting the minimum and dividing by the standard deviation, and the forces and stresses were standardized by subtracting the mean and dividing by the standard deviation.

The data used to rediscover the Lennard-Jones potential and the SC potential, and the data used to validate GP1 and GP2 were computed with LAMMPS. Instructions and files required to use GP1 and GP2 with LAMMPS are provided on the Supplementary Information. Lennard-Jones calculations used a cutoff distance of 7.5 Å, and SC, GP1, GP2, and GP3 calculations used a cutoff distance of 5 Å.

Benchmarking model speed

Benchmarking of model speed was done on a single core of a Haswell node with a clock speed of 2.5 GHz. The benchmarking simulation consisted of 10,000,000 molecular dynamics steps for a 32-atom unit cell.