Abstract
Inspired by the diverse properties of sulfur hydrides and phosphorus hydrides, we combine first-principles calculations with structure prediction to search for stable structures of Li−P−H ternary compounds at high pressures with the aim of finding novel superconductors. It is found that phosphorus hydrides can be stabilized under pressure via additional doped lithium. Four stable stoichiometries LiPH3, LiPH4, LiPH6, and LiPH7 are uncovered in the pressure range of 100–300 GPa. Notably, we find an atomic LiPH6 with \(Pm\overline 3\) symmetry which is predicted to be a potential high-temperature superconductor with a Tc value of 150–167 K at 200 GPa and the Tc decreases upon compression. All the predicted stable ternary hydrides contain the P–H covalent frameworks with ionic lithium staying beside, but not for \(Pm\overline 3\)-LiPH6. We proposed a possible synthesis route for ternary lithium phosphorus hydrides: LiP + H2 → LiPHn, which could provide helpful and clear guidance to further experimental studies. Our work may provide some advice on further investigations on ternary superconductive hydrides at high pressure.
Similar content being viewed by others
Introduction
Given the metallization and potential room temperature superconductivity of solid hydrogen under high pressure have been proposed,1,2 considerable efforts have been exerted in finding metallic hydrogen. Recently, solid hydrogen metallization has been reported to be realized at 495 GPa,3 but further evidence is needed. Although experimental observations of the metallic hydrogen phase remain controversial, researchers have agreed that hydrogen requires considerable high pressure to reach the metallic state. Doping hydrogen by an impurity has been considered a method for reducing the metallization pressure of pure hydrogen. Ashcroft4 suggested that the metallic hydrogen-rich compounds, such as Group IVa dense hydrides, can be metallic at lower pressures than those necessary for hydrogen given the “pre-compression” provided by non-hydrogen elements. Extensive theoretical investigations have explored that many hydrogen-rich compounds are potential superconductors with rather high superconducting transition temperature (Tc),5,6 such as H3S with Tc of 204 K at 200 GPa,7,8 TeH4 with Tc of 104 K at 170 GPa,9 Si2H6 with Tc of 139 K at 275 GPa,10 CaH6 of 235 K at 150 GPa,11 YH10 of 326 K at 250 GPa,12,13 LaH10 of 286 K at 210 GPa.12,13 Excitingly, hydrogen-rich superconductors H3S14,15 and LaH1016,17 have been successfully confirmed experimentally.
Motivated by the discovery of the high Tc superconductor H3S under high pressure, Eremets et al.18 compressed PH3 and found a Tc of 103 K at 207 GPa. However, the structural information and the origin of the high Tc phase were undetermined. Then, people have exerted efforts on determining this high Tc phase. Theoretical studies showed that all the predicted phosphorus hydrides PHn (n = 1–6) at high pressure were thermodynamically metastable relative to elemental P and solid H2.19,20,21 Among these metastable phases, PH2 possesses the lowest enthalpy with Tc of 76 K21 which responds to the superconducting phase in experimental work.18 Liu et al.20 theoretically searched the structure of PH3 under high pressure and found that the C2/m phase with Tc of 83 K at 200 GPa is in line with the experimental report.20 Experimentally, the PH3 is found to be gradually decomposed into P2H4, P4H6, and then further into elemental phases above 35 GPa at room temperature.22,23 But at lower temperature, P4H6 can be stable up to 207 GPa.23
Although phosphorus is adjacent to sulfur in the periodic table, and the predicted phosphorus hydrides have similar covalent bonds with those in sulfur hydrides, phosphorus hydrides are metastable, whereas sulfur hydrides prefer to form stable H3S under high pressures. Considering that sulfur (3s23p4) has one more valence electron than phosphorus (3s23p3), phosphorus hydrides can be stabilized under pressure by introducing additional electrons. Therefore, we try to dope lithium into the P–H system, and expect to find the stable hydrogen-rich ternary compounds with potential high-temperature superconductivity.
At present, researches on binary hydrogen-rich superconducting compounds have been fruitful and matured, and ternary hydrogen-rich superconducting compounds have gradually been taken seriously. High-pressure experiments found that the ternary hydride BaReH9 is a superconductor with Tc about 7 K at 100 GPa.24 Also in theoretical work, the Tc of Fe2SH3,25 YS4H4,26 and YSH527 at 173, 200, and 300 GPa is about 0.3, 20, and 0.7 K, respectively. Earlier, through theoretical calculations, our group found that after the introduction of Mg in the insulating CH4 system, the Tc of MgCH4 can reach 120 K at 121 GPa.28 Recently, K was also doped into the CH4 system in theoretical work29 and Tc was predicted to be 12.7 K at 80 GPa. In addtion, through adding Li into poor superconductive MgH12, Sun et al.30 found a high-Tc superconductor Li2MgH16 with Tc about 473 K at 250 GPa. What is more, theoretical calculations show that the introduction of alkali metal and alkaline earth metal elements can make the binary Au–H system stable under ambient pressure, and Tc of the Ba(AuH2)2 under ambient pressure is approximate to be 30 K.31
In fact, the precise exploration of the thermodynamic stability of the ternary stoichiometry system is a challenge. For the Li–P–H system, Li and P elements, Li–P, P–H, and Li–H binary boundary compounds are all systematically investigated and exhibit interesting superconducting properties under high pressure.18,19,20,21,22,23,32,33,34,35,36 Li–P compounds are well known as potential solid-state electrolytes in lithium-ion batteries and recently was discovered to be superconductive in Li6P with Tc about 39.3 K under high pressure.36 But LiP stoichiometry gets little attention owing to its poor Li content. At ambient condition, LiP is found to be stable and nonmetal with P21/c symmetry.37,38 Under high pressure,35,36 LiP firstly decomposes into Li3P and P above 13.5 GPa, then it becomes stable again with P4/mmm symmetry above 60 GPa and retains stable till 300 GPa.
Here, we investigated the stabilities and structures of LiPHn (n = 1–7) in the pressure range from 100 to 300 GPa through synthetic route LiP + H2 → LiPHn. Hydrogen-rich compositions, namely, LiPH3, LiPH4, LiPH6, and LiPH7, are found to be stable at high pressure. Above 250 GPa, LiPH6 is thermodynamically stable with \(Pm\overline 3\) symmetry, which is isostructural with ternary hydrides MgSiH6 and MgGeH6.39,40 \(Pm\overline 3\)-LiPH6 is calculated to be a potential high-Tc superconductor with Tc about 150–167 K at 200 GPa and the Tc reduces with pressure increasing.
Results and discussion
We performed the full structure search of the Li–P–H ternary compounds at 100, 200, and 300 GPa by the ab initio evolutionary algorithm as implemented in the USPEX41,42 and constructed the ternary phase diagram in Fig. 1. It is shown that stoichiometries LiPH6 and LiPH7 locate on the convex hull at 100 and 200 GPa. Besides, we found two metastable compounds LiPH3 and LiPH4 which are only 9.9 and 2.0 meV/atom above the convex hull at 200 GPa. At 300 GPa, all ternary compounds become metastable, but LiPH6 and LiPH7 are only 9.1 and 7.0 meV/atom away from the convex hull, respectively. As expected, the LiPHn compounds can be thermodynamically stable under high pressures. For judging the specific synthesis routes for ternary hydrides, our group proposed “triangle straight-line method” (TSLM).31 Through this method, if one ternary compound in the ternary convex hull lies on a straight line connected by any two stable species, then the ternary compound can be synthesized by the two species. In the convex hull of Li–P–H, we found that the stable compounds LiPH6 and LiPH7 lie on the connecting straight line between LiP binary compounds and H2. Herein, the synthetic route LiP + H2 → LiPHn we have chosen for the lithium phosphorus ternary hydrides can be considered feasibly.
The ternary phase diagram of Li, P, and H at a 100, b 200, and c 300 GPa. The corresponding elements and boundary binary phases are chosen from the results of the previous works.32,35,36,43,50,51 The dots represent compositions sampled in our preliminary predictions; dash lines show the synthetic route chosen for further binary convex hulls. Solid and hollow squares represent thermodynamically stable or metastable compositions on the ternary convex hull
Furthermore, we conducted the structure predictions of LiPHn (n = 1–7) with simulation size ranging from two to four for each stoichiometry at the 100, 200, 250, and 300 GPa. The energetic stabilities of LiPHn (n = 1–7) compounds are evaluated by their formation enthalpies compared with LiP and H2, as depicted in Fig. 2a. The stable structures of H2 were taken from the work of Pickard et al.,43 and LiP was taken from the work of Zhao et al.36 As observed, compared with LiP and H2 solids, the stoichiometries of LiPH, LiPH6, and LiPH7 are stable and remain on the convex hull in the pressure range from 100 to 300 GPa; LiPH3 and LiPH4 emerge on the convex hull at 200 and 150 GPa and remain stable until 300 and 250 GPa, correspondingly. To further ensure the stabilities of ternary hydrides, we calculated the formation enthalpies of the above-mentioned LiPHn compounds with respect to two other routes (see Supplementary Fig. 1): Li3P + P + H2 and LiH + P + H2. With respect to Li3P, P, and H2, all the predicted phases are stable in the whole pressure range. With respect to LiH, P, and H2, the LiPH becomes unstable in the whole pressure range. Combining the data given in the convex hull (Fig. 2a), the final phase diagram of LiPHn is demonstrated in Fig. 2b. The LiPH3 is stable with P2/m structure from 200 to 300 GPa, and LiPH4 is stable with P21/m structure from 150 to 250 GPa. LiPH6 is stable with C2/c structure from 100 to 250 GPa and then convert into the cubic \(Pm\overline 3\) structure. LiPH7 started to be stable from 100 GPa with \(P\overline 1\) structure and transformed to C2/m structure at 250 GPa.
Zero-point energy (ZPE) has been important in the total energy of hydrogen-rich compounds. Therefore, we used the quasi-harmonic model to estimate the ZPE of LiPHn (n = 1–7) compounds under 300 GPa (see Supplementary Fig. 2). After considering the ZPE, the formation enthalpies of the predicted phases at 300 GPa are not various obviously and the overall stability does not change. Thus, the ZPE does not considerably influence the total stability of the phase diagram. The phonon band structures of all thermodynamically stable phases are exhibited in Supplementary Fig. 3. The lack of imaginary phonon frequency indicates that they are all dynamically stable.
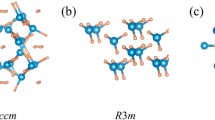
A survey of the distinctive features of the predicted structures is displayed in Fig. 3, and the structure parameters are listed in Supplementary Table 1. For P2/m-LiPH3 at 200 GPa, the P atoms formed distorted cubic units with the P–P bonds at approximately 2.10 Å. In the electron localization function (ELF) presented in Supplementary Fig. 4, electrons accumulate between P atoms, thereby indicating the P–P covalent bonds. The distorted cubic connected each other into a sheet with hydrogen saturating the dangling bonds. In the P–H sheets, every distorted cubic unit contains a monoatomic H at the center. Symmetrical with the P–H sheet, two other kinds of sheets are stacked along the b-axis: one consists of Li atoms; another consists of H2 units with 0.88 Å bond lengths and monoatomic hydrogen atoms. For P21/m-LiPH4 at 150 GPa, high electron densities are found between P–P and P–H in the ELF. Therefore, P atoms connect as zigzag chains with P–P bonds at approximately 2.10 Å. Every P atom connects four H atoms with P–H bonds ranging from 1.40 to 1.44 Å. Li atoms arrange along the P–H chains. When hydrogen content increases, as indicated in the ELF, P atoms absorb additional hydrogen atoms and form PHn units. In C2/c-LiPH6 and \(P\overline 1\)-LiPH7 at 250 and 150 GPa, the PH6 units are found as distorted octahedrons with P–H bonds at approximately 1.35–1.36 and 1.37–1.40 Å, correspondingly. In the high-pressure range, C2/m-LiPH7 possesses PH11 units with P–H bonds at approximately 1.50–1.58 Å at 300 GPa. Every PH11 unit is connected by H–H bonds with 0.96 and 1.07 Å. At above 250 GPa, the C2/c phase of LiPH6 transforms into an A15-like structure with \(Pm\overline 3\) symmetry, that is, isostructural with MgSiH6 and MgGeH6 predicted by our group.31,40 In \(Pm\overline 3\)-LiPH6, the H–H distances are 1.14 Å at 300 GPa and low electron densities between all the atoms in the ELF indicate the atomic character of this phase.
In previous theoretical works on the metastable P–H system, most PHn (n = 1–3) structures consist of P–P layers or P–P chains with H atoms hanging on the P frameworks by P–H bonds.19,20,21 The dimensionality of the P frameworks decreases from layers (PH, PH2) to chains (PH3, PH4). Then, in PH5 and PH6, the P–H polymers exist and connected by H–H bonds.19 In LiPHn (n = 1–7), except for the atomic phase \(Pm\overline 3\)-LiPH6, the P–H and P–P sublattices in LiPHn (n = 1–7) structures are similar to those in the PHn structures, that is, the layers of PH in LiPH3, the chains of PH4 in LiPH4, and the polymers of PH6 and PH11 in LiPH6 and LiPH7. Thus, lithium does not change the connect manner of phosphorus and hydrogen but stabilize the phosphorus hydrides under high pressure.
Before calculating the superconductive properties of LiPHn compounds, we explored their electronic structures. In the calculated band structures with projection (Fig. 4), except for the low-pressure phases C2/m-LiPH6 and \(P\overline 1\)-LiPH7, all the other stable phases are metallic. The bands near the Fermi level are mainly provided by H and P and rarely come from Li. The Bader charge analysis44 (see Supplementary Table 6) shows that Li and P atoms play roles as electron donors and provide electrons to H atoms. For all the stable phases, Li constantly loses approximately 0.8e. This phenomenon indicates that, for every metastable PHn, nearly one electron is required for their stabilization, and this requirement is satisfied by lithium. However, the electrons that P loses and the electrons that H gains are different from each stable phase. For non-metallic phase C2/c-LiPH6 and \(P\overline 1\)-LiPH7, and poor metallic phase P21/m-LiPH4, every P atom loses approximately 2.88, 2.76, and 1.43e, and every H atom receives nearly 0.61, 0.51, and 0.56e, respectively. For other metallic phases P2/m-LiPH3, \(Pm\overline 3\)-LiPH6, and C2/m-LiPH7, every P atom loses 0.23, 1.28, and 1.23e and every H atom receives 0.33, 0.34, and 0.29e, correspondingly. In metallic phases, fewer electrons around H atoms than those in non-metallic and poor metallic phases are present, thereby indicating more free electrons in metallic phases. With the increase in the H contents in metallic phases, the H-derived electronic DOS gradually dominates at the Fermi level NF (Fig. 5). For P2/m-LiPH3, the values P-derived electronic DOS contribute most to the NF. For \(Pm\overline 3\)-LiPH6 and C2/m-LiPH7, the values of NF are mainly contributed by electrons projected to the H atoms. Therefore, the hydrogen-rich LiPHn compounds may produce promising superconductivities.
Electron band structures of a P2/m-LiPH3 at 200 GPa, b P21/m-LiPH4 at 150 GPa, c C2/c-LiPH6 at 250 GPa, d \(Pm\overline 3\)-LiPH6 at 300 GPa, e \(P\overline 1\)-LiPH7 at 150 GPa, and f C2/m-LiPH7 at 300 GPa. The Fermi level is set to zero and depicted as the red dash line. The red, blue, and green dots represent the contributions of H, P, and Li atoms to the electron bands
Electron density of states of a P2/m-LiPH3 at 200 GPa, b P21/m-LiPH4 at 150 GPa, c \(Pm\overline 3\)-LiPH6 at 300 GPa, and d C2/m-LiPH7 at 300 GPa. The Fermi level is set to zero and depicted as the red dash line. The black solid line represents the total density of states. The pink, purple, and green solid line represent the electron density of states projected onto H, P, and Li atoms, respectively
We investigated the superconductivities of the metallic LiPHn compounds at different pressures by calculating the EPC parameter λ, the logarithmic average phonon frequency ωlog, and the superconductive critical temperature Tc (Table 1). For poor metallic phase P21/m-LiPH4 at 150 GPa, the λ is 0.25, and ωlog is 1222.8 K. The small values of λ and ωlog cause the low Tc at approximately 0.05 K, which is close to 0. For P2/m-LiPH3 and C2/m-LiPH7, the EPC parameters of λ are 0.82 and 0.74, and the calculated ωlog values are 1131.5 and 1434.0 K at 200 and 300 GPa, respectively. Using the corrected Allen–Dynes-modified McMillan equation, their Tc values are 48.8–60.4 and 46.0–59.2 K with the Coulomb pseudopotential μ* = 0.1–0.13, correspondingly.
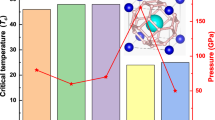
Although atomic phase \(Pm\overline 3\)-LiPH6 starts to be stable above 250 GPa, we found that it can be dynamically stable when decompressed to 200 GPa, and we calculated the superconducting critical temperature Tc of \(Pm\overline 3\)-LiPH6 as a function of pressure (Table 1). At 200, 250, and 300 GPa, the calculated values of Tc are 167.3, 148.3, and 128.6 K, respectively. The Eliashberg phonon spectral function α2F(ω) and projected phonon density of states (PHDOS) of \(Pm\overline 3\)-LiPH6 at different pressures are illustrated in Fig. 6. Under the pressures of 200, 250, and 300 GPa, the contributions of Li, P, and H atoms to the total λ and total ωlog are shown in Fig. 6. The P atoms dominate the low-frequency regions (0–500 cm−1) which contribute about 23.0–31.7% to the total λ and 5.7–8.6% to the total ωlog. For the case of Li atoms, they dominate the middle-frequency regions (500–1000 cm−1), contribute about 13.0–17.8% to the total λ, and 3.8–3.9% to the total ωlog. While the H atoms which dominate the high-frequency regions (>1000 cm−1) contribute about 55.3–59.2% to the total λ and 87.5–90.4% to the total ωlog. Hydorgen plays a dominating role in electron–phonon coupling and logarithmic average phonon frequency. Therefore, the high Tc of \(Pm\overline 3\)-LiPH6 mainly comes from H atoms.
The phonon band structure (left), PHDOS, and Eliashberg spectral function α2F(ω) (right) for \(Pm\overline 3\)-LiPH6 at different pressures. Red solid circles indicate the phonon line width with a radius proportional to the EPC strength. The integral λ and ωlog as a function of frequency are calculated and shown in red and blue solid lines. The contributions of the P, Li, and H atoms are illustrated in percentages
With the increase in pressure, the Tc decreases from 167.7 to 128.6 K. At the same time, the ωlog increases from 1119.2 to 1429.4 K whereas λ decreases from 1.62 to 1.11. Therefore, the change of Tc is dominated by λ under pressure. We further studied the change of the partial ωlog and λ of Li, P, and H atoms under pressure (Table 2). From 200 to 300 GPa, the ωlog-P reduces from 96.1 to 81.4 K while the ωlog-Li increases from 43.8 to 55.6 K. As a result, the total value of low- and middle-frequency ωlog-LiP are almost unchanged under pressure. The increase of ωlog is mainly due to the increase of ωlog-H (from 979.3 to 1292.4 K). With the increase of pressure, the partial constants of EPC λH and λP reduce a lot from 0.895 to 0.675 and 0.515 to 0.256, respectively, while the λLi varies little from 0.210 to 0.197. Thus, the decrease of λ is mainly dominated by the reduction of λH and λP, which is due to the large contribution of H and P atoms to the Fermi level NF.
The predicted metastable superconductor PH3 possesses Tc at approximately 83 K with estimated λ and ωlog at nearly 1.45 and 826 K for 200 GPa.20 At the same pressure, \(Pm\overline 3\)-LiPH6 has a Tc at approximately 149.6–167.3 K with λ and ωlog at nearly 1.62 and 1119.2 K, respectively. The λ and ωlog values of \(Pm\overline 3\)-LiPH6 are larger than those of PH3, thus causing a larger Tc. The doping of Li atom makes the total mass of LiPH6 lighter than that of PH3, which can produce a large Debye temperature. Moreover, three clear phonon frequency regions that correspond to P, Li, and H can be found in \(Pm\overline 3\)-LiPH6 and the atomic H has a wide and continuous high-vibration frequency region (1000–2500 cm−1) and contributes considerably to the EPC. In the case of PH3, strong hybridization of P and H makes the low- and middle-frequency regions contribute most to the total EPC, thereby possibly causing a low λ value.
To further explore the superconductivities and provide some information to experiment, the McMillan isotopic coefficient β and critical magnetic fields μ0Hc(0) of LiPHn (n = 3, 6, and 7) and critical temperature Tc of LiPDn (n = 3, 6, and 7) are estimated in Table 1. Because the Tc of LiPH4 is near zero, we did not calculate its β, μ0Hc(0), and Tc of LiPD4. It is clear that the isotopic coefficient β values always maintain about 0.5. For P2/m-LiPH3 and C2/m-LiPH7, the critical magnetic fields μ0Hc(0) are estimated to be about 6.8–8.5 and 6.4–8.4 T at 200 and 300 GPa, respectively. For the high-Tc superconductor \(Pm\overline 3\)-LiPH6, the estimated μ0Hc(0) value is as high as 28.7–32.9 T at 200 GPa, and gradually decreases to 16.1–19.0 T at 300 GPa.
In summary, we have explored the crystal structures and stabilities of Li−P−H ternary system under high pressure by employing the evolutionary algorithm USPEX in combination with first-principles calculations. It is found that Li can stabilize metastable P–H compounds and form stable ternary hydrides LiPH3, LiPH4, LiPH6, and LiPH7 under high pressure. Except for the low-pressure phases of C2/c-LiPH6 and \(P\overline 1\)-LiPH7, all the other stable LiPHn phases are metallic. Among the metallic phases, P2/m-LiPH3 and C2/m-LiPH7 are superconductive with Tc of 49–60 and 46–59 K at 200 and 300 GPa, respectively. Their critical magnetic fields are about 6–8 T. Significantly, atomic phase \(Pm\overline 3\)-LiPH6 has a high Tc and high μ0Hc(0) values about 149–167 K and 28.7–32.9 T at 200 GPa, respectively. As pressure increases to 300 GPa, the Tc and μ0Hc(0) decrease to 110–128 K and 16.1–19.0 T, correspondingly. The high Tc value of \(Pm\overline 3\)-LiPH6 under pressure is closely related to the large H-derived electronic DOSs at the Fermi level, strong EPC and high logarithmic average frequency associated with vibrations of atomic H, and the light masses of Li atoms. The exploration of ternary phase diagrams is a challenging task, but the study of ternary hydrides remains valuable. Ternary hydrides frequently achieve some goals that are unachievable in binary hydrides by introducing a third type of element, such as stabilizing the metastable binary hydrides, metalizing the insulative binary hydrides with strong covalent bonds, further reducing the superconducting pressures of some high Tc binary hydrides. Furthermore, ternary hydrides may produce some other new high Tc phases, such as the atomic phase of \(Pm\overline 3\)-LiPH6.
Methods
Variable composition searches of the Li–P–H ternary phase at 100, 200, and 300 GPa were conducted through the evolutionary algorithm USPEX41,42 code with respect to element Li, P, and H. One hundred and twenty structures were created using a random symmetric generator in the first generation, all subsequent generations contained 85 structures and were produced using variation operators such as heredity (50%), softmutation (20%), transmutation (10%), 20% of each new generation was produced randomly. Then, we explored the stable compounds of LiPHn (n = 1–7) based on the fixed composition search implemented by USPEX41,42 with respect to the binary compounds LiP and H2. It was performed at 100, 200, 250, and 300 GPa using original cells ranging from two to four formula units. All the structural relaxations, electronic properties, and total energy calculations are conducted using the VASP package45 in the framework of DFT with Perdew–Burke–Ernzerhof parameterization of the generalized gradient approximation.46 The projector-augmented wave approach47 was adopted to describe ion–electron interactions, where 1s1, 1s22s1, and 3s23p3 are considered as valence electrons for H, Li, and P atoms, respectively. A plane-wave energy cutoff of 800 eV was used. We applied a Brillouin zone sampling grid spacing of 2π × 0.03Å−1 for structure relaxations and 2π × 0.02Å−1 for electronic property calculations. Lattice dynamics and electron–phonon coupling (EPC) were characterized by density functional perturbation theory as implemented in the Quantum-ESPRESSO package.48 Norm-conserving potentials for H (1s1), Li (1s22s1), and P (3s23p3) were used with a kinetic energy cutoff of 80 Ry. The k- and q-points meshes in the first BZ are 24 × 12 × 24 and 4 × 2 × 4 for P2/m-LiPH3, 20 × 20 × 12 and 5 × 5 × 3 for P21/m-LiPH4, 24 × 24 × 24 and 6 × 6 × 6 for \(Pm\overline 3\)-LiPH6, and 20 × 20 × 12 and 5 × 5 × 3 for C2/c-LiPH7. Their superconductive transition temperatures Tc are estimated through the Allen−Dynes-modified McMillan equation with correction factors.49 The calculation details of superconductive properties can be seen in Supplementary Information.
Data Availability
The datasets used in this article are available from the corresponding author upon request.
References
Ashcroft, N. W. Metallic hydrogen: a high-temperature superconductor? Phys. Rev. Lett. 21, 1748–1749 (1968).
Wigner, E. & Huntington, H. B. On the possibility of a metallic modification of hydrogen. J. Chem. Phys. 3, 764–770 (1935).
Dias, R. P. & Silvera, I. F. Observation of the Wigner-Huntington transition to metallic hydrogen. Science 355, 715 (2017).
Ashcroft, N. W. Hydrogen dominant metallic alloys: high temperature superconductors? Phys. Rev. Lett. 92, 187002 (2004).
Duan, D. et al. Ab initio approach and its impact on superconductivity. J. Supercond. Nov. Magn. 32, 53–60 (2019).
Duan, D. et al. Structure and superconductivity of hydrides at high pressures. Nat. Sci. Rev. 4, 121 (2017).
Duan, D. et al. Pressure-induced decomposition of solid hydrogen sulfide. Phys. Rev. B 91, 180502 (2015). (R).
Duan, D. et al. Pressure-induced metallization of dense (H2S)2H2 with high-Tc superconductivity. Sci. Rep. 4, 6968 (2014).
Zhong, X. et al. Tellurium hydrides at high pressures: high-temperature superconductors. Phys. Rev. Lett. 116, 057002 (2016).
Jin, X. et al. Superconducting high-pressure phases of disilane. Proc. Natl. Acad. Sci. USA 107, 9969–9973 (2010).
Wang, H. et al. Superconductive sodalite-like clathrate calcium hydride at high pressures. Proc. Natl. Acad. Sci. USA 109, 6463–6466 (2012).
Liu, H. Y. et al. Potential high-Tc superconducting lanthanum and yttrium hydrides at high pressure. Proc. Natl. Acad. Sci. USA 114, 6990–6995 (2017).
Peng, F. et al. Hydrogen clathrate structures in rare earth hydrides at high pressures: possible route to room-temperature superconductivity. Phys. Rev. Lett. 119, 107001 (2017).
Drozdov, A. P. et al. Conventional superconductivity at 203 kelvin at high pressures in the sulfur hydride system. Nature 525, 73–76 (2015).
Einaga, M. et al. Crystal structure of the superconducting phase of sulfur hydride. Nat. Phys. 12, 835–838 (2016).
Somayazulu, M. et al. Evidence for superconductivity above 260 K in Lanthanum superhydride at megabar pressures. Phys. Rev. Lett. 122, 027001 (2019).
Drozdov, A. P. et al. Superconductivity at 250 K in lanthanum hydride under high pressures. Nature 569, 528–531 (2019).
Drozdov, A. P., Eremets, M. I. & Troyan, I. A. Superconductivity above 100 K in PH3 at high pressures. arXiv 1508, 06224 (2015).
Flores-Livas, J. A. et al. Superconductivity in metastable phases of phosphorus-hydride compounds under high pressure. Phys. Rev. B 93, 020508 (2016).
Liu, H. et al. Crystal structure and superconductivity of PH3 at high pressures. J. Phys. Chem. C 120, 3458–3461 (2016).
Shamp, A. et al. Decomposition products of phosphine under pressure: PH2 stable and superconducting? J. Am. Chem. Soc. 138, 1884–1892 (2016).
Liu, M. et al. Unravelling decomposition products of phosphine under high pressure. J. Raman Spectrosc. 49, 721–727 (2018).
Yuan, Y. et al. Stoichiometric evolutions of PH3 under high pressure: implication for high Tc superconducting hydrides. Nat. Sci. Rev. https://doi.org/10.1093/nsr/nwz010 (2019).
Muramatsu, T. et al. Metallization and superconductivity in the hydrogen-rich ionic salt BaReH9. J. Phys. Chem. C 119, 18007–18013 (2015).
Zhang, S. et al. Structure and electronic properties of Fe2SH3 compound under high pressure. Inorg. Chem. 55, 11434–11439 (2016).
Grishakov, K. S., Degtyarenko, N. N. & Mazur, E. A. Electron, phonon, and superconducting properties of yttrium and sulfur hydrides under high pressures. J. Exp. Theor. Phys. 128, 105–114 (2019).
Chen, J. et al. Computational design of novel hydrogen-rich YS–H compounds. ACS Omega 4, 14317–14323 (2019).
Tian, F. et al. Predicted structures and superconductivity of hypothetical Mg-CH4 compounds under high pressures. Mater. Res. Express 2, 046001 (2015).
Han, J.-X., Zhang, H. & Zhong, G.-H. Metallization and superconductivity in potassium-doped methane. Int. J. Mod. Phys. C 30, 1950061 (2019).
Sun, Y. et al. Route to a superconducting phase above room temperature in electron-doped hydride compounds under high pressure. Phys. Rev. Lett. 123, 097001 (2019).
Rahm, M., Hoffmann, R. & Ashcroft, N. W. Ternary gold hydrides: routes to stable and potentially superconducting compounds. J. Am. Chem. Soc. 139, 8740–8751 (2017).
Zurek, E. et al. A little bit of lithium does a lot for hydrogen. Proc. Natl. Acad. Sci. USA 106, 17640–17643 (2009).
Howie, R. T. et al. High-pressure synthesis of lithium hydride. Phys. Rev. B 86, 064108 (2012).
Pépin, C. et al. Synthesis of lithium polyhydrides above 130 GPa at 300 K. Proc. Natl. Acad. Sci. USA 112, 7673 (2015).
Zhao, Z. et al. Pressure-induced stable Li5P for high-performance lithium-ion batteries. J. Phys. Chem. C 121, 21199–21205 (2017).
Zhao, Z. et al. Predicted pressure-induced superconducting transition in electride Li6P. Phys. Rev. Lett. 122, 097002 (2019).
Nazri, G. Preparation, structure and ionic conductivity of lithium phosphide. Solid State Ion. 34, 97–102 (1989).
Mayo, M. et al. Ab initio study of phosphorus anodes for lithium- and sodium-ion batteries. Chem. Mater. 28, 2011–2021 (2016).
Ma, Y. et al. Divergent synthesis routes and superconductivity of ternary hydride MgSiH6 at high pressure. Phys. Rev. B 96, 144518 (2017).
Ma, Y. et al. Prediction of superconducting ternary hydride MgGeH6: from divergent high-pressure formation routes. Phys. Chem. Chem. Phys. 19, 27406–27412 (2017).
Oganov, A. R. & Glass, C. W. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J. Chem. Phys. 124, 244704 (2006).
Lyakhov, A. O. et al. New developments in evolutionary structure prediction algorithm USPEX. Comput. Phys. Commun. 184, 1172–1182 (2013).
Pickard, C. J. & Needs, R. J. Structure of phase III of solid hydrogen. Nat. Phys. 3, 473 (2007).
Bader, R. F. W. Atoms in molecules. Acc. Chem. Res. 18, 9–15 (1985).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comput. Mater. Sci. 6, 15–50 (1996).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865 (1996).
Kresse, G. & Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 59, 1758 (1999).
Giannozzi, P. et al. QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials. J. Phys. Condens. Matter 21, 395502 (2009).
Allen, P. B. & Dynes, R. C. Transition temperature of strong-coupled superconductors reanalyzed. Phys. Rev. B 12, 905 (1975).
Akahama, Y., Kobayashi, M. & Kawamura, H. Simple-cubic-simple-hexagonal transition in phosphorus under pressure. Phys. Rev. B 59, 8520–8525 (1999).
Lv, J. et al. Predicted novel high-pressure phases of lithium. Phys. Rev. Lett. 106, 015503 (2011).
Acknowledgements
This work was supported by the National Key R&D Program of China (No. 2018YFA0305900), National Natural Science Foundation of China (Nos. 51632002, 11674122, 51572108, 11634004, 11504127, 11574109, 11704143, 11404134), Program for Changjiang Scholars and Innovative Research Team in University (No. IRT_15R23), the 111 Project (No. B12011). Parts of calculations were performed in the High Performance Computing Center (HPCC) of Jilin University and TianHe-1(A) at the National Supercomputer Center in Tianjin.
Author information
Authors and Affiliations
Contributions
T.C. and D.D. designed this projected. Z.S. performed the calculations. D.D. and Z.S. made the analysis and wrote the manuscript. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons license, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons license and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this license, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Shao, Z., Duan, D., Ma, Y. et al. Ternary superconducting cophosphorus hydrides stabilized via lithium. npj Comput Mater 5, 104 (2019). https://doi.org/10.1038/s41524-019-0244-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41524-019-0244-6
- Springer Nature Limited