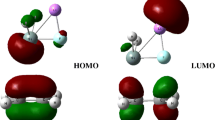
Abstract
Fixation and functionalisation of N2 by main-group elements has remained scarce. Herein, we report a fixation and cleavage of the N ≡ N triple bond achieved in a dinitrogen (N2) matrix by the reaction of hydrogen and laser-ablated silicon atoms. The four-membered heterocycle H2Si(μ-N)2SiH2, the H2SiNN(H2) and HNSiNH complexes are characterized by infrared spectroscopy in conjunction with quantum-chemical calculations. The synergistic interaction of the two SiH2 moieties with N2 results in the formation of final product H2Si(μ-N)2SiH2, and theoretical calculations reveal the donation of electron density of Si to π* antibonding orbitals and the removal of electron density from the π bonding orbitals of N2, leading to cleave the non-polar and strong NN triple bond.
Similar content being viewed by others
Introduction
The industrial synthesis of NH3 relies on the transition metal-catalyzed Haber-Bosch process1,2,3, in which the inert dinitrogen is converted to ammonia under harsh reaction conditions. This N≡N triple bond activation is based on partially filled d-orbitals of the d-block elements (e.g., Fe), which have a suitable symmetry and energy. An alternative way to activate dinitrogen is through main-group element compounds via the π back-donation from either the d orbitals (Ca, Sr, Ba) or p orbitals (Be, B, C)4. Wherein p-block elements (e.g., B and C) have a non-bonding (donor) electron pair and an energetically low-lying vacant (acceptor) orbital which can mimic the d-orbital character to activate dinitrogen5,6,7. Recently the p-block element boron was successfully used to activate dinitrogen8,9,10. Five- and seven-electron boron-centered radicals (R2B•) are predicted to be favorable for dinitrogen activation both thermodynamically and kinetically11,12. A crucial metric for nitrogen activation of substantially elongated N–N bond has been achieved by a borylene coordinating an N2 molecule in an end-on bridging position as [{(CAAC)-DurB}2(μ2-N2)] (CAAC = cyclic alkylamino carbene, Dur = 2,3,5,6-tetramethylphenyl)13,14,15. Our groups reported a complete cleavage of the N≡N triple bond by fluoroborylene (:BF) which has been observed as a cyclic FB(μ-N)2BF system in a matrix-isolation investigation under cryogenic conditions16. Carbene, another reactive intermediate, has also been used for N2 activation and conversion17,18,19. Maier et al. found that singlet σ0π2 carbene (2-diazo-2H-imidazole) would bind with dinitrogen in the matrix, demonstrating the potential for σ0π2 carbene to activate dinitrogen20. Furthermore, N2 activation by a carbene pair has been calculated and the N≡N triple bond was predicted to be elongated to an N-N single bond (1.428 Å) under the synergistic effect of the two CH2 moieties21. Silylene, the silicon analog of carbene, has been proven to exhibit similar properties to transition metal compounds, as it has a narrow HOMO-LUMO energy gap, which has received particular attention for the activation of small molecules22. As reported in 1998, the first isolable N-heterocyclic silylene reacts rapidly with dry O2, giving rise to a colorless and insoluble disiladioxetane polymer23. From then on, many small stable molecules, such as CO224, H2O25, P426, C2H427, H228, NH329, and C-H bonds30 have been activated by silylenes (see Fig. 1). In 2019 the splitting and reductive homocoupling of CO was achieved using the bis-silylenes (LSi:)2Xant [Xant = 9,9-dimethylxanthene-4,5-diyl; L = PhC(NtBu)2] and (LSi:)2Fc (Fc = 1,10-ferrocenyl)31. So far, only homoleptic N2 complexes of silicon have been reported under matrix-isolation conditions, including SiNN, Si(NN)232, and larger silicon-nitrogen clusters33,34, but the activation of more inert nitrogen by silylenes remain a challenge, although silylenes do exhibit high reactivity for other small molecules24,25,26,27,28,29,30,31. The key difficulty in silylene-mediated nitrogen activation is to modify the occupied and vacant orbitals of silylene in space and energy, which could enhance the weakening and functionalization of an inert chemical bond. For example, Driess et al. reported that two silylene moieties (bis-silylenes) could be cooperative in cleaving unreactive bonds, in which the Si---Si distance plays a crucial role31,35.
Here we report on the activation of dinitrogen by silylenes under cryogenic conditions. In our matrix-isolation experiments, laser-ablated silicon atoms have been reacted with H2, D2, HD, and H2/D2 mixtures in solid nitrogen that served as both reactant and host-matrix material. H2Si(μ-N)2SiH2 (A) is spectroscopically and quantum-chemically characterized, which demonstrates that the N2 triple bond is cleaved by the synergistic interaction of the two SiH2 moieties. In addition H2SiNN(H2) (B) and HNSiNH (C) are identified.
Results
Figures 2 and 3 show infrared spectra obtained after the laser-ablation of Si atoms co-deposited with a 10 % H2/N2 mixture at 4 K in a dinitrogen matrix. Further details are provided in the Supplementary Information (Supplementary Figs. 1–6). Isotopic experiments with H2, D2, HD, and H2/D2 samples in pure 14N2, 15N2, and 14/15N2 mixtures together with frequency calculations at the DFT level were used for the product identification (see Table 1 and Supplementary Tables 1–6). The EDA-NOCV method was used to elucidate the peculiar stability of the bonding nature. In addition to the three adduct products A, B, and C, H2SiNN, Si(NN)2, and SiNN have been observed (Fig. 1 and Supplementary Tables 1, 7)32,36,37. The absorptions associated with three silicon-nitrogen hydrides H2Si(μ-N)2SiH2 (A), H2SiNN(H2) (B), and HNSiNH (C) were unambiguously assigned based on their growth/decay behavior in different experiments and on their characteristic H/D and 14/15N isotope pattern. The absorptions for silicon nitrides and hydrides such as SiNN, Si(NN)2, SiH2, and SiH4 have been reported previously and agree with our assignments (Supplementary Figs. 7, 8)32,38,39.
The absorptions of the cyclic species A were observed upon λ > 220 nm irradiation and increased markedly upon the second λ > 220 nm irradiation (Fig. 2). The symmetric and antisymmetric D-Si-D modes were observed at 1551.3 and 1586.1 cm–1, respectively (Fig. 3b and Supplementary Fig. 1). Only the symmetric H-Si-H mode at 2165.3 cm−1 can be detected, leading to a H/D ratio of 1.3958. This observation is most likely due to a strong SiH4 band that covers the antisymmetric mode. In addition, the strongest absorption at 937.8 cm−1 of the H-Si-H bending mode shifted to 679.2 cm−1 in the deuterium experiment (H/D isotopic ratio 1.3807) (Fig. 3b and Supplementary Fig. 1), and in the 15N2 experiment a slight shift of 0.6 to 937.2 cm−1 was observed (Fig. 3d and Supplementary Fig. 4). Furthermore, a band for species A at 855.3 cm−1 in the D2/14N2 experiment (Fig. 3b) shifted by 20.6 to 834.7 cm−1 in the D2/15N2 experiment (Fig. 3f and Supplementary Fig. 6), which results in a 14N/15N ratio of 1.0247. The band can be assigned to the Si-N-Si stretching mode. The corresponding H2/14N2 experiment shows a band at 857.7 cm–1 (Fig. 3a). Its counterpart in the H2/15N2 experiment was covered by a broad signal of Si2H6 centered at 835.4 cm−1 (Fig. 3d and Supplementary Fig. 4).
When the isotopologues HD or a mixture of 5% H2 and 5% D2 as a hydrogen source were used, band distributions were observed for the bands of species A (Fig. 3c and Supplementary Figs. 2, 3). There are four possible isomers of A (A3, A4, A5, and A6) relating to 2H and 2D (see Supplementary Tables 1, 2). The 15% HD/14N2 experiment shows bands at 2167.4 and 2162.4 cm–1 (Si-H symmetric vibration), 1580.1, 1575.8, 1556.8, and 1550.5 cm–1 (Si-D vibration), 847.5 and 845.3 cm–1 (SiHD bend) which correspond to the isomers A4 (2167.4, 1575.8, and 847.5 cm–1), A5 (1556.8 and 845.3 cm–1) and A6 (1580.1, 1550.5, and 845.3 cm–1). The experiments using a mixture of 5% H2/5% D2 in 14N2 show three main isomers A1, A2, A3 with four groups of double bands at 2165.3 and 2163.0 cm–1 (Si-H vibration), 1586.1, 1577.2, 1551.3, and 1549.2 cm–1 (Si-D vibration), 946.4 and 937.8 cm–1 (SiH2 and SiD2 bend), 857.7 and 855.3 cm–1(Si(NN)Si ring); among these the bands at 2163.0, 1577.2, 1549.2, and 946.4 cm–1 can be attributed to A3. All bands are listed in Table 1 and Supplementary Tables 1–3. The identification of molecule A is also based on the excellent agreement of the observed and calculated frequencies at the CCSD(T) and B3LYP level of theory.
The calculated N–N distance in A is 1.828 Å at the B3LYP level (Fig. 4), which is significantly longer than the N–N single bond of diphenylhydrazine [d(N-N): 1.394 Å]40. A Mayer bond order of the N–N bond for molecule A is 0.689 computed at the B3LYP/6-311 G(3df,3pd) level. This suggests that the N≡N triple bond is cleaved by the two SiH2 units. The resonance structures of compound A have been provided by NBO-based Natural Resonance Theory (NRT) analysis (Supplementary Fig. 9)41,42,43. The ring inversion barrier of the puckered ring system of A was computed to be 6.2 kcal mol–1 at the B3LYP/6-311 + + G (3df, 3pd) level (Supplementary Fig. 10). As known from other cyclic main-group species, aromaticity is an important factor to stabilize both the transition state and the product during the N2 fixation process. To evaluate the compound’s aromaticity, computational chemistry is an effective tool44,45, and the aromaticity of the four-membered ring in A has been confirmed by the multi-center bond order (MCBO) indexes, gauge including magnetically induced current (GIMIC)46,47, the nucleus-independent chemical shift (NICS)48 and the electron density of delocalized bonds (EDDB)49,50 analyses. MCBO index, which is also known as the multi-center index (MCI) to evaluate aromaticity from the aspect of electron delocalization properties51,52,53. The MCBO index of A is 0.3046, similar to that of FB(μ-N)2BF (0.3190), which also has an aromatic four-membered B2N2 ring16. GIMIC method was calculated at B3LYP/6-311 + +g (3df, 3pd) level and a net diamagnetic ring current of 11.4 nA T–1 in A similar to the typical aromatic molecule benzene (11.8 nA T–1)54 could demonstrate the aromaticity of complex A (Supplementary Fig. 11). What’s more, the isotropic magnetic shielding tensor has been the most popular index for measuring aromaticity55, and the average NICS(1)av index can serve as a probe of aromaticity in nonplanar molecular systems. (Supplementary Fig. 12)56. The large negative NICS(1)av and NICS(0) indexes of –29.0 and –39.1 obtained at the center of gravity of species A indicate its aromatic character. Canonical molecular orbital natural chemical shielding (CMO-NICS(1)ZZ)57 was calculated at B3LYP/ 6-311 + + G(3df,3pd) level to separate the σ and π contributions of canonical molecular orbital, and larger diatropic contribution of –14.6 ppm from σ orbitals compared with −11.9 ppm from π orbitals (Supplementary Fig. 13) indicates σ aromaticity dominated in A, consistent with the EDDB analysis where 1.55 electrons delocalization was calculated (Supplementary Table 8) which are comparable to the number of delocalized electrons in L2Si2P2 (L = PhC(NtBu)2, 1.77 electrons)58 and the tetraatomic boron specie (1.57 electrons)59 and σ aromaticity is also the dominant one (60%).
H2SiNN(H2) (B) shows absorptions at 3569.3, 1991.6, 1983.6, 1097.5, and 952.4 cm−1 which appeared already upon codeposition (Fig. 2) and markedly increased upon λ > 300 nm irradiation with the obvious reduction of the SiNN. It decreased by 60% upon λ > 220 nm irradiation. The strong bands at 1991.6, 1983.6, and 952.4 cm−1 are assigned to the Si-H stretching and bending modes of the SiH2 subunit, which shifted to 1425.9, 1421.8, 684.4 cm−1 in the deuterium experiment (Fig. 3b and Supplementary Fig. 1), giving isotopic frequency ratios of 1.3967, 1.3951, and 1.3916, respectively. Moreover, two weak bands located at 3569.3 and 1097.5 cm−1 have been observed with H2, which shift to 2530.6 and 804.4 cm−1 with D2, exhibiting a H/D ratio of 1.4105 and 1.3644. They can be assigned to an H-H stretching and bending mode (Supplementary Fig. 1). These bands appear at 3110.3, 3102.4, and 977.0 cm−1 in the HD sample (Supplementary Fig. 2). Some bands at 1987.2, 1984.5, 1425.3, and 830.0 cm−1 turn up in 5% H2/5% D2 or HD experiments (Fig. 3c and Supplementary Figs. 2, 3) and are assigned to a SiHD stretching and bending mode. All these results suggest that B contains one side-on coordinated H2 molecule. The computed frequencies of H2SiNN(H2) are provided in Table 1 and Supplementary Table 4 and show a very good agreement between theory and experiment. Furthermore, in low H2 concentrations (less than 2%), sharp bands at 2274.2, 2013.6, 2009.4, and 928.8 cm−1 were observed, which have been assigned to H2SiN2 (Supplementary Figs. 14, 15)36. As shown in Supplementary Fig. 16, with an increase of H2, these doublet bands disappear, and the absorptions of species B will strongly be enhanced. This suggests an additional H2 coordination to H2SiN2 and, therefore, built species B. The ν(Si-H) stretching for B at 1991.6 and 1983.6 cm–1 is lower than these modes for H2SiN2 and the ν(N-N) stretching is higher, which is in good agreement with the B3LYP and CCSD(T) calculations (Supplementary Tables 9, 10). We performed Tesla coil discharge experiments to confirm the assignment of compound B (Supplementary Figs. 17–19). The absorptions of compound B increased after annealing to 33 K at the expense of H2SiN2 (Supplementary Fig. 17) and became even more intense with the increase of H2 concentrations ranging from 0 to 10% (Supplementary Fig. 18). This proves that H2 plays an important role in coordinating to H2SiN2 to give species B. Compound B might be described as a pseudo SiH4 forming a very weak adduct with dinitrogen with a bond distance slightly shorter than the van der Waals distance of 3.7 Å and the N-N stretching frequency is too weak to be observed.
Two additional bands at 3564.8 and 1197.6 cm−1 assigned to a new molecule HNSiNH (C) have been observed by codeposition. They increased on both λ > 300 nm and λ > 220 nm irradiation at the expense of the absorptions of H2SiN2 and SiNN (see Fig. 2 and Supplementary Tables 5, 11). These bands belong to the N–H and N–Si–N stretching modes of the species HNSiNH. Additional isotope experiments were performed using a mixture of D2/N2. They show absorptions of the corresponding isotopologues at 2662.5 cm−1 (H/D isotopic ratio 1.3389), which is very close to the isotopic ratio of HNSi in a 4 K argon matrix (H/D isotopic ratio 1.3424)60, and at 1164.8 cm−1 (H/D isotopic ratio 1.0282), see Fig. 3b and Supplementary Fig. 1. With H2/15N2, the counterpart bands were observed at 3556.2 cm–1 (14N/15N isotopic ratio 1.0024) and 1175.9 cm−1 (14N/15N isotopic ratio 1.0186) also shown in Fig. 3d and Supplementary Fig. 4. With D2/15N2, the two bands shifted to 2647.3 and 1143.2 cm−1 (Fig. 3f and Supplementary Fig. 6). Moreover, in our HD experiment, a band at 1178.4 cm−1 reveals an isotopic triplet indicating the involvement of two equivalent hydrogen atoms (Fig. 3c and Supplementary Figs. 2, 3). The Si–N bond length of C, calculated to be 1.571 Å at the B3LYP level (Fig. 4), is much shorter than the Si–N single bond (1.87 Å) and is close to the N=Si bond in HN=Si (1.559 Å)61,62,63,64 and the N=Si monomer with a double bond of 1.572 Å65,66.
As shown in Fig. 5, SiNN (3Σ) was supposed to be a starting compound to give the complex H2SiNN (1A1) with H2 upon λ > 300 nm irradiation. In the next step, H2SiNN reacts with a second H2 molecule to form complex B. The corresponding barrier was computed to be only 1.8 kcal/mol at the DFT level, which is in accordance with the increase of H2SiNN and complex B and the decrease of SiNN upon λ > 300 nm irradiation. Although H2Si: could not be observed directly in the spectrum, it can still be assumed that H2Si: is formed either in the reaction of silicon with hydrogen or via SiHx decomposition, and in a dinitrogen atmosphere will further react with N2 or N2 and H2 to form H2SiNN and H2SiNN(H2). Further reaction of H2SiNN(H2) with SiNN forms the H2Si(μ-N)2SiH2 (A) complex through hydrogen transfer, forming two SiH2 subunits and finally leading to an NN triple bond cleavage (Fig. 5 and Supplementary Figs. 20–22). In principle, the cryogenic conditions of the matrix provide a good environment in that both H2SiNN(H2) and SiNN synergistically react as Lewis bases and initiate a step-wise reduction of the N2 moiety. In the Tesla coil discharge reactions of SiH4 with or without H2 in excess solid N2, both H2SiN2 and species B can be observed, while species A is missing due to the lack of SiNN (Supplementary Fig. 23g–i). In the reactions of laser-ablated Si atoms with 10% SiH4 in solid nitrogen, species A is also not generated because of the absence of species B. This shows that both B and SiNN are essential for the formation of product A (Supplementary Fig. 23d–f).
Based on quantum-chemical calculations, the nitrogen atoms in A show a more negative partial charge of –1.07 e, while the Si atoms carry a more positive partial charge of 1.45 e compared to compound B (Supplementary Table 12). As shown at the energy surface (Fig. 5), A is computed to be exothermic by 114.6 kcal mol–1 with the highest activation barrier of 38.4 kcal mol–1. Note that the activation of CO to react to the ethynediolate dianion [OCCO]2– has been achieved by a bis-silylene31. In addition, SiNN (1A1, C2v) also leads to the formation of C, with an activation barrier of 32.8 kcal mol–1. C is observed in freshly deposited samples, and it increased markedly after λ > 220 nm irradiation, in which the laser-ablated energy provided in the codeposition process and the irradiation energy at λ > 220 nm most likely support the formation separately. SiNN (1A1, C2v) reacts with H2 to form H2SiN2 and then isomerizes to C through H transfer and N-N bond cleavage (Fig. 6 and Supplementary Figs. 24, 25). Similar exothermic reactions could occur when H-substituted groups, such as CH3 and Ph, are applied (Supplementary Fig. 26). Similar to NHC1-H67, H2Si displays the smallest singlet–triplet energy gap and lowest ΔE to give H2SiNN, showing the great potential for dinitrogen activation.
The EDA-NOCV method was used to elucidate the peculiar stability of the bonding nature in A. As shown in Fig. 7 the neutral fragments N2 (1Ʃg) and (SiH2)2 (1A) in the singlet state, which refer to the symmetry-allowed dissociation products, have been selected as interacting moieties that address the question about all changes along the bond formation between two neutral fragments68. The numerical results are shown in Supplementary Table 13 and the breakdown of the orbital interaction into pairwise orbital interactions reveals that the dominant orbital stabilization, ΔEorb(1) (–329.1 kcal mol–1) and ΔEorb(2) (–318.7 kcal mol–1) comes from the back-donation of the HOMO-1 (mainly 3px of the Si atom) and the HOMO (mainly 3px of the Si atom) of the (SiH2)2 moiety into the two perpendicular π* MOs of the N2 ligands, known as push effect. The most interesting orbital interactions are ΔEorb(3) and ΔEorb(4), which contribute to the donation of π MO electrons of the N2 ligands to the LUMO + 1 (3pz of Si atom and 1 s of H atom) and LUMO (mainly 3s, 3py, 3pz, and 4s of Si atom) of the (SiH2)2 fragment (pull effect). This is unlike the end-on complex H2SiNN42,43 with a σ-donation and a π back-donation, in which the σ-donation only plays a bonding role for the Si-N bond. However, for complex A, H2Si: shows both interactions, which donates electron density to π*-antibonding orbitals of N2 and removes electron density from the π-bonding orbitals of N2 and, therefore, cooperatively cleaves the NN triple bond69. In addition, our EDA-NOCV results are illustrated in Supplementary Table 14 for A using neutral and charged fragments as interacting moieties. The smallest ΔEorb values are found when the doubly charged species (SiH2)22+ (3A) and (N2)2- (3∑g) are used for the calculations, which is a measure for the best description of the bonds finally formed70,71. The orbital term ΔEorb accounts for 70% of the total attraction between the neutral units. However, the dominance of covalent bonding disappears when the final bonding situation is analyzed. The electrostatic part of the attractive interactions constitutes greater than 50% of the total attraction. The shape of the deformation densities, Δρ(1)-(4) of H2Si(μ-N)2SiH2 using (SiH2)22− and N22− as interacting fragments were shown in Supplementary Fig. 27. When the bond finally formed, (SiH2)22+ (3B2) and (N2)2− (3∑g) still basically follow the rules of “push and pull”, but the donation from N22− is stronger.
In this work, three activated dinitrogen species, H2Si(μ-N)2SiH2, H2SiNN(H2), and HNSiNH, have been identified by isotopic substitution experiments under cryogenic conditions in matrix-isolation experiments in conjunction with quantum-chemical calculations. The N≡N triple bond was activated and broken by the synergistic interaction of two SiH2 moieties in low-temperature matrix circumstances to form the stable aromatic ring system Si2N2. The SiNN is supposed to be an important starting compound to form the complex H2SiNN(H2) (B) with H2, which then further reacts with SiNN to build the final product H2Si(μ-N)2SiH2 (A). The EDA-NOCV calculations support a dual interaction of H2Si, which is able to donate electron density to π*-antibonding orbitals of N2 and remove electron density from the π-bonding orbitals, leading to the cleavage of the N2 triple bond and the formation of H2Si(μ-N)2SiH2. This research work might open a different way to functionalize and activate dinitrogen molecules.
Methods
Matrix-isolation experiments
A Nd:YAG laser fundamental(1064 nm, 10 Hz repetition rate with 10 ns pulse width and 20−50 mJ/pulse) was focused on a rotating silicon target (Alfa Aesar), generating a bright plume. The laser-ablated silicon atoms reacting with H2, D2, HD, and H2 + D2 mixtures in solid N2 and 15N2, were condensed at 4 K using a closed-cycle helium refrigerator (Sumitomo Heavy Industries Model SRDK-408D2). Infrared spectra were recorded on a Bruker 80 v spectrometer at 0.5 cm−1 resolution between 4000 and 400 cm−1 using a HgCdTe range B detector. Further experimental details are provided in the Supplementary Information.
Quantum chemistry calculation
All of the structures were optimized at Post-HF (CCSD(T)) and complementary density functional theory (DFT) methods and the vibration frequencies were computed analytically via Gaussian 09 program72. The bonding nature in A was investigated using energy decomposition analysis (EDA) combined with the natural orbitals for the chemical valence (NOCV) method. The analyses for the aromaticity were calculated with the Gaussian 09 program, the Multiwfn code53, NBO 6.0 program57, GIMIC2.0 program47,73, and the RunEDDB program49,50, respectively. Further quantum-chemical details are provided in the Supplementary Information.
Data availability
All data generated in this study are provided in the Article and Supplementary Information. The experiment data that support the findings of this study are available from the corresponding author upon request.
Change history
24 May 2024
A Correction to this paper has been published: https://doi.org/10.1038/s41467-024-48898-7
References
Chen, J. G. et al. Beyond fossil fuel-driven nitrogen transformations. Science 360, eaar6611 (2018).
Falcone, M., Chatelain, L., Scopelliti, R., Zivkovic, I. & Mazzanti, M. Nitrogen reduction and functionalization by a multimetallic uranium nitride complex. Nature 547, 332–335 (2017).
MacLeod, K. C. & Holland, P. L. Recent developments in the homogeneous reduction of dinitrogen by molybdenum and iron. Nat. Chem. 5, 559–565 (2013).
Liu, T. T., Zhai, D. D., Guan, B. T. & Shi, Z. J. Nitrogen fixation and transformation with main group elements. Chem. Soc. Rev. 51, 3846–3861 (2022).
Melen, R. L. Frontiers in molecular p-block chemistry: from structure to reactivity. Science 363, 479–484 (2019).
Guo, F. S., Bar, A. K. & Layfield, R. A. Main group chemistry at the interface with molecular magnetism. Chem. Rev. 119, 8479–8505 (2019).
Power, P. P. Main-group elements as transition metals. Nature 463, 171–177 (2010).
Légaré, M.-A., Pranckevicius, C. & Braunschweig, H. Metallomimetic chemistry of boron. Chem. Rev. 119, 8231–8261 (2019).
Broere, D. L. J. & Holland, P. L. Boron compounds tackle dinitrogen. Science 359, 871–871 (2018).
Braunschweig, H. et al. Multiple complexation of CO and related ligands to a main-group element. Nature 522, 327–330 (2015).
Zeng, J., Dong, S. C., Dai, C. S. & Zhu, J. Predicting dinitrogen activation by five-electron boron-centered radicals. Inorg. Chem. 61, 2234–2241 (2022).
Zeng, J., You, F. Y. & Zhu, J. Screening seven-electron boron-centered radicals for dinitrogen activation. J. Comput. Chem. 45, 648–654 (2024).
Légaré, M.-A. et al. Nitrogen fixation and reduction at boron. Science 359, 896–899, (2018).
Légaré, M.-A. et al. The reductive coupling of dinitrogen. Science 363, 1329–1332 (2019).
Légaré, M.-A. et al. One-pot, room-temperature conversion of dinitrogen to ammonium chloride at a main-group element. Nat. Chem. 12, 1076–1080 (2020).
Xu, B. et al. Cleavage of the N≡N triple bond and unpredicted formation of the cyclic 1,3-diaza-2,4-diborete (FB)2N2 from N2 and fluoroborylene BF. Angew. Chem. Int. Ed. 60, 17205–17210 (2021).
Wang, C. H., Yin, Z. B., Wei, J. N., Zhang, W. X. & Xi, Z. F. Outlook of nitrogen fixation by carbene. Tetrahedron 76, 131703 (2020).
Moore, C. B. & Pimentel, G. C. Matrix reaction of methylene with nitrogen to form diazomethane. J. Chem. Phys. 41, 3504–3509 (1964).
Shilov, A. E., Shteinman, A. A. & Tjabin, M. B. Reaction of carbenes with molecular nitrogen. Tetrahedron Lett. 9, 4177–4180 (1968).
Maier, G. & Endres, J. 2H-imidazol-2-ylidene: new insights from a matrix-spectroscopic study. Chem. Eur. J. 5, 1590–1597 (1999).
Khan, S. N., Kalernos, A. & Miliordos, E. Metal-free activation of N2 by persistent carbene pairs: an ab initio investigation. J. Phys. Chem. C. 123, 21548–21553 (2019).
Shan, C. K., Yao, S. L. & Driess, M. Where silylene-silicon centres matter in the activation of small molecules. Chem. Soc. Rev. 49, 6733–6754 (2020).
Haaf, M. et al. Synthesis and reactivity of a stable silylene. J. Am. Chem. Soc. 120, 12714–12719 (1998).
Jutzi, P., Eikenberg, D., Möhrke, A., Neumann, B. & Stammler, H.-G. Decamethylsilicocene chemistry: unprecedented multistep reactions of a silicon(II) compound with the heterocumulenes CO2, COS, CS2, and RNCS (R=methyl, phenyl). Organometallics 15, 753–759 (1996).
Haaf, M., Schmedake, T. A., Paradise, B. J. & West, R. Synthesis and reactivity of the stable silylene N, N’-di-tert-butyl-1,3-diaza-2-sila-2-ylidene. Can. J. Chem. 78, 1526–1533 (2000).
Xiong, Y., Yao, S., Brym, M. & Driess, M. Consecutive insertion of a silylene into the P4 tetrahedron:: facile access to strained SiP4 and Si2P4 cage compounds. Angew. Chem. Int. Ed. 46, 4511–4513 (2007).
Rodriguez, R. et al. Reversible binding of ethylene to silylene-phosphine complexes at room temperature. Angew. Chem. Int. Ed. 50, 10414–10416 (2011).
Protchenko, A. V. et al. A stable two-coordinate acyclic silylene. J. Am. Chem. Soc. 134, 6500–6503 (2012).
Hadlington, T. J., Abdalla, J. A. B., Tirfoin, R., Aldridge, S. & Jones, C. Stabilization of a two-coordinate, acyclic diaminosilylene (ADASi): completion of the series of isolable diaminotetrylenes,:E(NR2) 2 (E = group 14 element). Chem. Commun. 52, 1717–1720 (2016).
Kira, M., Ishida, S., Iwamoto, T. & Kabuto, C. Excited-state reactions of an isolable silylene with aromatic compounds. J. Am. Chem. Soc. 124, 3830–3831 (2002).
Wang, Y. W. et al. Silicon-mediated selective homo- and heterocoupling of carbon monoxide. J. Am. Chem. Soc. 141, 626–634 (2019).
Maier, G., Reisenauer, H. P. & Glatthaar, J. Reactions of silicon atoms with nitrogen: a combined matrix spectroscopic and density functional theory study. Organometallics 19, 4775–4783 (2000).
Brugh, D. J. & Morse, M. D. Resonant two-photon ionization spectroscopy of the 13-electron triatomic Si2N. Chem. Phys. Lett. 267, 370–376 (1997).
Meloni, G., Cesaro, S. N. & Sanna, N. FTIR matrix isolation and ab initio investigations of the Si2N and BNSi molecules. Chem. Phys. Lett. 343, 113–118 (2001).
Luecke, M. P., Pens, E., Yao, S. L. & Driess, M. An isolable bis(silanone-borane) adduct. Chem. Eur. J. 26, 4500–4504 (2020).
Amicangelo, J. C. et al. Matrix isolation infrared observation of HxSi(N2)y(x=0, 1, 2 and y =1, 2) transient species using a 121-nm vacuum ultraviolet photolysis source. J. Phys. Chem. A 112, 3020–3030 (2008).
Maier, G., Reisenauer, H. P., Glatthaar, J. & Zetzmann, R. Complex of silylene with nitrogen: a combined matrix-spectroscopic and density functional theory study. Chem. Asian J. 1, 195–202 (2006).
Andrews, L. & Wang, X. F. Infrared spectra of the novel Si2H2 and Si2H4 species and the SiH1,2,3 intermediates in solid neon, argon, and deuterium. J. Phys. Chem. A 106, 7696–7702 (2002).
Fredin, L., Hauge, R. H., Kafafi, Z. H. & Margrave, J. L. Matrix isolation studies of the reactions of silicon atoms with molecular hydrogen. The infrared spectrum of silylene. J. Chem. Phys. 82, 3542–3545 (1985).
Pestana, D. C. & Power, P. P. Synthesis and structure of diarylboryl-substituted hydrazines and diphosphanes: role of σ-orbital hybridization and π-orbital overlap in N-N and P-P multiple-bond lengths. Inorg. Chem. 30, 528–535 (1991).
Glendening, E. D. & Weinhold, F. Natural resonance theory: I. General formalism. J. Comput. Chem. 19, 593–609 (1998).
Glendening, E. D. & Weinhold, F. Natural resonance theory: II. Natural bond order and valency. J. Comput. Chem. 19, 610–627 (1998).
Glendening, E. D., Badenhoop, J. K. & Weinhold, F. Natural resonance theory: III. Chemical applications. J. Comput. Chem. 19, 628–646 (1998).
Zhu, J. Rational design of a carbon-boron frustrated Lewis pair for metal-free dinitrogen activation. Chem. Asian J. 14, 1413–1417 (2019).
Zhu, Q. et al. The application of aromaticity and antiaromaticity to reaction mechanisms. Fundam. Res. 3, 926–938 (2023).
Jusélius, J., Sundholm, D. & Gauss, J. Calculation of current densities using gauge-including atomic orbitals. J. Chem. Phys. 121, 3952–3963 (2004).
Fliegl, H., Taubert, S., Lehtonen, O. & Sundholm, D. The gauge including magnetically induced current method. Phys. Chem. Chem. Phys. 13, 20500–20518 (2011).
Chen, Z. F., Wannere, C. S., Corminboeuf, C., Puchta, R. & Schleyer, P. V. Nucleus-independent chemical shifts (NICS) as an aromaticity criterion. Chem. Rev. 105, 3842–3888 (2005).
Szczepanik, D. W. et al. A uniform approach to the description of multicenter bonding. Phys. Chem. Chem. Phys. 16, 20514–20523 (2014).
Szczepanik, D. W. et al. The electron density of delocalized bonds (EDDB) applied for quantifying aromaticity. Phys. Chem. Chem. Phys. 19, 28970–28981 (2017).
Giambiagi, M., Giambiagi, M. S. D. & Mundim, K. C. Definition of a multicenter bond index. Struct. Chem. 1, 423–427 (1990).
Matito, E. An electronic aromaticity index for large rings. Phys. Chem. Chem. Phys. 18, 11839–11846 (2016).
Lu, T. & Chen, F. W. Multiwfn: a multifunctional wavefunction analyzer. J. Comput. Chem. 33, 580–592 (2012).
Fliegl, H., Sundholm, D., Taubert, S., Jusélius, J. & Klopper, W. Magnetically induced current densities in aromatic, antiaromatic, homoaromatic, and nonaromatic hydrocarbons. J. Phys. Chem. A 113, 8668–8676 (2009).
Hadjiivanov, K. I. et al. Power of infrared and Raman spectroscopies to characterize metal-organic frameworks and investigate their interaction with guest molecules. Chem. Rev. 121, 1286–1424 (2021).
Dobrowolski, J. C. & Lipiński, P. F. J. On splitting of the NICS(1) magnetic aromaticity index. Rsc. Adv. 6, 23900–23904 (2016).
Glendening, E. D. et al. NBO,6.0 (Wisconsin Univ., 2001).
Sen, S. S. et al. Zwitterionic Si-C-Si-P and Si-P-Si-P four-membered rings with two-coordinate phosphorus atoms. Angew. Chem. Int. Ed. 50, 2322–2325 (2011).
Dai, C. S., Huang, Y. Y. & Zhu, J. Adaptive σ aromaticity and triplet ground state in tetraatomic boron species. Organometallics 39, 2602–2608 (2020).
Ogilvie, J. F. & Cradock, S. Spectroscopic studies of the photodecomposition of silyl azides in argon matrices near 4°K: detection of iminosilicon, HNSi. Chem. Commun. 12, 364–365 (1966).
Pyykkö, P. & Atsumi, M. Molecular single-bond covalent radii for elements 1-118. Chem. Eur. J. 15, 186–197 (2009).
Pyykkö, P., Riedel, S. & Patzschke, M. Triple-bond covalent radii. Chem. Eur. J. 11, 3511–3520 (2005).
Maier, G. & Glatthaar, J. Silane nitrile: matrix isolation, adduct with hydrogen. Angew. Chem. Int. Ed. 33, 473–475 (1994).
Chen, M. H., Zheng, A. H., Lu, H. & Zhou, M. F. Reactions of atomic silicon and germanium with ammonia: a matrix-isolation FTIR and theoretical study. J. Phys. Chem. A 106, 3077–3083 (2002).
Bredohl, H., Dubois, I., Houbrechts, Y. & Singh, M. The emission spectrum of SiN. Can. J. Phys. 54, 680–688 (1976).
Owusu-Ansah, E., Wang, Y. M. & Shi, Y. J. A theoretical study of the structures and electronic transitions of small silicon nitride clusters (SinNm, n + m ≤ 4). J. Mol. Spectrosc. 330, 200–210 (2016).
Zeng, J., Su, J. Y., You, F. Y. & Zhu, J. Understanding reaction mechanisms of metal-free dinitrogen activation by methyleneboranes. Chin. Chem. Lett. 34, 107759 (2023).
Zhao, L., Pan, S., Holzmann, N., Schwerdtfeger, P. & Frenking, G. Chemical bonding and bonding models of main-group compounds. Chem. Rev. 119, 8781–8845 (2019).
Zhang, H. Y., Yuan, R., Wu, W. & Mo, Y. R. Two push-pull channels enhance the dinitrogen activation by borylene compounds. Chem. Eur. J. 26, 2619–2625 (2020).
Saha, R., Pan, S., Merino, G. & Chattaraj, P. K. Unprecedented bonding situation in viable E2(NHBMe)2 (E=Be, Mg; NHBMe=(HCNMe)2B) complexes: neutral E2 forms a single E-E covalent bond. Angew. Chem. Int. Ed. 58, 8372–8377 (2019).
Wang, Q. et al. Transition-metal chemistry of alkaline-earth elements: the trisbenzene complexes M(Bz)3 (M=Sr, Ba). Angew. Chem. Int. Ed. 58, 17365–17374 (2019).
Frisch, M. J. et al. Gaussian 09, revision A.1 (Gaussian, Inc., 2009).
Sundholm, D., Fliegl, H. & Berger, R. J. F. Calculations of magnetically induced current densities: theory and applications. WIREs Comput. Mol. Sci. 6, 639–678 (2016).
Acknowledgements
We gratefully acknowledge financial support from the National Natural Science Foundation of China (No. 22273066). Special thanks to Dr. Beckers for the generous discussions and support. Thanks are due to Hu Jin, Wen Liu, and Yan Lu for assistance with the calculation for aromaticity.
Author information
Authors and Affiliations
Contributions
B.X. and X.F.W. designed and supervised the matrix-isolation experiments and revised the manuscript. L.C. performed the experiments and the quantum-chemical calculations and wrote the draft. S.R. performed the quantum-chemical calculations and revised the manuscript. J.C and F.C. perform experiments partly.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interest.
Peer review
Peer review information
Nature Communications thanks Norihiro Tokitoh, Jun Zhu and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cai, L., Xu, B., Cheng, J. et al. N2 cleavage by silylene and formation of H2Si(μ-N)2SiH2. Nat Commun 15, 3848 (2024). https://doi.org/10.1038/s41467-024-48064-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-48064-z
- Springer Nature Limited