Skip to main content
SpringerLink
Log in

The Secondary Bifurcation of an Aeroelastic Airfoil Motion: Effect of High Harmonics

  • Published:
Nonlinear Dynamics Aims and scope Submit manuscript

Abstract

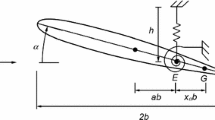
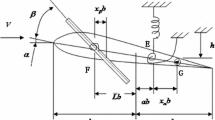
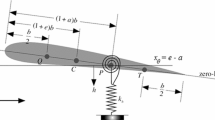
The nonlinear dynamical response of a two-degree-of-freedom aeroelastic airfoil motion with cubic restoring forces is investigated. A secondary bifurcation after the primary Hopf (flutter) bifurcation is detected for a cubic hard spring in the pitch degree-of-freedom. Furthermore, there is a hysteresis in the secondary bifurcation: starting from different initial conditions the motion may jump from one limit cycle to another at different fluid flow velocities. A high-order harmonic balance method is employed to investigate the possible bifurcation branches. Furthermore, a numerical time simulation procedure is used to confirm the stable and unstable bifurcation branches.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Woolston, D. S., Runyan, H. L., and Byrdsong, T. A., 'Some effects of system nonlinearities in the problem of aircraft flutter', NACA TN 3539, 1955.

  2. Lee, B. H. K. and LeBlanc, P., 'Flutter analysis of a two-dimensional airfoil with cubic nonlinear restoring force', National Research Council of Canada, Aeronautical Note, NAE-AN-36 NRC No. 25438, 1986.

  3. Houbolt, J. C., 'A recurrence matrix solution for the dynamic response of elastic aircraft', Journal of Aeronautical Sciences 17, 1950, 540–550.

    Google Scholar 

  4. O'Neil, T., Gilliatt, H., and Strganac, T., 'Investigation of aeroelastic response for a system with continuous structural nonlinearities', AIAA Paper 96-1390, 1996.

  5. Price, S. J., Alighanbari, H., and Lee, B. H. K., 'The aeroelastic response of a two-dimensional airfoil with bilinear and cubic structural nonlinearities', Journal of Fluids and Structures 9, 1995, 175–193.

    Article  Google Scholar 

  6. Krylov, N. and Bogoliubov, N., Introduction to Nonlinear Mechanics, translation by Solomon Lifschitz, Princeton University Press, Princeton, New Jersey, 1947.

    Google Scholar 

  7. Zhao, L. C. and Yang, Z. C., 'Chaotic motions of an airfoil with nonlinear stiffness in incompressible flow', Journal of Sound and Vibration 138, 1990, 245–254.

    Article  Google Scholar 

  8. Lee, B. H. K., Gong L., and Wong, Y. S., 'Analysis and computation of nonlinear dynamic response of a two-degree-offreedom system and its application in aeroelasticity', Journal of Fluids and Structures 11, 1997, 225–246.

    Article  Google Scholar 

  9. Lee, B. H. K., Jiang, L. Y., and Wong, Y. S., 'Flutter of an airfoil with a cubic nonlinear restoring force', Journal of Fluids and Structures 13, 1999, 75–101.

    Article  Google Scholar 

  10. Liu, L., Wong, Y. S., and Lee, B. H. K., 'Application of the center manifold theory in nonlinear aeroelasticity', Journal of Sound and Vibration 234, 2000, 641–659.

    Article  Google Scholar 

  11. Lee, B. H. K., Liu, L., and Chung, K. W., 'Airfoil motion in subsonic flow with strong cubic nonlinear restoring forces', Journal of Sound and Vibration (in press).

  12. Popov, E. P., 'On the use of the harmonic linearication method in automatic control theory', NACA TM 1406, 1957.

  13. Fung, Y. C., An Introduction to the Theory of Aeroelasticity, Dover, New York, 1969.

  14. Jones, R. T., 'The unsteady lift of a wing of finite aspect ratio', NACA Report 681, 1940.

  15. Rand, R. H. and Holmes, P. J., 'Bifurcation of periodic motions in two weakly coupled van der Pol oscillators', International Journal of Non-Linear Mechanics 15, 1980, 387–399.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Mechanical Engineering and Materials Science, Duke University, Durham, NC, 27708, U.S.A

    Liping Liu & Earl H. Dowell

Authors
  1. Liping Liu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Earl H. Dowell
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Liu, L., Dowell, E.H. The Secondary Bifurcation of an Aeroelastic Airfoil Motion: Effect of High Harmonics. Nonlinear Dynamics 37, 31–49 (2004). https://doi.org/10.1023/B:NODY.0000040033.85421.4d

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/B:NODY.0000040033.85421.4d

Search

Navigation