Optimal allocation procedure in ranked set sampling for unimodal and multi-modal distributions

Abstract

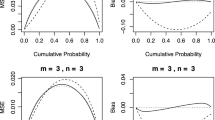
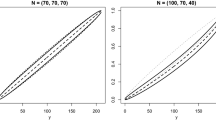
This paper presents a ranked set sample allocation procedure that is optimal for a number of nonparametric test procedures. We define a function that measures the amount of information provided by each observation given the actual joint ranking of all the units in a set. The optimal ranked set sample allocates order statistics by maximizing this information function. This paper shows that the optimal allocation of order statistics in a ranked set sample is determined by the location of the mode(s) of the underlying distribution. For unimodal, symmetric distributions, optimal allocation always quantifies the middle observation(s). If the underlying distribution with cdf F is a multi-modal distribution with modes $R, \ldots ,R_k$, then the optimal allocation procedure quantifies observations at $mF(R_1 ), \ldots ,mF(R_1 )$ in a set of size m. We provide similar results for unimodal, asymmetric distributions. We also propose a new sign test which considers the relative positions of the quantified observations from the same cycle in a ranked set sample. The proposed sign test provides improvement in the Pitman efficiency over the ranked set sample sign test of Hettmansperger (1995). It is shown that the information optimal allocation procedure induced by Pitman efficiency is equivalent to the optimal allocation procedure induced by the information criteria. We show that the finite sample distribution of the proposed test based on this optimal design is binomial.