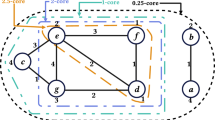
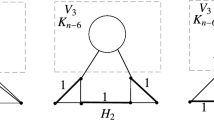
Abstract
We consider the MAX \(\frac{n}{{\text{2}}}\)-DIRECTED-BISECTION problem, i.e., partitioning the vertices of a directed graph into two blocks of equal cardinality so as to maximize the total weight of the edges in the directed cut. A polynomial approximation algorithm using a semidefinite relaxation with 0.6458 performance guarantee is presented for the problem. The previous best-known results for approximating this problem are 0.5 using a linear programming relaxation, 0.6440 using a semidefinite relaxation. We also consider the MAX \(\frac{n}{{\text{2}}}\)-DENSE-SUBGRAPH problem, i.e., determine a block of half the number of vertices from a weighted undirected graph such that the sum of the edge weights, within the subgraph induced by the block, is maximized. We present an 0.6236 approximation of the problem as opposed to 0.6221 of Halperin and Zwick.
Similar content being viewed by others
References
Ageev, A., Hassin, R., and Sviridenko M. (2001), An 0.5-approximation algorithm for the max dicut with given sizes of parts, SIAM J. Discrete Math. 14, 246–255.
Bertsimas, D. and Ye, Y. (1998), Semidefinite relaxations, multivariate normal distributions, and order statistics. In: Du, D. Z. and Pardalos, P.M. (eds.), Handbook of Combinatorial Optimization (Vol. 3), pp. 1–19, Kluwer Academic Publishers.
Feige, U. and Goemans, M. X. (1995), Approximating the value of two prover proof systems, with applications to MAX 2SAT and MAX DICUT. In: Proceedings of the 3rd Israel Symposium on Theory and Computing Systems, Tel Aviv, Israel, pp. 182–189.
Feige, U. and Langberg, M. (1999), Approximation algorithms for maximization problems arising in graph partitioning, Manuscript and M. Sc. thesis.
Frieze, A. and Jerrum, M. (1997), Improved approximation algorithms for max k-cut and max bisection, Algorithmica 18, 67-81.
Feige, U. and Seltser, M. (1997), On the densest k-subgraph problem, Technical Report, Department of Applied Mathematics and Computer Science, The Weizmann Institute, Rehovot.
Goemans, M. X. (1996), Mathematical programming and approximation algorithms, Lecture given at the Summer School on Approximate Solution of Hard Combinatorial Problems, Udine.
Goemans, M. X. and Williamson, D. P. (1995), Improved approximation algorithms for Maximum Cut and Satisfiability problems using semidefinite programming, Journal of ACM 42, 1115–1145.
Halperin, E. and Zwick, U. (2001), A unified framework for obtaining improved approximation algorithms for maximum graph bisection problems, Manuscript.
Han, Q., Ye, Y., Zhang, H., and Zhang, J. (2002), On approximation of Max-Vertex-Cover, to appear in European Journal of Operational Research.
Han, Q., Ye, Y., and Zhang, J. (2002), An improved rounding method and semidefinite programming relaxation for graph partition, Math. Program. 92, 509–535.
Lovasz, L. and Shrijver, A. (1990), Cones of matrices and setfunctions, and 0-1 optimization, SIAM J. of Optimization 1, 166–190.
Mahajan, S. and Ramesh, H. (1999), Derandomizing approximation algorithms based on semidefinite programming, SIAM J. Comput. 28, 1641–1663.
Nesterov, Y. (1998), Semidefinite relaxation and nonconvex quadratic optimization, Optimization Methods and Software 9, 141–160.
Papadimitriou, C. H. and Yannakakis, M. (1991), Optimization, approximation, and complexity classes, J. Comput. Syst. Sci. 43, 425–440.
Srivastav, A. and Wolf, K. (1998), Finding dense subgraphs with semidefinite programming. In: Jansen, K. and Rolim, J. (eds.) Approximation Algorithms for Combinatorial Optimization, pp. 181–191.
Ye, Y. (2001), A.699-approximation algorithm for Max-Bisection, Math. Program. 90, 101–111.
Ye, Y. and Zhang, J. (2003), Approximation of dense-\(\frac{n}{{\text{2}}}\)-subgraph and the complement of min-bisection, Journal of Global Optimization 25, 55–73.
Zwick, U. (1999), Outward rotations: a tool for rounding solutions of semidefinite programming relaxations, with applications to max cut and other problems. In: Proceedings of the 30th Symposium on Theory of Computation (STOC), pp. 551–560.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Xu, D., Han, J., Huang, Z. et al. Improved Approximation Algorithms for MAX \(\frac{n}{{\text{2}}}\)-DIRECTED-BISECTION and MAX \(\frac{n}{{\text{2}}}\)-DENSE-SUBGRAPH. Journal of Global Optimization 27, 399–410 (2003). https://doi.org/10.1023/A:1026094110647
Issue Date:
DOI: https://doi.org/10.1023/A:1026094110647