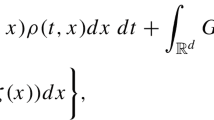Skip to main content
SpringerLink
Log in

Neumann Control of Unstable Parabolic Systems: Numerical Approach

  • Published:
Journal of Optimization Theory and Applications Aims and scope Submit manuscript

Abstract

The present article is concerned with the Neumann control of systems modeled by scalar or vector parabolic equations of reaction-advection-diffusion type with a particular emphasis on systems which are unstable if uncontrolled. To solve these problems, we use a combination of finite-difference methods for the time discretization, finite-element methods for the space discretization, and conjugate gradient algorithms for the iterative solution of the discrete control problems. We apply then the above methodology to the solution of test problems in two dimensions, including problems related to nonlinear models.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Keller, H. B., and Langford, W. F., Iterations, Perturbations, and Multiplicities for Nonlinear Bifurcation Problems, Archives for Rational Mechanics and Analysis, Vol. 48, pp. 83–108, 1972.

    Google Scholar 

  2. Keener, J. P., and Keller, H. B., Perturbed Bifurcation Theory, Archives for Rational Mechanics and Analysis, Vol. 50, pp. 159–175, 1973.

    Google Scholar 

  3. Keener, J. P., and Keller, H. B., Positive Solutions of Convex Nonlinear Eigenvalue Problems, Journal of Differential Equations, Vol. 16, pp. 103–125, 1947.

    Google Scholar 

  4. Keller, H. B., Numerical Solution of Bifurcation and Nonlinear Eigenvalue Problems, Applications of Bifurcation Theory, Edited by P. Rabinowitz, Academic Press, New York, New York, pp. 359–384, 1977.

    Google Scholar 

  5. Decker, D. W., and Keller, H. B., Multiple Limit Point Bifurcation, Journal of Mathematical Analysis and Applications, Vol. 75, pp. 417–430, 1980.

    Google Scholar 

  6. Chan, T. F., and Keller, H. B., Arclength Continuation and Multigrid Techniques for Nonlinear Eigenvalue Problems, SIAM Journal on Scientific and Statistical Computing, Vol. 3, pp. 173–194, 1982.

    Google Scholar 

  7. Keller, H. B., Practical Procedures in Path Following Near Limit Points, Computing Methods in Applied Science and Engineering, Edited by R. Glowinski and J. L. Lions, North-Holland, Amsterdam, Netherlands, Vol. 5, pp. 177–183, 1982.

    Google Scholar 

  8. Glowinski, R., Keller, H. B., and Reinhart, L., Continuation-Conjugate Gradient Methods for the Least Squares Solution of Nonlinear Boundary-Value Problems, SIAM Journal on Scientific and Statistical Computing, Vol. 6, pp. 793–832, 1985.

    Google Scholar 

  9. Bebernes, J., and Eberly, D., Mathematical Problems from Combustion Theory, Springer Verlag, New York, New York, 1989.

    Google Scholar 

  10. Carthel, C., Glowinski, R., and Lions, J. L., On Exact and Approximate Boundary Controllabilities for the Heat Equation: A Numerical Approach, Journal of Optimization Theory and Applications, Vol. 82, pp. 429–484, 1994.

    Google Scholar 

  11. Samarskii, A. A., Galaktionov, V. A., Kurdyumov, S. P., and Mikhailov, A. P., Blow-Up in Quasilinear Parabolic Equations, Walter de Gruyter, Berlin, Germany, 1995.

    Google Scholar 

  12. Glowinski, R., and Lions, J. L., Exact and Approximate Controllability for Distributed-Parameter Systems, Part 2, Acta Numerica, pp. 159–333, 1995.

  13. NeittaanmÄki, P., and Tiba, D., Optimal Control of Nonlinear Parabolic Systems: Theory, Algorithms, and Applications, Marcel Dekker, New York, New York, 1994.

    Google Scholar 

  14. Lions, J. L., Optimal Control of Systems Governed by Partial Differential Equations, Springer Verlag, New York, New York, 1971.

    Google Scholar 

  15. Glowinski, R., Numerical Methods for Nonlinear Variational Problems, Springer Verlag, New York, New York, 1984.

    Google Scholar 

  16. Daniel, J., The Approximate Minimization of Functionals, Prentice-Hall, Englewood Cliffs, New Jersey, 1970.

    Google Scholar 

  17. Berggren, M., Optimal Control of Time Evolution Systems: Controllability Investigations and Numerical Algorithms, PhD Dissertation, Department of Computational and Applied Mathematics, Rice University, 1995.

  18. Griewank, A., Achieving Logarithmic Growth of Temporal and Spatial Complexity in Reverse Automatic Differentiation, Optimization Methods and Software, Vol. 1, pp. 35–54, 1992.

    Google Scholar 

  19. Lions, J. L., Very Rapid Oscillations and Control, Proceedings of the 3rd Hellenic-European Conference on Mathematics and Informatics, Hermes 96, Athens, Greece, pp. 1–10, 1996.

  20. Barck-Holst, S., On the Numerical Simulation and Control of Systems Modeled by Partial Differential Equations, MS Thesis, Department of Mathematics, University of Houston, 1996.

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, University of Houston, Houston, Texas

    J. W. He (Visiting Assistant Professor)

  2. Department of Mathematics, University of Houston, Houston, Texas

    R. Glowinski (Professor of Mathematics)

Authors
  1. J. W. He
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. Glowinski
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

He, J.W., Glowinski, R. Neumann Control of Unstable Parabolic Systems: Numerical Approach. Journal of Optimization Theory and Applications 96, 1–55 (1998). https://doi.org/10.1023/A:1022606915736

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1022606915736

Search

Navigation