Three-Dimensional p–q Resonant Orbits Close to Second Species Solutions

Abstract

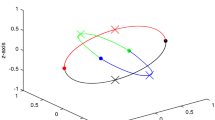
The purpose of this paper is to study, for small values of μ, the three-dimensional p–q resonant orbits that are close to periodic second species solutions (SSS) of the restricted three-body problem. The work is based on an analytic study of the in- and out-maps. These maps are associated to follow, under the flow of the problem, initial conditions on a sphere of radius μ^α around the small primary, and consider the images of those initial points on the same sphere. The out-map is associated to follow the flow forward in time and the in-map backwards. For both mappings we give analytical expressions in powers of the mass parameter. Once these expressions are obtained, we proceed to the study of the matching equations between both, obtaining initial conditions of orbits that will be 'periodic' with an error of the order μ^1−α, for some α∈(1/3,1/2). Since, as μ → 0, the inner solution and the outer solution will collide with the small primary, these orbits will be close to SSS.