Transition to Chaos and Flow Dynamics of Thermochemical Porous Medium Convection

Abstract

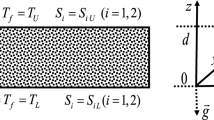
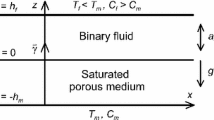
In a fluid-saturated porous medium, dissolved species advect at the pore velocity, while thermal retardation causes heat to move at the Darcy velocity. The Darcy model with the Boussinesq approximation in a square medium with a porosity of φ = 0.01 subject to two sources of buoyancy is used, to study numerically the dynamics of this so-called double-advective instability. The vertical walls of the medium are impermeable and adiabatic, while Dirichlet boundary conditions are imposed on the horizontal walls such that the medium is heated and salted from below. For an increasing ratio between chemical and thermal buoyancy, while keeping the thermal buoyancy fixed, a transition from a steady to a chaotic convective solution is observed. At the transition a stable limit cycle is found, suggesting that the transition takes the form of a Hopf bifurcation. The dynamics of the chaotic flow is characterized by irregular transitions between nonlayered and layered flow patterns, as a result of the spontaneous formation and disappearance of gravitationally stable interfaces. These interfaces temporarily divide the domain in layers of distinct solute concentration and lead to a significant reduction of kinetic energy and vertical heat and solute fluxes. The stability of an interface is described by a balance between the viscous drag forces in the convective layers and the buoyancy force associated with the density interface.