Skip to main content
SpringerLink
Log in

Study on Exact Analytical Solutions for Two Systems of Nonlinear Evolution Equations

  • Published:
Applied Mathematics and Mechanics Aims and scope Submit manuscript

Abstract

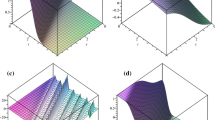
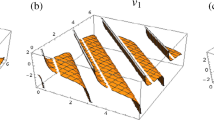
The homogeneous balance method was improved and applied to two systems of nonlinear evolution equations. As a result, several families of exact analytic solutions are derived by some new ansatzs. These solutions contain Wang's and Zhang's results and other new types of analytical solutions, such as rational fraction solutions and periodic solutions. The way can also be applied to solve more nonlinear partial differential equations.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Ablowitz M J, Clarkson P A. Solitons, Nonlinear Evolution Equations and Inverse Scattering[M]. Cambridge: Cambridge University Press,1991.

    Google Scholar 

  2. Gu C H, Li Y S. Tian C, et al. Solitons Theory and Its Applications[M]. Berlin: Springer-Verlag,1995.

    Google Scholar 

  3. GUO Bo-ling, PANG Xiao-feng. Solitons[M]. Beijing: Science Press, 1987. (in Chinese)

    Google Scholar 

  4. Wang M L, Zhou Y B, Li Z B. Application of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics[J]. Phys Lett A,1996,216(1):67–75.

    Google Scholar 

  5. Whitham G M. Variational methods and applications to water wave[J]. Proc Roy Soc London Ser A,1967,299(1):6–25.

    Google Scholar 

  6. Broer L J. Approximate equations for long water waves[J]. Appl Sci Res,1975,31(5):377–395.

    Google Scholar 

  7. Kupershmidt B A. Mathematics of dispersive water waves[J]. Comm Math Phys,1985,99(1): 51–73.

    Google Scholar 

  8. Ruan H Y, Lou S Y. Similarity analysis and Painleve property of the Kupershmidt equation[J]. Comm Theoret Phys,1993,20(1):73–80.

    Google Scholar 

  9. YAN Zhen-ya, ZHANG Hong-qing. Explicit and exact solutions for nonlinear approximate equations with long wave in shallow water [J]. Acta Phys Sinica, 1999,48(11):1962–1967. (in Chinese)

    Google Scholar 

  10. ZHANG Jie-fang. Multiple soliton solutions for the approximate equations of long water wave [J]. Acta Phys Sinica, 1998,47(9):1416–1421. (in Chinese)

    Google Scholar 

  11. ZHANG Jie-fang. Multiple solitons-like solutions for (2 + 1)-dimensional dispersive long wave equations[J]. Intern J Theoret Phys,1998,37(9):2449–2455.

    Google Scholar 

  12. Sach R L. On the integrable variant of the Boussinesq system, Painleve property, rational solutions, a related many body system, and equivalence with the AKNS hierarchy[J]. Physica D, 1988,30(1):1–27.

    Google Scholar 

  13. FAN En-gui, ZHANG Hong-qing. Backlund transformation and exact solutions for WBK equations in shallow water [J]. Applied Mathematics and Mechanics (English Edition), 1998,19(8): 713–716.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Applied Mathematics, Dalian University of Technology, Dalian, 116024, P R China

    Zhen-ya Yan & Hong-qing Zhang

Authors
  1. Zhen-ya Yan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hong-qing Zhang
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yan, Zy., Zhang, Hq. Study on Exact Analytical Solutions for Two Systems of Nonlinear Evolution Equations. Applied Mathematics and Mechanics 22, 925–934 (2001). https://doi.org/10.1023/A:1016394310716

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1016394310716

Search

Navigation