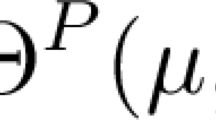Skip to main content
SpringerLink
Log in

Moduli Spaces of Maslov Complex Germs

  • Published:
Mathematical Notes Aims and scope Submit manuscript

Abstract

Maslov complex germs (complex vector bundles, satisfying certain additional conditions, over isotropic submanifolds of the phase space) are one of the central objects in the theory of semiclassical quantization. To these bundles one assigns spectral series (quasimodes) of partial differential operators. We describe the moduli spaces of Maslov complex germs over a point and a closed trajectory and find the moduli of complex germs generated by a given symplectic connection over an invariant torus.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

REFERENCES

  1. V. P. Maslov, The Complex WKB Method for Nonlinear Equations [in Russian], Nauka, Moscow, 1977.

    Google Scholar 

  2. V. P. Maslov and O. Yu. Shvedov, The Complex Germ Method in the Many-Particle Problem and in Quantum Field Theory [in Russian], URSS, Moscow, 2000.

    Google Scholar 

  3. V. M. Babich, “Eigenfunctions which are concentrated in the neighborhood of a closed geodesic,” Zap. Nauch. Sem. LOMI, 9 (1968), 15–63.

    Google Scholar 

  4. V. V. Belov and S. Yu. Dobrokhotov, “The Maslov canonical operator on isotropic manifolds with a complex germ and its applications to spectral problems,” Dokl. Akad. Nauk SSSR [Soviet Math. Dokl.], 299 (1988), no. 5, 1037–1042.

    Google Scholar 

  5. V. V. Belov and S. Yu. Dobrokhotov, “Semiclassical Maslov asymptotics with complex phases. I. General approach,” Teoret. Mat. Fiz. [Theoret. and Math. Phys.], 92 (1992), no. 2, 215–254.

    Google Scholar 

  6. V. V. Belov, O. S. Dobrokhotov, and S. Yu. Dobrokhotov, “Isotropic tori, Maslov's complex germ and index, normal forms, and quasimodes in multidimensional spectral problems,” Mat. Zametki [Math. Notes], 69 (2001), no. 4, 483–514.

    Google Scholar 

  7. Yu. M. Vorob?ev, “The complex Maslov germ generated by a linear connection,” Mat. Zametki [Math. Notes], 48 (1990), no. 6, 29–37.

    Google Scholar 

  8. Yu. M. Vorob?ev, “Quantization of isotropic tori in some nonintegrable cases,” Uspekhi Mat. Nauk [Russian Math. Surveys], 45 (1990), no. 4, 127.

    Google Scholar 

  9. Yu. M. Vorob?ev and V. A. Itskov, “Quasimodes that correspond to conditionally periodic motion of stable type,” Mat. Zametki [Math. Notes], 55 (1994), no. 5, 36–42.

    Google Scholar 

  10. S. Yu. Dobrokhotov and V. Martinez-Olive, “Closed trajectories and two-dimensional tori in a quantum spectral problem for a three-dimensional anharmonic oscillator,” Trudy Moskov. Mat. Obshch. [Trans. Moscow Math. Soc.], 58 (1997), 4–87.

    Google Scholar 

  11. S. Yu. Dobrokhotov, V. Martinez-Olive, and A. I. Shafarevich, “Closed trajectories and two-dimensional tori in the quantum Kepler problem with variable anisotropy,” Dokl. Ross. Akad. Nauk [Russian Acad. Sci. Dokl. Math.], 355 (1997), no. 3, 299–302.

    Google Scholar 

  12. A. D. Krakhnov, “Asymptotic behavior of the eigenvalues of pseudodifferential operators and invariant tori,” Uspekhi Mat. Nauk [Russian Math. Surveys], 31 (1976), no. 3, 66–74.

    Google Scholar 

  13. Topological Methods in the Theory of Hamiltonian Systems (A. B. Bolsinov, A. T. Fomenko, A. I. Shafarevich, editors) [in Russian], Faktorial, Moscow, 1998.

    Google Scholar 

  14. S. Yu. Dobrokhotov, V. Martinez-Olive, and A. I. Shafarevich, “Closed trajectories and two-dimensional tori in the quantum problem for a three-dimensional resonant anharmonic oscillator,” Russ. J. Math. Phys., 3 (1995), no. 1, 133–138.

    Google Scholar 

  15. S. Yu. Dobrokhotov and A. I. Shafarevich, “Quantum selection in semi-classical approximation of isotropic tori in partially integrable Hamiltonian systems,” Russ. J. Math. Phys., 5 (1998), no. 2, 267–272.

    Google Scholar 

  16. J. T. Duistermaat and V. W. Guillemin, “The spectrum of positive operators and periodic bicharacteristics,” Inventiones Math., 29 (1975), 39–79.

    Google Scholar 

  17. V. W. Guillemin and A. Weinstein, “Eigenvalues associated with geodesics,” Bull. Amer. Math. Soc., 82 (1976), no. 1, 92–94.

    Google Scholar 

  18. M. V. Karasev and Yu. M. Vorobjev, Integral Representation over Isotropic Submanifolds and Equations of Zero Curvature, Preprint MIEM, 1992.

  19. J. V. Ralston, “On the construction of quasimodes associated with stable periodic orbits,” Comm. Math. Phys., 51 (1976), 219–242.

    Google Scholar 

  20. A. Voros, “The WKB-Maslov method for non-separable systems,” in Géométrie symplectique et physique mathématique (Colloq. Internat. CNRS, no. 237, Aix-en-Provence, 1974), Éditions du CNRS, Paris, 1975, pp. 277–287.

    Google Scholar 

  21. S. Yu. Dobrokhotov, B. Valino-Alonso, and N. N. Nekhoroshev, “A complex germ in systems with one cyclic variable,” Uspekhi Mat. Nauk [Russian Math. Surveys], 39 (1984), no. 3, 233–234.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. M. V. Lomonosov Moscow State University, Russia

    S. E. Roganova

Authors
  1. S. E. Roganova
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Roganova, S.E. Moduli Spaces of Maslov Complex Germs. Mathematical Notes 71, 684–691 (2002). https://doi.org/10.1023/A:1015844106564

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1015844106564

Search

Navigation