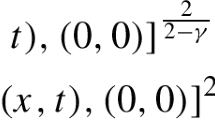Abstract
We present the foundations of the method of fundamental solutions in the mechanics of thin-walled structures and consider basic procedures of modeling that enable one to reduce mechanical problems to systems of partial differential equations with Dirac δ-functions on the right-hand sides. A method used for the construction of fundamental solutions is described. As examples, we consider the problem of action of point heat sources in a spherical orthotropic shell and the force problem for orthotropic shells with holes. The results of numerical calculations are presented in the form of plots.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
O. M. Guz' (editor), Mechanics of Composites, Vol. 7, O. M. Guz', S. Kosmodamianskii, and V. P. Shevchenko (editors), Stress Concentration [in Russian], A. S. K., Kiev (1998).
V. A. Lazaryan and S. I. Konashenko, Generalized Functions in Problems of Mechanics [in Russian], Naukova Dumka, Kiev (1974).
Ya. S. Pidstryhach and S. Ya. Yarema, Thermal Stresses in Shells [in Ukrainian], Izd. Akad. Nauk Ukr. SSR, Kiev (1961).
Generalized Functions in Thermoelasticity. A Collection of Scientific Works [in Russian], Naukova Dumka, Kiev (1980).
V. S. Vladimirov, Generalized Functions in Mathematical Physics [in Russian], Nauka, Moscow (1976).
G. N. Chernyshev, “Asymptotic methods in the theory of shells (concentrated loads),” in: Proceedings of the Sixth AllUnion Conf. on the Theory of Shells and Plates [in Russian], Nauka, Moscow (1966), pp. 883–894.
V. K. Khizhnyak and V. P. Shevchenko, Mixed Problems in the Theory of Plates and Shells [in Russian], Donetsk University, Donetsk (1980).
A. F. Nikiforov and V. B. Uvarov, Special Functions of Mathematical Physics [in Russian], Nauka, Moscow (1984).
S. Ya. Yarema, “Solution of a temperature problem for a gently sloping spherical shell in the case of concentrated heating,” in: Scientific Papers of the Institute of Machine Science and Automatics, Ser. Machine Science [in Russian], Issue 10, Izd. Akad. Nauk Ukr. SSR, Kiev (1964), pp. 80–89.
S. Ya. Yarema, “Fundamental solution of heatconduction equations for plates and gently sloping shells with internal heat sources,” Dop. Akad. Nauk Ukr. RSR. Ser. A, No. 3, 245–249 (1967).
Ya. S. Pidstryhach and Yu. M. Kolyano, Generalized Thermomechanics [in Russian], Naukova Dumka, Kiev (1976).
R. M. Shvets' and E. I. Lun', “Some problems of the theory of thermoelasticity of orthotropic shells with regard for the inertia of rotation and transverse shear,” Prikl. Mekh., 7, No. 10, 121–125 (1971).
S. A. Ambartsumyan, General Theory of Anisotropic Shells [in Russian], Nauka, Moscow (1974).
A. S. Kosmodamianskii and S. A. Kaloerov, Temperature Stresses in Multiply Connected Plates [in Russian], Vyshcha Shkola, Kiev-Donetsk (1983).
H. M. Savin, Distribution of Stresses Near Holes [in Russian], Naukova Dumka, Kiev (1968).
E. M. Dovbnya, “Investigation of the stressstrain state of an orthotropic shell with elliptic hole,” Teor. Prikl. Mekh., Issue 32, 140–144 (2001).
E. M. Dovbnya, “System of boundary integral equations for orthotropic shells of positive curvature with cuts and holes,” Teor. Prikl. Mekh., Issue 26, 59–69 (1997).
E. M. Dovbnya, “Numerical solution of a system of boundary integral equations with logarithmic singularity in problems of the theory of shells with holes,” Dinam. Sist., 15, 122–127 (1999).
E. K. Ashkenazi and É. V. Ganov, Anisotropy of Structural Materials. A Handbook [in Russian], Mashinostroenie, Leningrad (1980).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Shevchenko, V.P., Hol'tsev, A.S. & Dovbnya, E.M. Methods of Fundamental Solutions in the Mechanics of Thin-Walled Structures. Materials Science 37, 383–391 (2001). https://doi.org/10.1023/A:1013297719934
Issue Date:
DOI: https://doi.org/10.1023/A:1013297719934