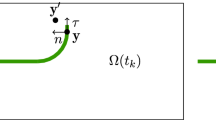
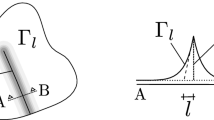
Abstract
On the basis of asymptotic formulas for the stress intensity factors and strain energy and the variational formulations of the Griffith and Irwin criteria, we propose asymptotic models of quasistatic crack growth. Under certain conditions, the transition to asymptotic models violates the equivalence of these criteria typical of the complete variational formulations. This phenomenon is analyzed and explained for a specific problem of asymmetric growth of a rectilinear crack in the elastic plane used as an example.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
REFERENCES
S. Nemat-Nasser, Y. Sumi, and L. M. Keer, “Unstable growth of tension cracks in brittle solids: stable and unstable bifurcations, snap-through and imperfection sensitivity,” Int. J. Solids Struct., 16, No. 11, 1017–1035 (1980).
S. Nemat-Nasser, “Variational methods for the analysis of stability of interacting cracks,” in: Proc. of the Third AS CE/EMD Speciality Conf., Pergamon Press, New York (1978), pp. 17–27.
V. Z. Parton and E. M. Morozov, Mechanics of Elastoplastic Fracture [in Russian], Nauka, Moscow (1974).
S. A. Nazarov, “Variational inequality for the shape of a small increment of a mode I crack,” Mekh. Tverd. Tela, No. 2, 152–160 (1989).
L. G. Kolton, “Slow growth of a system of cracks,” Mekh. Tverd. Tela, No. 5, 95–100 (1989).
S. A. Nazarov and O. R. Poyakova, “On the equivalence of fracture criteria for a mode I crack in the elastic space,” Mekh. Tverd. Tela, No. 2, 101–113 (1992).
S. A. Nazarov, “Interaction of cracks in the process of brittle fracture. Force and energy approaches,” Prikl. Mat.. Mekh., 64, No. 3, 489–501 (2000).
S. A. Nazarov and O. R. Poyakova, “Fracture criteria, asymptotic conditions at the crack tips, and self-adjoint extensions of Lamé operators,” Trudy Mosk. Math. Obshch., 56, 16–75 (1996).
G. R. Irwin, “Analysis of stresses and strains near the end of a crack traversing a plate,” Trans. ASME, J. Appl. Mech., 24, No. 3, 361–364 (1957).
A. A. Griffith, “The phenomena of rupture and flow in solids,” Philos. Trans. Roy. Soc. London, Ser. A, 221, 163–198 (1921).
L. I. Sedov, Mechanics of Continua [in Russian], Vol. 2, Nauka, Moscow (1976).
R. Glowinski, J.-L. Lions, and R. Trémoliéres, Numerical Analysis of Variational Inequalities [in French], DUNOD, Paris (1976).
D. Kinderlehrer and G. Stampacchia, An Introduction to Variational Inequalities and Their Applications, Academic Press, New York, etc. (1980).
S. A. Nazarov, “Crack on the joint of anisotropic bodies. Singularities of stresses and invariant integrals,” Prikl. Math. Mekh., 62, No. 3, 489–502 (1998).
S. A. Nazarov, “Local stability and instability of mode I cracks,” Mekh. Tverd. Tela, No. 3, 124–129 (1988).
H. F. Bueckner, “A novel principle for computation of stress intensity factor,” Z. Angew. Math. Mech., 50, 529–546 (1970).
B. T. Polyak, An Introduction to Optimization [in Russian], Nauka, Moscow (1983).
K. F. Chernykh, An Introduction to the Physically and Geometrically Nonlinear Theory of Cracks [in Russian], Nauka, Moscow (1996).
Rights and permissions
About this article
Cite this article
Argatov, I.I., Nazarov, S.A. Comparison of the Griffith and Irwin Criteria for a Crack Asymmetrically Propagating in the Plane. Materials Science 36, 561–569 (2000). https://doi.org/10.1023/A:1011370307030
Issue Date:
DOI: https://doi.org/10.1023/A:1011370307030