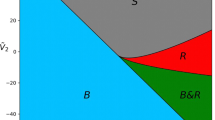
Abstract
The existence of escape and nonescape orbits arbitrarily close to the homothetic equilateral triple‐collision orbit is considered analytically in the three‐body problem with zero initial velocities and equal masses. It is proved that escape orbits in the initial condition space are distributed around three kinds of isosceles orbits. It is also proved that nonescape orbits are distributed in between the escape orbits where different particles escape. In order to show this, it is proved that the homothetic‐equilateral orbit is isolated from other triple‐collision orbits as far as the collision at the first triple encounter is concerned. Moreover, the escape criterion is formulated in the planar‐isosceles problem and translated into the words of regularizing variables. The result obtained by us explains the orbital structure numerically.
Similar content being viewed by others
References
Aarseth, S. J. and Zare, K.: 1974, ‘A regularization of the three-body problem’, Celest. Mech. 10, 185-205.
Agekian, T. A. and Anosova, J. P.: 1968, ‘A study of the dynamics of triple systems by means of statistical sampling’, Soviet Phys. Astron. 11, 1006-1014.
Anosova, J. P. and Zavalov, N. N.: 1989, ‘States of strong gravitational interaction in the general three-body problem’, Soviet Astron. 33, 79-83.
Broucke, R. A.: 1995, ‘On the role of the moment of inertia in three-body scattering’, In: A. Roy and B. Steves (eds), From Newton to Chaos, Plenum Press, New York, pp. 327-341.
Bulirsch, R. and Stoer, J.: 1966, ‘Numerical treatment of ordinary differential equations by extrapolation methods’, Numer. Math. 8, 1-13.
Devaney, R. L.: 1979, ‘Structural stability of homothetic solutions of the collinear n-body problem’, Celest. Mech. 19, 391-404.
Devaney, R. L.: 1980, ‘Triple collision in the planar isosceles three-body problem’, Inven. Math. 60, 249-267.
Laskar, J. and Marchal, C.: 1984, ‘Triple close approach in the three-body problem: a limit for the bounded orbits’, Celest. Mech. 32, 15-28.
McGehee, R.: 1974, ‘Triple collision in the collinear three-body problem’, Inven. Math. 27, 191-227.
Moeckel, R.: 1983, ‘Orbits near triple collision in the three-body problem’, Indiana Univ. Math. J. 32, 221-240.
Robinson, C.: 1984, ‘Homoclinic orbits and oscillation for the planar three-body problem’, J. Diff. Eq. 52(3), 356-377.
Simó, C.: 1980, ‘Analysis of triple collision in the isosceles problem’, In: R. L. Devaney and Z. H. Nitecki (eds), Classical Mechanics and Dynamical Systems, Marcel Dekker, New York, pp. 203-224.
Simó, C. and Martínez, R.: 1988, ‘Qualitative study of the planar isosceles three-body problem’, Celest. Mech. Dyn. Astron. 41, 179-251.
Simó, C. and Susín, A.: 1989, ‘Connections between critical points in the collision manifold of the planar 3-body problem’, In: T. Ratiu (ed.), The Geometry of Hamiltonian Systems, Springer-Verlag, pp. 497-518.
Standish, E. M.: 1971, ‘Sufficient conditions for escape in the three-body problem’, Celest. Mech. 4, 44-48.
Susín, A. and Simó, C.: 1991, Equilibrium connections on the triple collision manifold' In: A. E. Roy (ed.), Predictability, Stability, and Chaos in N-Body Dynamical Systems, Plenum Press, New York, pp. 481-512.
Tanikawa, K., Umehara, H. and Abe, H.: 1995, A search for collision orbits in the free-fall three-body problem: I. Numerical procedure' Celest. Mech. Dyn. Astron. 62, 335-362.
Tanikawa, K. and Umehara, H.: 1998, ‘Oscillatory orbits in the planar three-body problem with equal masses’, Celest. Mech. Dyn. Astron. 70, 167-180.
Umehara, H.: 1997, The free-fall three-body problem: escape and collision, PhD Thesis, The Graduate University for Advanced Studies, Mitaka, Tokyo, 181-8588 Japan.
Umehara, H., Tanikawa, K. and Aizawa, Y.: 1995, ‘Triple collision and escape in the three-body problem’, In: Y. Aizawa, S. Saito and K. Shiraiwa (eds), Dynamical Systems and Chaos, World Scientific, Singapore, Vol. 2, pp. 404-407.
Umehara, H. and Tanikawa, K.: 1996, ‘Dominant roles of binary and triple collisions in the free-fall three-body problem’, In: J. C. Muzzio, S. Ferraz-Mello and J. Henrard (eds), Chaos in Gravitational N-Body Systems, Kluwer Academic Publishers, The Netherlands, pp. 285-290.
Van Kampen, E. R. and Wintner, A.: 1937, ‘On a symmetrical canonical reduction of the problem of three bodies’, Am. J. Math. 59, 153-166.
Waldvogel, J.: 1982, ‘Symmetric and regularized coordinates on the plane triple collision manifold’, Celest. Mech. 28, 69-82.
Yoshida, J.: 1972, ‘Improved criteria for hyperbolic-elliptic motion in the general three-body problem’, Publ. Astron. Soc. Japan 24, 391-408.
Yoshida, J.: 1974, ‘Improved criteria for hyperbolic-elliptic motion in the general three-body problem. II’, Publ. Astron. Soc. Japan 26, 367-377.
Zare, K. and Szebehely, V.: 1995, ‘Order out of chaos in the three-body problem: regions of escape’, In: A. Roy and B. Steves (eds), From Newton to Chaos, Plenum Press, New York, pp. 299-313.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Umehara, H., Tanikawa, K. Orbital Distribution Arbitrarily Close to the Homothetic Equilateral Triple Collision in the Free‐Fall Three‐Body Problem with Equal Masses. Celestial Mechanics and Dynamical Astronomy 74, 69–94 (1999). https://doi.org/10.1023/A:1008397407444
Issue Date:
DOI: https://doi.org/10.1023/A:1008397407444