Skip to main content
SpringerLink
Log in

Cavitation Instabilities in Plastics and Rubber-Modified Plastics

  • Published:
International Journal of Fracture Aims and scope Submit manuscript

Abstract

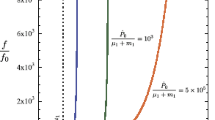
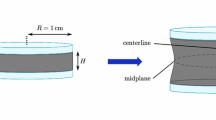
Spherical void expansion in plastics and rubber-modified plastics is investigated under radial traction conditions. The plastics are modeled as elastic-plastic pressure-sensitive materials and the rubbers are modeled as nonlinearly elastic materials. First, the growth of a spherical void in an infinite plastic matrix is investigated under remote radial traction conditions. The results show that the cavitation stress of the plastic decreases significantly as the pressure sensitivity increases. Then, the growth of a spherical void located at the center of a spherical rubber particle in an infinite plastic matrix is investigated under remote radial traction conditions. The results indicate that without any failure criteria for the rubber, the cavitation stress does not exist when the void is small and the rubber is characterized by high-order strain energy functions. However, when a failure criterion for the rubber is considered at a finite stretch ratio, the results show that the cavitation stress for the plastic with the rubber particle becomes close to that for the plastic without the rubber particle.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • Ashby, M.F., Blunt, F.J. and Bannister, M. (1989). Flow characteristics of highly constrained metal wires. Acta Metallurgica 37, 1847–1857.

    Article  Google Scholar 

  • Ball, J.M. (1982). Discontinuous equilibrium solutions and cavitation in nonlinear elasticity. Philosophical Transactions of the Royal Society of London A306, 557–611.

    ADS  Google Scholar 

  • Budiansky, B. (1959). A reassessment of deformation theories of plasticity. Transactions of the American Society of Mechanical Engineers 81E, 259–264.

    MathSciNet  Google Scholar 

  • Chang, W.J. and Pan, J. (1998). Cavitation instability in rubber with consideration of failure submitted for publication in Mathematics and Mechanics of Solids.

  • Drucker, D.C. (1973). Plasticity theory, strength-differential (SD) phenomenon, and volume expansion in metals and plastics. Metallurgical Transactions 4, 667–673.

    ADS  Google Scholar 

  • Drucker, D.C. and Prager, W. (1952). Soil mechanics and plastic analysis or limit design. Quarterly of Applied Mathematics 10, 157–165.

    MATH  MathSciNet  Google Scholar 

  • Gent, A.N. and Lindley, P.B. (1959). Internal rupture of bonded rubber cylinders in tension. Proceedings of the Royal Society of London A249, 195–205.

    ADS  Google Scholar 

  • Gent, A.N. and Wang, C. (1991). Fracture mechanics and cavitation in rubber-like solids. Journal of Materials Science 26, 339–3395.

    Google Scholar 

  • Goldberg, W. (1967). An experimental investigation of non-linear isothermal viscoelasticity, Ph.D. Thesis, Purdue University.

  • Gurson, A.L. (1975). Plastic flow and fracture behavior of ductile materials incorporating void nucleation, growth and interaction. Ph.D. Thesis, Brown University.

  • Hill, R. (1950). The Mathematical Theory of Plasticity, Clarendon Press, Oxford.

    MATH  Google Scholar 

  • Horgan, C.O. and Abeyaratne, R. (1986). A bifurcation problem for a compressible non-linearly elastic medium: growth of a micro-void. Journal of Elasticity 16, 189–200.

    Article  MATH  MathSciNet  Google Scholar 

  • Horgan, C.O. and Polignone, D.A. (1995). Cavitation in nonlinearly elastic solids: A review. Applied Mechanics Reviews 48, 471–485.

    Article  Google Scholar 

  • Hou, H. and Abeyaratne, R. (1992). Cavitation in elastic and elastic-plastic solids. Journal of the Mechanics and Physics of Solids 40, 571–592.

    Article  MATH  MathSciNet  ADS  Google Scholar 

  • Huang, Y., Hutchinson, J.W. and Tvergaard, V. (1991). Cavitation instabilities in elastic-plastic solids. Journal of the Mechanics and Physics of Solids 39, 223–241.

    Article  ADS  Google Scholar 

  • James, A.G. and Green, A. (1975). Strain energy functions of rubber. II. The characterization of filled vulcanizates. Journal of Applied Polymer Science 19, 2319–2330.

    Article  Google Scholar 

  • James, A.G., Green, A. and Simpson, G.M. (1975). Strain energy functions of rubber. I. Characterization of gum vulcanizates. Journal of Applied Polymer Science 19, 2033–2058.

    Article  Google Scholar 

  • Jeong, H.-Y. and Pan, J. (1996). Crack-tip fields for porous solids with pressure-sensitive matrices and for rubbermodified epoxies. Polymer Engineering and Science 36, 2306–2319.

    Article  Google Scholar 

  • Lazzeri, A. and Bucknall, C.B. (1993). Dilatational bands in rubber-toughened polymers. Journal of Materials Science 28, 6799–6808.

    Article  ADS  Google Scholar 

  • Li, F.Z. and Pan, J. (1990a). Plane-strain crack-tip fields for pressure-sensitive dilatant materials. Journal of Applied Mechanics 57, 40–49.

    Google Scholar 

  • Li, F.Z. and Pan, J. (1990b). Plane-stress crack-tip fields for pressure-sensitive dilatant materials. Engineering Fracture Mechanics 35, 1105–1116.

    Article  Google Scholar 

  • Morman, Jr. K.N., Kao, B.G. and Nagtegaal, J.C. (1981). Finite element analysis of viscoelastic elastomeric structures vibrating about non-linear statically stressed configurations. Fourth International Conference of Vehicle Structural Mechanics, Detroit, Michigan, 83–92.

  • Needleman, A. and Tvergaard, V. (1987). An analysis of ductile rupture modes at a crack tip. Journal of the Mechanics and Physics of Solids 35, 151–183.

    Article  MATH  ADS  Google Scholar 

  • Oden, J.T. (1972). Finite Element of Nonlinear Continua, McGraw-Hill, New York.

    Google Scholar 

  • Pearson, R.A. and Yee, A.F. (1986). Toughening mechanisms in elastomer-modified epoxies, Part 2. Microscopy studies. Journal of Materials Science 21, 2457–2488.

    Article  Google Scholar 

  • Pearson, R.A. and Yee, A.F. (1991). Influence of particle size and particle size distribution on toughening mechanisms in rubber-modified epoxies. Journal of Materials Science 26, 3828–3844.

    Article  ADS  Google Scholar 

  • Rice, J.R. and Tracey, D.M. (1969). On the ductile enlargement of voids in triaxial stress fields. Journal of the Mechanics and Physics of Solids 17, 201–217.

    Article  ADS  Google Scholar 

  • Sue, H.-J. and Yee, A.F. Micromechanical modeling of crack-tip rubber particle cavitational process in polymer toughening. Polymer Engineering and Science 36, 2320–2326.

  • Timoshenko, S.P. and Goodier, J.N. (1951). Theory of ELasticity, McGraw-Hill, New York.

    MATH  Google Scholar 

  • Tvergaard, V. (1981). Influence of voids on shear band instabilities under plane strain conditions. International Journal of Fracture 17, 389–407.

    Article  Google Scholar 

  • Tvergaard, V. (1982). On localization in ductile materials containing spherical voids. International Journal of Fracture 18, 237–252.

    Google Scholar 

  • Tvergaard, V. (1990). Material failure by void growth to coalescence. Advances in Applied Mechanics 27, 83–151.

    Article  MATH  Google Scholar 

  • Tvergaard, V. and Hutchinson, J.W. (1992). The relation between crack growth resistance and fracture process parameters in elastic-plastic solids. Journal of the Mechanics and Physics of Solids 40, 1377–1397.

    Article  MATH  ADS  Google Scholar 

  • Tvergaard, V., Huang, Y. and Hutchinson, J.W. (1992). Cavitation instabilities in a power hardening elastic-plastic solid. European Journal of Mechanics, A/Solids 11, 215–231.

    Google Scholar 

  • Truesdell, C. and Noll, W. (1965). The non-linear field theories of mechanics. Encyclopedia of Physics III/3. (Edited by S. Flugge), Springer-Verlag, Berlin.

    Google Scholar 

  • Williams, M.L. and Schapery, R.A. (1965). Spherical flaw instability in hydrostatic tension. International Journal of Fracture Mechanics 1, 64–71.

    Article  Google Scholar 

  • Xia, L. and Shih, C.F. (1995a). Ductile crack growth — I. A numerical study using computational cells with microstructurally-based length scales. Journal of the Mechanics and Physics of SOlids 43, 233–259.

    Article  MATH  ADS  Google Scholar 

  • Xia, L. and Shih, C.F. (1995b). Ductile crack growth — II. void nucleation and geometry effects on macroscopic fracture behavior. Journal of the Mechanics and Physics of Solids 43, 1953–1981.

    Article  MATH  ADS  Google Scholar 

  • Xia, L., Shih, C.F. and Hutchinson, J.W. (1995). A computational approach to ductile crack growth under large scale yielding conditions. Journal of the Mechanics and Physics of Solids 43, 389–413.

    Article  MATH  ADS  Google Scholar 

  • Yee, A.F. and Pearson, R.A. (1986). Toughening mechanisms in elastomer-modified epoxies, Part 1. Mechanical studies. Journals of Materials Science 21, 2462–2474.

    Article  ADS  Google Scholar 

  • Yee, A.F., Li, D. and Li, X. (1993). The importance of constraint relief caused by rubber cavitation in the toughening of epoxy. Journal of Materials Science 28, 6392–6398.

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Mechanical Engineering and Applied Mechanics, The University of Michigan, Ann Arbor, MI, 48109

    W.J. Chang & J. Pan

Authors
  1. W.J. Chang
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. Pan
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Chang, W., Pan, J. Cavitation Instabilities in Plastics and Rubber-Modified Plastics. International Journal of Fracture 88, 61–86 (1997). https://doi.org/10.1023/A:1007446104430

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1007446104430

Search

Navigation