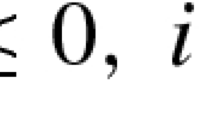Skip to main content
SpringerLink
Log in

Cutting Plane Algorithms for Nonlinear Semi-Definite Programming Problems with Applications

  • Published:
Journal of Global Optimization Aims and scope Submit manuscript

Abstract

We will propose an outer-approximation (cutting plane) method for minimizing a function f X subject to semi-definite constraints on the variables X∈R n. A number of efficient algorithms have been proposed when the objective function is linear. However, there are very few practical algorithms when the objective function is nonlinear. An algorithm to be proposed here is a kind of outer-approximation(cutting plane) method, which has been successfully applied to several low rank global optimization problems including generalized convex multiplicative programming problems and generalized linear fractional programming problems, etc. We will show that this algorithm works well when f is convex and n is relatively small. Also, we will provide the proof of its convergence under various technical assumptions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Altman, E.I. and Nelson, A.D. (1968), Financial ratios, discriminant analysis and the prediction of corporate bankruptcy. Journal of Finance 23: 589-609.

    Google Scholar 

  2. Bertsimas, D. and Popescu, I. (1998), On the relation between option and stock prices: a convex optimization approach, Technical Paper, Sloan School of Managemanet, MIT.

  3. Brace, A. and Womersley. R. S., Exact fit to the swaption volatility matrix using semidefinite programming. to appear in Mathematical Finance.

  4. Bradley, P. S., Fayyad, U. M. and Mangasarian, O. L. (1999), Mathematical programming for data mining: formulations and challenges. INFORMS J. of Computing 11: 217-238.

    Google Scholar 

  5. Fujisawa, K. Kojima, M. and Nakata, K. (1999), SDPA User's Manual-Version 5.0, Research Paper on Mathematical and Computing Science, Tokyo Institute of Technology.

  6. Gantmacher, F. R. (1959), The Theory of Matrices, Chelsea Publishing Co.

  7. Helmberg, C., Rendl, F., Vanderbei, R. J. and Wolkowitz, H. (1996), An interior point method for semi-definite programming. SIAM J. on Optimizaiton 6: 342-361.

    Google Scholar 

  8. Horst, R. and Tuy, H. (1996), Global Optimization: Deterministic Approaches, 3rd ed. Springer, Berlin.

    Google Scholar 

  9. Ioffe, A.D., and Tihomirov, V.M. (1979), Theory of External Problems. North-Holland, Amsterdam.

    Google Scholar 

  10. Kelley, J.E. (1960), The cutting-plane method for solving convex programs. J. of the Society of Industrial Applied Mathematics, 8: 703-712.

    Google Scholar 

  11. Konno, H., Gotoh, J. and Uno, T. (2000), A cutting plane algorithm for semi-definite programming problems with applications. WP 00-05, Center for Research in Advanced Financial Technology. Tokyo Institute of Technology. (to appear in J. of Computational and Applied Mathematics)

  12. Konno, H., Gotoh, J. and Uryasev, S. and Yuuki, A. (2001), Failure discrimination by semidefinite programming. WP01-02, Center for Research in Advanced Financial Technology, Tokyo Institute of Technology. (to appear in FEES 2001 (P. Pardalos, ed.))

  13. Konno, H. and Kobayashi, H. (2000), Failure discrimination and rating of enterprises by semidefinite programming, Asia-Pacific Financial Markets, 7: 261-273.

    Google Scholar 

  14. Konno, H., Thach, P.T. and Tuy, H. (1997), Optimization over Low Rank Nonconvex Structures, Kluwer Academic Publishers, Dordrecht.

    Google Scholar 

  15. Konno, H. and Wu, D. (2001), Estimation of failure probability using semi-definite logit model. WP 01-04, Center for Research in Advanced Financial Technology.

  16. Mangasarian, O., Street, W. and Wolberg, W. (1995), Breast cancer diagnoses and prognoses via linear programming. Operations Research, 43: 570-577.

    Google Scholar 

  17. Tuy, H. (1983), Outer approximation methods for solving concave minimization problems. Acta Mathematica Vietnamica, 8: 3-34.

    Google Scholar 

  18. Vandenberghe, L. and Boyd, S. (1998), Connections between semi-definite and semi-infinite programming. Semi-infinite Programming, 277-294, Kluwer Academic Publishers, Boston.

    Google Scholar 

  19. Vandenberghe, L., and Boyd, S. (1996), Semi-definite programming. SIAM Review 38: 49-95.

    Google Scholar 

  20. Veinott., A. F., Jr. (1967), The supporting hyperplane method for unimodal programming. Operations Research, 15: 147-152.

    Google Scholar 

  21. Wolkowitz, H., Saigal, R. and Vandenberghe, L. (2000), Handbook of Semi-Definite Programming: Theory, Algorithm and Application, Kluwer Academic Publishers, Dordrecht.

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Department of Industrial and Systems Engineering, Chuo-University, Japan

    Hiroshi Konno

  2. Department of Industrial Engineering and Management, Tokyo Institute of Technology, Japan

    Naoya Kawadai

  3. Institute of Mathematics, Hanoi, Vietnam

    Hoang Tuy

Authors
  1. Hiroshi Konno
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Naoya Kawadai
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Hoang Tuy
    View author publications

    You can also search for this author in PubMed Google Scholar

Rights and permissions

Reprints and permissions

About this article

Cite this article

Konno, H., Kawadai, N. & Tuy, H. Cutting Plane Algorithms for Nonlinear Semi-Definite Programming Problems with Applications. Journal of Global Optimization 25, 141–155 (2003). https://doi.org/10.1023/A:1021985014197

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1023/A:1021985014197

Search

Navigation