Skip to main content
SpringerLink
Log in

Dynamic modeling, testing, and stability analysis of an ornithoptic blimp

  • Published:
Journal of Bionic Engineering Aims and scope Submit manuscript

Abstract

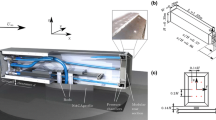
In order to study ornithopter flight and to improve a dynamic model of flapping propulsion, a series of tests are conducted on a flapping-wing blimp. The blimp is designed and constructed from mylar plastic and balsa wood as a test platform for aerodynamics and flight dynamics. The blimp, 2.3 meters long and 420 gram mass, is propelled by its flapping wings. Due to buoyancy the wings have no lift requirement so that the distinction between lift and propulsion can be analyzed in a flight platform at low flight speeds. The blimp is tested using a Vicon motion tracking system and various initial conditions are tested including accelerating flight from standstill, decelerating from an initial speed higher than its steady state, and from its steady-state speed but disturbed in pitch angle. Test results are used to estimate parameters in a coupled quasi-steady aerodynamics/Newtonian flight dynamics model. This model is then analyzed using Floquet theory to determine local dynamic modes and stability. It is concluded that the dynamic model adequately describes the vehicle’s nonlinear behavior near the steady-state velocity and that the vehicle’s linearized modes are akin to those of a fixed-wing aircraft.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

Abbreviations

φ:

Instantaneous wing heaving angle

Ch:

Amplitude of flapping oscillation

Ct:

Amplitude of wing twist at the tip

f:

Frequency of flapping

t:

Time

r:

Coordinate along span of a wing

η:

Instantaneous wing twist

φ 0 :

Phase of flapping oscillation

φ η0 :

Phase of twisting oscillation

Γ:

Circulation around the airfoil

CL:

Translational lift coefficient

CR:

Rotational lift coefficient

c(r):

Local chord value

u:

Local section velocity parallel to chord

ν:

Local section velocity normal to chord

Fν:

Viscous force

ρ:

Air density

CD(0):

Drag coefficient at zero angle of attack

CD(π/2):

Drag coefficient at 90° angle of attack

dFu:

Local force on the wing parallel to chord

dFv:

Local force on the wing normal to chord

mw:

Wing mass

α:

Angle of attack

R:

Wing length

τ:

Airfoil moment

U:

Vehicle forward velocity

W:

Vehicle velocity normal to forward velocity

Q:

Vehicle pitch rate

θ:

Vehicle pitch angle

g:

Gravitational constant

FU:

Total aerodynamic force on vehicle in forward direction

FW:

Total force on vehicle in downward normal to forward direction

m:

Vehicle mass

I y :

Moment of inertia about pitching axis

References

  1. Moon F C. The Machines of Leonardo Da Vinci and Franz Reuleaux, Springer, Dordrecht, Netherlands, 2007, 255–262.

    Book  MATH  Google Scholar 

  2. Ellington C P. The aerodynamics of hovering insect flight. I. the quasi-steady analysis. Philosophical Transactions of the Royal Society of London B, 1984, 305, 1–15.

    Article  Google Scholar 

  3. Dickinson M H, Lehmann F O, Sane S P. Wing rotation and the aerodynamic basis of insect flight. Science, 1999, 284, 1954–1960.

    Article  Google Scholar 

  4. Wang Z J. Dissecting insect flight. Annual Review of Fluid Mechanics, 2005, 37, 183–210.

    Article  MathSciNet  MATH  Google Scholar 

  5. Wang Z J. Dragonfly flight. Physics Today, 2008, 74–75.

    Google Scholar 

  6. Theodorsen T. General theory of aerodynamic instability and the mechanism of flutter. NACA Technical Report, 1935, 496.

    Google Scholar 

  7. Jones R T. The unsteady lift of a wing of finite aspect ratio. NACA Technical Report, 1940, 681.

    Google Scholar 

  8. DeLaurier J D. An aerodynamic model for flapping-wing flight. Aeronautical Journal, 1993, 97, 125–130.

    Google Scholar 

  9. Taylor G K, Bacic M, Bomphrey R J, Carruthers A C, Gillies J, Walker S M, Thomas A R L. New experimental approaches to the biology of flight control systems. Journal of Experimental Biology, 2008, 211, 258–266.

    Article  Google Scholar 

  10. Zdunich P, Bilyk D, MacMaster M, Loewen D, Delaurier J, Kornbluh R, Low T, Stanford S, Holeman D. Development and testing of the mentor flapping-wing micro air vehicle. Journal of Aircraft, 2007, 44, 1701–1711.

    Article  Google Scholar 

  11. Grauer J, Ulrich E, Hubbard J, Pines D, Humbert J S. Testing and system identification of an ornithopter in longitudinal flight. Journal of Aircraft, 2011, 48, 660–667.

    Article  Google Scholar 

  12. Krashanitsa R, Silin D, Shkarayev S, Abate G. Flight dynamics of a flapping-wing air vehicle. International Journal of Micro Air Vehicles, 2009, 1, 35–49.

    Article  Google Scholar 

  13. Dietl J M, Garcia E. Stability in ornithopter longitudinal flight dynamics. Journal of Guidance, Control, and Dynamics, 2008, 31, 1157–1162.

    Article  Google Scholar 

  14. Berman G, Wang Z J. Energy-minimizing kinematics in hovering insect flight. Journal of Fluid Mechanics, 2007, 582, 153–168.

    Article  MathSciNet  MATH  Google Scholar 

  15. Bar-Shalom Y, Li X R, Kirubarajan T. Estimation with Applications to Tracking and Navigation, John Wiley and Sons Inc., New York, USA, 2001, 138–140.

    Book  Google Scholar 

  16. Dietl J M, Garcia E. Ornithopter control with periodic infinite horizon controllers. Journal of Guidance, Control, and Dynamics, 2011, 34, 1412–1422.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Sibley School of Mechanical and Aerospace Engineering, Cornell University, Ithaca, New York, USA

    John Dietl, Thomas Herrmann & Ephrahim Garcia

  2. Air Force Research Laboratory, Wright-Patterson AFB, OH, 45433-7542, USA

    Gregory Reich

Authors
  1. John Dietl
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Thomas Herrmann
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Gregory Reich
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Ephrahim Garcia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to John Dietl.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dietl, J., Herrmann, T., Reich, G. et al. Dynamic modeling, testing, and stability analysis of an ornithoptic blimp. J Bionic Eng 8, 375–386 (2011). https://doi.org/10.1016/S1672-6529(11)60043-7

Download citation

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S1672-6529(11)60043-7

Keywords

Search

Navigation