Skip to main content
SpringerLink
Log in

Investigation on the Flow Stability of Newtonian Fluid in Eccentric Annulus Via the Axial Reciprocation of the Inner Tube

  • Published:
Journal of Hydrodynamics Aims and scope Submit manuscript

Abstract

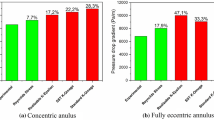
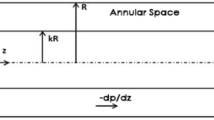
The governing equation, together with the formulas of the averaged flux and the stability parameter for Newtonian fluid flowing in eccentric annulus via the axial reciprocation of the inner tube was established in the bipolar coordinate system. Numerical calculation was conducted for the measurement of water flow using the formulas above, of which the results agree well with the experimental data. It is shown that the flow instability can be induced by the increase of the stroke, the frequency, and the eccentricity of annulus, making the sucker rod more susceptible to partial abrasion. Some protecting methods, including adding centralizers, adjusting the stroke and frequency, are proposed to protect the sucker rod from the partial abrasion, and satisfactory results have been achieved in the oilfields.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. MA Liang, NIE Jian-jun. Numerical simulation of flow field in the tube with a moving pole and hoop inside[J]. Journal of Hydrodynamics, Ser. A, 2003, 18(1): 1–7 (in Chinese).

    Google Scholar 

  2. JIA Shan-po, YAN Xiang-zhen and JIANG Shi-hu et al. Numerical simulation of low law of fluid in the barrel of sucker rod pumps[J]. China Petroleum Machinery, 2003, 31(8): 13–18 (in Chinese).

    Google Scholar 

  3. DONG Shi-min. Mechanical analysis on causes of worn rod string and tubing of rod pumping wells in the water-flooding oilfield[J]. Acta Petrolei Sinica, 2003, 24(4): 108–112 (in Chinese).

    MathSciNet  Google Scholar 

  4. HAN Hong-sheng, WANG De-min and GUO Li-ping et al. Partial abrasion mechanism of sucker rod caused by normalstress of visco-elastic fluid[J]. Acta Petrolei Sinica, 2004, 25(4): 92–95 (in Chinese).

    Google Scholar 

  5. YUE Xiang-an, CHEN Jia-lang and HUANG Kuang-dao. The analytical solution of velocity distribution for power-law fluid axial laminar flow through eccentric annuli[J]. Journal of Hydrodynamics, Ser. A, 1988, 3(3): 1–4 (in Chinese).

    MATH  Google Scholar 

  6. JIANG Shi-quan, SHI Tai-he. An analytic solution of spiral flow in an eccentric annulus [J]. Journal of Hydrodynamics, Ser. A, 1995, 10(5): 560–565 (in Chinese).

    Google Scholar 

  7. WANG Yan-hui. Turbulent property of non-Newtonian fluid in eccentric annulus[J]. Journal of Hydrodynamics, Ser. A, 1997, 12(2): 150–156 (in Chinese).

    Google Scholar 

  8. CUI Hai-qing, SUN Zhi and GAO Tao. Velocity distribution of unsteady flow of non-Newtonian fluid in eccentric annuli with the inner cylinder reciprocating axially[J]. Journal of Hydrodynamics, Ser. A, 2003, 18(6): 711–715 (in Chinese).

    Google Scholar 

  9. CUI Hai-qing, YANG Yuan-jian and GAO Tao et al. Flow rate calculation of the unsteady flow of power law fluid in eccentric annuli with the inner cylinder reciprocating axially[J]. Acta Petrolei Sinica, 2005, 26(3): 106–109 (in Chinese).

    Google Scholar 

  10. WANG Yan, CUI Hai-qing and YANG Yuan-jian et al. Pressure distribution on the wall of the inner cylinder reciprocating axially to the unsteady flow of viscoelastic fluid in eccentric annulus[J]. Journal of Hydrodynamics, Ser. B, 2006, 18(5): 606–612.

    Article  Google Scholar 

  11. BALLAL B. Y., RIVLIN R. S. Flow of a viscoelastic fluid between eccentric cylinders[J]. Rheologica Acta, 1979, 18(3): 311–322.

    Article  Google Scholar 

  12. BALLAL B. Y., RIVLIN R. S. Flow of a viscoelastic fluid between eccentric cylinders, I. Rectilinear shearing flow[J]. Rheologica Acta, 1975, 14(6): 484–492.

    Article  Google Scholar 

  13. HANKS R. W. A theory of laminar flow stability[J]. AIChE Journal, 1969, 15(1): 5–29.

    Article  MathSciNet  Google Scholar 

  14. ZHANG Jin-fu, DAI Kui. The laminar helical flow and flow stability of Herschel-Bulkelyfluid in inclined pipes [J]. Journal of Hydrodynamics, Ser. A, 2003, 18(5): 607–612 (in Chinese).

    Google Scholar 

  15. LIU Nai-zhen, WANG Ting-rui and LIU Xiao-liang. Stability of non-Newtonian fluid and its flow pattern discrimination [J]. Natural gas industry, 2003, 23(1): 53–57 (in Chinese).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Management Institute, Tianjin University, Tianjin, 300072, China

    Ai-wu Yuan

  2. Department of Petroleum Engineering, Daqing Petroleum Institute, Daqing, 163318, China

    Ai-wu Yuan & Hai-qing Cui

  3. Daqing Exploration and Development Institute, Daqing, 163712, China

    Tao Gao

Authors
  1. Ai-wu Yuan
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Hai-qing Cui
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Tao Gao
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Ai-wu Yuan.

Additional information

Project supported by the National Natural Science Foundation of China (Grand No. 50674019) and the Natural Science Foundation of Heilongjiang Province (Grant No. A200501).

Biography: YUAN Ai-wu(1974-), Female, Ph. D., Senior Engineering

Rights and permissions

Reprints and permissions

About this article

Cite this article

Yuan, Aw., Cui, Hq. & Gao, T. Investigation on the Flow Stability of Newtonian Fluid in Eccentric Annulus Via the Axial Reciprocation of the Inner Tube. J Hydrodyn 19, 671–676 (2007). https://doi.org/10.1016/S1001-6058(08)60002-5

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S1001-6058(08)60002-5

Key words

Search

Navigation