Skip to main content
SpringerLink
Log in

Guided waves in multilayered plates: An improved orthogonal polynomial approach

  • Published:
Acta Mechanica Solida Sinica Aims and scope Submit manuscript

Abstract

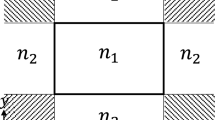
Conventional orthogonal polynomial approach can solve the multilayered plate only when the material properties of two adjacent layers do not change significantly. This paper developed an improved orthogonal polynomial approach to solve wave propagation in multilayered plates with very dissimilar material properties. Through numerical comparisons among the exact solution, the results from the conventional polynomial approach and from the improved polynomial approach, the validity of the improved polynomial approach is illustrated. Finally, it is shown that the conventional polynomial approach can not yield correct continuous normal stress profiles. The improved orthogonal polynomial approach has overcome this drawback.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Maradudin, A.A., Wallis, R.F., Mills, D.L. and Ballard, R.L., Vibrational edge modes in finite crystals. Physical Review B, 1972, 6: 1106–1111.

    Article  Google Scholar 

  2. Sharon, T.M., Maradudin, A.A. and Cunningham, S.L., Vibrational modes on a rectangular ridge. Letters in Applied and Engineering Sciences, 1974, 2: 161–174.

    Google Scholar 

  3. Maradudin, A.A. and Subbaswamy, K.R., Edge localized vibration modes on a rectangular ridge. Journal of Applied Physics, 1977, 48: 3410–3414.

    Article  Google Scholar 

  4. Datta, S. and Hunsinger, B.J., Analysis of surface waves using orthogonal functions. Journal of Applied Physics, 1978, 49: 475–479.

    Article  Google Scholar 

  5. Kim, Y. and Hunt, W.D., Acoustic fields and velocities for surface-acoustic-wave propagation in multilayered structures: An extension of the Laguerre polynomial approach. Journal of Applied Physics, 1990, 68: 4993–4997.

    Article  Google Scholar 

  6. Gubernatis, J.E. and Maradudin, A.A., A Laguerre series approach to the calculation of wave properties for surfaces of inhomogeneous elastic materials. Wave Motion, 1987, 9: 111–121.

    Article  MathSciNet  Google Scholar 

  7. Lefebvre, J.E., Zhang, V., Gazalet, J. and Gryba, T., Legendre polynomial approach for modeling free ultrasonic waves in multilayered plates. Journal of Applied Physics, 1999, 85: 3419–3427.

    Article  Google Scholar 

  8. Lefebvre, J.E., Zhang, V., Gazalet, J., Gryba, T. and Sadaune, V., Acoustic wave propagation in continuous functionally graded plates: An extension of the Legendre polynomial approach. IEEE Transactions on Ultrasonics Ferroelectrics and Frequency Control, 2001, 48: 1332–1340.

    Article  Google Scholar 

  9. Elmaimouni, L., Lefebvre, J.E., Zhang, V. and Gryba, T., Guided waves in radially graded cylinders: a polynomial approach. NDT & E International, 2005, 38: 344–353.

    Article  Google Scholar 

  10. Yu, J.G., Wu, B. and Chen, G., Wave characteristics in functionally graded piezoelectric hollow cylinders. Archive of Applied Mechanics, 2009, 79: 807–824.

    Article  Google Scholar 

  11. Yu, J.G. and Ma, Q., Circumferential wave in functionally graded piezoelectric cylindrical curved plates. Acta Mechanica, 2008, 198: 171–190.

    Article  Google Scholar 

  12. Yu, J.G., Wu, B., Huo, H. and He, C.F., Characteristics of guided waves in anisotropic spherical curved plates. Wave Motion, 2007, 44: 271–281.

    Article  Google Scholar 

  13. Yu, J.G., Wu, B. and He, C.F., Characteristics of guided waves in graded spherical curved plates. International Journal of Solids and Structures, 2007, 44: 3627–3637.

    Article  Google Scholar 

  14. Yu, J.G., Wu, B. and He, C.F., Wave propagation in non-homogeneous magneto-electro-elastic plates. Journal of Sound and Vibration, 2008, 317: 250–264.

    Article  Google Scholar 

  15. Yu, J.G. and Wu, B., Circumferential wave in magneto-electro-elastic functionally graded cylindrical curved plates. European Journal of Mechanics—A/Solids, 2009, 28: 560–568.

    Article  Google Scholar 

  16. Yu, J.G., Wu, B. and He, C.F., Guided thermoelastic wave propagation in layered plates without energy dissipation. Acta Mechanica Solida Sinica, 2011, 24(2): 135–143.

    Article  Google Scholar 

  17. Yu, J.G., Zhang, X.M. and Xue, T.L., Generalized thermoelastic waves in functionally graded plates without energy dissipation. Composite Structures, 2010, 93(1): 32–39.

    Article  Google Scholar 

  18. Yu, J.G., Wu, B. and He, C.F., Guided thermoelastic waves in functionally graded plates with two relaxation times. International Journal of Engineering Science, 2010, 48(12): 1709–1720.

    Article  Google Scholar 

  19. Yu, J.G., Viscoelastic shear horizontal wave in graded and layered plates. International Journal of Solids and Structures, 2011, 48(16–17): 2361–2372.

    Google Scholar 

  20. Yu, J.G., Ratolojanahary, F.E. and Lefebvre, J.E., Guided waves in functionally graded viscoelastic plates. Composite Structures, 2011, 93(11): 2671–2677.

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mechanical and Power Engineering, Henan Polytechnic University, 454003, Jiaozuo, China

    Jiangong Yu

  2. Univ Lille Nord de France, F-59000, Lille, France

    J. E. Lefebvre

  3. UVHC, IEMN-DOAE, Valenciennes Cedex 9, F-59313, France

    J. E. Lefebvre

  4. CNRS, UMR 8520, F-59650, Villeneuve d’Ascq, France

    J. E. Lefebvre

  5. Department of Civil Engineering, University of Siegen, D-57068, Siegen, Germany

    Jiangong Yu

  6. ERSITA, Faculté Polydisciplinaire d’Ouarzazate, Univ. Ibn Zohr, 45000, Ouarzazate, Morocco

    L. Elmaimouni

  7. LMTI, Faculté des Sciences d’Agadir, Université Ibn Zohr, BP 28/S, Agadir, Morocco

    L. Elmaimouni

Authors
  1. Jiangong Yu
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. J. E. Lefebvre
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. L. Elmaimouni
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Jiangong Yu.

Additional information

Project supported by the National Natural Science Foundation of China (No. 11272115). Jiangong Yu gratefully acknowledges the support by Alexander von Humboldt-Foundation (AvH) to conduct research work at university of Siegen, Germany.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Yu, J., Lefebvre, J.E. & Elmaimouni, L. Guided waves in multilayered plates: An improved orthogonal polynomial approach. Acta Mech. Solida Sin. 27, 542–550 (2014). https://doi.org/10.1016/S0894-9166(14)60062-8

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1016/S0894-9166(14)60062-8

Key Words

Search

Navigation