Abstract
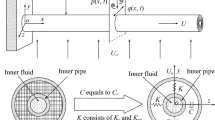
In this paper, the nonlinear dynamical behavior of two coupled pipes conveying pulsating fluid is studied. The connection between the two pipes is considered as a distributed linear spring. Based on this consideration, the equations of motion of the coupled two-pipe system are obtained. The two coupled nonlinear partial differential equations, discretized using the fourth-order Galerkin method, are solved by a fourth-order Runge-Kutta integration algorithm. Results show that the connection stiffness has a significant effect on the dynamical behavior of the coupled system. It is found that for some parameter values the motion types of the two pipes might be synchronous.
Similar content being viewed by others
References
Païoussis, M.P., Fluid-Structure Interactions: Slender Structures and Axial Flow. London: Academic Press, 1998.
Païoussis, M.P. and Issid, N.T., Dynamic stability of pipes conveying fluid. Journal of Sound and Vibration, 1974, 33: 267–294.
Chatjigeorgiou, I.K. and Mavrakos, S.A., Bounded and unbounded coupled transverse response of para-metrically excited vertical marine risers and tensioned cable legs for marine applications. Applied Ocean Research, 2002, 24: 341–354.
Chatjigeorgiou, I.K. and Mavrakos, S.A., Nonlinear resonances of parametrically excited risers—numerical and analytic investigation for Ω = 2ω1. Computers and Structures, 2005, 83: 560–573.
Yang, X.D., Yang, T.Z. and Jin, J.D., Dynamic stability of a beam-model viscoelastic pipe for conveying pulsative fluid. Acta Mechanica Solida Sinica, 2007, 20: 350–356.
Qian, Q., Wang, L. and Ni, Q., Nonlinear responses of a fluid-conveying pipe embedded in nonlinear elastic foundations. Acta Mechanica Solida Sinica, 2008, 21: 170–176.
Stangl, M., Gerstmayr, J. and Irschik, H., An alternative approach for the analysis of nonlinear vibrations of pipes conveying fluid. Journal of Sound and Vibration, 2008, 310: 493–511.
Giacobbi, D.B., Rinaldi, S., Semler, C. and Païoussis, M.P., The dynamics of a cantilevered pipe aspirating fluid studied by experimental, numerical and analytical methods. Journal of Fluids and Structures, 2012, 30: 73–96.
Wang, L., Flutter instability of supported pipes conveying fluid subjected to distributed follower forces. Acta Mechanica Solida Sinica, 2012, 25: 46–52.
Bajaj, A.K., Nonlinear dynamics of tubes carrying a pulsatile flow. Dynamics and Stability of Systems, 1987, 2: 19–41.
Namchchivaya, N.S., Non-linear dynamics of supported pipe conveying pulsating fluid—I. Subharmonic resonance. International Journal of Non-Linear Mechanics, 1989, 24: 185–196.
Namchchivaya, N.S. and Tien, W.M., Non-linear dynamics of supported pipe conveying pulsating fluid—II. Combination resonance. International Journal of Non-Linear Mechanics, 1989, 24: 197–208.
Öz, H.R., Non-linear vibrations and stability analysis of tensioned pipes conveying fluid with variable velocity. International Journal of Non-Linear Mechanics, 2001, 36: 1031–1039.
Jin, J.D. and Song, Z.Y., Parametric resonances of supported pipes conveying pulsating fluid. Journal of Fluids and Structures, 2005, 20: 763–783.
Panda, L.N. and Kar, R.C., Nonlinear dynamics of a pipe conveying pulsating fluid with parametric and internal resonances. Nonlinear Dynamics, 2007, 49: 9–30.
Panda, L.N. and Kar, R.C., Nonlinear dynamics of a pipe conveying pulsating fluid with combination, principal parametric and internal resonances. Journal of Sound and Vibration, 2008, 309: 375–406.
Wang, L., A further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid. International Journal of Non-Linear Mechanics, 2009, 44: 115–121.
Wang, L., Erratum to “a further study on the non-linear dynamics of simply supported pipes conveying pulsating fluid” [International Journal of Non-Linear Mechanics, 2009, 44: 115–121]. International Journal of Non-Linear Mechanics, 2010, 45: 331–335.
Modarres-Sadeghi, Y. and Paidoussis, M.P., Nonlinear dynamics of extensible fluid-conveying pipes, supported at both ends. Journal of Fluids and Structures, 2009, 25: 535–543.
Author information
Authors and Affiliations
Corresponding author
Additional information
Project supported by the National Natural Science Foundation of China (Nos. 11172107 and 11172109) and the Program for New Century Excellent Talents in University (No. NCET-11-0183).
Rights and permissions
About this article
Cite this article
Ni, Q., Zhang, Z., Wang, L. et al. Nonlinear Dynamics and Synchronization of Two Coupled Pipes Conveying Pulsating Fluid. Acta Mech. Solida Sin. 27, 162–171 (2014). https://doi.org/10.1016/S0894-9166(14)60026-4
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1016/S0894-9166(14)60026-4