1 Introduction

The mooring-HLC-cargo system is an important operation system in ocean engineering (He et al. 2017; Le and Lee 2017; Smoczek and Szpytko 2017). In practice, such a heavy system always generates a large amplitude of oscillation in the presence of complex sea conditions, wind, waves, ocean currents, and other interference forces. Consequently, the lifted object of the HLC has an excessive swing amplitude, which threatens the safety of the crane ship in operation (Cha et al. 2010; Ku and Ha 2014).

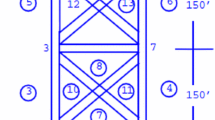
The mooring-HLC-cargo system is a complicated coupling mechanical structure system with a rigid body, elastic body, and fluid, as illustrated in Fig. 1 (Wang et al. 2024b). Moreover, a strong coupling relationship exists between the hull and wind and wave loads, mooring system, and suspended load, which increases the system model complexity when functioning in a real marine environment. Therefore, it is difficult to obtain an accurate model and design a control method to suppress the swing. To improve the swing control of the suspended object, researchers have created diverse models of the mooring-floating crane-suspended object system, and a large amount of research results have been documented in this area. Idres et al. (2012) recognized the nonlinear dynamic model of the crane ship by coupling the eight-degree-of-freedom dynamic model of the hull with the nonlinear large-angle load swing. Chilinski et al. (2020) developed a multibody motion equation signifying the physical connection of joints or wire ropes through the Lagrange method, examined the dynamics of the floating crane lifting system, and provided a group of regular waves with different wave heights, directions, and periods to replicate the dynamic response characteristics of the crane lifting system. To improve establishing the accurate model of the crane ship lifting system in the actual environment, Qian and Fang (2016) considered the influence of the wave force on the system, created the corresponding wave force model, examined the dynamic characteristics of the marine crane under certain regular wave disturbance by using the Lagrange method, and established the accurate dynamic system including the effect of the wave force.

Fig. 1
figure 1

Mooring-HLC-cargo system (Wang et al. 2024b)

Full size image

Regular and irregular waves with different water depths, wave heights, and periods always produce diverse, dynamic response characteristics of the system. Li and Lin (2012) studied the wave-body interaction of the floating body structure in a 2D wave tank; explored the relationship between the water depth, wave height, wave period, and the interaction force between the wave and the hull; and defined specific rules. Given the above analysis of the model of the mooring-HLC-cargo system and the dynamic response of the wave force to the system, the existing model of the crane lifting system does not take the influence of the wave force on the lifting system as the system interference.

Few results were developed to suppress the swing of the suspended object on the system. Zanjani and Mobayen (2021) designed a global sliding mode controller. After linearizing the crane ship lifting system, it was used in the swing suppression control problem of the crane ship lifting system. Yang et al. (2019) designed an adaptive control method based on a neural network for the crane ship system working in a complex marine environment to ensure that the system can preserve satisfactory control performance when parameters such as boom length and payload mass are modified. Considering the control input constraints, Chen et al. (2016) proposed a new model predictive control method for the problem of load swing in underactuated cranes. However, the existing antiswing control schemes for the mooring-HLC-cargo coupled system do not regard the wave force acting on the system as a disturbance that can be modeled; they use the corresponding antidisturbance control scheme to examine it and deal with it, which is of important for the suspended cargo system to consider swing suppression control and antidisturbance control problems.

When the wave force disturbance is modeled as the exosystem, the antidisturbance method can be used to deal with the influence of the wave force on the swing of the suspended object effectively, which deserves further investigation.

The modellable disturbance generated by the exosystem is a common, important type of disturbance in studying antidisturbance theory (Nikiforov 1998; Wei and Guo 2010; Yao and Guo 2013; Wei et al. 2020), and the disturbance model can describe many types of disturbances. Researchers have also conducted a large number of studies on the disturbance generated by the exosystem. Guo and Chen (2005) proposed a control method based on the disturbance observer for the modellable disturbance generated by the unknown linear exosystem, which supplies a new idea and design method for the compensation of such disturbance. Dong and Wei (2018) proposed a stochastic nonlinear disturbance observer by examining the disturbance generated by the external system with known nonlinearity and then established a disturbance attenuation control method based on the nonlinear disturbance observer. Qi et al. (2019) considered not only the nonlinearity in the exosystem but also the situation that the exosystem has unmodellable disturbances at the same time. They combined the nonlinear disturbance observer with dissipative analysis and proposed a composite antidisturbance control technique based on the nonlinear disturbance observer. However, the nonlinearity of the exosystem is not always known in the actual situation, and this area still has some theoretical research gaps. Thus, designing an effective disturbance observer and the corresponding controller to compensate for the disturbance has theoretical importance and research value.

Given the problems of nonlinear model uncertainty in modern control theory and the need to adjust system parameters in time under complex, changeable environments, researchers have proposed an adaptive fuzzy control strategy (Wang 1993; Lu 2018; Zhang et al. 2018; Sun et al. 2020) for nonlinear uncertain systems. Adaptive fuzzy control does not require an accurate system model to adjust parameters while still maintaining good stability and control effect of the system in the presence of disturbances. To make full use of this ability, numerous adaptive fuzzy control schemes based on disturbance observers have been proposed in recent years. Wang et al. (2023a) considered the complex underwater working environment of the underwater robot-manipulator system and designed the adaptive fuzzy control strategy of the underwater robot-manipulator system based on the fuzzy performance observer and disturbance observer by considering factors such as modeling uncertainty, external disturbance, and dead-zone input nonlinearity in the system model. The stability and excellent tracking performance of the system are guaranteed. Ma et al. (2023) proposed an adaptive fuzzy control scheme based on disturbance observer for the 6-degree-of-freedom unmanned helicopter with system uncertainties, flight boundary constraints, and external disturbances so that the position and pose state of the unmanned helicopter system can achieve the expected safety tracking performance. Qiu et al. (2022) studied the problem of adaptive fuzzy finite-time control based on disturbance observer for strict-feedback nonlinear systems and considered the preset performance of the system in finite time, which can ensure that the tracking error of the system converges to a prescribed bounded set in a known finite time. However, the results on adaptive fuzzy antidisturbance control for systems with nonlinear exosystems, without mentioning the unknown nonlinear exosystem, are very few.

Based on the above analysis, the design problem of an adaptive fuzzy control strategy based on fuzzy disturbance observer (FDO) is studied for the mooring-HLC-cargo coupled system with the disturbance modeled by the unknown nonlinear wave force exosystem. The adaptive fuzzy control strategy based on radial basis function (RBF) fuzzy logic system (FLS) is used to estimate internal unknown nonlinear functions and external disturbances, and an FDO is designed to approximate the external modeled disturbance generated by the nonlinear wave force exosystem. In the presence of uncertainties and disturbances, the closed-loop system is guaranteed to be bounded, the swing amplitude of the suspended object is reduced, and the required control torque is controlled within a certain range. Compared with the existing results, the contributions of this article are listed as follows.

Different from the existing mooring-HLC-cargo coupled system, the system studied in this paper considers the modellable part of the wave force and models it as an exosystem with unknown nonlinearity, which can represent a more general form of wave force disturbance.

Different from the existing linear and nonlinear disturbance observers, a new FDO is designed in combination with the RBF FLS to learn the unknown function part in the nonlinear wave force exosystem. Moreover, a new disturbance estimation error observer (DEEO) is constructed to generate the estimates of the unknown states in the premise variables.

By using FDO and DEEO, a fuzzy disturbance observer-based control (FDOBC) design method is proposed and applied to the swing suppression control problem of the mooring-HLC-cargo coupled system, which provides a new idea and scheme for solving this kind of problem.

The rest of the paper is structured as follows. In Section 2, the mooring-HLC-cargo coupled system is modeled and simplified, and the modellable wave force is considered. In Section 3, the controller design based on FDO is described in detail. In Section 4, the stability theorem of the system is presented. In Section 5, the numerical simulation results exhibit that the proposed control scheme has a satisfactory control performance. Finally, in Section 6, the work done in this paper is summarized.

2 Problem formulation and preliminaries

2.1 Defining the coordinate system

Relevant coordinate systems for different parts of the mooring-HLC-cargo coupled system are set, as presented in Fig. 2, where o-xyz is the vessel-fixed coordinate system of the HLC, o'-x'y'z' is the translational coordinate system, O-XYZ is the geodetic coordinate system, the plane \(XOY\) is located on the still water level, and the z-axis is vertical to the still water level and upward.

Fig. 2
figure 2

Sketch of an offshore HLC vessel

Full size image

OP-XPYPZP is the boom-fixed coordinate system, and the ZP-axis is vertical and downward. l is the length of the lifting rope, and G0 represents the cargo. The in-plane angle α is the angle between the ZP-axis and the lifting rope’s projection (OPG'0) on the XPOPZP plane, and the out-plane angle β is the angle between the lifting rope (OPG0) and its projection (OPG'0) on the XPOPZP plane. α, β, and l are employed to describe the motion of the cargo.

The coordinate of the boom-tip P of the HLC vessel in the geodetic coordinate system is \({\boldsymbol{x}}_{P}\) (Diebel 2006).

$${\boldsymbol{x}}_{P} = {\boldsymbol{x}}_{G} + T \cdot {\boldsymbol{x}}_{P}{'},$$
(1)

where \({\boldsymbol{x}}_{G}\) is the coordinate of the vessel’s COG in the geodetic coordinate system, T is the coordinate transformation matrix composed of Euler angles, and \({\boldsymbol{x}}_{P}{'}\) is the coordinate of the boom-tip in the vessel-fixed coordinate system.

2.2 Coupled ‘mooring-HLC-cargo’ system

According to (Zhang et al. 2022; Wang et al. 2023b), the following motion equation of the moored HLC vessel is derived:

$$\begin{gathered} \left( {{\boldsymbol{M}} + {\boldsymbol{M}}_{\infty } } \right){\boldsymbol{\ddot{x}}} + \int_{0}^{t} {{\boldsymbol{K}}_{R} } (t - \tau ){\dot{\boldsymbol{x}}}(\tau ){\text{d}}\tau + {\boldsymbol{D}}_{1} {\dot{\boldsymbol{x}}} + {\boldsymbol{K}}_{HS} {\boldsymbol{x}} \\ = {\boldsymbol{F}}_{W1} + {\boldsymbol{F}}_{W2} + {\boldsymbol{F}}_{m} + {\boldsymbol{F}}_{WD} + {\boldsymbol{F}}_{C} + {\boldsymbol{F}}_{L} \\ \end{gathered},$$
(2)

where \({\boldsymbol{x}} \in {\mathbb{R}}^{6}\) is the motion vector, M is the mass matrix, \({\boldsymbol{M}}_{\infty }\) is the additional mass at the infinite frequency, \({\boldsymbol{K}}_{R} (t - \tau )\) is the retardation function, \({\boldsymbol{D}}_{1}\) is the linear damping matrix, \({\boldsymbol{K}}_{HS}\) is the hydrostatic matrix, \({\boldsymbol{F}}_{W1}\) and \({\boldsymbol{F}}_{W2}\) are the first- and second-order wave excitation forces, respectively. \({\boldsymbol{F}}_{m}\), \({\boldsymbol{F}}_{WD}\), \({\boldsymbol{F}}_{C}\), and \({\boldsymbol{F}}_{L}\) are the mooring line forces, wind forces, current forces, and cargo forces acting on the HLC vessel, respectively.

2.3 Power compensated model of swing suppression and its working principle

Based on the new concept of HPPCD for a floating HLC (Wang et al. 2024a), a swing suppression with power compensation is developed. The simplified structure of the HPPCD of a floating HLC is shown in Fig. 3.

Fig. 3
figure 3

Simplified structure of HPPCD

Full size image

Particle Q is the fixed pulley to create a bidirectional damping force to suppress the swing of the cargo. The lifting rope is assumed to be fixed to particle Q with a local coordinate system OQ-XQYQZQ. The above plane remains parallel to the plane of the boom-fixed coordinate system OP-XPYPZP in the same direction when particle Q moves. The parameters of the simplified system are listed in Table 1.

Table 1 Parameters of the system model
Full size table

Particle Q can produce the active bidirectional resultant forces Fx and Fy to suppress the in-plane and out-of-plane angles. Fx and Fy are composed of the driving forces and the wave forces acting on the points Q as follows:

$$F_{x} = F_{ax} + F_{wx},$$
(3)
$$F_{y} = F_{ay} + F_{wy},$$
(4)

where \(F_{ax}\) and \(F_{ay}\) represent the control forces given by the controller to be designed in the control algorithm, and \(F_{wx}\) and \(F_{wy}\) represent the forces generated by the modeled wave force disturbance.

2.4 First- and second-order wave force

The generalized wave force of long-crested irregular waves acting on the structure can be written as follows (Du et al. 2019):

$$F_{j} (t) = F_{j}^{(1)} (t) + F_{j}^{(2)} (t) \, (j = 1,2, ... ,6).$$
(5)

By convolution of the impulse response function of the generalized wave force and the wave height, the first- and second-order wave exciting forces Fj(1)(t) and Fj(2)(t) are derived as follows:

$$F_{j}^{(1)} (t) = \int\limits_{ - \infty }^{t} {h_{j}^{(1)} (t - \tau )\zeta (\tau ){\text{d}}\tau },$$
(6)
$$F_{j}^{(2)} (t) = \int\limits_{ - \infty }^{t} {\int\limits_{ - \infty }^{t} {h_{j}^{(2)} (t - \tau_{1} ,t - \tau_{2} )} \zeta (\tau_{1} )\zeta (\tau_{2} ){\text{d}}\tau_{1} {\text{d}}\tau_{2} },$$
(7)

where hj(1)(t) and hj(2)(t) are the first- and second-order impulse response functions, respectively, which are acquired through the Fourier transform of the linear transfer function (LTF) LTFj(ω) and quadratic transfer function (QTF) QTFj(ωi, ωj) as follows:

$$h_{j}^{(1)} (t) = {\text{Re}} [\frac{1}{{\uppi }}\int\limits_{0}^{\infty } {LTF(\omega_{i} )} {\text{e}}^{{{\text{i}}\omega_{i} t}} {\text{d}}\omega ],$$
(8)
$$h_{j}^{(2)} (t_{1} ,t_{2} ) = {\text{Re}} [\frac{1}{{2{\uppi }^{2} }}\int\limits_{0}^{\infty } {\int\limits_{0}^{\infty } {QTF(\omega_{i} ,\omega_{j} ){\text{e}}^{{{\text{i(}}\omega_{i} t_{1} + \omega_{j} t_{2} )}} {\text{d}}\omega_{i} {\text{d}}\omega_{j} } } ].$$
(9)

2.5 Dynamic model of overall system

The swing suppression control system is composed of the HPPCD, compensation base, cargo, and lifting rope. By treating the HPPCD and cargo as particles and neglecting the mass and elastic deformation of the lifting rope, the coordinates of point Q are obtained as follows:

$$\left\{ {\begin{array}{*{20}l} {x_{Q} (t) = x_{P} (t) + x(t)} \\ {y_{Q} (t) = y_{P} (t) - y(t)} \\ {z_{Q} (t) = z_{P} (t) + z(t)} \\ \end{array} } \right.,$$
(10)

where xP(t), yP(t), and zP(t) are the disturbance of the boom-tip.

Then, the coordinate vector of the cargo in the geodetic coordinate can be obtained as follows:

$$\left\{ {\begin{array}{*{20}l} {x_{G} (t) = x_{P} (t) + x(t) + l\sin \alpha (t)\cos \beta (t)} \\ {y_{G} (t) = y_{P} (t) + y(t) - l\sin \beta (t)} \\ {z_{G} (t) = z_{P} (t) + z(t) + l\cos \alpha (t)\cos \beta (t)} \\ \end{array} } \right..$$
(11)

Taking the XPOPYP plane as the zero potential energy surface, the total kinetic energy and potential energy of the cargo system are derived as follows:

$$\begin{gathered} T = \frac{1}{2}m_{1} \left( {\dot{x}_{Q}^{2} + \dot{y}_{Q}^{2} + \dot{z}_{Q}^{2} + \dot{x}^{2} } \right. \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \left. { + \dot{y}^{2} + \dot{z}^{2} + 2\dot{x}\dot{x}_{Q} + 2\dot{y}\dot{y}_{Q} + 2\dot{z}\dot{z}_{Q} } \right) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + \frac{1}{2}m\left[ {\dot{x}_{Q}^{2} + \dot{y}_{Q}^{2} + \dot{z}_{Q}^{2} + 2\dot{y}_{Q} (\dot{y} - l\dot{\beta }\cos \beta )} \right. \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + 2\dot{x}_{Q} (\dot{x} + l\dot{\alpha }\cos \alpha \cos \beta - l\dot{\beta }\sin \alpha \sin \beta ) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + 2\dot{z}_{Q} (\dot{z} - l\dot{\alpha }\sin \alpha \cos \beta - l\dot{\beta }\cos \alpha \sin \beta ) \\ \, \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + \dot{x}^{2} + \dot{y}^{2} + \dot{z}^{2} + l^{2} \dot{\beta }^{2} + l^{2} \dot{\alpha }^{2} \cos^{2} \beta \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + 2\dot{x}(l\dot{\alpha }\cos \alpha \cos \beta - l\dot{\beta }\sin \alpha \sin \beta ) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \left. { - 2\dot{y}l\dot{\beta }\cos \beta - 2\dot{z}(l\dot{\alpha }\sin \alpha \cos \beta + l\dot{\beta }\cos \alpha \sin \beta )} \right] \\ \end{gathered},$$
(12)
$$V = m_{1} gz - mgl\cos \alpha \cos \beta.$$
(13)

The wind force and air resistance on the cargo, and the friction between the compensation base and the HPPCD are not considered. Then, by constructing the Lagrangian function L = T − V, selecting the generalized coordinates x, y, α, and β, the Lagrange function of the system is derived as follows:

$$\frac{\text{d}}{\text{d}t}\left( {\frac{\partial L}{{\partial \dot{x}}}} \right) - \frac{\partial L}{{\partial x}} = F_{x},$$
(14)
$$\frac{\text{d}}{\text{d}t}\left( {\frac{\partial L}{{\partial \dot{y}}}} \right) - \frac{\partial L}{{\partial y}} = F_{y},$$
(15)
$$\frac{\text{d}}{\text{d}t}\left( {\frac{\partial L}{{\partial \dot{\alpha }}}} \right) - \frac{\partial L}{{\partial \alpha }} = 0,$$
(16)
$$\frac{\text{d}}{\text{d}t}\left( {\frac{\partial L}{{\partial \dot{\beta }}}} \right) - \frac{\partial L}{{\partial \beta }} = 0.$$
(17)

Then, the dynamical equations of the overall system are derived as follows:

$$\begin{gathered} F_{x} = \left( {m_{1} + m} \right)\ddot{x} + \left( {m_{1} + m} \right)\ddot{x}_{P} + ml\cos \alpha \cos \beta \ddot{\alpha } \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - ml\sin \alpha \cos \beta \dot{\alpha }^{2} - 2ml\cos \alpha \sin \beta \dot{\alpha }\dot{\beta } \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - ml\sin \alpha \sin \beta \ddot{\beta } - ml\sin \alpha \cos \beta \dot{\beta }^{2} \\ \end{gathered},$$
(18)
$$F_{y} = \left( {m_{1} + m} \right)\ddot{y} + \left( {m_{1} + m} \right)\ddot{y}_{P} - ml\cos \beta \ddot{\beta } + ml\sin \beta \dot{\beta }^{2},$$
(19)
$$\begin{gathered} ml\cos \alpha \cos \beta \ddot{x} - ml\sin \alpha \cos \beta \ddot{z} + ml^{2} \cos^{2} \beta \ddot{\alpha } \\ - 2ml^{2} \sin \beta \cos \beta \dot{\alpha }\dot{\beta } + mgl\sin \alpha \cos \beta \\ + ml\cos \alpha \cos \beta \ddot{x}_{P} - ml\sin \alpha \cos \beta \ddot{z}_{P} = 0 \\ \end{gathered},$$
(20)
$$\begin{gathered} - m\ddot{x}_{P} l\sin \alpha \sin \beta - m\ddot{y}_{P} l\cos \beta - m\ddot{z}_{P} l\cos \alpha \sin \beta \\ - m\ddot{x}l\sin \alpha \sin \beta - m\ddot{y}l\cos \beta - m\ddot{z}l\cos \alpha \sin \beta \\ + ml^{2} \ddot{\beta } + ml^{2} \dot{\alpha }^{2} \cos \beta \sin \beta + mgl\cos \alpha \sin \beta = 0 \\ \end{gathered}.$$
(21)

Vectors are set as qa = [x, y]T and qb = [a, β]T. Then, from Eqs. (18), (19), (20) and (21), a state-space model is obtained as follows:

$${\boldsymbol M}_{11}(\boldsymbol q){\ddot{\boldsymbol q}}_a+{\boldsymbol M}_{12}(\boldsymbol q){\ddot{\boldsymbol q}}_{b}+{\boldsymbol C}_{11}(\boldsymbol q,\dot{\boldsymbol q})+{\boldsymbol G}_1(\boldsymbol q)={\boldsymbol F}_{a},$$
(22)
$${\boldsymbol{M}}_{21} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{a} + {\boldsymbol{M}}_{22} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{b} + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) = 0,$$
(23)

where Fa = [Fx, Fy]T is the control input matrix. Moreover, \({\boldsymbol{M}}_{11} = \left[ {\begin{array}{*{20}c} {m_{1} + m} & 0 \\ 0 & {m_{1} + m} \\ \end{array} } \right]\), \({\boldsymbol{M}}_{12} = \left[ {\begin{array}{*{20}c} {ml\cos \alpha \cos \beta } & { - ml\sin \alpha \sin \beta } \\ 0 & { - ml\cos \beta } \\ \end{array} } \right]\), \({\boldsymbol{M}}_{21} = \left[ {\begin{array}{*{20}c} {ml\cos \alpha \cos \beta } & 0 \\ { - ml\sin \alpha \sin \beta } & { - ml\cos \beta } \\ \end{array} } \right]\), \({\boldsymbol{M}}_{22} = \left[ {\begin{array}{*{20}c} {ml^{2} \cos^{2} \beta } & 0 \\ 0 & {ml^{2} } \\ \end{array} } \right]\), \({\boldsymbol{C}}_{11} = \left[ {\begin{array}{*{20}c} { - 2ml\cos \alpha \sin \beta \dot{\alpha }\dot{\beta } - ml\sin \alpha \cos \beta \dot{\alpha }^{2} - ml\sin \alpha \cos \beta \dot{\beta }^{2} } \\ {ml\sin \beta \dot{\beta }^{2} } \\ \end{array} } \right]\), \({\boldsymbol{C}}_{21} = \left[ {\begin{array}{*{20}c} { - 2ml^{2} \sin \beta \cos \beta \dot{\alpha }\dot{\beta }} \\ {ml^{2} \cos \beta \sin \beta \dot{\alpha }^{2} } \\ \end{array} } \right]\), \(G_{1} = \left[ {\begin{array}{*{20}c} {(m_{1} + m)\ddot{x}_{P} } \\ {(m_{1} + m)\ddot{y}_{P} } \\ \end{array} } \right]\), \({\boldsymbol{G}}_{2} = \left[ {\begin{array}{*{20}c} {{\boldsymbol{G}}_{21} } \\ {{\boldsymbol{G}}_{22} } \\ \end{array} } \right]\), \({\boldsymbol{\ddot{q}}}_{a} = \left[ {\begin{array}{*{20}c} {\ddot{x}} \\ {\ddot{y}} \\ \end{array} } \right]\), \({\boldsymbol{\ddot{q}}}_{b} = \left[ {\begin{array}{*{20}c} {\ddot{\alpha }} \\ {\ddot{\beta }} \\ \end{array} } \right]\),

where \(\begin{gathered} {\boldsymbol{G}}_{21} = - ml\sin \alpha \cos \beta \ddot{z} + mgl\sin \alpha \cos \beta \\ + ml\cos \alpha \cos \beta \ddot{x}_{P} - ml\sin \alpha \cos \beta \ddot{z}_{P} \\ \end{gathered}\) and \(\begin{gathered} {\boldsymbol{G}}_{22} = - ml\cos \alpha \sin \beta \ddot{z} - ml\sin \alpha \sin \beta \ddot{x}_{P} \\ - ml\cos \beta \ddot{y}_{P} - ml\cos \alpha \sin \beta \ddot{z}_{P} + mgl\cos \alpha \sin \beta \\ \end{gathered}\).

Substituting Eq. (23) into Eq. (22) results in

$$\begin{gathered} {\boldsymbol{M}}_{11} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{a} - {\boldsymbol{M}}_{12} ({\boldsymbol{q}}){\boldsymbol{M}}_{22}^{ - 1} ({\boldsymbol{q}})\left({\boldsymbol{M}}_{21} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{a} + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}\right) \\ + {\boldsymbol{G}}_{2} ({\boldsymbol{q}})) + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}}) = {\boldsymbol{F}}_{a} \\ \end{gathered}.$$
(24)

Substituting Eq. (22) into Eq. (23) results in the following:

$$\begin{gathered} - {\boldsymbol{M}}_{21} ({\boldsymbol{q}}){\varvec{M}}_{11}^{ - 1} ({\boldsymbol{q}})\left({\boldsymbol{M}}_{12} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{b} + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}})\right) + \\ {\boldsymbol{M}}_{22} ({\boldsymbol{q}}){\boldsymbol{\ddot{q}}}_{b} + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) = - {\boldsymbol{M}}_{11}^{ - 1} ({\boldsymbol{q}}){\boldsymbol{F}}_{a} \\ \end{gathered}.$$
(25)

Angles α and β are generally very small when the operation system is stable. In this case, the following equalities in approximations are \(\sin \alpha \approx \alpha\), \(\sin \beta \approx \beta\), \(\cos \alpha \approx 1\), \(\cos \beta \approx 1\), and

$$\sin \alpha \sin \beta \approx 0.$$
(26)

By Eq. (26), from Eqs. (24) and (25), the following is derived:

$$\begin{gathered} {\boldsymbol{M}}_{11} {\boldsymbol{\ddot{q}}}_{a} - {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} \left( {{\overline{\boldsymbol{M}}}_{21} {\boldsymbol{\ddot{q}}}_{a} + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}})} \right. \\ \left. { + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) + {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}})} \right) + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}}) = {\boldsymbol{F}}_{a} \\ \end{gathered},$$
(27)
$$\begin{gathered} - \overline{\boldsymbol{M}}_{21} {\varvec{M}}_{11}^{ - 1} ({\boldsymbol{q}}){\overline{\boldsymbol{M}}}_{12} \left( {{\boldsymbol{\ddot{q}}}_{b} + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}})} \right) \\ + {\overline{\boldsymbol{M}}}_{22} {\boldsymbol{\ddot{q}}}_{b} + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) + {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}}) = - {\boldsymbol{M}}_{11}^{ - 1} {\boldsymbol{F}}_{a} \\ \end{gathered},$$
(28)

where

\({\boldsymbol{M}}_{11} = \left[ {\begin{array}{*{20}c} {m_{1} + m} & 0 \\ 0 & {m_{1} + m} \\ \end{array} } \right]\),  \({\overline{\boldsymbol{M}}}_{12} = \left[ {\begin{array}{*{20}c} {ml} & 0 \\ 0 & { - ml} \\ \end{array} } \right]\),

\({\overline{\boldsymbol{M}}}_{21} = \left[ {\begin{array}{*{20}c} {ml} & 0 \\ 0 & { - ml} \\ \end{array} } \right]\),  \({\overline{\boldsymbol{M}}}_{22} = \left[ {\begin{array}{*{20}c} {ml^{2} } & 0 \\ 0 & {ml^{2} } \\ \end{array} } \right]\),

\({\boldsymbol{C}}_{11} = \left[ {\begin{array}{*{20}c} { - 2ml\beta \dot{\alpha }\dot{\beta } - ml\alpha \dot{\alpha }^{2} - ml\alpha \dot{\beta }^{2} } \\ {ml\beta \dot{\beta }^{2} } \\ \end{array} } \right]\), \({\boldsymbol{C}}_{21} = \left[ {\begin{array}{*{20}c} { - 2ml^{2} \beta \dot{\alpha }\dot{\beta }} \\ {ml^{2} \beta \dot{\alpha }^{2} } \\ \end{array} } \right]\), \({\boldsymbol{G}}_{1} = \left[ {\begin{array}{*{20}c} {(m_{1} + m)\ddot{x}_{P} } \\ {(m_{1} + m)\ddot{y}_{P} } \\ \end{array} } \right]\),

\({\boldsymbol{G}}_{2} = \left[ {\begin{array}{*{20}c} { - ml\alpha \ddot{z} + ml\ddot{x}_{P} - ml\alpha \ddot{z}_{P} } \\ { - ml\beta \ddot{z} - ml\alpha \beta \ddot{x}_{P} - ml\ddot{y}_{P} - ml\beta \ddot{z}_{P} } \\ \end{array} } \right]\), \({\tilde{\boldsymbol{G}}}_{2} = \left[ {\begin{array}{*{20}c} {mgl\alpha } \\ {mgl\beta } \\ \end{array} } \right]\).

Then, Eqs. (27) and (28) can be rewritten as follows:

$$\begin{gathered} {\overline{\boldsymbol{M}}}_{11} {\boldsymbol{\ddot{q}}}_{a} - {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} \left( {{\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) + {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}})} \right) \\ + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}}) = {\boldsymbol{F}}_{a} \\ \end{gathered},$$
(29)
$$\begin{gathered} {\tilde{\boldsymbol{M}}}_{22} {\boldsymbol{\ddot{q}}}_{b} - {\overline{\boldsymbol{M}}}_{21} {\boldsymbol{M}}_{11}^{ - 1} \left( {{\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}})} \right) \\ + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}}) + {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}}) = - {\overline{\boldsymbol{M}}}_{11}^{ - 1} {\boldsymbol{F}}_{a} \\ \end{gathered},$$
(30)

where \({\overline{\boldsymbol{M}}}_{11} = {\boldsymbol{M}}_{11} - {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} {\overline{\boldsymbol{M}}}_{21} = \left[ {\begin{array}{*{20}c} {m_{1} } & 0 \\ 0 & {m_{1} } \\ \end{array} } \right]\) and \({\tilde{\boldsymbol{M}}}_{22} = {\overline{\boldsymbol{M}}}_{22} - {\overline{\boldsymbol{M}}}_{21} {\boldsymbol{M}}_{11}^{ - 1} {\overline{\boldsymbol{M}}}_{12} = \left[ {\begin{array}{*{20}c} {\frac{{m_{1} ml^{2} }}{{m_{1} + m}}} & 0 \\ 0 & {\frac{{m_{1} ml^{2} }}{{m_{1} + m}}} \\ \end{array} } \right]\).

From Eqs. (29) and (30), the following can be derived:

$${\boldsymbol{\ddot{q}}}_{a} + {\overline{\boldsymbol{M}}}_{11}^{ - 1} {\boldsymbol{f}}_{a} - {\overline{\boldsymbol{M}}}_{11}^{ - 1} {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}}) = {\overline{\boldsymbol{M}}}_{11}^{ - 1} {\boldsymbol{F}}_{a},$$
(31)
$${\boldsymbol{\ddot{q}}}_{b} + {\tilde{\boldsymbol{M}}}^{ - 1}_{22} {\boldsymbol{f}}_{b} + {\tilde{\boldsymbol{M}}}^{ - 1}_{22} {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}}) = - {\tilde{\boldsymbol{M}}}^{ - 1}_{22} {\overline{\boldsymbol{M}}}_{11}^{ - 1} {\boldsymbol{F}}_{a},$$
(32)

where \({\boldsymbol{f}}_{a} = - {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} \left( {{\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}})} \right) + {\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}})\) and \({\boldsymbol{f}}_{b} = - {\overline{\boldsymbol{M}}}_{21} {\boldsymbol{M}}_{11}^{ - 1} \left( {{\boldsymbol{C}}_{11} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{1} ({\boldsymbol{q}})} \right) + {\boldsymbol{C}}_{21} ({\boldsymbol{q}},{\dot{\boldsymbol{q}}}) + {\boldsymbol{G}}_{2} ({\boldsymbol{q}})\).

Let \({\boldsymbol{x}}_{1} = \left[ {\begin{array}{*{20}c} {{\boldsymbol{q}}_{a} } \\ {{\boldsymbol{q}}_{b} } \\ \end{array} } \right]\), \({\boldsymbol{x}}_{2} = \left[ {\begin{array}{*{20}c} {{\dot{\boldsymbol{q}}}_{a} } \\ {{\dot{\boldsymbol{q}}}_{b} } \\ \end{array} } \right]\). Then, from Eqs. (31) and (32), the following can be derived:

$$\left\{ \begin{gathered} {\dot{\boldsymbol{x}}}_{1} = {\boldsymbol{x}}_{2} \\ {\dot{\boldsymbol{x}}}_{2} = \left[ {\begin{array}{*{20}c} {{\overline{\boldsymbol{M}}}_{11}^{ - 1} {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}})} \\ { - {\tilde{\boldsymbol{M}}}^{ - 1}_{22} {\tilde{\boldsymbol{G}}}_{2} ({\boldsymbol{q}})} \\ \end{array} } \right] + {\boldsymbol{F}}_{10} {\boldsymbol{f}}_{1} + {\boldsymbol{B}}_{u0} {\boldsymbol{F}}_{a} \\ \end{gathered} \right.,$$
(33)

where \({\boldsymbol{F}}_{10} = \left[ {\begin{array}{*{20}c} { - {\overline{\boldsymbol{M}}}_{11}^{ - 1} } & 0 \\ 0 & { - {\tilde{\boldsymbol{M}}}^{ - 1}_{21} } \\ \end{array} } \right]\), \({\boldsymbol{B}}_{u0} = \left[ {\begin{array}{*{20}c} {{\overline{\boldsymbol{M}}}_{11}^{ - 1} } \\ {{\tilde{\boldsymbol{M}}}^{ - 1}_{22} {\overline{\boldsymbol{M}}}_{11}^{ - 1} } \\ \end{array} } \right]\), and \({\boldsymbol{f}}_{1} = \left[ {\begin{array}{*{20}c} {f_{a} } \\ {f_{b} } \\ \end{array} } \right]\), which can be written as follows:

$${\dot{\boldsymbol{x}}} = {\boldsymbol{A\dot{x}}} + {\boldsymbol{B}}_{0} {\boldsymbol{F}}_{10} {\boldsymbol{f}}_{1} + {\boldsymbol{B}}_{0} {\boldsymbol{B}}_{u0} {\boldsymbol{F}}_{a},$$
(34)

where \({\boldsymbol{A}} = \left[ {\begin{array}{*{20}c} 0 & 0 & {\boldsymbol{I}} & 0 \\ 0 & 0 & 0 & {\boldsymbol{I}} \\ {mgl{\overline{\boldsymbol{M}}}_{11}^{ - 1} {\overline{\boldsymbol{M}}}_{12} {\overline{\boldsymbol{M}}}_{22}^{ - 1} } & 0 & 0 & 0 \\ { - mgl{\tilde{\boldsymbol{M}}}^{ - 1}_{22} } & 0 & 0 & 0 \\ \end{array} } \right]\), and \({\boldsymbol{B}}_{0} = \left[ {\begin{array}{*{20}c} 0 \\ {\boldsymbol{I}} \\ \end{array} } \right]\). Let \({\boldsymbol{F}}_{1} = {\boldsymbol{B}}_{0} {\boldsymbol{F}}_{10}\), \({\boldsymbol{B}}_{u} = {\boldsymbol{B}}_{0} {\boldsymbol{B}}_{u0}\). Then, from Eq. (34),

$${\dot{\boldsymbol{x}}} = {\boldsymbol{A\dot{x}}} + {\boldsymbol{F}}_{1} {\boldsymbol{f}}_{1} \left( {{\boldsymbol{x}}(t)} \right) + {\boldsymbol{B}}_{u} {\boldsymbol{u}} + {\boldsymbol{B}}_{d} {\boldsymbol{d}}(t),$$
(35)

where \({\boldsymbol{u}} = \left[ {\begin{array}{*{20}c} {F_{ax} } \\ {F_{ay} } \\ \end{array} } \right]\), and \({\boldsymbol{B}}_{d} = {\boldsymbol{B}}_{u}\). According to Eqs. (5), (6), (7), (8) and (9), the wave forces \({F}_{wx},{F}_{wy}\) in Eqs. (3) and (4) always can be generated by the following nonlinear exosystem:

$$\left\{ \begin{gathered} \dot{\boldsymbol{\zeta }}(t) = \boldsymbol{W\zeta }(t) + {\varvec{F}}_{{2}} {\varvec{f}}_{{2}} \left( {{\varvec{\zeta}}(t)} \right) \\ {\varvec{d}}(t) = \boldsymbol{V\zeta }(t) \\ \end{gathered} \right.,$$
(36)

where \({\varvec{\zeta}}(t) \in {\mathbb{R}}^{2}\) and \({\varvec{d}}(t) = \left[ {\begin{array}{*{20}c} {F_{wx} } \\ {F_{wy} } \\ \end{array} } \right] \in {\mathbb{R}}^{2}\) represent the exosystem state and the wave force disturbance, respectively; \({\varvec{W}} \in {\mathbb{R}}^{{n_{\zeta } \times n_{\zeta } }}\), \({\varvec{V}} \in {\mathbb{R}}^{{n_{d} \times n_{\zeta } }}\), and \({\varvec{F}}_{2} \in {\mathbb{R}}^{2 \times 1}\) are known matrices; and \(\varvec f_{2} \left( {{\varvec{\zeta}}(t)} \right) \in {\mathbb{R}}\) is an unknown function due to the wave observation error and coupling from the high-order wave forces.

2.6 RBF FLS

Because system Eq. (35) and exosystem Eq. (36) contain unknown nonlinear functions, the FLSs are utilized to estimate the nonlinearities. The property of the FLS is presented by Lemma 1.

Lemma 1: Let g(x) be a continuous function, which is defined on a compact set \(U\subseteq {{\varvec{R}}}^{n}\). Then, for any constant \(\varepsilon >0\), an RBF FLS exists (Wang 1993)

$$f(x) = {\varvec{\theta}}^{{\text{T}}} {\varvec{\eta}}(x),$$
(37)

such that

$$\mathop {\sup }\limits_{x \in U} \left| {f\left( x \right) - g\left( x \right)} \right| \le \varepsilon,$$

where \({\varvec{\theta}} = [\begin{array}{*{20}c} {\theta_{1} ,} & {\theta_{2} ,} & { \ldots ,} & {\theta_{m} } \\ \end{array} ]^{{\text{T}}}\) is the weight vector, \({\varvec{\eta}}(x) = [\begin{array}{*{20}c} {\eta_{1} (x),} & {\eta_{2} (x),} & { \ldots ,} & {\eta_{m} (x)} \\ \end{array} ]^{{\text{T}}}\) is the fuzzy basis function vector with fuzzy membership functions that are all chosen as Gaussian functions, ε is the minimum fuzzy approximation error, and m is the number of the inference fuzzy rules.

2.7 Control objective

The objective of this work is to design a fuzzy control law to make \({{\varvec{q}}}_{b}\) in Eq. (35) as small as possible such that the closed-loop system Eq. (35) is bounded in the presence of uncertainties and the wave forces.

The following assumptions are made to facilitate the suppression control design.

Assumption 1: The nonlinear functions \({{\varvec{f}}}_{i} \left({\varvec{x}}\left(t\right)\right)\) and \({{\varvec{f}}}_{2}\left(\varvec\zeta \left(t\right)\right)\) are unknown but bounded.

Assumption 2: The pair \(\left({\varvec{A}},\boldsymbol{ }{{\varvec{B}}}_{u}\right)\) is controllable and the pair \(\left(\boldsymbol{W},\;{\boldsymbol{B}}_{\boldsymbol{d}}\;\boldsymbol{V}\right)\) is detectable.

3 Define the concept of design of FDOBC and FDO

3.1 Adaptive fuzzy approximation

According to Lemma 1, the RBF FLS is established to estimate the unknown nonlinear function \({\varvec{f}}_{1}\) and \({\varvec{f}}_{2} ({\varvec{\zeta}}(t))\) as follows:

$$\hat{\boldsymbol{f}}_{1} \left( {{\boldsymbol{x}}(t)} \right) = {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} \left( {{\boldsymbol{x}}(t)} \right),$$
(38)
$$\hat{\boldsymbol{f}}_{2} \left( {{\varvec{\zeta}}(t)} \right) = {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {{\varvec{\zeta}}(t)} \right),$$
(39)

where \({\varvec{\theta}}_{{f_{1} }}^{ * }\) and \({\varvec{\theta}}_{{f_{2} }}^{ * }\) are the optimal vectors. The approximated function \(\hat{\boldsymbol{f}}_{1} \left( {{\boldsymbol{x}}(t)} \right)\) in the FLS is in the form of a vector, and the corresponding adaptive update parameters \({\varvec{\theta}}_{{f_{1} }}^{{\text{T}}}\) and \({\varvec{\theta}}_{{f_{2} }}^{{\text{T}}}\) are matrices with appropriate dimensions. Fuzzy basis functions \({\varvec{\eta}}_{1} \left( {{\boldsymbol{x}}(t)} \right)\) and \({\varvec{\eta}}_{2} \left( {{\varvec{\zeta}}(t)} \right)\) are also matrices with appropriate dimensions.

However, \({\varvec{\zeta}}(t)\) in not available in practice because it is not measurable. Hence, an observer must be developed to produce its estimates \(\hat{\boldsymbol{\zeta }}(t)\) to replace \({\varvec{\zeta}}(t)\) in Eq. (39) to obtain

$$\hat{\boldsymbol{f}}_{2} \left( {{\varvec{\zeta}}(t)} \right) = {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right).$$
(40)

3.2 FDO and FDOBC structure

To approximate the external disturbance \({\varvec{d}}(t)\) of a nonlinear exosystem, based on Eqs. (36), (38), and (40), an FDO is designed as follows (Cummins 1962):

$$\begin{gathered} \dot{\boldsymbol{\xi }}(t) = \left( {{\varvec{W}} - {\varvec{LB}}_{d} {\varvec{V}}} \right)\left( {{\varvec{\xi}}(t) + {\varvec{Lx}}(t)} \right) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} + {\varvec{F}}_{2} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {{\varvec{\xi}}(t) + {\varvec{Lx}}(t)} \right) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - {\varvec{L}}\left( {{\varvec{Ax}}(t) + {\varvec{F}}_{1} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x) + {\varvec{B}}_{u} {\varvec u}(t)} \right) \\ \end{gathered},$$
(41)
$$\left\{ \begin{gathered} \hat{\boldsymbol{\zeta }}(t) = {\varvec{\xi}}(t) + {\varvec{Lx}}(t) \\ \hat{\boldsymbol{d}}(t) = \boldsymbol{V\hat{\zeta }}(t) \\ \end{gathered} \right.,$$
(42)

where \({\varvec{\xi}}(t)\) is the intermediate variable.

Based on Eqs. (38), (41), and (42), a composite FDOBC law is designed as follows:

$$\varvec u(t) = {\varvec{Kx}}(t) - \boldsymbol{M\hat{d}}(t) - \boldsymbol{N\hat{f}}_{{1}} \left( {{\varvec{x}}(t)} \right),$$
(43)

where \({\varvec{K}} \in {\mathbb{R}}^{{n_{u} \times n_{x} }}\) is the controller gain matrix to be designed.

The estimation error of \({\varvec{\zeta}}(t)\) is defined as follows:

$${\varvec{e}}_{\zeta } (t) = {\varvec{\zeta}}(t) - \hat{\boldsymbol{\zeta }}(t).$$
(44)

Taking the derivatives with respect to time t on both sides of Eq. (44), and noting Eq. (42),

$$\begin{gathered} \dot{\boldsymbol{e}}_{\zeta } (t) = ({\varvec{W}} - {\varvec{LB}}_{d} {\varvec{V}}){\varvec{e}}_{\zeta } (t) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} + {\varvec{F}}_{2} \left[ {{\varvec{\theta}}_{{f_{2} }}^{{*{\text{T}}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) - {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) + \Delta {\varvec{f}}_{2} } \right] \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} - {\varvec{LF}}_{1} \left[ {{\varvec{\theta}}_{{f_{1} }}^{{*{\text{T}}}} {\varvec{\eta}}_{1} (x) - {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x) + \Delta {\varvec{f}}_{1} } \right] \\ \end{gathered},$$
(45)

with \(\Delta {\varvec{f}}_{1} = {\varvec{f}}_{1} (x) - {\varvec{\theta}}_{{f_{1} }}^{{*{\text{T}}}} {\varvec{\eta}}_{1} (x),\Delta {\varvec{f}}_{2} = {\varvec{f}}_{2} ({\varvec{\zeta}}(t)) - {\varvec{\theta}}_{{f_{2} }}^{{*{\text{T}}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)\).

By substituting Eq. (43) into Eq. (35), the following is acquired:

$$\begin{array}{c}\dot {\varvec x}(t)=\left(\boldsymbol A+{\boldsymbol B}_u\boldsymbol K\right)\varvec x(t)+{\boldsymbol B}_d\boldsymbol V{\boldsymbol e}_\zeta(t)\\\begin{array}{cc}&\end{array}+{\boldsymbol F}_1\left[\boldsymbol\theta_{f_1}^{\ast\text{T}}{\boldsymbol\eta}_1(x)-\boldsymbol\theta_{f_1}^\text{T}{\boldsymbol\eta}_1(x)+{\boldsymbol f}_1\right]\end{array}.$$
(46)

By Eqs. (45) and (46), a composite system is derived as follows:

$$\begin{array}{c}\dot{\widetilde{\boldsymbol x}}(t)=\overset{\boldsymbol\sim}{\boldsymbol A}\overset{\boldsymbol\sim}{\boldsymbol x}(t)+{\widetilde{\boldsymbol F}}_1\left[\boldsymbol\theta_{f_1}^{\ast\text{T}}{\boldsymbol\eta}_1(x)-\boldsymbol\theta_{f_1}^\text{T}{\boldsymbol\eta}_1(x)+\triangle{\boldsymbol f}_1\right]\\+{\widetilde{\boldsymbol F}}_2\left[\boldsymbol\theta_{f_2}^{\ast \text T}{\boldsymbol\eta}_2\left(\widehat{\boldsymbol\zeta}(t)\right)-\boldsymbol\theta_{f_2}^\text T{\boldsymbol\eta}_2\left(\widehat{\boldsymbol\zeta}(t)\right)+\triangle{\boldsymbol f}_2\right]\end{array},$$
(47)

where \(\tilde{\boldsymbol{x}}(t) = \left[ {\begin{array}{*{20}c} {{\varvec{x}}(t)} \\ {{\varvec{e}}_{\zeta } (t)} \\ \end{array} } \right]\), \(\tilde{\boldsymbol{A}} = \left[ {\begin{array}{*{20}c} {\boldsymbol{A} + \boldsymbol{B}_{u} {\varvec{K}}} & {{\varvec{B}}_{d} {\varvec{V}}} \\ 0 & {{\varvec{W}} - {\varvec{LB}}_{d} {\varvec{V}}} \\ \end{array} } \right]\), \(\tilde{\boldsymbol{F}}_{1} = \left[ {\begin{array}{*{20}c} {{\varvec{F}}_{1} } \\ { - {\varvec{LF}}_{1} } \\ \end{array} } \right]\), \(\tilde{\boldsymbol{F}}_{2} = \left[ {\begin{array}{*{20}c} 0 \\ {{\varvec{F}}_{2} } \\ \end{array} } \right]\).

4 Design of FDOBCL and stability analysis

For the system Eq. (47), a Lyapunov function is selected as follows:

$$\varvec V=\widetilde{\boldsymbol x}^\text{T}\overset{\boldsymbol\sim}{\boldsymbol P}\overset{\boldsymbol\sim}{\boldsymbol x}+\frac1{\gamma_1}\overset{\boldsymbol\sim}{\boldsymbol\theta}_{f_1}^\text T{\overset{\boldsymbol\sim}{\boldsymbol\theta}}_{f_1}+\frac1{\gamma_2}\overset{\boldsymbol\sim}{\boldsymbol\theta}_{f_2}^\text T{\overset{\boldsymbol\sim}{\boldsymbol\theta}}_{f_2},$$
(48)

where \(\tilde{\boldsymbol{P}} \in {\mathbb{R}}^{{(n_{x} + n_{\zeta } ) \times (n_{x} + n_{\zeta } )}}\), and \(\tilde{\boldsymbol{P}} > 0\). The time derivative of \(\boldsymbol V\) along the trajectories of the system Eq. (48) is calculated as follows:

$$\begin{array}{l}\begin{array}{ll}\boldsymbol V=&\widetilde{\boldsymbol x}^\text{T}\left(\overset{\boldsymbol\sim}{\boldsymbol P}\overset{\boldsymbol\sim}{\boldsymbol A}+\overset{\boldsymbol\sim}{\boldsymbol A}^{\mathrm T}\overset{\boldsymbol\sim}{\boldsymbol P}\right)\widetilde{\boldsymbol x}+2\overset{\boldsymbol\sim}{\boldsymbol x}^{\mathrm T}\overset{\boldsymbol\sim}{\boldsymbol P}{\overset{\boldsymbol\sim}{\boldsymbol F}}_1\Delta{\boldsymbol f}_1+2\overset{\boldsymbol\sim}{\boldsymbol x}^{\mathrm T}\overset{\boldsymbol\sim}{\boldsymbol P}{\overset{\boldsymbol\sim}{\boldsymbol F}}_2\Delta{\boldsymbol f}_2\\&+\frac2{\gamma_1}\overset{\boldsymbol\sim}{\boldsymbol\theta}_{f_1}^\text T\left(\gamma_1\overset{\boldsymbol\sim}{\boldsymbol x}^\text{T}\overset{\boldsymbol\sim}{\boldsymbol P}{\overset{\boldsymbol\sim}{\boldsymbol F}}_{1}{\boldsymbol\eta}_1(x)-{\dot{\boldsymbol\theta}}_{f_1}\right)\\&+\frac2{\gamma_2}\overset{\boldsymbol\sim}{\boldsymbol\theta}_{f_2}^\text T\left(\gamma_2\overset{\boldsymbol\sim}{\boldsymbol x}^\text{T}\overset{\boldsymbol\sim}{\boldsymbol P}{\overset{\boldsymbol\sim}{\boldsymbol F}}_{2}{\boldsymbol\eta}_2\left(\widehat{\boldsymbol\zeta}(t)\right)-{\dot{\boldsymbol\theta}}_{f_2}\right)\end{array}\end{array},$$
(49)

where \(\tilde{\boldsymbol{\theta }}_{{f_{{1}} }} = {\varvec{\theta}}_{{f_{1} }}^{*} - {\varvec{\theta}}_{{f_{{1}} }}\), \(\tilde{\boldsymbol{\theta }}_{{{\varvec{f}}_{2} }} = {\varvec{\theta}}_{{f_{2} }}^{*} - {\varvec{\theta}}_{{{\varvec{f}}_{2} }}\).

To eliminate terms \(\frac{2}{{\gamma_{1} }}\tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} \left( {\gamma_{1} \tilde{\boldsymbol{x}}^{{\text{T}}} {\tilde{\boldsymbol P}\tilde{\boldsymbol F}}_{{1}} {\varvec{\eta}}_{1} (x)} \right)\) and \(\frac{2}{{\gamma_{2} }}\tilde{\boldsymbol{\theta }}_{{f_{2} }}^{\text T} \left( {\gamma_{2} \tilde{\boldsymbol{x}}^{{\text{T}}} {\tilde{\boldsymbol P}\tilde{\boldsymbol F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)} \right)\) in Eq. (49), the parameter updating law should be selected as follows:

$$\dot{\boldsymbol{\theta }}_{{f_{1} }} = \gamma_{1} \tilde{\boldsymbol{x}}^{{\text{T}}} {\tilde{\boldsymbol P}\tilde{\boldsymbol F}}_{{1}} {\varvec{\eta}}_{1} \left( {{\varvec{x}}( t )} \right),$$
(50)
$$\dot{\boldsymbol{\theta }}_{{f_{{2}} }} = \gamma_{2} \tilde{\boldsymbol{x}}^{{\text{T}}} {\tilde{\boldsymbol P}\tilde{\boldsymbol F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right).$$
(51)

However, the value of \({\varvec{e}}_{\zeta } (t)\) should be known to implement the adaptive updating Eqs. (50) and (51), but it is not available in practice. Instead, to generate its estimation value \({\widehat{{\varvec{e}}}}_{\zeta}\left({t}\right)\), a novel DEEO is designed as follows:

$$\left\{ \begin{gathered} \user2{\dot{\hat{\tilde{x}}}}(t) = \user2{\tilde{A}\hat{\tilde{x}}}(t) + {\tilde{\boldsymbol{L}}}(y_{{\tilde{x}}} - \hat{y}_{{\hat{\tilde{x}}}} ) \\ \hat{ y}_{{\hat{\tilde{x}}}} = {\tilde{\boldsymbol{C}}}\user2{\hat{\tilde{x}}}(t) \\ \end{gathered} \right..$$
(52)

where \(\boldsymbol{\hat{\tilde{x}}}(t) = \left[ {\begin{array}{*{20}c} {\hat{\boldsymbol{x}}^{{\text{T}}} (t)} & {\hat{\boldsymbol{e}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]^{{\text{T}}}\), \({\tilde{\boldsymbol{C}}} = [\begin{array}{*{20}c} {\boldsymbol{I}} & 0 \\ \end{array} ]\), and the gain matrix \({\tilde{\boldsymbol{L}}}\) should be selected to make \(\left( {\tilde{\boldsymbol{A}} - {{\tilde{\boldsymbol L}\tilde{\boldsymbol C}}}} \right)\) a Hurwitz matrix. In this case, the following estimation error system is stable in the absence of an approximation error.

$${\dot{\boldsymbol{e}}}_{{\hat{\tilde{x}}}} = \boldsymbol{\dot{\tilde{x}}}(t) - \boldsymbol{\dot{\hat{\tilde{x}}}}(t) = (\tilde{\boldsymbol{A}} - {\boldsymbol{\tilde{L}\tilde{C}}}){\boldsymbol{e}}_{{\hat{\tilde{x}}}}.$$
(53)

Based on Eq. (52), \(\boldsymbol{\overline{\tilde{x}}} = \left[ {\begin{array}{*{20}c} {{\varvec{x}}^{{\text{T}}} } & {\hat{\boldsymbol{e}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]\). Then, the parameter update law is redesigned as follows:

$$\begin{gathered} \dot{\boldsymbol{\theta }}_{{f_{1} }} = \gamma_{1} {\boldsymbol{\overline{\tilde{x}}}}\left[ {\begin{array}{*{20}c} {{\varvec{P}}_{1} } & 0 \\ 0 & {{\varvec{P}}_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\varvec{F}}_{1} } \\ { - {\varvec{LF}}_{1} } \\ \end{array} } \right]{\varvec{\eta}}_{1} (x) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} = \gamma_{1} {\varvec{x}}^{{\text{T}}} {\varvec{P}}_{1} {\varvec{F}}_{{1}} {\varvec{\eta}}_{1} ({\varvec{x}}) - \gamma_{1} {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} {\varvec{P}}_{2} {\varvec{LF}}_{{1}} {\varvec{\eta}}_{1} (x) \\ \end{gathered},$$
(54)
$$\begin{gathered} \dot{\boldsymbol{\theta }}_{{f_{2} }} = \gamma_{2} {\boldsymbol{\overline{\tilde{x}}}}\left[ {\begin{array}{*{20}c} {{\varvec{P}}_{1} } & 0 \\ 0 & {{\varvec{P}}_{2} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} 0 \\ {{\varvec{F}}_{2} } \\ \end{array} } \right]{\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} = \gamma_{2} {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} {\varvec{P}}_{2} {\varvec{F}}_{2} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) \\ \end{gathered}.$$
(55)

To guarantee that the parameters of the update law are bounded, the projection algorithm is adopted as follows:

$$\dot{\boldsymbol{\theta }}_{{f_{1} }} = \left\{ \begin{gathered} \gamma_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\eta}}_{1} (x),\begin{array}{*{20}c} {\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} \begin{gathered} \left\| {{\varvec{\theta}}_{{f_{1} }} } \right\| < M_{{f_{1} }} {\kern 1pt} {\kern 1pt} {\text{or}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left\| {{\varvec{\theta}}_{{f_{1} }} } \right\| = M_{{f_{1} }} \\ {\text{and}}{\kern 1pt} {\kern 1pt} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x) \le 0 \\ \end{gathered} \\ \end{array} } & {} \\ \end{array} \\ P_{{f_{1} }} \left[ {\gamma_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\eta}}_{1} (x)} \right],\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\| = M_{{f_{1} }} } \\ {{\text{and}}{\kern 1pt} {\kern 1pt} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x) > 0} \\ \end{array} \\ \end{gathered} \right.,$$
(56)
$$\dot{\boldsymbol{\theta }}_{{f_{2} }} = \left\{ \begin{gathered} \gamma_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right),\begin{array}{*{20}c} {} & {\begin{array}{*{20}c} {\left\| {{\varvec{\theta}}_{{f_{2} }} } \right\| < M_{{f_{2} }} {\kern 1pt} {\kern 1pt} {\text{or}}{\kern 1pt} {\kern 1pt} {\kern 1pt} \left\| {{\varvec{\theta}}_{{f_{2} }} } \right\| = M_{{f_{2} }} } \\ {\begin{array}{*{20}c} {} \\ \end{array} {\text{and}}{\kern 1pt} {\kern 1pt} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{2} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) \le 0} \\ \end{array} } & {} \\ \end{array} \\ P_{{f_{2} }} \left[ {\gamma_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)} \right],\begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {\left\| {{\varvec{\theta}}_{{f_{2} }} } \right\| = M_{{f_{2} }} } \\ {{\text{and}}{\kern 1pt} {\kern 1pt} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{2} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) > 0} \\ \end{array} \\ \end{gathered} \right.,$$
(57)

where \(P_{{f_{1} }} \left[ \bullet \right]\) and \(P_{{f_{2} }} \left[ \bullet \right]\) are the projection operators defined as

$$\begin{aligned} P_{{f_{1} }} \left[ {\gamma_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\eta}}_{1} (x)} \right] &= \gamma_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\eta}}_{1} (x) \\ &- \gamma_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \frac{{{\varvec{\theta}}_{{f_{1} }} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x)}}{{\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\|^{2} }} \\ \end{aligned},$$
(58)
$$\begin{aligned} P_{{f_{2} }} \left[ {\gamma_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)} \right] &= \gamma_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right) \\& - \gamma_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} \frac{{{\varvec{\theta}}_{{f_{2} }} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)}}{{\left\| {{\varvec{\theta}}_{{f_{2} }} } \right\|^{2} }} \\ \end{aligned},$$
(59)

where \(M_{{f_{1} }}\), \(M_{{f_{2} }}\) are the parameter boundaries selected by the designer.

Substituting Eqs. (56) and (57) into Eq. (49) derives

$$\begin{aligned} \dot{V} = &\tilde{\boldsymbol{x}}^{{\text{T}}} \left( {\boldsymbol{\tilde{P}\tilde{A}} + \tilde{\boldsymbol{A}}^{{\text{T}}} \tilde{\boldsymbol{P}}} \right)\tilde{\boldsymbol{x}} + 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \Delta {\varvec{f}}_{1} \tau_{3} > 0 \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&+ 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{2} \Delta {\varvec{f}}_{2} + 2\left[ {\begin{array}{*{20}c} 0 & {{\boldsymbol{e}}_{\zeta }^{{\text{T}}} - {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]\tilde{\boldsymbol{P}}{\tilde{\boldsymbol{F}}}_{1} \tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} {{\varvec{\eta}}}_{{{1}}} \left( x \right) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&+ 2\left[ {\begin{array}{*{20}c} 0 & {{\boldsymbol{e}}_{\zeta }^{{\text{T}}} - {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]\tilde{\boldsymbol{P}}{\tilde{\boldsymbol{F}}}_{2} \tilde{\boldsymbol{\theta }}_{{f_{2} }}^{\text T} {{\varvec{\eta}}}_{2} \left( {{\hat{\boldsymbol{\zeta }}}\left( t \right)} \right) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&+ n_{1} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \frac{{\tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} {\varvec{\theta}}_{{f_{1} }} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x)}}{{\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\|^{2} }} + n_{2} \boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} \frac{{\tilde{\boldsymbol{\theta }}_{{f_{2} }}^{{\text{T}}} {\varvec{\theta}}_{{f_{2} }} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)}}{{\left\| {{\varvec{\theta}}_{{f_{2} }} } \right\|^{2} }} \\ \end{aligned}.$$
(60)

When the first row of Eq. (56) holds, \({n}_{1}=0\). When the second row of Eq. (56) holds, \({n}_{1}=1\). When the first row of Eq. (57) holds, \({n}_{2}=0\). When the second row of Eq. (57) holds, \({n}_{2}=1\). When \(n_{1} = 0\) and \(n_{2} = 0\), the following can be obtained:

$$\begin{aligned} \dot{V} &= \tilde{\boldsymbol{x}}^{{\text{T}}} \left( {\boldsymbol{\tilde{P}\tilde{A}} + \tilde{\boldsymbol{A}}^{{\text{T}}} \tilde{\boldsymbol{P}}} \right)\tilde{\boldsymbol{x}} + 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \Delta {\varvec{f}}_{1} \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&+ 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{2} \Delta {\varvec{f}}_{2} + 2\left[ {\begin{array}{*{20}c} 0 & {{\boldsymbol{e}}_{\zeta }^{{\text{T}}} - {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]\tilde{\boldsymbol{P}}{\tilde{\boldsymbol{F}}}_{1} \tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} {{\varvec{\eta}}}_{1} \left( x \right) \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \\&+ 2\left[ {\begin{array}{*{20}c} 0 & {{\boldsymbol{e}}_{\zeta }^{{\text{T}}} - {\hat{\boldsymbol{e}}}_{\zeta }^{{\text{T}}} } \\ \end{array} } \right]\tilde{\boldsymbol{P}}{\tilde{\boldsymbol{F}}}_{{2}} \tilde{\boldsymbol{\theta }}_{{f_{2} }}^{\text T} {{\varvec{\eta}}}_{2} \left( {{\hat{\boldsymbol{\zeta }}}\left( t \right)} \right) \\ \end{aligned},$$
(61)

where \(\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\| = M_{{f_{1} }}\) and \(\boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{1}} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x) > 0\). Because \(\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\| = M_{{f_{1} }} \ge \left\| {{\varvec{\theta}}_{{f_{1} }}^{*} } \right\|\),

$$\begin{aligned} \tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} {\varvec{\theta}}_{{f_{1} }} &= \left( {{\varvec{\theta}}_{{f_{1} }}^{*} - {\varvec{\theta}}_{{f_{{1}} }} } \right)^{{\text{T}}} {\varvec{\theta}}_{{f_{1} }} \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \\&= - \frac{1}{2}\left[ {\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\|^{2} - \left\| {{\varvec{\theta}}_{{f_{1} }}^{*} } \right\|^{2} + \left\| {{\varvec{\theta}}_{{f_{1} }} - {\varvec{\theta}}_{{f_{1} }}^{*} } \right\|^{2} } \right] < 0 \\ \end{aligned},$$
(62)

which implies \(\boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \frac{{\tilde{\boldsymbol{\theta }}_{{f_{1} }}^{{\text{T}}} {\varvec{\theta}}_{{f_{1} }} {\varvec{\theta}}_{{f_{1} }}^{{\text{T}}} {\varvec{\eta}}_{1} (x)}}{{\left\| {{\varvec{\theta}}_{{f_{1} }} } \right\|^{2} }}\) is not positive. Similarly, \(\boldsymbol{\overline{\tilde{x}}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{{2}} \frac{{\tilde{\boldsymbol{\theta }}_{{f_{2} }}^{{\text{T}}} {\varvec{\theta}}_{{f_{2} }} {\varvec{\theta}}_{{f_{2} }}^{{\text{T}}} {\varvec{\eta}}_{2} \left( {\hat{\boldsymbol{\zeta }}(t)} \right)}}{{\left\| {{\varvec{\theta}}_{{f_{2} }} } \right\|^{2} }}\) is not positive.

Then, from Eqs. (60) and (61),

$$\begin{gathered} \dot{V} \le \tilde{\boldsymbol{x}}^{{\text{T}}} \left( {\boldsymbol{\tilde{P}\tilde{A}} + \tilde{\boldsymbol{A}}^{{\text{T}}} \tilde{\boldsymbol{P}}} \right)\tilde{\boldsymbol{x}} + 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{1} \Delta {\varvec{f}}_{1} + 2\tilde{\boldsymbol{x}}^{{\text{T}}} \boldsymbol{\tilde{P}\tilde{F}}_{2} \Delta {\varvec{f}}_{2} \\ \begin{array}{*{20}c} {} & {} \\ \end{array} - 2\left( {{\boldsymbol{e}}_{\zeta }^{{\text{T}}} - \hat{\boldsymbol{e}}_{\zeta }^{{\text{T}}} } \right){\varvec{P}}_{2} \boldsymbol{LF}\hat{\boldsymbol{f}}_{1} + 2\left( {\boldsymbol{e}_{\zeta }^{{\text{T}}} - \hat{\boldsymbol{e}}_{\zeta }^{{\text{T}}} } \right){\varvec{P}}_{2} \boldsymbol{F}_{2} \hat{\boldsymbol{f}}_{2} \\ \end{gathered}.$$
(63)

The following is defined:

\(\boldsymbol{\omega }_{1}^{{\text{T}}} = \left[ {\begin{array}{*{20}c} {\tilde{\boldsymbol{x}}^{{\text{T}}} } & {\boldsymbol{e}_{\zeta }^{{\text{T}}} - \hat{\boldsymbol{e}}_{\zeta }^{{\text{T}}} } & {\Delta {\boldsymbol{f}}_{1}^{{\text{T}}} } & {\Delta {\boldsymbol{f}}_{2}^{{\text{T}}} } & {\hat{\boldsymbol{f}}_{1} } & {\hat{\boldsymbol{f}}_{2} } \\ \end{array} } \right]\),

\(\varvec{\Lambda }_{{1}} = \left[ {\begin{array}{*{20}c} {{\tilde{\boldsymbol P}\tilde{\boldsymbol A}} + *} & * & * & * & * & * \\ 0 & { - \tau_{1} \boldsymbol{I}} & * & * & * & * \\ {\tilde{\boldsymbol{F}}_{{1}}^{{\text{T}}} \tilde{\boldsymbol{P}}} & 0 & { - \tau_{2} \boldsymbol{I}} & * & * & * \\ {\tilde{\boldsymbol{F}}_{{2}}^{{\text{T}}} \tilde{\boldsymbol{P}}} & 0 & 0 & { - \tau_{3} \boldsymbol{I}} & * & * \\ 0 & { - \boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{L}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & { - \tau_{4} \boldsymbol{I}} & * \\ 0 & {\boldsymbol{F}_{{2}}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & 0 & { - \tau_{5} \boldsymbol{I}} \\ \end{array} } \right]\).

Then, by the Young equality, from Eq. (63) the following is derived:

$$\begin{aligned} \dot{V} &\le \boldsymbol{\omega }_{{1}}^{{\text{T}}} \varvec{\Lambda }_{{1}} \boldsymbol{\omega }_{1} + \tau_{1} \left( {\boldsymbol{e}_{\zeta } - \hat{\boldsymbol{e}}_{\zeta } } \right)^{{\text{T}}} \left( {\boldsymbol{e}_{\zeta } - \hat{\boldsymbol{e}}_{\zeta } } \right) \\ \begin{array}{*{20}c} {} \\ \end{array} \begin{array}{*{20}c} {} \\ \end{array} \\&+ \tau_{2} \Delta {\varvec{f}}_{{1}}^{{\text{T}}} \Delta {\varvec{f}}_{1} + \tau_{3} \Delta {\varvec{f}}_{2}^{{\text{T}}} \Delta {\varvec{f}}_{2} + \tau_{4} \hat{\boldsymbol{f}}_{{1}}^{{\text{T}}} \hat{\boldsymbol{f}}_{1} + \tau_{5} \hat{\boldsymbol{f}}_{2}^{{\text{T}}} \hat{\boldsymbol{f}}_{2} \\ \end{aligned},$$
(64)

where \(\tau_{1} > 0\), \(\tau_{2} > 0\), \(\tau_{3} > 0\), \(\tau_{4} > 0\), and \(\tau_{5} > 0\) are given positive constants. Then, the following main theorem is defined.

Theorem 1: System Eq. (35) with nonlinear exosystem Eq. (36) is considered. Assumptions 1–2 hold. Constants \(\tau_{1} > 0\), \(\tau_{2} > 0\), \(\tau_{3} > 0\), \(\tau_{4} > 0\), and \(\tau_{5} > 0\) exist, matrix \(\boldsymbol{Q}_{1} > 0 \in {\mathbb{R}}^{{n_{x} \times n_{x} }}\), \({\boldsymbol{P}}_{2} > 0 \in {\mathbb{R}}^{{n_{x} \times n_{x} }}\), \({\boldsymbol{X}} \in {\mathbb{R}}^{{n_{x} \times n_{x} }}\) and \({\boldsymbol{Y}} \in {\mathbb{R}}^{{n_{\zeta } \times n_{x} }}\), satisfying the following LMI:

$$\left[ {\begin{array}{*{20}c} {{{\varvec{\Gamma}}}_{1} } & * \\ {0} & {{{\varvec{\Gamma}}}_{2} } \\ \end{array} } \right] < 0,$$
(65)

with

\(\varvec{\Gamma}_{1} = \left[ {\begin{array}{*{20}c} {\boldsymbol{\Xi }_{\boldsymbol{1}} } & * & * & * & * & * & * \\ {\boldsymbol{\Xi }_{\boldsymbol{2}} } & {\boldsymbol{\Xi }_{\boldsymbol{3}} } & * & * & * & * & * \\ 0 & 0 & { - \tau_{1} \boldsymbol{I}} & * & * & * & * \\ {\boldsymbol{F}_{{1}}^{{\text{T}}} } & { - \boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{Y}^{{\text{T}}} } & 0 & { - \tau_{2} \boldsymbol{I}} & * & * & * \\ 0 & {\boldsymbol{F}_{{2}}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & { - \tau_{3} \boldsymbol{I}} & * & * \\ 0 & 0 & { - \boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{Y}^{{\text{T}}} } & 0 & 0 & { - \tau_{4} \boldsymbol{I}} & * \\ 0 & 0 & {\boldsymbol{F}_{{2}}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & 0 & { - \tau_{5} \boldsymbol{I}} \\ \end{array} } \right]\),

\(\varvec{\Gamma}_{2} = \left[ {\begin{array}{*{20}c} {\tau_{1}^{ - 1} \boldsymbol{I}} & * & * & * & * \\ 0 & {\tau_{2}^{ - 1} \boldsymbol{I}} & * & * & * \\ 0 & 0 & {\tau_{3}^{ - 1} \boldsymbol{I}} & * & * \\ 0 & 0 & 0 & {\tau_{4}^{ - 1} \boldsymbol{I}} & * \\ 0 & 0 & 0 & 0 & {\tau_{5}^{ - 1} \boldsymbol{I}} \\ \end{array} } \right]\),

where \(\boldsymbol{\Xi }_{\boldsymbol{1}} = (\boldsymbol{AQ}_{1} + \boldsymbol{B}_{u} \boldsymbol{X}) + *\), \(\boldsymbol{\Xi }_{2} = \boldsymbol{V}^{{\text{T}}} \boldsymbol{B}_{d}^{{\text{T}}}\), \({\boldsymbol{\Xi }}_{3}=\left({{\varvec{P}}}_{2}{\varvec{W}}-{\varvec{Y}}{{\varvec{B}}}_{d}{\varvec{V}}\right)+*\). Then there exists an FDOBC law (Eq. (43)) with FDO (Eqs. (41) and (42)), adaptive update laws (Eqs. (56) and (57)), and DEEO (Eq. (52)), such that the closed-loop system (Eq. (35)) is bounded in the presence of the disturbance of nonlinear exosystem (Eq. (36)). The gain matrices of FDOBC and FDO are given as follows:

$${\boldsymbol{K}} = {\boldsymbol{XQ}}_{1}^{ - 1},$$
(66)
$${\boldsymbol{L}} = {\boldsymbol{P}}_{2}^{ - 1} {\boldsymbol{Y}}.$$
(67)

Proof: Assume that LMI (Eq. (65)) holds for \(\tau_{1} > 0\), \(\tau_{2} > 0\), \(\tau_{3} > 0\), \(\tau_{4} > 0\), \(\tau_{5} > 0\), \({\boldsymbol{Q}}_{1}\), \({\boldsymbol{P}}_{2}\), \({\varvec{X}}\), and \({\boldsymbol{Y}}\). \({\boldsymbol{P}}_{1} = {\boldsymbol{Q}}_{1}^{ - 1}\). Let

$$\tilde{\boldsymbol{P}} = \left[ {\begin{array}{*{20}c} {\boldsymbol{P}_{1} } & 0 \\ 0 & {\boldsymbol{P}_{2} } \\ \end{array} } \right].$$
(68)

By pre- and post-multiplying matrix \({\text{diag}}\left\{ {\boldsymbol{P}_{1} ,\boldsymbol{I},\boldsymbol{I}, \ldots ,\boldsymbol{I},\boldsymbol{I}} \right\}\) using Eq. (65), the following can be derived:

$$\left[ {\begin{array}{*{20}c} \Upsilon & * \\ {0} & {{{\varvec{\Gamma}}}_{2} } \\ \end{array} } \right] < 0,$$
(69)

where \(\Upsilon = \left[ {\begin{array}{*{20}c} {\boldsymbol{\sum }_{1} } & * & * & * & * & * & * \\ {\boldsymbol{\sum }_{2} } & {\boldsymbol{\sum }_{3} } & * & * & * & * & * \\ 0 & 0 & { - \tau_{1} \boldsymbol{I}} & * & * & * & * \\ {\boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{P}_{1} } & { - \boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{Y}^{{\text{T}}} } & 0 & { - \tau_{2} \boldsymbol{I}} & * & * & * \\ 0 & {\boldsymbol{F}_{{2}}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & { - \tau_{3} \boldsymbol{I}} & * & * \\ 0 & 0 & { - \boldsymbol{F}_{{1}}^{{\text{T}}} \boldsymbol{Y}^{{\text{T}}} } & 0 & 0 & { - \tau_{4} \boldsymbol{I}} & * \\ 0 & 0 & {\boldsymbol{F}_{{2}}^{{\text{T}}} \boldsymbol{P}_{2} } & 0 & 0 & 0 & { - \tau_{5} \boldsymbol{I}} \\ \end{array} } \right]\), \(\boldsymbol{\sum }_{1} = \left( {\boldsymbol{P}_{1} \left( {\boldsymbol{A} + \boldsymbol{B}_{u} \boldsymbol{K}} \right)} \right) + *\), \(\boldsymbol{\sum }_{2} = \boldsymbol{V}^{{\text{T}}} \boldsymbol{B}_{d}^{{\text{T}}} \boldsymbol{P}_{1}\), \(\boldsymbol{\sum }_{3} = \left( {\boldsymbol{P}_{2} \boldsymbol{W} - \boldsymbol{P}_{2} \boldsymbol{LB}_{d} \boldsymbol{V}} \right) + *\). Using the Schur complement lemma, the following can be obtained from Eq. (69):

$$\left[ {\begin{array}{*{20}c} {\varvec{\Lambda} }_{1} & 0 \\ 0 & { - \boldsymbol{T}} \\ \end{array} } \right] < 0,$$
(70)

which means that

$${{\varvec{\Lambda}}}_1 \le - {\boldsymbol{T}}.$$
(71)

Then, according to (64),

$$\dot{V} < {\boldsymbol{w}}_{1}^{{\text{T}}} {\boldsymbol{Tw}}_{1}^{{\text{T}}} + \Delta_{e},$$
(72)

where \(\Delta_{e} = \tau_{1} {\boldsymbol{e}}_{\zeta }^{{\text{T}}} + \tau_{2} \Delta {\varvec{f}}_{1}^{{\text{T}}} \Delta {\varvec{f}}_{1} + \tau_{3} \Delta {\varvec{f}}_{2}^{{\text{T}}} \Delta {\varvec{f}}_{2} + \tau_{4} \hat{\boldsymbol{f}}_{1}^{{\text{T}}} \hat{\boldsymbol{f}}_{1} + \tau_{5} \hat{\boldsymbol{f}}_{2}^{{\text{T}}} \hat{\boldsymbol{f}}_{2}\). Because \(\tau_{1}\), \(\tau_{2}\), \(\tau_{3}\), \(\tau_{4}\), and \(\tau_{5}\) are given positive constants, by using Assumptions 1–2 and Eq. (53), \({\Delta }_{e}\) is determined to be bounded. \(\beta ={\lambda }_{\text {min} } \left\{{\varvec{T}}\right\}\) denotes the minimum eigenvalues of matrices. Then, by Eqs. (48) and (72), the following is obtained:

$$\sqrt {\left\| {{{\varvec{\omega}}}_{1} } \right\|^{2} } \ge \frac{{\sqrt {\Delta_{e} } }}{\sqrt \beta }.$$
(73)

It follows that \(\dot{V} \le 0\). Then, for any \(t>{t}_{0},\; \widetilde{{\varvec{x}}}, \; {\widetilde{{\varvec{\theta}}}}_{f_1}\), and \({\widetilde{{\varvec{\theta}}}}_{f_2}\) are all bounded, which means that the state \({\varvec{x}} \left(t\right)\) of the closed-loop system (Eq. (35)) is also bounded.

5 Simulation

In this section, to compare the proposed control method with the traditional PD control method (Wu et al. 2014), the swing angle of the suspended object, the displacement of the actuator, and the control force of different controllers in the presence of the wave force disturbance are demonstrated to confirm the feasibility and robustness of the proposed method.

The simulation mooring-HLC-cargo coupled system parameters are listed in Table 2.

Table 2 Simulation parameters of the system
Full size table

The modellable disturbance system coefficient produced by the wave force exosystem is selected as follows:

  • \({\boldsymbol{V}} = \left[ {\begin{array}{*{20}c} { - 1.5 \times 0.495} & 0 \\ 0 & { - 1.5 \times \left( {0.495} \right)^{2} } \\ \end{array} } \right]\),

  • \({\boldsymbol{W}} = \left[ {\begin{array}{*{20}c} {0.495} & 0 \\ 0 & {0.495} \\ \end{array} } \right]\), \({\boldsymbol{F}}_{2} = \left[ {\begin{array}{*{20}c} {1.5} \\ 2 \\ \end{array} } \right]\),

  • \(f_{2} \left( {{{\varvec{\upzeta}}}\left( t \right)} \right) = \sin \left( {\zeta_{1} (t)} \right)\zeta_{2} (t)\)\({{\varvec{\upzeta}}}\left( 0 \right) = {\hat{\boldsymbol{\zeta }}}\left( 0 \right) = \left[ {\begin{array}{*{20}c} {0.8} & {0.8} \\ \end{array} } \right]\).

The membership functions of FLSs are set as follows:

  • \(\mu_{{F_{i}^{1} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} + 6}}{2}} \right)^{2} } \right]\), \(\mu_{{F_{i}^{2} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} + 4}}{2}} \right)^{2} } \right]\),

  • \(\mu_{{F_{i}^{3} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} + 2}}{2}} \right)^{2} } \right]\), \(\mu_{{F_{i}^{4} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} }}{2}} \right)^{2} } \right]\),

  • \(\mu_{{F_{i}^{5} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} - 2}}{2}} \right)^{2} } \right]\), \(\mu_{{F_{i}^{6} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} - 4}}{2}} \right)^{2} } \right]\),

  • \(\mu_{{F_{i}^{7} }} (x_{i} ) = \exp \left[ { - \left( {\frac{{x_{i} - 6}}{2}} \right)^{2} } \right]\),

and

  • \(\mu_{{F_{i}^{1} }} (\zeta_{i} ) = \exp \left[ { - \left( {\frac{{\zeta_{i} + 4}}{2}} \right)^{2} } \right]\), \(\mu_{{F_{i}^{2} }} (\zeta_{i} ) = \exp \left[ { - \left( {\frac{{\zeta_{i} + 2}}{2}} \right)^{2} } \right]\),

  • \(\mu_{{F_{i}^{3} }} (\zeta_{i} ) = \exp \left[ { - \left( {\frac{{\zeta_{i} }}{2}} \right)^{2} } \right]\), \(\mu_{{F_{i}^{4} }} (\zeta_{i} ) = \exp \left[ { - \left( {\frac{{\zeta_{i} - 2}}{2}} \right)^{2} } \right]\),

  • \(\mu_{{F_{i}^{5} }} (\zeta_{i} ) = \exp \left[ { - \left( {\frac{{\zeta_{i} - 4}}{2}} \right)^{2} } \right]\).

The parameters of the adaptive fuzzy control and the initial state of the parameters are \(\gamma_{1} = 0.3\), \(\gamma_{2} = 0.5\), \({{\varvec{\theta}}}_{1} (0) = 0.1 \times \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]^{{\text{T}}}\) and \({{\varvec{\theta}}}_{2} (0) = 0.1 \times \left[ {\begin{array}{*{20}c} 1 & 1 & 1 & 1 & 1 \\ \end{array} } \right]^{{\text{T}}}\).

By selecting \(\tau_{1} = 0.3\), \(\tau_{2} = 0.2\), \(\tau_{3} = 0.3\), \(\tau_{4} = 0.1\), and \(\tau_{5} = 0.1\) and solving Theorem 1 with the LMI toolbox, the following gain matrices are determined:

  • \(\begin{gathered} {\boldsymbol{K}}\boldsymbol{ = }\left[ {\begin{array}{*{20}c} {2319.9} & {727.5} & 0 & 0 \\ 0 & 0 & {1345.2} & {727.6} \\ \end{array} } \right. \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\begin{array}{*{20}c} { - 33.0} & { - 18.3} & 0 & 0 \\ 0 & 0 & {35.0} & {18.3} \\ \end{array} } \right] \\ \end{gathered}\),

  • \(\begin{gathered} {\boldsymbol{L}} = \left[ {\begin{array}{*{20}c} 0 & {16.20} & 0 & {0.28} \\ 0 & {27.65} & 0 & {0.39} \\ \end{array} } \right. \\ \begin{array}{*{20}c} {} & {} \\ \end{array} \left. {\begin{array}{*{20}c} 0 & {0.56} & 0 & {0.93} \\ 0 & {0.78} & 0 & {0.98} \\ \end{array} } \right] \\ \end{gathered}\).

To prove the stability and anti-disturbance performance of the proposed method, it is compared with the traditional PD control algorithm, where the choice of PD controller is as in Wang et al. (2024a, b).

$$F_{ax} = a\left( {K_{p1} e_{x} (t) + K_{d1} \frac{{\text de_{x} (t)}}{\text dt}} \right) + b\left( {K_{p2} e_{\alpha } (t) + K_{d2} \frac{{\text de_{\alpha } (t)}}{\text dt}} \right),$$
(74)
$$F_{ay} = a\left( {K_{p3} e_{y} (t) + K_{d3} \frac{{\text de_{y} (t)}}{\text dt}} \right) + b\left( {K_{p4} e_{\beta } (t) + K_{d4} \frac{{\text de_{\beta } (t)}}{\text dt}} \right),$$
(75)

where \(e_{x} \left( t \right) = x_{d} - x\), \(e_{y} \left( t \right) = y_{d} - y\), \(e_{\alpha } \left( t \right) = \alpha_{d} - \alpha\), and \(e_{\beta } \left( t \right) = \beta_{d} - \beta\); \(x_{d}\) and \(y_{d}\) are the expected values of the driving strokes; \(\alpha_{d}\) and \(\beta_{d}\) are the expected values of the in-plane and out-of-plane angles, respectively, which are always set as zero. The control parameters of PID are selected as follows:

  • \(K_{p1} = 3300\) , \(K_{d1} = 800\), \(K_{p2} = 2500\), \(K_{d2} = 500\),

  • \(K_{p3} = 200\) , \(K_{d3} = 30\), \(K_{p4} = 100\), \(K_{d4} = 50\).

The simulation results of the driving stroke in the x- and y-directions are presented in Figs. 4 and 5, respectively. The simulation results of the system in-plane angle α are shown in Fig. 6, and the results of the system out-of-plane angle β are shown in Fig. 7. The driving forces in the x- and y-directions are shown in Figs. 8 and 9, respectively.

Fig. 4
figure 4

Driving stroke of x-direction

Full size image
Fig. 5
figure 5

Driving stroke of y-direction

Full size image
Fig. 6
figure 6

In-plane angle α

Full size image
Fig. 7
figure 7

Out-of-plane angle β

Full size image
Fig. 8
figure 8

Driving force in the x-direction

Full size image
Fig. 9
figure 9

Driving force in the x-direction

Full size image

To verify the control effect of the designed control method on the system under different rope lengths, when the cargo mass is m = 100 kg, the displacement of the driving mechanism under l = 15 m, l = 24.85 m, and l = 50 m are selected, and the simulation results are shown in Figs. 10 and 11. To verify the influence of the weight of the suspended object on the swing angle of the suspended object, when the rope length is l = 30 m, the suspended objects with weights of m = 150 kg, m = 100 kg, and m = 50 kg are selected, and the simulation results of the swing angle are shown in Figs. 12 and 13.

Fig. 10
figure 10

Driving stroke of x-direction with different rope lengths

Full size image
Fig. 11
figure 11

Driving stroke of y-direction with different rope lengths

Full size image
Fig. 12
figure 12

In-plane angle α with different cargo mass

Full size image
Fig. 13
figure 13

In-plane angle β with different cargo mass

Full size image

6 Conclusions

In this paper, a new fuzzy swing suppression control strategy is proposed for the mooring-HLC-cargo coupled system with modellable disturbance caused by the exosystem of the wave force. An RBF-based fuzzy approximator is established to approximate the unknown nonlinear functions in the mooring-HLC-cargo system and wave force exosystem. FDO is used to estimate and compensate for external disturbances ascribed to wave force. A DEEO is built to estimate the unknown states in the premise variables. By using FDO, the boundedness of the closed-loop systems is guaranteed. The simulation results validate the effectiveness of the proposed method.

This paper provides a new solution and idea for the swing suppression control of the mooring-HLC-cargo system, but some problems remain unsolved. Future research will focus on the swing suppression control of the suspended object when the rope length changes with time and will further consider the control research of more complex operation actions of the mooring-HLC-cargo system.

In this paper, only the wave force interference is considered. In the future, the influence of multiple interference forces under the actual sea conditions, including wind interference, on the swing of the suspended object will be examined.