1 Introduction

Aerosol particles, which include primary aerosols emitted directly into the atmosphere, precursor gases, and secondary aerosols produced in the atmosphere from various chemically complex solid and liquid particles (Putaud et al., 2010), cause numerous problems in the climate (Lohmann & Feichter, 2005; Ramanathan et al., 2001), human health (Shiraiwa et al., 2012, 2017) and atmospheric chemistry (Andreae & Crutzen, 1997; Bates et al., 1998). For example, aerosol particles in the atmosphere affect ultraviolet ray transmission and the formation of photochemical smog (Castro et al., 2001; Dickerson et al., 1997). Furthermore, the increased proportion of inorganic aerosol particles contributes to air pollution and haze (Che et al., 2019; Huang et al., 2014; Zheng et al., 2015).

Because the chemical properties of aerosols are important, it is necessary to collect the actual aerosol particles and conduct chemical analysis to analyze the chemical properties of aerosol particles. In previous studies, aerosol particles have been collected in various ways to investigate chemical properties. There are two primary methods for collecting aerosol particles: filter sampler (Spindler et al., 2004; Turpin et al., 1994) and cyclone sampler (Zhao et al., 2004; Zhu & Lee, 1999). A filter sampler collects the aerosol particles at a designated flow rate using a vacuum pump. In addition, quartz fiber filters (Wang et al., 2019), polytetrafluoroethylene (PTFE) membrane filters (Nie et al., 2010), polycarbonate membrane filters (Verreault et al., 2010), etc. are used as the materials of filters. In contrast, a cyclone sampler uses centrifugal force to collect aerosol particles (Pan et al., 2021; Willeke et al., 1998). The cyclone sampler generates a centrifugal force on the aerosol particles by rotating the aerosol particles along with the fluid, pushing the aerosol particles out to the wall side. It is collected in the system by gravity dropping it into a space beneath.

With samples of Aerosol particles, previous studies have examined the source (Koulouri et al., 2008) and climate effects of aerosols (Pöschl, 2005), particle size distribution (Espinosa et al., 2001), and microbial distribution in the air (Polymenakou et al., 2008). The chemical component analysis is important in determining the source of aerosol particles and their impact on human society (de Miranda et al., 2017; Koulouri et al., 2008). The methods for analyzing chemical components include Inductively Coupled Plasma Mass Spectrometry (ICP-MS) and X-ray fluorescence (Bernardoni et al., 2011; Chiari et al., 2018; Furger et al., 2017; Mouli et al., 2006; Wang et al., 2006).

Furthermore, understanding the size distribution of aerosol particles is also vital to understand the aerosol properties such as transport velocity (Eck et al., 2020), optical properties (Brock et al., 2019), or deposition of harmful particles in the human lung (Deng et al., 2013; Xing et al., 2016,). Previous studies examined the size distribution of each chemical component of aerosol particles using an electron microscope or impactor (Chen et al., 2016; Huang et al., 2004; Jamhari et al., 2022; Lü et al., 2012; Marple et al., 2014; Mori et al., 2003; Pina et al., 2000; Reid et al., 2003; Wang et al., 2015). In these studies, aerosol particles were collected using a filter sampler and an impactor-based on cut-off particle size. The method expresses the size distribution of each chemical component as a discrete function. Therefore, in previous studies, the resolution of particle size distribution was low. Thus, it has not been possible to thoroughly investigate the exact change in the size distribution of each compound.

In this study, a technique for calculating the particle size distribution of each chemical component in the atmosphere with high size resolution was developed by collecting particles with two types of cyclone samplers and mathematically functionalizing their collection efficiencies as continuous functions. The method developed in this study will be applicable to the investigation of the detailed changes in the chemical properties of the atmosphere in the future.

2 Materials and methods

2.1 Sampling system set-up and evaluation

PM2.5 aerosol particle samples were collected using a large cyclone sampler (HVS3, CS3 Inc., TN, USA; Fig. 1a) and a small cyclone sampler (URG-2000-30EHB, URG, NC, USA; Fig. 1b at 1200 L min−1 and 100 L min−1, respectively. Particles were sampled with the 50% cut-off diameter of 2.5 μm using a real impactor in an amber bottle (I-Chem 100 wide-mouth amber glass jar, 250 mL, Thermo Fisher Scientific Inc., USA) equipped with a cyclone sampler. A backup filter holder equipped with a quartz fiber filter (61–8491-62, Savillex Corporation, Eden Prairie, MN, USA) was connected to the outlet of the cyclone sampler. The quartz filter ensured the sampling of all the particles not captured by the cyclone sampler and allowed clean air to flow through the pump. A mass flow meter (CMS0200BSRN2000D0, Azbil Corporation, Tokyo, Japan), valve (KITZ-02229595, KITZ Corporation, Chiba, Japan), and pump (DA-241S, ULVAC, Inc., Kanagawa, Japan) were connected to control the flow rate during the experiment (Fig. 1). The complete experimental setup is available in Okuda et al. (2015).

Fig. 1
figure 1

Schematic diagram for a the large cyclone sampler, and b the small cyclone sampler

Full size image

The efficiency of the impactor was evaluated by counting the number of particles before and after the impactor with an aerodynamic particle sizer (APS; APS3321 TSI, MN, USA) (Peters et al. 2003). The flow rate was controlled using a mass flow meter (CMS0200BSRN2000D0, Azbil Corporation, Tokyo, Japan). The impactor’s efficiency was determined by comparing the difference between the number of particles of each diameter sampled when the impactor was on and off (six 60 s runs each time).

2.2 Aerosol sampling experiment

The samplers were located on the rooftop of the Yagami campus of Keio University, Yokohama, Japan (35°33′20.1′′N, 139°39′16.0′′E, 30 m above ground level). Sampling was performed using the two cyclone samplers. The flow rates were controlled using mass flow meters and valves. The integrated flow rate was recorded using a mass flow meter. The particle sampling was performed twice: the first was conducted from September 18 to October 14, 2020 (Experiment 1), and the second from January 8 to February 4, 2021 (Experiment 2).

2.3 Chemical analysis of sampled particles

The samples collected from the cyclone samplers (3 mg) were subjected to mass concentration measurements (of Mg, Al, Si, P, S, Cl, K, Ca, Ti, V, Cr, Mn, Fe, Ni, Cu, Zn, and Pb) and inorganic element analysis using X-ray fluorescence EDXRF (EDXL300, Rigaku Corporation, Tokyo, Japan). The primary radiation was emitted from an X-ray tube (50 kV, 1 mA) and the analysis time for each sample was set to 17 min. Fe and Ca were selected as the targeted chemical components among the analyzed chemical components because they are representative crustal elements (Viana et al., 2008).

2.4 Sampling efficiency simulation

To investigate how the differences in the sampling efficiencies of the large and small cyclone samplers resulted in varying chemical compositions of the sampled particles, the mass concentrations of the sampled particles of each particle size were simulated based on the sampling efficiency.

To achieve this, the theoretical mass particle size distribution was assumed to be the lognormal distribution. The lognormal distribution for mass particle size distribution was based on Espenscheid et al. (1964), as shown in Eq. (1).

$$f({d}_{ae})=\frac{\mathrm{exp}\left\{-\frac{{\left(\mathrm{ln}{d}_{ae}-\mathrm{ln}{d}_{m}\right)}^{2}}{2{\mathrm{ln}}^{2}\sigma }\right\}}{\sqrt{2\pi }\mathrm{ln}\sigma {d}_{m}\mathrm{exp}\left(\frac{{\mathit{ln}}^{2}{d}_{m}}{2}\right)}$$
(1)

where \(d_{ae}\) is the aerodynamic diameter of the particle, \({d}_{m}\) is the median aerodynamic diameter of the mass particle, and \(\sigma\) is the standard deviation of the mass particle size.

The penetration rate of the cyclone samplers for each aerodynamic diameter was functionalized by fitting it to a linear line with a singular point. For the small cyclone sampler, the relationship between particle size and sampling efficiency was published on the URG website (URG-2000-30EHB, URG, USA). The small cyclone had a 50% cut-off diameter of 0.12 μm; therefore, the sampling efficiency curve was obtained assuming that the efficiency is the linear line passing through the coordinates of (\(d_{ae}\), \({{P}_{P}}_{cyc}\)) = (0, 1) and (\({d}_{ae}\), \({{P}_{P}}_{cyc}\)) = (0.12, 0.5) where \({{P}_{P}}_{cyc}\) is the penetration ratio of the cyclone samplers. For the large cyclone sampler, evaluated particle size and sampling efficiency were obtained from a previous study (Okuda et al., 2018). Because the large cyclone sampler had a 50% cut-off diameter of 0.18–0.30 μm, the representative 50% cut-off diameter was set as the mean value of the diameter range, 0.24 μm. Thus, the sampling efficiency curve was obtained by connecting (\({d}_{ae}\), \({{P}_{P}}_{cyc}\)) = (0, 1) and (\({d}_{ae}\), \({{P}_{P}}_{cyc}\)) = (0.24, 0.5). As a result of the fitting, the penetration rate of each cyclone sampler was calculated as follows:

$${P_P}_{cyc_{small}}=\left\{\begin{array}{c}-4.17d_{ae}+1if0<d_{ae}\leq\frac1{4.17}\\0\;if\frac1{4.17}<d_{ae}\end{array}\right.$$
(2)
$${P_P}_{cyc_{large}}=\left\{\begin{array}{c}-2.08d_{ae}+1if0<d_{ae}\leq\frac1{2.08}\\0\;if\frac1{2.08}<d_{ae}\end{array}\right.$$
(3)

Hence, the sampling efficiency (\({P}_{S})\) is given as.

$${P}_{s}=1-{{P}_{P}}_{cyc}$$
(4)

The penetration rate of the real impactor was also functionalized as follows:

$${P}_{imp}=1-sig\left({d}_{ae}\right)$$
(5)

where \({P}_{imp}\) is the penetration rate, and \(sig({d}_{ae})\) is the sigmoid function of the aerodynamic diameter, which is given as:

$$sig\left({d}_{ae}\right)=\frac{1}{1+\mathrm{exp}\left(-A\left({d}_{ae}-B\right)\right)}$$
(6)

where \(A\) and \(B\) are coefficients. As a result of the fitting, \(A\) and \(B\) were determined to be 3.60 and 2.13, respectively.

In this simulation, we assumed that the fine particles, such as S, followed particle size distributions with a peak smaller than 2.5 μm and the coarse particles, such as Ca and Fe, followed the particle size distributions with a peak larger than 2.5 μm. Because the EDXRF provides the mass ratio of each chemical component in the particle sample, the ratio of a coarse component to a fine component (Eq. (7)) conveys the chemical characteristics of the sample.

$$\mathrm{r}=\frac{{\int }_{0}^{\infty }{F}_{coarse}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{fine}\mathrm{d}D}$$
(7)

where

$$F({d}_{ae})=f{{({d}_{ae})P}_{P}}_{cyc}{P}_{imp}$$
(8)

Hence, the ratio of fine particle mass concentration to coarse particle mass concentration sampled by the large and small cyclone samplers is given as

$$Ratio=\begin{array}{c}\frac{\left(\frac{{\int }_{0}^{\infty }{F}_{{coarse}_{large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{fine}_{large}}\mathrm{d}D}\right)}{\left(\frac{{\int }_{0}^{\infty }{F}_{{coase}_{small}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{fine}_{small}}\mathrm{d}D}\right)}\\ =\left(\frac{{\int }_{0}^{\infty }{F}_{{coarse}_{large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{coarse}_{small}}\mathrm{d}D}\right)\left(\frac{{\int }_{0}^{\infty }{F}_{{fine}_{small}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{fine}_{large}}\mathrm{d}D}\right)\end{array}$$
(9)

The EDXRF outputs, which are mass ratios of each chemical component, were used to construct a simulation that calculated the mass ratio of S as a fine particle component and those of Fe and Ca as coarse particle components, as the representative examples of the fine particles and the coarse particles, respectively. The reason Fe and Ca were selected was that the sampled mass ratios of particles of these chemical components were the highest in the samples. Therefore, assuming that the mass ratio of coarse particles to fine particles in the experimental samples is the mass ratio of the metal and S components, respectively, the ratio of each chemical component (Fe, Ca) was derived from Eqs. (10)–(11) as follows:

$${Ratio}_{Fe}=\begin{array}{c}\left(\frac{{\int }_{0}^{\infty }{F}_{{Fe}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Fe}_{small}}\mathrm{d}D}\right)\left(\frac{{\int }_{0}^{\infty }{F}_{{S}_{small}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{S}_{large}}\mathrm{d}D}\right)\\ ={C}_{Sul}\left(\frac{{\int }_{0}^{\infty }{F}_{{Fe}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Fe}_{small}}\mathrm{d}D}\right)\end{array}$$
(10)
$${Ratio}_{Ca}=\begin{array}{c}\left(\frac{{\int }_{0}^{\infty }{F}_{{Ca}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Ca}_{small}}\mathrm{d}D}\right)\left(\frac{{\int }_{0}^{\infty }{F}_{{S}_{small}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{S}_{large}}\mathrm{d}D}\right)\\ ={C}_{Sul}\left(\frac{{\int }_{0}^{\infty }{F}_{{Ca}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Ca}_{small}}\mathrm{d}D}\right)\end{array}$$
(11)

Here, because \({\int }_{0}^{\infty }{F}_{{S}_{small}}\mathrm{d}D/{\int }_{0}^{\infty }{F}_{{S}_{large}}\mathrm{d}D\) is common, the mass ratio of the S particles sampled by the small and large cyclone samplers can be replaced by a coefficient, \({C}_{Sul}\). Hence, the difference between the coarse particle sampling efficiencies of the large and small cyclone samplers can be evaluated as a ratio of \({Ratio}_{Fe}\) to \({Ratio}_{Ca}\) as shown in Eq. (12).

$${Ratio}_{coarse}=\begin{array}{c}\frac{{C}_{Sul}\left(\frac{{\int }_{0}^{\infty }{F}_{{Fe}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Fe}_{small}}\mathrm{d}D}\right)}{{C}_{Sul}\left(\frac{{\int }_{0}^{\infty }{F}_{{Ca}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Ca}_{small}}\mathrm{d}D}\right)}\\ =\frac{{\int }_{0}^{\infty }{F}_{{Fe}_{Large}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Ca}_{Large}}\mathrm{d}D}\frac{{\int }_{0}^{\infty }{F}_{{Ca}_{small}}\mathrm{d}D}{{\int }_{0}^{\infty }{F}_{{Fe}_{small}}\mathrm{d}D}\end{array}$$
(12)

The size distributions of the particles of each chemical component in the atmosphere were estimated by setting \({d}_{m}\) and \(\sigma\) in Eq. (1) as the variables.

In addition, \({d}_{m}\) and \(\sigma\) were determined as the atmospheric Ca and Fe particle size distributions when the simulated \({Ratio}_{coarse}\) was reasonably close to the calculated \({Ratio}_{coarse}\) from the EDXRF results.

2.5 Set-up of simulation conditions

To calculate the size distribution of the particles of each chemical component, we assumed that the size distributions of the coarse particles in the atmosphere have the same median diameter (\({d}_{m}\)). Coarse particles are typically 2.5–10 μm in size. Therefore, in this study, the range of 5–7 μm was used as the median diameter of particle size. These values were also validated in previous studies (Horvath et al., 1996; Lough et al., 2005; Lü et al., 2012; Wilson & Suh, 1997). Hence, it was assumed that the Fe and Ca particles in this study had the same median size.

In this study, the median diameter and standard deviation of coarse particles were set as follows:

$${d}_{m}: 5.0, 6.0, 7.0$$
$$\sigma : 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0, 2.1$$

where \(\sigma\) was assumed to be in the range 1.6–2.0 consistent with previous studies (Yu & Luo, 2009). In this study, a sufficiently wider range of \(\sigma\) was selected (1.4–2.1).

The size distributions of Fe and Ca were calculated using Eqs. (10) and (11). The simulations allowed us to specify the range of particle diameters for which a specific value of \(\sigma\) existed. Hence, when \({\sigma }_{1}\) and \({\sigma }_{2}\) were the standard deviations of the size distributions of Ca and Fe, respectively, the sets of variables substituted in Eqs. (10) and (11) in the simulation were as follows:

$$\left({d}_{m}, {\sigma }_{1}, {\sigma }_{21}\right)=\{(5.0, 1.4, 1.4), (5.0, 1.4, 1.5), \dots (5.0, 2.1, 2.1), (6.0, 1.4, 1.4), \dots (7.0, 2.1, 2.1)\}$$

2.6 HYSPLIT model

To evaluate the validity of this analysis result, wind trajectory analysis was also performed in this study to understand the source of the sampling aerosols. A back trajectory analysis using the NOAA Hybrid Single-Particle Lagrangian Integrated Trajectory Model (HYSPLIT; NOAA Air Resources Laboratory, Silver Spring, MD, USA) analysis (Stein et al., 2015) with the ending altitude level of 50 m. The HYSPLIT model was subjected to the following conditions.

Sampling location: 35°33′20.1′′N, 139°39′16.0′′E.

Simulation period: Every day from September 18 to October 14, 2020 (Experiment 1) and from January 8 to February 4, 2021 (Experiment 2) at 0:00 (Japan time) with hourly timestep.

3 Results

Sample information and chemical analysis results.

In Experiment 1, the total mass of the particles sampled from the large and the small cyclone sampler was 170.9 mg and 10.5 mg, respectively, and the total air volumes sampled during the experiments by the large and small cyclone sampler were 45,749 m3 and 3716 m3, respectively. In Experiment 2, the total mass of the particles sampled from the large and the small cyclone sampler was 241.9 mg and 57.2, respectively, and the total air volumes sampled during the experiments by the large and small cyclone sampler were 47,105 m3 and 3969 m3, respectively (Table 1).

Table 1 Information on samples sampled by cyclone sampler
Full size table

The mass ratios of S, Fe, and Ca were calculated excluding Al because the small cyclone sampler was made of Al. From the EDXRF analysis, the mass ratios of S, Fe, and Ca sampled by the large cyclone sampler during Experiment 1 were 26.83%, 3.21%, and 9.16%, respectively; and that by the small cyclone sampler were 68.58%, 2.30%, and 2.92%, respectively. In Experiment 2, the mass ratios of S, Fe, and Ca sampled by the large cyclone sampler were 6.68%, 4.01%, and 13.96%, respectively; and that by the small cyclone sampler were 62.40%, 2.80%, and 2.63%, respectively (Table 2).

Table 2 Results of EDXRF and mass percentages of each component (values in parentheses indicate mass percentages when aluminum is included)
Full size table

The calculated \({\mathrm{Ratio}}_{\mathrm{coarse}}\) from the EDXRF results were 2.25 (Experiment 1) and 3.71 (Experiment 2).

3.1 Simulation results

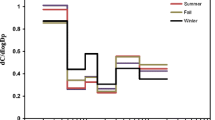
The simulation results (Fig. 2) revealed that the simulated \({\mathrm{Ratio}}_{\mathrm{coarse}}\) was the largest when the standard deviation of the size distribution of Ca (\({\sigma }_{1}\)) was the smallest and that of Fe (\({\sigma }_{2}\)) was the largest, regardless of the amplitudes of the \({d}_{m}\). In addition, the \({Ratio}_{coarse}\) increased with increasing \({d}_{m}\). Moreover, particle size distributions in Experiments 1 and 2 are different. In Experiment 2, the distribution of Fe was wider than that in Experiment 1. Additionally, the larger the \({d}_{m}\), the smaller the change in particle size distribution in both experiments.

Fig. 2
figure 2

Simulated relationship between the \({\mathrm{Ratio}}_{\mathrm{coarse}}\) and the standard deviations of the size distributions of Ca (\({\sigma }_{1}\)) and Fe (\({\sigma }_{2}\))

Full size image

As a result of the simulation, a possible relationship between the coarse particle median diameter and the standard deviations of airborne Fe and Ca particles was derived when the median diameter was set in the range of 5–7 m (Table 3). The possible size distributions of Fe had a higher peak value at the median diameter in experiment 1 (Figs. 3 and 4).

Table 3 List of possible standard deviations of the size distributions of Ca (\({\sigma }_{1}\)) and Fe (\({\sigma }_{2}\)) at each \({\mathrm{Ratio}}_{\mathrm{coarse}}\) (2.25 and 3.71)
Full size table
Fig. 3
figure 3

Simulated possible size distributions of Fe and Ca airborne particles during Experiment 1

Full size image
Fig. 4
figure 4

Simulated possible size distributions of Fe and Ca airborne particles during Experiment 2

Full size image

4 Discussion

Aerosol particles in the atmosphere can affect climate change and human health. Thus, it is necessary to estimate the distribution of each chemical component. These findings may also aid in understanding the impact of atmospheric aerosol particles on the earth and environment.

As shown in Table 2, the aerosol chemical composition was different for the two samples. To solve this problem mathematically, the value of either \(\sigma\) or \({d}_{m}\) has to be fixed. These two variables may not be determined exclusively because of strong assumptions, such as coarse particle distributions always having the same median diameter or standard deviation. However, when the particle size of the coarse particles follows a normal distribution, the size distributions of Fe and Ca are expected to have almost the same size distributions as those calculated in this study.

Experiments 1 and 2 were conducted at the same sampling sites. However, the sampling period and size distribution of each chemical component differed. On comparing the results of Experiment 1 and Experiment 2, the peak of the size distributions showed peak shifts when the standard deviations of Fe and Ca were set to similar values (\({\sigma }_{1}\):1. 4, \({\sigma }_{2}\): 1.8–1.9; Figs. 3a and 4d). In previous studies (Hussein et al., 2004; Wu et al., 2008), it was discovered that particle size distribution varied following the period or season, which could be due to the increase in the number of fine particles in winter (de Miranda et al., 2002). Our HYSPLIT simulation revealed that the air parcel arrived at the sampling site from the Pacific Ocean (Northeast) in September, while it arrived from northwest Japan in January (Fig. 5). Sea salt particles are expected to dominate wind blowing from the ocean, resulting in a decrease in median particle diameter. In our simulation, the estimated distribution of coarse Fe particles has increased since the winds originated on the mainland in January. These findings support previous findings (Maring et al., 2003; Porter & Clarke, 1997) that sea salt particles have a smaller particle diameter than mineral particles.

Fig. 5
figure 5

Results obtained from the HYSPLIT model. The trajectories of the air parcel during Experiment 1 are represented by the blue lines, and Experiment 2 are represented by the red lines

Full size image

Some studies have focused on calculating particle size distribution using a discrete function, which can roughly predict the particle size distribution of the chemical components. However, in this study, size distribution was presented as a continuous function. The resolution of a continuous function is higher than that of the discrete distribution, meaning slight differences can be precisely recognized. In addition, the particle size distribution of the chemical composition of indoor air can be determined using atmospheric and indoor sampling (Parker et al., 2008). Hence, it seemed more practical to employ a continuous function to determine the particle size distribution of the chemical composition rather than a discrete distribution.

Aerosol particles were sampled for a month in each experimental duration in this study, and this long duration of sampling was possibly influenced by various sources. Thus, future studies should use shorter sampling periods to precisely identify the particle sources and analyze the relationship between the changes in size distribution and seasonal sources. Additionally, to ensure that the simulation method developed in this study can track the seasonal changes in particle size distributions of each chemical component, it is necessary to sample the airborne particles using both the cyclone and filter samplers simultaneously. Although Fe particles exist in the fine mode in the atmosphere (Gao et al., 2019), these particles were not considered in this analysis because of the generality of the Fe particle size properties. However, even if Fe exists in fine mode, our study is expected to be able to evaluate the peak shift caused by the Fe particles in the fine mode to some extent. Finally, although only particle size distributions of Ca and Fe were the focus of this study, it is necessary to examine the particle size distribution of different chemical components and compositions to deepen our understanding of the chemical properties of the atmosphere.

In future studies, the evaluations of the size distributions of other chemical aerosol particles such as Cr, Zn, or Pb, which strongly relevant to the human health, are required. In addition, it is necessary to measure the actual aerosol size distribution using an Anderson cascade impactor in parallel and evaluate if the sampling results agree with the simulation results to validate our theory. Additionally, studying the daily-scale relationship between the meteorological parameters and the size distributions is also required to fully understand the dynamics of the aerosol particles.

5 Conclusion

In addition, using the data from the EDXRF analysis of the samples obtained from the impactor and cyclone sampler, the particle size distributions of each chemical component could be calculated as continuous functions. Our findings revealed that the difference in the particle size distribution of each chemical component of aerosol particles in the atmosphere sampled over different periods can be more accurately investigated than in previous studies. Furthermore, the simulation was able to provide a finite number of size distribution candidates. When the standard deviations of the size distributions were assumed to be constant regardless of the seasonal changes, our method decisively shows the seasonal change in the median diameter, which does not contradict previous studies. Future studies should focus on shorter sampling periods using both cyclone and filter samplers to accurately simulate particle size distribution of different chemical components and compositions in the atmosphere. In addition, it is believed that the application of chemical components that may have health effects, such as heavy metals, should be fully considered.