1 Introduction

Wind tunnel bench tests of aerodynamic models intended for fixed- and rotary-wing applications such as in traditional aircraft or wind turbine in energy industry can contribute to elucidate important aspects of the aeroelastic behavior of a structure subjected to different airflow conditions and complement theoretical and numerical findings. The manifestation of self-sustained, bending-torsion coupled oscillations, for example, is typically observed at sufficiently high airflow speed (or dynamic pressure), and the structure may respond differently depending on the combination of mechanical and aerodynamic characteristics [1,2,3,4,5].

While linear models provide useful insights into the general aeroelastic behavior of the structure in terms of critical speed for the onset of unstable flutter oscillations, nonlinear models capture specific features in post-flutter conditions (above the linear flutter speed), when linear behavior is overwhelmed by nonlinear effects of structural and aerodynamic natures. Examples of such oscillatory phenomena are encountered in highly flexible large aspect-ratio wings, rotating wings of wind turbines and helicopter rotors, turbo-machinery blades, and other structures not necessarily related to the aerospace field (cable-stayed bridges, buildings, oil risers etc.) [2, 3, 6,7,8,9,10,11].

When significant flow direction variations occur, large angles of attack (stall) can trigger massive vortex shedding. The associated pressure fluctuations create aerodynamic imbalances around the structure and lead to additional pitching moments of aerodynamic nature. The interaction with inertial and elastic moments promotes the onset of stall-induced structural oscillations [12,13,14]. The manifestation of such oscillations is experimentally and numerically addressed in recent studies. The two-dimensional airfoil models and finite elastic wings in general wind tunnel contexts of basic research and in application-specific contexts such as in helicopter rotors and wind turbine blades are considered [9,10,11, 15,16,17,18,19,20,21].

Important works address the aeroelastic behavior of structurally nonlinear models, where the source of nonlinearity is the stiffness freeplay, bilinear or polynomial stiffness, or combinations of them [2]. Remarkable ones focus on the aeroelastic behavior of pitch-and-plunge airfoil (PAPA) models with trailing-edge control surface freeplay [22,23,24]. Geometrically nonlinear aeroelastic models subjected to large deformation are also considered [3, 25, 26]. The Pazy wing is being established as a benchmark model for the investigation of nonlinear aeroelastic effects in wing dynamics [6, 7]. The linearized system eigenvalues of a coupled state-space solution of unsteady vortex lattice method and structural model in modal domain show the flutter characteristics change considerably with increasing wing deflection [6]. In agreement, model predictions with nonlinear kinematics show the flutter onset is significantly affected by curvature effects as the wing static deflection increases, but it is reported that such effect (related to a reduction in the wing torsional natural frequencies) is not properly captured by linear kinematics [7].

The stable nature of the nonlinear oscillations for a certain range of airflow speeds is also attractive in energy harvesting, where the harvested electrical power could supply wireless sensors and actuators. Many works focus on enhancement strategies for airflow-based energy harvesting [27,28,29,30,31,32]. A mechanism based on the pseudoelastic hysteresis of superelastic shape-memory alloy (SMA) elements is numerically investigated in [33]. The mechanism is experimentally demonstrated by wind tunnel tests of a PAPA model with SMA helical springs in [34, 35] (the energy harvesting feature is not considered in the experiment). Other works focus on the aerodynamically nonlinear behavior of PAPA models in aeroelastic and electroaeroelastic cases [15,16,17,18,19]. The latter has examples with piezoelectric and electromagnetic mechanisms, promoting attractive configurations with relatively wide operating envelopes above the linear flutter speed of the aeroelastic system.

In this study, a typical PAPA model is considered to experimentally investigate nonlinear post-flutter oscillations of the airfoil in wind tunnel bench tests for a range of airflow speeds. Relatively low speeds are considered in the tests, achieving values not greater than 10 m\({\cdot }\mathrm{{s}}^{-1}\) (Mach numbers below 0.05), with Reynolds numbers on the order of 1.5\(\times\)10\(^5\). A brief theory review is presented with fundamental concepts, followed by a description of the wind tunnel setup and the report of the experimental results. The aeroelastic behavior is discussed specially for the range of airflow speeds where stable nonlinear post-flutter limit-cycle oscillations (LCOs) are observed. This work is, therefore, a contribution to a broader research effort related to experimental and numerical investigations of aeroelastic models (intended for wind energy applications) undergoing nonlinear oscillations of different natures, possibly combining LCOs of structural origin and LCOs of aerodynamic origin. In the particular work described in this paper, however, effort is dedicated to avoid structurally nonlinear effects, while the nonlinear aerodynamic effects may be related to large pitching angles (dynamic stall) as well as to effects of low Reynolds numbers and viscous separation bubbles at small pitching angles. Possible future studies may involve numerical simulations of structurally and aerodynamically nonlinear models and wind tunnel tests of improved rigid and flexible aeroelastic prototypes.

2 Brief theory review

The experimental apparatus and wind tunnel tests that are presented later (Sects. 3 and 4) are based on consolidated concepts from the literature on Aeroelasticity. The airfoil model is presented first along with its equations of motion (although no numerical solution of the equations is presented, they are useful to support discussions concerned with the airfoil behavior and pertinent model parameters). The general airfoil behavior is then briefly reviewed for linear and nonlinear cases to illustrate what is experimentally pursued in Sect. 4.

2.1 Pitch-and-plunge-airfoil model

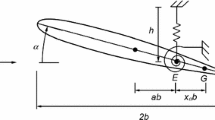
A classical PAPA model schematics is shown in Fig. 1 [1]. The pitch and plunge structural displacements are denoted by \(\theta\) and h, respectively (positive as indicated in the figure). The span-normalized, two dimensional, aeroelastic parameters are the airfoil mass (\(m_\theta\) and \(m_h\) for the rotational and translational motions, which are typically different in experimental setups), moment of inertia about the elastic center (\(I_\theta\)), plunge spring stiffness (\(k_h\)), torsional pitch spring stiffness (\(k_\theta\)), and damping ratios (\(\zeta _h\) and \(\zeta _\theta\)), all of them expressed as per unit span. The pertinent airfoil lengths and locations are the span length (l), chord (c) and semichord (\(b = c / 2\)), center of gravity (CG), elastic center (e.c., \(x_{\mathrm{{ec}}}\)), CG – \(x_{\mathrm{{ec}}}\) offset (\(x_\theta\), in semichords), and the aerodynamic center (a.c., \(x_{\mathrm{{ac}}}\)). The relative wind (from the wind tunnel) is represented by \(V_\infty\). A visual representation of the airfoil motion over time is shown in Fig. 2.

Fig. 1
figure 1

Schematics of a pitch-and-plunge-airfoil (PAPA) model under airflow excitation. The aerodynamic center is indicated by a.c., the elastic center by e.c., and the center of gravity by C.G

Full size image
Fig. 2
figure 2

Visual representation of the coupled airfoil motion. The curve in blue represents the plunge (translational) displacement and the curve in red represents the pitch (angular) displacement. This figure is available as supplementary material in animated form

Full size image

The unsteady aerodynamic loading (per unit span) is represented by lift (L), defined as a lumped force perpendicular to \(V_\infty\) acting at the aerodynamic center, and by aerodynamic moment (M) acting around the elastic center. The aerodynamic moment may have contributions from the lift acting through a moment arm, from aerodynamic loading distributions in dissymmetry between the upper and lower airfoil surfaces that result in moment due to forces acting at distinct locations in opposite directions (denoted by \(M_{\mathrm{{ac}}}\)), and from nonlinear aerodynamic phenomena with pressure fluctuations related to massive vortex shedding near the airfoil leading edge [1, 12, 13]. The aerodynamically nonlinear behavior is of particular interest in this study and is experimentally addressed based on wind tunnel bench tests of an airfoil prototype that corresponds to the schematic in Fig. 1.

The coupled governing equations of the airfoil section are obtained from the classical Lagrange approach [1] and presented in the consolidated Theodorsen’s dimensionless form [36],

$$\begin{aligned} \begin{array}{l} {\mu _e}\ddot{{\bar{h}}} + {x_\theta }\ddot{\theta }+ {\zeta _{h}}\dot{{\bar{h}}} + \omega _h^2 {{\bar{h}}} = - L \\ r_\theta ^2\ddot{\theta }+ {x_\theta }\ddot{{\bar{h}}} + {\zeta _{\theta }}{{\dot{\theta }}} + r_\theta ^2\omega _\theta ^2\theta = M \end{array}, \end{aligned}$$
(1)

with viscous damping and aerodynamic loading included, where \({\bar{h}} = h/b\) is the plunge displacement in semichords, \(\mu _e\) is the plunge-to-pitch mass ratio (possibly unity in numerical studies and typically larger than unity in experimental cases), \(r_\theta\) is the radius of gyration per semichord, \(\omega _{\left( \right) }\) are frequency-related parameters from the nondimensionalization process (not necessarily equal to the physical natural frequencies), and \(\zeta _{\left( \right) }\) are damping ratios. The unsteady aerodynamic loading (per unit span) is given by the time-dependent lift \(L = \kappa {c_l}\) and moment \(M = 2\kappa c_{m_{\mathrm{{ec}}}}\), where \(\kappa = {{{{V_\infty }^2}} {/} {(\mu \pi {b^2})}}\),

and \(\mu\) is the air mass ratio. In the traditional Theodorsen’s form, the lift (force) equation is divided by mb, while the pitching (moment) equation is divided by \(m b ^2\). With some manipulation and symbol substitutions (defined in [36]), Eq. 1 is obtained. In addition, the airflow speed symbol \(V_\infty\) will be redefined according with the context to denote specific critical speeds (in linear and nonlinear cases), and is eventually expressed in the “reduced” dimensionless form \(u = V / { ( \omega b ) }\) for convenience.

The lift coefficient \(c_{l}\) and moment coefficient \(c_{m_{\mathrm{{ec}}}}\) may be determined by the implementation of many different aerodynamic models, depending on the purpose of the study. Unsteady and nonlinear models would be preferred to numerically investigate the experimental problem addressed in this study due to the complex vortex-shedding mechanisms involved [1, 12, 13, 20].

2.2 Typical aeroelastic behavior of the airfoil

Figure 3 depicts a typical aeroelastic behavior for the airfoil (of Fig. 1) in linear and nonlinear responses at different airflow speeds. The specific critical flutter speed (\(V_{LF}\)) is indicated for the linear case and corresponds to the (dynamical system) neutral stability boundary, where the steady-state oscillations theoretically exhibit constant amplitudes. At airflow speeds larger than \(V_{LF}\) the oscillation amplitudes grow over time theoretically to infinite, but in practice can be bounded after some transient growth by structural and aerodynamic nonlinear effects. In such a case, the steady-state amplitudes increase with increasing airflow speeds for a certain range of airflow speeds. The pair of cut-in and cut-out critical airflow speeds, respectively for the appearing and disappearing of stable self-sustained oscillations, is also indicated for the nonlinear case (\(V_{\mathrm{{cut-in}}}\) and \(V_{\mathrm{{cut-out}}}\)). At airflow speeds above \(V_{\mathrm{{cut-out}}}\) the airfoil response is dynamically unstable, in a situation where the oscillations are massively large from the structural point of view and could damage the apparatus if not controlled. The airfoil behavior at airflow speeds within the stable envelope is of particular interest in this study and is experimentally pursued later in Sect. 4.

Fig. 3
figure 3

Typical airfoil response in linear and nonlinear cases at different airflow speeds. The region with stable LCOs is the focus of this study, and \(V_{\mathrm{{cut-in}}} \approx V_{LF}\) in the particular experimental configuration considered, as demonstrated in Sect. 4 (Results). (LCO: limit-cycle oscillation)

Full size image

3 Experimental setup

The experimental setup is described in this section. The airfoil design and construction is described first, followed by the identification of its aeroelastic parameters.

3.1 Airfoil model design and construction

The widely consolidated spring-assisted rigid airfoil configuration is considered, where steel springs provide stiffness to the pitch and plunge degrees of freedom (DoFs) of the aeroelastic model [16, 22, 24, 28, 34, 37]. This benchmark model exhibits important behaviors of elastic wings and blades with bending-torsion coupled vibration modes. A styrofoam NACA0012 profile was produced by a CNC-like hot-wire cutting machine oriented by G-code. The concept design and construction process of the experimental apparatus is shown in Fig. 4.

Fig. 4
figure 4

Airfoil model design and construction. a Schematic drawing of the airfoil associated with the stationary frame to be fixed in front of the wind tunnel. b Construction of the supporting apparatus showing the axis of rotation coupled to bearings and the steel beam springs to allow translational motion. c Construction of the styrofoam airfoil prototype (bonded to the rotation axis) and detail of the spring wire torsional stiffness mechanism. d Complete airfoil prototype

Full size image

Two pairs of steel beam springs confer translational restoring forces to the plunge DoF and a stainless steel spring wire confers torsional stiffness to the pitch DoF. An aluminum circular bar passes along the span direction of the airfoil at the point of one quarter of the airfoil chord length and is associated with the plunge DoF via ball bearings to allow the rotational motion of the airfoil (the location of the bar is the elastic center of the model). The pitch DoF spring wire passes through the aluminum bar in the radial direction to create elastic restoring moment proportional to the angular displacement of the airfoil (the ends of the spring wire are supported in the metal plates where the bearings and beam springs are fixed). For preliminary design purposes, the stiffness parameters may be estimated from classical strength of materials theory. The effective parameters, however, are experimentally identified in Sect. 3.2.

While the aluminum bar position is a project decision, it is intentionally placed at the aerodynamic center of the airfoil to avoid the manifestation of the static divergence phenomenon. It may be verified by simple inspection of the static moment equilibrium equation for the airfoil that the critical divergence dynamic pressure (and corresponding airflow speed) equals infinity in such a particular case [1]. The airfoil CG, on the other hand, is intentionally aft the elastic center since flutter-like phenomena are strongly related to the inertial coupling between the model degrees of freedom. For this purpose, a small mass is placed near the trailing edge of the airfoil to offset the CG aft (through the unfilled spaces in the airfoil body that can be seen in the picture). With an estimation of the pitch and plunge stiffness parameters along with sufficiently aft CG, the onset of self-sustained aeroelastic oscillations is expected within the operation envelope of the available wind tunnel (as confirmed in Sect. 4).

3.2 Experimental estimation of the airfoil structural parameters

The airfoil structural parameters are presented in this section. A number of parameters, such as mass and characteristic distances, may be promptly measured, while other parameters (moment of inertia, damping and stiffness) require some additional treatment for their estimation. Concerning with the directly measured properties, the total span length of the airfoil is 0.60 m, while the span length effectively exposed to the wind tunnel airflow is 0.50 m. The airfoil chord length is 0.25 m (semichord length of 0.125 m). The mass of the apparatus restricted to rotation only is 0.49 kg and the mass in translational motion is 2.34 kg. The distance between the center of rotation and the CG is 0.040 m. The estimation of the remaining properties is described next.

Figure 5 depicts the test for the estimation of the airfoil moment of inertia around its center of rotation in a pendulum configuration. The moment of inertia \(I_\theta\) = 0.00261 kg\(\cdot\)m\(^2\) was determined from the pendulum equation, \(T_\theta = 2 \pi \sqrt{ I _\theta / \left( m g d \right) }\), based on the observed period of oscillation \(T_\theta\) = 0.733 s, and on the previously known airfoil mass in rotation, CG-rotation axis offset, and local acceleration of gravity (g = 9.788 m\(\cdot\)s\(^{-2}\)).

Fig. 5
figure 5

Airfoil free rotation test in pendulum configuration to determine its moment of inertia around the pitch axis (\(I_{\theta }\)). a Airfoil in pendulum configuration (without the torsional spring). b Angular motion of the airfoil captured by a free object-tracking software [38]. c Airfoil pendulum oscillation time history

Full size image

A free object-tracking software [38] was employed along with a conventional digital camera to record the airfoil motion during the estimation of the moment of inertia. The tracking software was also employed during the estimation of the stiffness and damping parameters, and during the wind tunnel tests to capture both the pitch and plunge displacements. In the latter, by following two distinct points of reference in the airfoil tip (at the end of the aluminum bar for the plunge motion and at a specific point near the trailing edge of the airfoil for the pitch motion). A sampling rate of 240 data points per second was assumed.

The pitch and plunge stiffness parameters (in physical units) were identified as 0.414 N\(\cdot\)m\(\cdot\)rad\(^{-1}\) and 952 N\(\cdot\)m\(^{-1}\), respectively, based on the uncoupled damped frequency of oscillation (restricted to 1-DoF in each case) during free vibration tests at zero airflow speed. It may be worth recalling the plunge frequency in the dimensionless equations of motion of the airfoil involves the rotation mass (not the translational mass) due to the nondimensionalization process and has different value from the actual oscillation frequency. The pitch and plunge damping ratios were identified as 0.113 and 0.016, respectively, based on the logarithmic decrement method. The results of the free vibration tests are shown in Fig. 6, revealing significant damping in pitch and slightly damped plunge motion (in agreement with other reports of similar models from the literature [22, 28, 34]). The airfoil parameters are summarized in Table 1 in dimensional form (normalized by the airfoil span length) and in Table 2 in dimensionless form (as in Eq. 1).

Fig. 6
figure 6

Airfoil pitch and plunge uncoupled free vibration tests for the estimation of stiffness and damping parameters

Full size image
Table 1 Dimensional airfoil parameters (inertial, damping and stiffness parameters are normalized by the span length (l); \({\bar{\omega }}_{\left( \right) }\) represents the experimental uncoupled natural frequencies)
Full size table
Table 2 Dimensionless airfoil parameters (\(\omega _{h} = \sqrt{(}k_h / {m_\theta })\) is a frequency value from the nondimensionalization process of the equations of motion (Eq. 1) and involves the pitch mass). The characteristic lengths correspond to fractions of the airfoil semichord
Full size table

Figure 7 shows the wind tunnel setup used in the bench tests along with the PAPA model. The wind tunnel has a maximum airflow speed of about 19 m\({\cdot }\mathrm{{s}}^{-1}\) and a square test section of 0.5 m \(\times\) 0.5 m in the open-jet configuration used in this work. The wind tunnel is equipped with conventional Pitot tube and pressure sensors for indication of the airflow speed. The wind tunnel is installed in the Laboratory of Aeronautics of the Sao Paulo State University, Campus of Sao Joao da Boa Vista (Brazil), and is exposed to the local ambient condition. The year-round average temperature and air pressure are 21\(^\circ\) C and 926 hPa (0.914 atm), respectively. The corresponding air density is 1.090 kg\({\cdot }\)m\(^{-3}\), below the average value of 1.225 kg\({\cdot }\)m\(^{-3}\) from the International Standard Atmosphere (ISA). The onset of self-sustained oscillations is, therefore, expected to take place at a slightly higher airflow speed than that for the ISA average density.

Fig. 7
figure 7

Pictures of the experimental apparatus mounted in the Laboratory of Aeronautics of the Sao Paulo State University. Side view of the open-jet wind tunnel (a). Pitch-and-plunge airfoil prototype exposed to the airflow (b)

Full size image

3.3 Estimation of the airfoil aerodynamic characteristics

Although this study is focused on the experimental approach, the airfoil aerodynamic parameters are important in other studies where the representation of unsteady and nonlinear aerodynamic forces and moments requires the numerical solution of aerodynamic models such as the Beddoes-Leishman, for example, and it is obvious that more representative airfoil parameters would be preferred in the simulations, rather than assuming literature parameters despite different airflow conditions. For this purpose, the widely employed Xfoil solver, a free software developed by Mark Drela and Harold Youngren for viscous and inviscid analysis of airfoils in subsonic flows [39], is used to estimate general airfoil aerodynamic characteristics. The lift-curve slope and stall angle of attack are particularly important, and pressure distribution information is included for completeness.

For our specific airfoil profile, dimensions, and flow conditions, the kinematic viscosity is about 1.51\(\times\)10\(^{-5}\) m\(^{2}{\cdot }\)s\(^{-1}\) and the Reynolds number is on the order of 1.5\(\times\)10\(^{5}\) (a relatively low value). Figure 8 shows the aerodynamic coefficients for lift, drag and moment, for Reynolds numbers of 1.0\(\times\)10\(^{5}\) and 2.0\(\times\)10\(^{5}\), a range of values wide enough for the tests conducted during this study. The Xfoil calculations consider a parameter (\(n_{\mathrm{{crit}}}\)) to represent airfoil skin roughness and trigger fluid transition to turbulence, suggesting the values 4 to 8 for non-smooth (“dirty”) wind tunnel flows, 9 for an average wind tunnel, and 10 to 12 for smooth (“clean”) wind tunnel flows. The available wind tunnel is considered as an average one and the airfoil is made of styrofoam with a plastic coverage, such that curves for \(n_{\mathrm{{crit}}}\) equal to 5 and 9 are shown to represent a wide range of airflow smoothness conditions.

Fig. 8
figure 8

General airfoil profile (two dimensional) aerodynamic characteristics of lift, drag and moment (in coefficient form). Lift coefficient a, drag coefficient (b), lift-to-drag ratio (c), pitching moment coefficient d. All curves in the graphs (b–d) correspond to the same flow characteristics (Reynolds number and n parameter) described in the legend of graph (a)

Full size image

The curves in Fig. 8 illustrate how the lift production becomes closer to linear at smaller angles of attack (reducing low Reynolds effects) and the critical stall angle increases for increasing Reynolds numbers. The corresponding \(c_{l} \times \alpha\) curve slope predicted for the linear regime is 5.25 rad\(^{-1}\) (or 0.092 per degree), about 15% smaller than the theoretical value of 2\(\pi\) rad\(^{-1}\) predicted from the thin airfoil theory. The predicted stall angle is also smaller at lower Reynolds numbers, as expected. For the particular case of this study, the stall angle is in the range between 10\(^\circ\) and 12\(^\circ\), while some works from the literature consider larger stall angles for the same airfoil profile (with values of about 15\(^\circ\), which are more suitable for larger Reynolds numbers).

The airfoil pressure distribution at different angles of attack is depicted in Fig. 9. The pressure coefficient graphs are reversed in the y-direction for more straightforward correspondence of the upper and lower airfoil surfaces with the curves in the graphs, as usual, and local pressure values greater than the free stream pressure far ahead of the airfoil are indicated by normal arrows pointing inwards the airfoil (and lesser pressure values by outwards arrows). For the interested reader, a detailed discussion on this subject is presented in [14] based on experimental studies (includes comparison with the Xfoil solution in some cases) and is extended for unsteady cases. Moreover, to support discussions presented later (in Sect. 4), Fig. 10 shows pressure graphs considering viscous effects to depict the effect of separation bubbles. With increasing angle of attack, the effect on the pressure distribution becomes more significant and the point of bubble formation displaces towards the leading edge of the airfoil.

Fig. 9
figure 9

Airfoil pressure distribution at different values of angle of attack (0\(^\circ\), 4\(^\circ\), 8\(^\circ\) and 12\(^\circ\)), represented in coefficient form and with visual representation (Re = 10\(^{5}\)). Graphs with reversed \(c_p\) axis for convenience such that lower and upper curves and airfoil surfaces correspond with each other. Arrows pointing inwards the airfoil represent local pressure greater than the free stream reference pressure (positive pressure coefficient values), and outwards arrows indicate local pressure smaller than the reference value (negative coefficient values)

Full size image
Fig. 10
figure 10

Airfoil pressure distribution at 4\(^\circ\) and 8\(^\circ\) of angle of attack when viscous effects are considered (Re = 10\(^{5}\))

Full size image

4 Results

This section presents the results of the airfoil wind tunnel bench tests conducted at different airflow speeds. The results are first presented in time-domain, followed by a description in other formats typically convenient in aeroelastic analysis to highlight the frequency and amplitude of oscillation dependence with the airflow speed in post-flutter regime.

4.1 Time-domain airfoil response in wind tunnel tests

The airfoil was tested in the wind tunnel for increasing airflow speeds by applying arbitrary (small) initial displacements and observing the aeroelastic response over time. Theoretically, the critical flutter speed is determined when the linear system is marginally stable and its value is independent of the applied initial condition. An experimental investigation, however, possesses imperfections and eventually exhibits nonlinear responses such as the onset of self-sustained oscillations slightly below the expected speed for large enough initial condition (hard flutter).

The possibility of encountering hard flutter was investigated by slightly decreasing the airflow speed after self-sustained oscillations were first observed and repeating the test for increasing initial conditions, but did not manifest in the tests, as shown in Fig. 11 for the airflow speed of 7 m\({\cdot }\mathrm{{s}}^{-1}\) (reduced speed of 4.4). The airflow speed was increased again and the tests proceeded in search for the more interesting post-flutter oscillations.

Fig. 11
figure 11

Hard flutter verification test with large initial condition at slightly below the cut-in airflow speed (not observed). Pitch and plunge time responses are shown for the airflow speed of 7 m\({\cdot }\mathrm{{s}}^{-1}\) (reduced speed of 4.4)

Full size image

Figure 12 displays the aeroelastic displacements of the airfoil over time for a range of increasing airflow speeds. Stable LCOs are observed for airflow speeds between the cut-in and cut-out critical values of about 8.1 m\({\cdot }\mathrm{{s}}^{-1}\) (reduced speed of 5.1) and 9.5 m\({\cdot }\mathrm{{s}}^{-1}\) (reduced speed of 6.0), respectively. In the vicinity of the critical lower and upper speed values the response is marginally stable and eventually affected by secondary factors such as ambient temperature variations and model imperfections inherently to the construction process.

Fig. 12
figure 12

Stable LCOs observed for airflow speeds between the cut-in and cut-out critical values. Airflow speeds of 8.1 m\({\cdot }\mathrm{{s}}^{-1}\) a, 8.4 m\({\cdot }\mathrm{{s}}^{-1}\) b, 9.0 m\({\cdot }\mathrm{{s}}^{-1}\) c, and 9.5 m\({\cdot }\mathrm{{s}}^{-1}\) d (reduced speed values of 5.1, 5.3, 5.7 and 6.0). (LCO: limit-cycle oscillation)

Full size image

At airflow speeds below 9.0 m\({\cdot }\mathrm{{s}}^{-1}\), the nonlinear response is attributed to aerodynamic effects not necessarily related to the critical stall angle being exceeded, but also to low Reynolds number effects (affecting the linearity of the lift-curve slope at small angles, for example and as shown in Fig. 8), and to other viscous effects such as the manifestation of transitional separation bubbles. The presence of a separation bubble induces additional pressure fluctuations around the point of bubble formation (with respect to its inviscid counterpart), as previously shown in Fig. 10.

The particular case of 9.5 m\({\cdot }\mathrm{{s}}^{-1}\) clear depicts the transition from stable LCOs to unstable response (the test was manually interrupted to avoid eventual damages to the structure and other nonlinear behaviors related to large deformation of the springs, which are not included in the scope of this study). For airflow speeds within the critical range the response is stable and repeatable. As typical of nonlinear aeroelastic systems, the response settles onto a LCO with amplitude accordingly to the airflow speed and irrespective of the applied initial condition.

Unfiltered raw data are shown in the graphs of Fig. 12. The calculation of the pitch and plunge structural velocities, aerodynamic angle of attack, and dimensionless pitch rate, from the unfiltered data yields slightly noisy results. Since the calculated quantities are useful inputs for a number of aerodynamic models such as the Beddoes-Leishman model, for example, less noisy data is probably preferred. The Savitzky-Golay polynomial smoothing filter was therefore applied (with an order of 4 and frame length of 49), as depicted in Fig. 13 for an arbitrary case of Fig. 12. It is out of the scope to present a filter comparison, but we consider the results superior to that obtained by other typical filters tested (this could be different in other cases). With clearer aerodynamic data, a numerical aerodynamic model (e.g., Beddoes-Leishman theory) could be used to estimate the unsteady aerodynamic loading acting on the airfoil.

Fig. 13
figure 13

Pitch and plunge (structural) velocities calculated from unfiltered raw data and from filtered data with Savitzky-Golay filtering technique (a). Corresponding calculated (aerodynamic) angle of attack and pitch rate (b) (input quantities required by the Beddoes-Leishman aerodynamic model, for example)

Full size image

4.2 Frequency and bifurcation characteristics with increasing airflow speed

The effect of increasing airflow speed on the frequency and amplitudes of oscillation is discussed next for the range of airflow speeds with stable aeroelastic response. Figure 14 displays phase portraits for the pitch and plunge degrees of freedom. The applied initial conditions are indicated by markers (in the plunge graph) in the color corresponding to the airflow speed (annotated in the pitch graph). The initial conditions are arbitrary to show the evolution of the aeroelastic displacements towards the steady-state response (either smaller or larger than the stable orbits). Stable orbits are observed from 8.1 m\({\cdot }\mathrm{{s}}^{-1}\) up to 9.5 m\({\cdot }\mathrm{{s}}^{-1}\), when the response changes to unstable regardless of any negligibly small initial condition. As the pitch angle achieves a magnitude of about 20\(^\circ\) a significant dissymmetry manifests in the elastic restoring moment (for structural reasons due to the torsional stiffness design with the wire spring) and the test is interrupted to preserve the experimental apparatus.

Fig. 14
figure 14

Pitch (a) and plunge (b) phase portraits at different airflow speeds between the cut-in and the cut-out speeds. Markers in (b) indicate the initial condition for the orbit represented in the same color (applied in the form of a nonzero initial displacement with zero velocity in the plunge DoF). Arrows indicate the evolution of the state variables, and the orbit in dashed line is unstable

Full size image

Figure 15 displays bifurcation diagrams for the measured aeroelastic displacements and calculated aerodynamic quantities. Peak and root-mean square (RMS) amplitudes are shown for convenience. While the structural motion (\(\theta\), \({\dot{\theta }}\), h, \({\dot{h}}\)) is required for the calculation of the aerodynamic input (\(\alpha\), q) when numerically solving, for example, the Beddoes-Leishman dynamic stall model, it is also important to observe the displacements during the experimental tests for the structural safety of the apparatus. This is a point of concern since we are interested in nonlinear post-flutter oscillations with manifestation of the dynamic stall phenomenon at large angles of attack, but that will take place at even larger structural pitch angles. For this reason, future studies should consider an improved torsional stiffness mechanism able to achieve substantially large pitch angles while maintaining linearly elastic behavior (unless structural nonlinearities are intentionally of concern, as usual in energy harvesting cases).

Fig. 15
figure 15

Pitch and plunge structural motion bifurcation diagrams (a). Aerodynamic angle of attack and pitch rate (b). Peak amplitude values and root mean square values are shown

Full size image

Figure 16 displays the amplitude spectra of the pitch and plunge displacements, aerodynamic angle of attack and pitch rate, in the range of airflow speeds with self-sustained oscillations. The graphs show the single-sided re-scaled discrete Fourier transform of the time-domain data. The dominant frequency of oscillation slightly increases with increasing airflow speed, as also shown in Fig. 17. The proximity of the oscillation frequency to the natural frequency of the plunge DoF indicates the plunge DoF is the unstable one. It could be possibly different for other model parameters, and in such a case the oscillation frequency could pursue the pitch DoF natural frequency (changes in the amplitudes of oscillations would be likely to occur as well). The uncoupled natural frequencies of the pitch and plunge DoFs are indicated by markers in the graph, with contour markers for undamped frequencies and solid markers for damped frequencies. The actual, coupled frequencies are expected to be slightly smaller than the uncoupled values, specially for the pitch DoF since the plunge DoF is dominant. The stable LCO frequency, however, is more relevant and is highlighted in the right-hand side graph.

Fig. 16
figure 16

Structural pitch and plunge amplitude spectra (a). Aerodynamic angle of attack and pitch rate amplitude spectra (b). Increasing oscillation frequencies correspond to increasing airflow speeds in the range of stable LCOs

Full size image
Fig. 17
figure 17

Oscillation frequency versus airflow speed. The pitch and plunge coupled frequencies coalesce as the airflow speed increases (a). Detail of the experimental frequency increase with increasing airflow speed for the region of stable LCOs (b). Markers in (a) indicate the pitch and plunge natural frequencies (contour and solid markers for undamped and damped frequencies, respectively)

Full size image

4.3 Final remarks

The main goal of this study is the construction and evaluation of a classical PAPA model in wind tunnel bench tests. While the focus is on the experimental verification of flutter-related behavior, the identification of aeroelastic parameters and data acquisition during nonlinear post-flutter airfoil motion is useful for eventual other studies focused on the numerical simulation of the airfoil aeroelastic behavior. It is mentioned in the text that unsteady aerodynamic models, such as the Beddoes-Leishman [13] and Brown-Dowell [20] models (among others), could be employed to simulate the airfoil response in both linear and nonlinear cases, where the nonlinear case may be either structural, aerodynamic, or a combination of both.

The possibility of investigating aeroelastic problems with combined nonlinear effects of different natures (structural and aerodynamic) is a significant advantage of the Beddoes-Leishman model over linear models, since pertinent phenomena such as the dynamic stall can be addressed. This work, therefore, is an effort to contribute with more experimental data of flutter and post-flutter airfoil wind tunnel bench tests to the literature of Aeroelasticity. In this sense, the experimental data can be freely obtained upon request from the corresponding author.

5 Conclusion

A traditional pitch-and-plunge-airfoil (PAPA) model is considered in this study to experimentally investigate the aeroelastic behavior of an airfoil undergoing nonlinear post-flutter oscillations during wind tunnel bench tests. An airfoil prototype was designed, built, characterized, and tested for a range of airflow speeds. Damped airfoil response was observed at airflow speeds below 8.0 m\({\cdot }\mathrm{{s}}^{-1}\) irrespective of the magnitude of the applied initial condition. Stable limit-cycle oscillations (LCOs) were observed at airflow speeds between 8.1 m\({\cdot }\mathrm{{s}}^{-1}\) and about 9.5 m\({\cdot }\mathrm{{s}}^{-1}\), with amplitudes increasing for increasing airflow speed. Unstable oscillations were observed at airflow speeds equal to 9.5 m\({\cdot }\mathrm{{s}}^{-1}\) and above for any small initial condition applied.

The steady-state oscillations within the stable range are certainly aerodynamically nonlinear since the angle of attack peak amplitudes are relatively large and significantly exceed the critical stall angle of attack as the airfoil oscillates (for the considered flow conditions, i.e., Reynolds number range between 1\(\times\)10\(^{5}\) and 2\(\times\)10\(^{5}\)). It is also possible that the nonlinear behavior posses some structural contribution due to large deformation of the springs that confer stiffness to the pitch and plunge degrees of freedom, but this possibility was previously investigated and found not relevant in this work (the tests were interrupted when the displacements achieved magnitudes considered too large for our experimental apparatus). Therefore, it is believed that the majority of the observed nonlinear behavior is of aerodynamic nature and associated with the dynamic stall phenomenon. This work contributes with the field of Aeroelasticity by providing additional experimental data of nonlinear airfoil wind tunnel bench tests that may be useful in future numerical modeling and simulation works.