1 Introduction

In mechanical engineering and dynamic system, mechanical transmission part is essential and necessary, and it is one of the most important technologies in the manufacturing industry. The transmission elements are the specific implement parts and its characteristics directly determine the accuracy, efficiency and other functions of the whole mechanical system [1]. Transmission elements occupy a vital place in the field of aerospace, power engine and so on. The worm and worm gear as the typical transmission element, which are widely applied to mechanical equipment in mining, transportation and other industries to transfer motion and power between two staggered shafts by spatial meshing form [2]. The main characteristics of worm drive are transmission stability, large bearing capacity, compact structure and self-locking, thus, it is often used in gearbox systems and reduction mechanisms to achieve the large reduction ratio. However, the friction loss and manufacturing cost of worm drive is relatively large, wear and heat may also occur due to the material fatigue and aging. Therefore, for improving the transmission performance of worm drive, it is necessary to develop feasible methods so as to reduce friction loss and enhance meshing efficiency in mechanical manufacturing.

Among many forms of the existing worm pair, the planar double-enveloping hourglass worm drives were initially invented and reported in 1765 [3, 4]. It is particularly suitable for heavy load and high-speed application scenarios of modern machinery. Existing studies have proposed numerous feasible and effective methods for researching and analyzing the performance of planar double-enveloping worm drive theoretically and experimentally [5]. Polowniak et al. [6] introduced a mathematical model of a double-enveloping worm gear for determining the tooth surface on worm gear, the tooth surface formation formed during whole processing by external edge of tool was presented. Mohan and Shunmugam [7] analyzed the contact property in double enveloping worm drive with tooth geometrical simulation in representing hob tooth by worm axial sections. The results indicated that it is possible to generate worm gear profile by machining a mating gear with a single fly tool, and intermittent contact exist at worm end sections. Zhao et al. [8] established a meshing theory for dual tori double-enveloping toroidal worm, the influence of technological parameters on meshing characteristics and behavior were studied.

The transmission performance of traditional hourglass worm drive is susceptible to manufacturing and assembly errors, the accuracy requirements and the cost of tools used for machining worm are also high. Moreover, the worm gear mechanism and the tooth contact analyzation have received increasing attention [9,10,11]. Therefore, to improve the transmission performance of worm pair, it is necessary to develop the worm pairs with novel transmission types in mechanical engineering. Chen et al. [12] investigated a new planar internal gear single-enveloping worm pair, and the corresponding experiment test for confirmation was carried out. Mu et al. [13] described the theoretical establishment with novel meshing principle for an involute worm drive using the frame of meshing principle on involute helicoid, the results showed that the conjugate area could almost cover the whole gear tooth surface.

In recent years, with the development of spatial meshing theory and differential geometry, there are many existing researchers have proposed plenty of worm pairs with pin roller, taper roller, ball or other components. The purpose is to replace the sliding friction between tooth surfaces with the rolling friction by rollers, so that the friction loss can be greatly reduced [14, 15]. Liu et al. [16] proposed a non-parallel double-roller enveloping hourglass worm drive based on the study of rolling cone enveloping hourglass worm pair, the relative coordinates, equations of contact line and spiral line on tooth surfaces were deduced. Ye [17] confirmed the influence of the position of contact-point and contact-line tendency on meshing velocity and nonzero principle relative normal curvature for the cylindrical worm pairs. Ren et al. [18] introduced a method of point-contact conjugated hourglass worm based on generated tooth surface theory, its conjugate surface formation mechanism was verified by numerical calculation.

In this study, a novel type of double-roller hourglass worm drive is established based on the planar double-enveloping hourglass worm pair, for achieving friction reduction and improving meshing efficiency. Wherein, the worm part adopts the worm in double-enveloping hourglass worm pair and the worm tooth surface is formed by the tool gear envelope, which is the first enveloping; the second enveloping is the process of the worm envelopes the original gear tooth surface, here, it is replaced by two rows of cylinder rollers, and the common tangent plane of two rollers is replaced the original enveloping surface and contact with worm in meshing. We focus on changing the transmission form of the traditional worm pair, and combined the advantages of end-face drive worm pair and single-roller cylinder hourglass worm pair. That is, the sliding friction between the tooth surfaces can be replaced with rolling friction by adopting two rows of rollers, and the line-contact is transformed into point-contact so that transmission performance can be largely improved. In theoretical model, the meshing theory system of double-roller hourglass worm pair was modeled and analyzed derived from meshing principle, the meshing equation, tooth surface equation and contact-line equation were deduced. Next, the solid model of double-roller hourglass worm and worm gear parts were modeled separately and assembled together, the equations of relative motion velocity and meshing efficiency at contact point was derived. We focus on the effects of the parameters of cylinder roller radius, enveloping surface angle and friction coefficient on transmission performance of relative motion velocity and meshing efficiency in the double-roller hourglass worm pair.

2 Meshing system of the worm drive

In the meshing system of the double-roller hourglass worm pair, the worm part adopted from the worm in the traditional planar double enveloping hourglass worm drive. The worm tooth surface was formed by a single enveloping movement with the tooth surface of tool gear as the original surface by a certain transmission ratio; and the worm gear part was modeled based on the above enveloping, composed of two slices of gears and several rollers. Figure 1 shows the schematic diagram of the double-roller hourglass worm drive. As the traditional worm gear tooth surface was replaced by roller, which transformed the sliding friction between the original tooth surfaces into rolling friction, for reducing the friction loss and improving meshing efficiency [19].

Fig. 1
figure 1

Schematic diagram of double-roller hourglass worm drive

Full size image

2.1 Coordinate systems

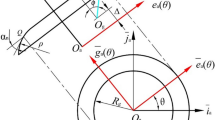
The enveloping relationship of the worm drive is shown in Fig. 2 [20]. The static coordinate system \({\sigma }_{0}^{\mathrm{^{\prime}}}\left({O}_{0}^{\mathrm{^{\prime}}}:{i}_{0}^{\mathrm{^{\prime}}},{j}_{0}^{\mathrm{^{\prime}}},{k}_{0}^{\mathrm{^{\prime}}}\right)\) and \({\sigma }_{1}^{\mathrm{^{\prime}}}\left({O}_{1}^{\mathrm{^{\prime}}}:{i}_{1}^{\mathrm{^{\prime}}},{j}_{1}^{\mathrm{^{\prime}}},{k}_{1}^{\mathrm{^{\prime}}}\right)\) express the original position of tool gear and worm, respectively. The coordinate systems for \({\sigma }_{0}\left({O}_{0}:{i}_{0},{j}_{0},{k}_{0}\right)\), \({\sigma }_{1}\left({O}_{1}:{i}_{1},{j}_{1},{k}_{1}\right)\) and \({\sigma }_{s}\left({O}_{s}:{i}_{s},{j}_{s},{k}_{s}\right)\) are fixation connected with tool gear, worm, and tooth surface \({\Sigma }_{0}\) of tool gear, respectively. \({\omega }_{0}\) and \({\omega }_{1}\) are the angular velocity vectors for tool gear and worm, the corresponding rotation angles are \({\varphi }_{0}\) and \({\varphi }_{1}\), and the ratio of transmission can be defined as \({i}_{01}={\varphi }_{0}/{\varphi }_{1}\), \(\left(={Z}_{1}/{Z}_{0}\right)\). \(a\) is the central distance of the double-roller hourglass worm drive, \(\beta\) is enveloping surface angle, and the rotation directions correspond to the right-hand worm coordinate system.

Fig. 2
figure 2

The coordinates for worm with tool gear in first enveloping and for worm and worm gear in second enveloping

Full size image

2.2 Equations of coordinate transformation and worm tooth surface

Based on Fig. 2, the transformation matrixes between various coordinates are as follows [20, 21]:

The transformation matrix \({M}_{1{1}^{\mathrm{^{\prime}}}}\) from \({\sigma }_{1}\) to \({\sigma }_{1}^{\mathrm{^{\prime}}}\).

$${M}_{1{1}^{\mathrm{^{\prime}}}}=\left[\begin{array}{lll}\mathrm{cos}{\varphi }_{1}& \mathrm{sin}{\varphi }_{1}& 0\\ -\mathrm{sin}{\varphi }_{1}& \mathrm{cos}{\varphi }_{1}& 0\\ 0& 0& 1\end{array}\right].$$
(1)

The transformation matrix \({M}_{{0}^{\mathrm{^{\prime}}}0}\) from \({\sigma }_{0}^{\mathrm{^{\prime}}}\) to \({\sigma }_{0}\).

$${M}_{{0}^{\mathrm{^{\prime}}}0}=\left[\begin{array}{lll}\mathrm{cos}{\varphi }_{0}& \mathrm{sin}{\varphi }_{0}& 0\\ -\mathrm{sin}{\varphi }_{0}& \mathrm{cos}{\varphi }_{0}& 0\\ 0& 0& 1\end{array}\right].$$
(2)

The transformation matrix \({M}_{{1}^{\mathrm{^{\prime}}}{0}^{\mathrm{^{\prime}}}}\) from \({\sigma }_{{1}^{\mathrm{^{\prime}}}}\) to \({\sigma }_{0}^{\mathrm{^{\prime}}}\).

$${M}_{{1}^{\mathrm{^{\prime}}}{0}^{\mathrm{^{\prime}}}}=\left[\begin{array}{lll}1& 0& 0\\ 0& 0& -1\\ 0& 1& 0\end{array}\right].$$
(3)

The transformation matrix \({M}_{0s}\) from \({\sigma }_{0}\) to \({\sigma }_{\mathrm{s}}\).

$${M}_{0s}=\left[\begin{array}{lll}1& 0& 0\\ 0& \mathrm{cos}\beta & \mathrm{sin}\beta \\ 0& -\mathrm{sin}\beta & \mathrm{cos}\beta \end{array}\right].$$
(4)

The transformation matrix \({M}_{10}\) from \({\sigma }_{1}\) to \({\sigma }_{0}\) was derived.

$${M}_{10}={M}_{1{1}^{\mathrm{^{\prime}}}}{M}_{{1}^{\mathrm{^{\prime}}}{0}^{\mathrm{^{\prime}}}}{M}_{{0}^{\mathrm{^{\prime}}}0}=\left[\begin{array}{lll}\mathrm{cos}{\varphi }_{0}\mathrm{cos}{\varphi }_{1}& -\mathrm{sin}{\varphi }_{0}\mathrm{cos}{\varphi }_{1}& -\mathrm{sin}{\varphi }_{1}\\ -\mathrm{cos}{\varphi }_{0}\mathrm{sin}{\varphi }_{1}& \mathrm{sin}{\varphi }_{0}\mathrm{sin}{\varphi }_{1}& -\mathrm{cos}{\varphi }_{1}\\ \mathrm{sin}{\varphi }_{0}& \mathrm{cos}{\varphi }_{0}& 0\end{array}\right].$$
(5)

The radial vector \({r}_{0}^{(1)}\) for origin coordinate \({O}_{0}\) expressed in \({\sigma }_{1}\), \({r}_{01}^{(0)}\) for origin coordinate \({O}_{1}\) in \({\sigma }_{0}\), \({r}_{0s}^{(0)}\) for origin coordinate \({O}_{s}\) in \({\sigma }_{0}\) were derived based on above transformation matrixes [2, 3], as shown below.

$$\left.\begin{array}{l}{r}_{0}^{(1)}={\left[\begin{array}{ccc}a\mathrm{cos}{\varphi }_{1}& -a\mathrm{sin}{\varphi }_{1}& 0\end{array}\right]}^{T}\\ {r}_{01}^{(0)}={\left[\begin{array}{lll}-a\mathrm{cos}{\varphi }_{0}& -a\mathrm{sin}{\varphi }_{0}& 0\end{array}\right]}^{T}\\ {r}_{0s}^{(1)}={\left[\begin{array}{ccc}0& -{r}_{b}& 0\end{array}\right]}^{T}\end{array}\right\}.$$
(6)

Based on the gear meshing principle, the relative velocity of meshing point in coordinate \({\sigma }_{0}\) and \({\sigma }_{1}\) has to satisfy the meshing function (Eq. (7)), \({V}^{\left(01\right)}\) is the relative velocity vector of the worm with respect to gear on the meshing point, and \({\varvec{n}}\) is unit normal vector.

$${V}^{\left(01\right)}\cdot {\varvec{n}}=0.$$
(7)

The meshing equation \(\phi\) was expressed in \({\sigma }_{0}\), as shown in Eq. (8). Wherein, \({r}_{b}\) is the worm gear base radius, \(u\) and \(v\) are the tooth profile parameters.

$$\phi ={a}_{1}u+{b}_{1}v+{c}_{1},$$
(8)
$$\left.\begin{array}{l}{a}_{1}=sin\beta cos{\varphi }_{0}-{i}_{01}cos\beta \\ {b}_{1}=-sin{\varphi }_{0}\\ {c}_{1}=\left({r}_{b}\mathrm{sin}{\varphi }_{0}+{a}_{0}\right)sin\beta \end{array}\right\}.$$
(9)

The original contact lines between tool tooth surface \({\Sigma }_{0}\) and worm surface \({\Sigma }_{1}\) accord with meshing equation, it is derived by uniting these two equations in \({\sigma }_{0}\) as shown below.

$$u\left(\mathrm{sin}\beta \mathrm{cos}{\varphi }_{0}-{i}_{01}\mathrm{cos}\beta \right)-v\mathrm{sin}{\varphi }_{0}+\left({r}_{b}\mathrm{sin}{\varphi }_{0}+a\right)\mathrm{sin}\beta =0,$$
(10)
$$\left.\begin{array}{l}{x}_{0}=u\\ {y}_{0}=vsin\beta -{r}_{b}\\ {z}_{0}=vcos\beta \end{array}\right\}.$$
(11)

The worm tooth surface \({\Sigma }_{1}\) is the aggregation of contact lines in \({\sigma }_{0}\). It can be obtained by transforming the contact line equation on tooth surface \({\Sigma }_{0}\) of tool gear from \({\sigma }_{0}\) to \({\sigma }_{1}\) as follows:

$$u\left(\mathrm{sin}\beta \mathrm{cos}{\varphi }_{0}-{i}_{01}\mathrm{cos}\beta \right)-v\mathrm{sin}{\varphi }_{0}+\left({r}_{b}\mathrm{sin}{\varphi }_{0}+a\right)\mathrm{sin}\beta =0,$$
(12)
$$\left.\begin{array}{l}{x}_{1}=\left({x}_{0}\mathrm{cos}{\varphi }_{0}-{y}_{0}\mathrm{sin}{\varphi }_{0}+{a}_{0}\right)cos{\varphi }_{1}-{z}_{0}sin{\varphi }_{1}\\ {y}_{1}=\left({x}_{0}\mathrm{cos}{\varphi }_{0}-{y}_{0}\mathrm{sin}{\varphi }_{0}+{a}_{0}\right)sin{\varphi }_{1}-{z}_{0}cos{\varphi }_{1}\\ {z}_{1}={x}_{0}sin{\varphi }_{0}+{y}_{0}cos{\varphi }_{0}\end{array}\right\}.$$
(13)

The above equations are applied to calculate and form the right side of slot on worm profile, and the corresponding left side can be generated by same iteration method.

2.3 Position determination of upper and lower rollers

The schematic diagram of meshing position of a certain cylinder roller in this worm drive is expressed in Fig. 3. The left part of Fig. 3 presents the profile angle and rollers plane geometry diagram. In order to realize the maximum extent meshing in this double-roller hourglass worm system, the positions of cylinder rollers on tooth surface of worm gear are important. Analyzing from the view of contact lines, it means that the roller surfaces should be intersected with the contact lines on the tooth surface of original worm gear as much as possible.

Fig. 3
figure 3

Schematic diagram of tooth profile shape angle and position for upper and lower rollers

Full size image

As shown in the right part of Fig. 3, \({E}_{r}\) is the offset distance between the center of rollers and the worm gear. The profile angle \(\alpha\), upper roller offset distance \({E}_{ru}\) and lower roller offset distance \({E}_{rl}\) are derived by geometric relation with figure based on sine theorem [16], as shown below.

$$\alpha =\mathrm{arcsin}\left(\frac{{r}_{r}{r}_{1}}{\mathrm{cos}\beta }\right),$$
(14)
$$\left.\begin{array}{l}{E}_{ru}={v}_{1}cos\beta \\ {E}_{rl}={E}_{r}-\left({r}_{b}-{E}_{r}\mathrm{tan}\beta \right)sin\beta \end{array}\right\},$$
(15)
$$\left.\begin{array}{l}{v}_{1}=\frac{2{E}_{r}}{\mathrm{cos}\beta }-\frac{{r}_{r}}{\mathrm{tan}\beta }+\frac{{r}_{r}-{E}_{r}\mathrm{tan}\beta }{\mathrm{sin}\beta }\\ {v}_{2}=\frac{{r}_{r}}{\mathrm{tan}\beta }-\frac{{r}_{b}-{E}_{r}\mathrm{tan}\beta }{\mathrm{sin}\beta }\end{array}\right\}.$$
(16)

The contact points between worm tooth surface and the surface of upper and lower rollers are presented in Fig. 4. The upper and lower rollers are in contact with the left and right tooth surfaces of the worm for realizing the non- backlash meshing between the worm and gear during transmission process. In figures, the black solid lines represent the contact lines between the worm and the original gear from the planar double-enveloping hourglass worm pair, they can be obtained by Eq. (10); the black dashed lines are the gear midplane of two rollers, which is corresponded to the right part of Fig. 3; the upper and lower roller offset distance \({E}_{ru}\) and \({E}_{rl}\) were obtained by Eq. (15), which were marked in red; the blue points are the contact points when the roller meshes with worm tooth surface.

Fig. 4
figure 4

Contact points of upper roller and lower roller on worm tooth surface (\(a=320\) mm, \({Z}_{0}=1\), \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \({r}_{r}=10\) mm, \(\beta =6.4^\circ\))

Full size image

3 Solid model of the double-roller hourglass worm pair

3.1 Modeling of worm tooth profile

According to the structure characteristics of the worm, there is one special symmetrical point on the tooth surface, which makes the worm tooth profile symmetrical on the axial section where this point located. In other words, a unique point existed on reference circle of one side tooth surface of the worm, and the space between this point to axial section is equal to the half of chord length corresponding to the tooth thickness in reference circle. The calculation of this special point is based on Eq. (17) as the objective function, and the corresponding coordinate value \(\left({x}_{1},{y}_{1},{z}_{1}\right)\) on the tooth surface in \({\sigma }_{1}\) can be obtained by the optimization iteration method. Wherein, \({\psi }_{s}\) is the teeth thickness ratio and \({s}_{0}\) is the thickness on reference circle of tool gear. And the axial section angle \({\varphi }_{p}\) corresponding to the symmetrical point was obtained by Eq. (18) combined with the worm tooth surface equation (Eq. (12)). The representative input parameters in this double-roller hourglass worm model are as follows: \(a=320\) mm, \({Z}_{0}=1\), \({Z}_{1}=63\), \({i}_{01}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \({c}^{\mathrm{^{\prime}}}=0.2\), \({K}^{\mathrm{^{\prime}}}=0.3\), \({h}_{a}^{\mathrm{^{\prime}}}=0.7\), \({r}_{r}=10\) mm, \(\beta =6.4^\circ\), \({\psi }_{s}=0.5\). And other calculation parameters of this model can be obtained by the basic equations based on gear meshing theory.

$$\left.\begin{array}{l}{z}_{1}+{\psi }_{s}{s}_{0}=0\\ {\left(a-\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}\right)}^{2}+{z}_{1}^{2}-{r}_{1}^{2}=0\end{array}\right\},$$
(17)
$${\varphi }_{p}=\mathrm{arctan}\left({y}_{1}/{x}_{1}\right).$$
(18)

The initial central position of worm modeling was determined as the value of axial section angle \({\varphi }_{p}\), the interval angle was selected as \(\Delta \varphi =20^\circ\), which expanded to upper- and lower-half respectively for forming the whole worm tooth profile. The range of worm rotational angle \({\varphi }_{1}\) is decided by the enveloping tooth number \({Z}^{\mathrm{^{\prime}}}\). Generally, the number of teeth enveloping by worm gear is about \(10\mathrm{\%}\) of its total number, and it was selected as \({Z}^{\mathrm{^{\prime}}}=6\) in this model, thus, the value range of worm rotational angle \({\varphi }_{1}\) is \(\left[-6\uppi , 6\uppi \right]\). The modeling of worm tooth profile consists of two nested loops: taking the worm tooth surface equation (Eq. (12)) as iteration function; the gear rotation angle \({\varphi }_{0}\) was selected as the outer loop parameter, and its value range is \(\left[-6\uppi /{i}_{01}, 6\uppi /{i}_{01}\right]\); inner loop parameter was taken as the profile parameter \(u\), which represented the distance between the grid node and the dedendum on worm profile under a certain value of \({\varphi }_{0}\). It was iterated and calculated by Eq. (19) as the objective function. Where, \({r}_{a0}\) and \({r}_{f0}\) is the topping flank radius of worm gear and worm, respectively.

$$\left.\begin{array}{l}{\left(a-\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}\right)}^{2}+{z}_{1}^{2}-{r}_{f0}^{2}=0\\ {\left(a-\sqrt{{x}_{1}^{2}+{y}_{1}^{2}}\right)}^{2}+{z}_{1}^{2}-{r}_{a0}^{2}=0\end{array}\right\}.$$
(19)

The above two objective functions in Eq. (19) calculated the parameters of \({u}_{f}\) and \({u}_{a}\) corresponding to the dedendum and addendum point of the worm, respectively. The upper-half of left tooth profile of worm was drawn and presented as shown in the left part of Fig. 5, and the symmetrical point is marked in red. And then, rotating the position of symmetrical point on left tooth profile to the axial section where the symmetrical axis is located. According to the symmetrical characteristics of worm tooth profile, the right-side tooth profile can be obtained by rotating \(180^\circ\) of grid matrix of left-side tooth profile along symmetrical axis (y-axis). In this way, the both two tooth profiles of worm were generated and shown in the right part of Fig. 5.

Fig. 5
figure 5

The upper-half part in left tooth profile of worm and left- and right-side tooth profiles of worm

Full size image

As the symmetrical relations between the left- and right-side tooth profiles of worm, the addendum and dedendum of both tooth profiles were connected and combined through its parameter matrix, for generating the worm addendum and dedendum surfaces. The initial digitization model of worm was established and analyzed by MATLAB, as its powerful capabilities in numerical iteration and plotting for generating the complex surfaces according to the given equations. In addition, Pro/E is a popular 3D modeling software, which was widely used for parametric design of mechanical parts, however, it is limited in generating curves and surfaces directly from complex equations. And the worm tooth profile studied in this research is relatively complex with restricting mathematical equations. Therefore, we adopted the effective combination of two software, the grid nodes on the worm tooth surfaces were calculated by MATLAB firstly, and then, the processed data and matrixes were imported into Pro/E to generate and obtain the final solid model of worm profile. The combination of two software can effectively and intuitively construct the complex tooth profile of worm surfaces, and the digitization and the solid model of worm tooth profile are shown in Fig. 6.

Fig. 6
figure 6

The digitization tooth profile of worm tooth surface and the corresponding solid model

Full size image

3.2 Modeling of worm gear and assemble

Comparing with the solid model of worm, the modeling process of worm gear is relatively simple due to the shape of each inside consisted component is regular, and the specific modeling steps were as follows: the position of upper and lower rollers can be determined by Eqs. (15) and (16), the parts of cylinder roller, the left and right half-piece gear was established respectively in Pro/E with referring to gear design literature; next, the two half-piece gear were assembled together into integration by bolting; then, the upper and lower rollers were installed on the two half-pieces of gear by using support shafts respectively; finally, the two rollers were circumference arrayed along the gear central axis with the offset angle selected as \({\theta }_{t}=5.71^\circ\). At this moment, the solid model of worm gear in double-roller hourglass worm pair was completed as expressed in the left part of Fig. 7.

Fig. 7
figure 7

The solid model of worm gear and assembled with worm

Full size image

After completing the solid model of the worm tooth profile in Sect. 3.1, it is necessary to add the inside shaft and be chamfered. In addition, because the incomplete meshing tooth existed at the two ends of worm, which need to be removed for revision. That is, plotting a tangent curve at both ends from addendum to dedendum of the worm, stretching along the worm axis for removing them. Importing the gear solid model for completing assemble as shown in right part of Fig. 7. Finally, the global interference and clearance check was proceeded to the double-roller hourglass worm pair to ensure the continuity and feasibility during the meshing transmission.

Compared with the single-roller hourglass worm pair, the superior characteristics for the proposed double-roller worm pair is as follows: due to the two rows of rollers are uniform distributed on worm gear, during the meshing process, the upper and lower rollers meshed with the left and right tooth surfaces of worm, respectively. The non-backlash meshing between the worm and worm gear can be realized, which could reduce the noise and vibration in transmission, and improving the operation stability.

4 Analysis of the relative motion velocity between meshing tooth surfaces

4.1 Movable coordinates and equations of relative velocity

As shown in Fig. 2, the transform relation of radial vector between \({\sigma }_{1}\) and \({\sigma }_{0}\) is given.

$$r={M}_{10}{r}_{0}+{r}_{0}^{\left(1\right)}.$$
(20)

\({M}_{10}\) is the transform matrix for \({\sigma }_{1}\) and \({\sigma }_{0}\), which is identity matrix. \({r}_{0}^{\left(1\right)}\) is coordinate origin of \({\sigma }_{0}\) expressed in \({\sigma }_{1}\), and \({r}_{0}^{\left(1\right)}={\left[\mathrm{0,0},-{E}_{r}\right]}^{T}\). The relative velocity is derived in Eq. (21).

$${V}^{\left(01\right)}={\omega }^{(01)}\times {r}_{0}-{\omega }^{(1)}\times \varepsilon ,$$
(21)

wherein, \({\omega }^{(01)}={\omega }^{(0)}-{\omega }^{(1)}\), the parameters of \({\omega }^{(0)}\), \({\omega }^{(1)}\), and \(\varepsilon\) is expressed in \({\sigma }_{0}\) as follows:

$$\left.\begin{array}{l}{\omega }^{(0)}={i}_{01}{k}_{0}\\ {\omega }^{(1)}={i}_{0}sin{\varphi }_{0}+{j}_{0}cos{\varphi }_{0}\\ \varepsilon =a\left({i}_{0}\mathrm{cos}{\varphi }_{0}-{j}_{0}\mathrm{sin}{\varphi }_{0}\right)\end{array}\right\}.$$
(22)

Therefore, the relation velocity can be obtained.

$$\left.\begin{array}{l}{V}_{x}^{\left(01\right)}=-v\mathrm{cos}\beta \mathrm{cos}{\varphi }_{0}-{i}_{01}\left(v\mathrm{sin}\beta -{r}_{b}\right)\\ {V}_{y}^{\left(01\right)}={i}_{01}u+v\mathrm{cos}\beta \mathrm{sin}{\varphi }_{0}\\ {V}_{z0}^{\left(01\right)}=-v\mathrm{sin}\beta \mathit{sin}{\varphi }_{0}-u\mathrm{cos}{\varphi }_{0}+a\end{array}\right\}.$$
(23)

The above equation is expressed in \({\sigma }_{1}\) as follows:

$$\left.\begin{array}{l}{V}_{x}^{\left({1}^{\prime}1\right)}=-v\mathrm{cos}\beta \mathrm{cos}{\varphi }_{0}-{i}_{01}\left(v\mathrm{sin}\beta -{r}_{b}\right)\\ {V}_{y}^{\left({1}^{\prime}1\right)}={i}_{01}u+v\mathrm{cos}\beta \mathrm{sin}{\varphi }_{0}\\ {V}_{z0}^{\left({1}^{\prime}1\right)}=-(v\mathrm{sin}\beta -{r}_{b})\mathrm{sin}{\varphi }_{0}+u\mathrm{cos}{\varphi }_{0}+a\end{array}\right\}.$$
(24)

Figure 8 presents the coordinate \({\sigma }_{g}\left({O}_{g}:{i}_{g},{j}_{g},{k}_{g}\right)\) with the cylinder roller as an object. The coordinate value of a meshing point \(P\) on roller surface is expressed as \(\left({x}_{g},{y}_{g},{z}_{g}\right)\). The vector \({e}_{\tau }\), \({e}_{a}\) and \({n}_{r}\) is the unit vector along tangential, radial and normal direction, respectively, they are expressed in \({\sigma }_{1}\) as below.

$$\left.\begin{array}{l}{e}_{\tau }^{(1)}={M}_{1g}{e}_{\tau }^{(g)}+{r}_{g}^{\left(1\right)}\\ {e}_{a}^{(1)}={M}_{1g}{e}_{a}^{(g)}+{r}_{g}^{\left(1\right)}\\ {n}_{r}^{(1)}={M}_{1g}{n}_{r}+{r}_{g}^{\left(1\right)}\end{array}\right\},$$
(25)

wherein, \({M}_{1g}\) is the transform matrix of \({\sigma }_{1}\) and \({\sigma }_{g}\), \({r}_{g}^{\left(1\right)}\) is the vector column matrix of origin \({O}_{g}\) in \({\sigma }_{1}\), and \({r}_{g}^{\left(1\right)}={\left[{r}_{a1},\mathrm{0,0}\right]}^{T}\). Thus, the vector \({e}_{\tau }\), \({e}_{a}\) and \({n}_{r}\) is expressed in \({\sigma }_{0}\) (identity with \({\sigma }_{1}\)) as follows:

Fig. 8
figure 8

The movable coordinate system of cylinder roller

Full size image
$$\left.\begin{array}{l}{e}_{\tau }^{(0)}={j}_{0}sin\theta +{k}_{0}cos\theta \\ {e}_{a}^{(0)}={i}_{1}\\ {n}_{r}^{\left(0\right)}={j}_{0}cos\theta -{k}_{0}sin\theta \end{array}\right\}.$$
(26)

Therefore, the vector of roller surface and relative velocity at contact point are derived.

$${r}_{\mathrm{g}}=-\left({r}_{r}\mathrm{cos}\theta \right){i}_{g}+{r}_{r}\mathrm{cos}\theta {j}_{g}+u{k}_{g},$$
(27)
$$V={V}_{\tau }^{\left(10\right)}{e}_{\tau }^{(0)}+{V}_{a}^{\left(10\right)}{e}_{a}^{(0)}+{V}_{n}^{\left(10\right)}{n}_{r}^{(0)},$$
(28)
$$\left.\begin{array}{l}{V}_{\tau }^{\left(10\right)}=\left({i}_{01}u+v\mathrm{cos}\beta \mathrm{sin}{\varphi }_{0}\right)sin\theta +\left[-\left(v\mathrm{sin}\beta -{r}_{b}\right)\mathrm{sin}{\varphi }_{0}+u\mathrm{cos}{\varphi }_{0}+a\right]cos\theta \\ {V}_{a}^{\left(10\right)}=-vcos\beta cos{\varphi }_{0}-{i}_{01}\left(v\mathrm{sin}\beta -{r}_{b}\right)\\ {V}_{n}^{\left(10\right)}=\left({i}_{01}u+v\mathrm{cos}\beta \mathrm{sin}{\varphi }_{0}\right)cos\theta -\left[-\left(v\mathrm{sin}\beta -{r}_{b}\right)\mathrm{sin}{\varphi }_{0}+u\mathrm{cos}{\varphi }_{0}+a\right]sin\theta \end{array}\right\}.$$
(29)

4.2 The effect of enveloping surface angle

In this paper, the points in Figs. 9, 10, 11, 12, 13 represent the contact points between the meshing surfaces of rollers and worm, derived from theoretical calculation. The value of \(u\) was not plotted from 0, this is because when selected the special values of input parameters such as small roller radius or large enveloping surface angle, the contact points do not appear at the bottom part. And the contact lines overlap at bottom part on tooth surface, resulting in there are two different values of \(V\) corresponding to the same \(u\) in some cases as refer to Fig. 4.

Fig. 9
figure 9

Effect of enveloping angle on velocity (\(a=320\) mm, \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \({r}_{r}=10\) mm)

Full size image
Fig. 10
figure 10

Effect of cylinder roller radius on velocity (\(a=320\) mm, \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \(\beta =6.4^\circ\))

Full size image
Fig. 11
figure 11

Effect of enveloping angle on efficiency (\(a=320\) mm, \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \({r}_{r}=10\) mm, \(f=0.1\))

Full size image
Fig. 12
figure 12

Effect of roller radius on efficiency (\(a=320\) mm, \({Z}_{0}=1\), \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \(\beta =6.4^\circ\), \(f=0.1\))

Full size image
Fig. 13
figure 13

Effect of friction coefficient on efficiency (\(a=320\) mm, \({Z}_{1}=63\), \({b}_{0}=35\) mm, \({b}_{1}=75\) mm, \({r}_{r}=10\) mm, \(\beta =6.4^\circ\))

Full size image

The effect of enveloping surface angle on relative motion velocity of upper and lower roller is expressed in Fig. 9. The input rotational speed of worm and roller radius were set as \(n=1000\) \(\mathrm{r}/\mathrm{min}\). It depicts that for both upper and lower rollers, the enveloping surface angle has an influence on relative motion velocity at the contact point between meshing tooth surfaces. For upper roller, the relative velocity decreased with the increase of roller axial parameter \(u\), and the maximum velocity points located at the dedendum of roller. In addition, it decreased gradually with the decrease of \(\beta\). Moreover, at the position of roller dedendum, the value varies in \(\beta\) corresponded to a more obvious effect on relative velocity for both cases.

4.3 The effect of cylinder roller radius

The effect of cylinder roller radius on relative motion velocity is shown in Fig. 10, with enveloping surface angle \(\beta =6.4^\circ\). For upper roller, during the transmission process of gear and worm, the relative motion velocity at meshing point decreased with the increase value of \(u\) and \({r}_{r}\); however, the situation of enveloping angle and roller radius effect on the lower roller was opposites to upper roller in Figs. 9b and 10b. Furthermore, the too small roller radius may lead to incomplete contact between tooth surfaces of roller and worm, resulting in the situation for sparse contact, which is unbeneficial to transmission.

5 Analysis of the meshing efficiency

5.1 Equation of meshing efficiency

As shown in Fig. 8, the meshing point \(P\) on roller surface is suffered in the sliding friction force \({F}_{\tau }\) along the tangential direction, \({F}_{f}\) along the normal direction and the normal force \({F}_{n}\). Both \({F}_{\tau }\) and \({F}_{f}\) is in the tangent plane of meshing point \(P\). In this paper, the meshing efficiency for the double-roller hourglass worm pair is derived in Eq. (30), wherein, \({P}_{r}\) is the output power of the system, \({P}_{f}\) is meshing power loss, and \(f\) is friction coefficient.

$$\eta ={P}_{r}/\left({P}_{r}+{P}_{f}\right),$$
(30)
$$\left.\begin{array}{l}{P}_{r}=-{\omega }_{1}{r}_{1}cos\beta \left({r}_{a1}+u\right)\\ {P}_{f}=f{e}_{a}\sqrt{{\left({r}_{a1}+u\right)}^{2}+{r}_{r}^{2}}\end{array}\right\}.$$
(31)

5.2 The effect of enveloping surface angle

The effect of enveloping surface angle on meshing efficiency of upper and lower rollers is depicted in Fig. 11, and the roller radius and friction coefficient were set as \({r}_{r}=10\) mm and \(f=0.1\), respectively. It was clear that for both upper and lower rollers, the meshing efficiency fluctuated slightly in general. For upper roller, the meshing efficiency was highest at the initial meshing point of roller, and the different values in axial parameter \(u\) is the corresponded to different effect degree of \(\beta\) varies on \(\eta\), which is more obvious at dedendum. Besides, the meshing efficiency was increased with the \(\beta\) increase of each contact line for upper roller.

5.3 The effect of cylinder radius

The effect of roller radius on meshing efficiency of upper and lower roller is shown in Fig. 12, with \(\beta =6.4^\circ\) and \(f=0.1\). For upper roller, with the decrease of roller radius, the meshing efficiency increases slightly; the situation of enveloping angle and roller radius effect on lower roller is also shown the opposite to upper roller in Figs. 11b and 12b. It is worth noting that, in the case where the roller radius was too small to form the adequate contact in meshing surfaces although the efficiency increased. Therefore, in the process of \({r}_{r}\) selection, it should not only consider increasing meshing efficiency, but also take into account the density of contact lines on roller surface.

5.4 The effect of friction coefficient

The effect of friction coefficient on meshing efficiency for upper and lower rollers was expressed in Fig. 13, with the parameters of \({r}_{r}=10\) mm and \(\beta =6.4^\circ\). It can be seen that the friction coefficient has a large effect on meshing efficiency, and the meshing efficiency was significantly improved with the friction coefficient decreasing for both cases. Therefore, in the practical application, it is necessary to improve the lubrication conditions between the meshing tooth surfaces of worm and worm gear, select the appropriate lubrication methods, and keep the contact area in a good lubrication condition.

6 Conclusions

In this study, the specific theoretical analysis for transmission performance of a novel double-roller hourglass worm drive were proposed based on the meshing principle and differential geometry theory, the static and dynamic coordinate systems of worm and worm gear were established, respectively. The meshing equation, tooth surface equation and contact line equation of worm and gear were derived by the coordinating transformation. And the tooth surface of worm pair was constructed by the combination of MATLAB and Pro/E software for realizing 3D solid modeling of worm and gear and assembling. Moreover, the calculation equations of relative motion velocity and meshing efficiency of worm pair were derived. The theoretical variation laws of relative velocity and meshing efficiency at tooth surface contact point between worm and gear were analyzed and discussed in terms of enveloping surface angle, cylinder roller radius and friction coefficient, which were selected as the main parameters. The double-roller hourglass worm drive proposed in this study can be applied in the working condition of high-speed and light-load, and the present theoretical model will be confirmed and discussed by specific experiment in the near future. Based on the results, the conclusions of this study are as follows:

  1. (1)

    In the double-roller hourglass worm pair, the original gear tooth surface is replaced by cylinder rollers and the sliding friction at contact point can be transformed into rolling friction for realizing the purpose of reducing friction and improving meshing efficiency, which was verified by the theoretical model.

  2. (2)

    The effect of enveloping angle and roller radius on relative velocity and meshing efficiency was more obvious near location of worm gear dedendum for each case, but the effect is opposite between upper and lower rollers.

  3. (3)

    The meshing efficiency can be effectively improved by properly decreasing the friction coefficient.