1 Introduction

ECCs are a developing category of cementitious composites that are reinforced with high-performance fibers such as polyvinyl alcohol (PVA), polyethylene (PE), carbon, glass, steel, and natural fibers; however, the PVA and PE fibers are particularly popular due to their compatibility with the cementitious matrix; their ability to enhance the ductility of the composite significantly and display various micro-cracks features [1,2,3]. Li et al. [4] developed engineered cementitious composite (ECC) composites in the 1990s through the intentional modification of the matrix, fiber, and fiber-matrix interface, fiber volume fraction, orientation, slip-debonding mechanism, and stress transfer guided by the principles of micromechanics theory [5, 6]. The material has achieved a distinctive composition of high-performance fiber-reinforced cement composite (HP-FRCC), in which the overall volume fraction of fibers typically does not exceed 2% [5, 7, 8]. ECCs serve as a noteworthy illustration of a sustainable material that possesses the potential to enhance the economic aspects of construction projects while also addressing various technical challenges, e.g., cost, material consistency, workability, design codes, standards, and sustainability [22]. When subjected to tension, ECCs demonstrate a ductility that surpasses a strain value of 3% and exhibits acceptable flaws of less than 100 µm [8, 9]. Deng et al. [10] demonstrate lightweight ECC (LWECC) with an impressive high strain of > 12% and low density make ECC suitable for retrofitting structural parts, particularly in enhancing seismic performance [11] and lightweight structure application with low cost and low carbon footprint [12]. Moreover, it can potentially address the spalling in brittle concrete cover, which leads to the corrosion of embedded steel bars and subsequent premature deterioration of concrete structures [13].

The mechanical properties of ECCs (e.g., CS, TS, TSt) are mainly affected by the mix design, including the inclusion of cement matrix constituents and fiber variables [14, 15]. The composition of the mixture includes Portland cement (PC) along with environmentally beneficial supplementary cementitious materials (SCMs) such as class-F fly ash, class C fly ash, and ground granulated blast furnace slag (GGBS). These SCMs, together with micro-silica sand, chemical admixtures like superplasticizer and hydroxypropyl methylcellulose (HPMC), and water, not only enhance the performance of the concrete but also significantly contribute to the green and low-carbon development of civil engineering by reducing the carbon footprint associated with cement production. Predicting mechanical properties accurately through the integration of mixed parameters, like employing precise mixed proportions to attain the desired tensile strain capacity, in ECCs, could greatly improve the design process. This in turn could lead to a substantial decrease in experimental workload and cost. However, the material components of green ECCs are characterized by a high level of complexity and play a crucial role in reducing the carbon footprint. This poses challenges in accurately modeling the mechanical characteristics based on mixture design parameters through conventional regression studies [16], highlighting the need for innovative approaches to support the green and low-carbon development of civil engineering. There is a pressing need for the development of more robust and advanced modeling techniques to enhance the prediction capabilities of models.

Traditional approaches to discerning the relationships among various parameters typically rely on statistical analyses, which facilitate the construction of both linear and non-linear regression models [17, 18]. Nevertheless, these regression models are often constrained by their inherent limitations; they are bound to the relationships defined by the pre-established equations, whether linear or non-linear [19, 20]. To overcome these limitations, machine learning methodologies inspired by biological processes have been devised to effectively model intricate engineering phenomena [21,22,23]. Among the most precise and dependable machine-learning techniques are genetic programming, gene expression programming, and ANN [17]. The fundamental principle behind these algorithms is the development of models through the training of available datasets, allowing for a more dynamic and adaptable representation of complex relationships [24, 25].

Numerous studies have explored the utilization of ANN models in the field of ECCs. Various ANN models were utilized to forecast the mechanical characteristics of ECCs reinforced mostly with PVA and steel fibers [14, 26, 27]. These models exhibited commendable precision and the ability to generalize correctly. Nevertheless, the scope of these studies is confined to assessing the predictive accuracy of ANN models without delving into the interpretation of their outputs. Consequently, they offer minimal understanding of the input–output correlations, which is a cause for concern among researchers and engineers involved in the design of ECC. Additional sensitivity analysis should be undertaken using the established ANN model to accurately assess the impact of mixture design parameters on the development of mechanical characteristics in ECCs. Furthermore, prior research mainly concentrated on examining PE-ECC. Limited research has been conducted on using ANN for predicting mechanical characteristics of only PE fiber-based ECC.

Using an ANN model, this paper predicted the mechanical strength (e.g., CS, TS, and TSt) of PE-ECC. A comprehensive dataset containing 339 mixtures from published literature has been established with 12 influencing factors. The data are then arbitrarily divided into training, validation, and testing sets using proportions of 70% for training and 30% for validation and testing. This study confirmed the model's accuracy by evaluating the defects, MSE, RMSE, R2, and R. In addition, the sensitivity analysis was also carried out to evaluate each input parameter's contribution towards the PE-ECC prediction results.

2 Research significance

The PE- ECC has potentiality to improve the TS, TSt, Ductility, crack resistance, and toughness which makes the concrete more durable and more reliable to use in the structure. Some research novelty is mentioned in the below:

  • PE- ECC plays a pivotal role in sustainable construction practices – especially for engineers to design complex materials with high strain capacity, where the ML model will help to identify the optimized concrete mixtures.

  • A novel dataset is created to only focus on PE-ECC based concrete, which makes the predictive results more accurate, robust, and applicable to the industry.

  • The ANN models (i.e., optimizing different neurons and hidden layers) offer a powerful tool showing robust and accurate results.

  • The predictive model not only considered CS but also considered TS and TSt which are significant for the fiber-based concrete. Moreover, the input parameters for the fiber are carefully considered to get the appropriate results for TS and TSt.

  • The sensitivity analysis was also considered to observe the influential parameters in this study.

Later the methodology properly addressed the process of the influences of PE-ECC based concrete and this process can help to identify the proper mechanical strength of the concrete.

3 Methodology

ML techniques have recently been applied to simulate and predict challenging issues in science and engineering. One of the ML techniques, i.e., ANN, has been used to anticipate the behavior of numerous structural components and materials [28]. ANN model functions as a black box system (e.g., feed-forwardnet function to create a feedforward neural network) and configures training parameters (e.g., net.trainParam) using the Levenberg–Marquardt (LM) algorithm. The backpropagation (e.g., LM) is chosen among scaled conjugate gradient and resilient backpropagation. Six main processes are typically involved in the modeling of an appropriate ANN model: (1) data collection, analysis, and problem definition; (2) ANN model development; (3) architecture determination; (4) learning process determination; (5) training of the networks; and (6) testing of the trained network for validation [32].

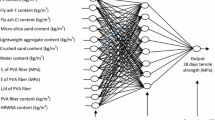
The main objective of the current work is to develop valuable ANN models for predicting PE-ECC mechanical properties (e.g., CS, TS, and TSt) by gathering databases from various mixed proportions based on previously published research. The model must next be trained and tested using input data to provide the desired model output. Fig. 1 illustrates the ANN model's methodology for determining various anticipated PE-ECC CS, TS, and TSt. This study examined the topic of Material selection and database analysis in Sect. 3.1, the theory of ANN in Sect. 2, the results and discussions of ANN models and the sensitivity analysis which is implemented in Sect. 4, and the conclusion is presented in Sect. 5.

Fig. 1
figure 1

Workflow of ANN Models for Predicting Mechanical Strengths of PE-ECC-Based Concrete

Full size image

3.1 Material selection and database analysis

The dataset utilized in this study comprises 339 samples of PE-ECC mixture that were gathered from various literature sources [13, 35,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53] [13, 54, 55].This dataset utilized fifteen features, comprising twelve input characteristics and three output features. Various features can influence the resulting mechanical property, regarded as the input variables [53]. The input variables consist of the following variables C/B, S/B, FA/B, GS/B, SF/B, SP/B, W/B, CA (day), AR, Df (mm), Lf (mm), Fv (mm). These twelve characteristics were equally considered to predict the CS, TS, and TSt of PE-ECC.

The statistical properties of the dataset hold higher significance in the context of ML models [29]. Figure 2 depicts a histogram of the PE-ECC, which graphically summarizes a univariate data set's distribution. Tables 1 and 2 summarizes the descriptive statistics for ECC's input, target, and output variables, encompassing measures such as mean, standard deviation, minimum, maximum, kurtosis, and skewness. This information is intended to facilitate understanding the data, which can also be related to Fig. 2. Skewness is a statistical metric that quantifies the degree of symmetry exhibited by the investigated variables.

Fig. 2
figure 2

Histogram of input and output data for PE-ECC

Full size image
Table 1 Existing literature for predicting fiber-based concrete
Full size table
Table 2 The statistical description of input variables in the CS, TS, and TSt databases
Full size table

On the other hand, kurtosis is a measure that determines if the dataset has heavy or light tails compared to a normal distribution. Figs. 3, 4, and 5 illustrate the correlation heatmap matrix of the input variables for CS, TS, and TSt, respectively. The heatmap's primary purpose is to uncover possible relationships between distinct variables and to comprehend their correlation. It also shows whether the input variable influenced the original variable selection. A correlation value of 0.90 to 1 implies that the variables have an influential positive or negative association [56]. Coefficients that fall between 0.50 and 0.70 indicate a robust correlation, whereas values below 0.25 represent a minimal relationship among the variables.

Fig. 3
figure 3

Heatmap depicting correlation matrix among C/B, S/B, FA/B, GS/B, SF/B, SP/B, W/B, CA (day), AR, Df (mm), Lf (mm), and Fv (mm) in predicting CS

Full size image
Fig. 4
figure 4

Heatmap depicting correlation matrix among C/B, S/B, FA/B, GS/B, SF/B, SP/B, W/B, CA (day), AR, Df (mm), Lf (mm), and Fv (mm) in predicting TS

Full size image
Fig. 5
figure 5

Heatmap depicting correlation matrix among C/B, S/B, FA/B, GS/B, SF/B, SP/B, W/B, CA (day), AR, Df (mm), Lf (mm), and Fv (mm) in predicting TSt

Full size image

Correlation coefficients within the range of ± 0.50 to 0.70, as well as those below ± 0.25, are indicative of a significant and weak association between the variables. Figure 3 shows the input variables, namely C/B, SF/B, and SP/B, which exhibit substantial positive correlation coefficients with CS with correlation coefficients of 0.43, 0.66, and 0.34, respectively. However, the FA/B and W/B correlation coefficients are negative, with values of -0.7 and -0.59, respectively, for the CS.

Figure 4 illustrates the input variables, specifically GS/B, AR/B, and Lf, that display noteworthy positive correlation coefficients with TS. The correlation coefficients for these variables are evaluated as 0.5, 0.34, and 0.35, in the given order. Similarly, Fig. 5 shows that the correlation coefficient for TSt exhibits positive values for FA/B, W/B, and AR of 0.48, 0.32, and 0.29, respectively. Conversely, C/B, SF/B, and SP/B show the negative correlation coefficients of 0.38, 0.43, and 0.37, respectively.

3.1.1 Artificial neural networks (ANN)

ANN are computational models that are inspired by the structure and function of biological neural networks in the brain [30, 57]. ANN models consist of interconnected units called artificial neurons, which can process and transmit signals to other neurons [33]. ANN can learn from data and perform various tasks such as classification, regression, clustering, dimensionality reduction, etc.

ANN can be trained using different algorithms, such as back-propagation, gradient descent, genetic algorithms, etc. [58, 59]. The training process involves adjusting the weights and biases of the artificial neurons to minimize the error between the actual output and the desired output. The error function can differ depending on the task, such as mean squared error, cross-entropy, etc. The training process can also use different techniques to improve performance and avoid overfitting, such as regularization, dropout, batch normalization, etc. [33].

The primary objective of this study was to construct an ANN model using the ANN toolbox in MATLAB R2017b software, and the LM algorithm was employed to validate the effectiveness of various neuron quantities. The LM algorithm utilizese random partitioning strategy to separate input and target vectors into three sets: training, validation, and testing. Modifying the respective proportions of these three sets has the potential to enhance the process of generalization marginally.

4 Results and discussions

4.1 Prediction and error analysis for ANN models

Tables 4, 5, and 6 show the performance of the proposed ML techniques for CS, TS, and TSt based on statistical analysis, respectively. We used four metrics to evaluate the accuracy of the ML techniques: R, R2, MSE, and RMSE. R and R2 measure how well the ML technique fits the data, while MSE and RMSE measure the average error between the actual and predicted values. A robust ML technique should have a high R and R2 value and low values for the other two metrics. Table 3 represents the statistical models to evaluate the ML models for the PE-ECC.

Table 3 Statistical models for the PE-ECC
Full size table

Network performance is evaluated by how low the error values are in the training process, with zero error indicating the best possible outcome. The network architecture also measures the correlation between the outputs and the targets using the coefficients of determination, or R-values. A high R-value (close to 1) means a strong and almost perfect correlation [17], while a low R-value (close to 0) means a weak and random correlation. The closeness of the model's training and testing results indicates the degree of overfitting of the model [18]. Overfitting is a problem that occurs when the model learns too much from the training data and fails to generalize well to new data. Therefore, evaluating the overfitting of the ML techniques is an important aspect of their performance. The optimal network configuration was selected based on a dual-criteria approach encompassing the MSE and the R-values.

With the optimal network configuration now established, we apply our rigorously validated model to the critical task of predicting the mechanical properties—CS, TS, and TSt—of PE-ECC. This step is pivotal, as it not only assesses the model’s predictive power but also underscores its practical relevance in advancing material science.

4.2 Strength prediction results

4.2.1 Prediction of compressive strength (CS)

The statistical analysis results for the CS using the proposed ML techniques are displayed in Table 4. This study involved the development of seven ANN models with varying numbers of hidden neurons to forecast the CS of PE-based ECC. The R2-values for all hidden neurons in the system ranged from 0.85 to 0.96, as observed in Table 4. The ANN model with ten hidden neurons achieved the highest accuracy of 0.96, followed by models with 8, 14, 12, 6, and 4 hidden neurons in descending order. The ANN2, ANN4, ANN6, ANN8, ANN10, ANN12 and ANN14 represents the neural networks 2, 4, 6, 8, 10,12, and 14 respectively. The model with two hidden neurons obtained the lowest accuracy of 0.85. The regression plot in Fig. 6 illustrates the performance of the best ANN model with ten hidden neurons, showing a high R-value of 0.97 for all stages (e.g., training, validation, testing, and total). These results verify the accuracy and reliability of the model in estimating the CS of PE-ECC. Figure 7 presents the performance of the trained ANN model, with some errors observed but overall satisfactory validation outcomes, including a value of 90.123 and an optimal epoch of 31. Furthermore, Fig. 8 displays an error histogram illustrating the distribution of errors across different CS levels, with an error range of -26.62 to 29.11 and varying numbers of instances for the training, validation, and testing data.

Table 4 Compressive strength of ECC with various hidden neurons
Full size table
Fig. 6
figure 6

Regression plot for CS of PE-ECC

Full size image
Fig. 7
figure 7

Performance Plot for CS of PE-ECC

Full size image
Fig. 8
figure 8

Error Histogram plot for CS of PE-ECC

Full size image

Based on the comparison of all seven models in Table 4, the model with twelve hidden neurons exhibited the lowest RMSE value of 7.8 for testing data, although not for training data of 8.62. A similar situation occurred for the model with 14 hidden neurons. Consequently, the model with ten hidden neurons achieved the best accuracy in terms of RMSE values (training- 8.44, testing- 8.62). Figures 9, 10, and 11 depict the error values between the actual and predicted CS for the training, validation, and testing data using the ANN models. These results indicate that the number of hidden neurons significantly influenced the prediction accuracy, as reflected by the lower mean square error values throughout the training, validation, and testing stages. Taking into consideration these findings, it can be concluded that the ANN model with ten hidden neurons exhibits high accuracy in predicting CS, owing to its low error values.

Fig. 9
figure 9

Error plot between actual and predicted training datasets for predicting the CS

Full size image
Fig. 10
figure 10

Error plot between actual and predicted validation datasets for predicting the CS

Full size image
Fig. 11
figure 11

Error plot between actual and predicted testing datasets for predicting the CS

Full size image

Table 2 presents a comparison between the experimental findings and the prediction model based on ANN. The deviation between the experimental mean CS and the predicted mean CS was approximately 1.591 MPa, representing a mere 1.42% discrepancy from the experimental mean CS value.

Moreover, the comparison of the mean experimental target and the mean predicted outputs revealed negligible differences (errors) compared to the individual experimental and predicted strength values.

4.2.2 Prediction of tensile strength (TS)

The present study applied the same modeling and analysis methods utilized for predicting CS values of PE-ECC to forecast the TS. However, in order to enhance the accuracy of the ANN models for TS, a total sample size of 325 was employed. The results detailing the performance of the ANN model with various hidden neurons are summarized in Table 5. According to the R2-values presented in the table, the accuracy of the ANN models varied from 0.79 to 0.94 with different numbers of hidden neurons. Notably, the model with 10 hidden neurons demonstrated the highest accuracy of 0.94, followed by the models with 6, 8, 12, 14, and 4 hidden neurons in descending order. Conversely, the model with two hidden neurons achieved the lowest accuracy of 0.79. The regression plot displayed in Fig. 12 presents the results obtained from the most accurate ANN model (e.g., ten hidden neurons), revealing R-values of 0.97, 0.94, 0.94, and 0.96 for the training, validation, testing, and total stages, respectively. These values indicate that the model provides reliable and accurate predictions of TS for PE-ECC. Figure 13 depicts the error values between the actual and predicted TS for the training, testing, and validation data using the best ANN model, showcasing satisfactory results with a value of 1.2522 and an optimal epoch of 170. Additionally, Fig. 14 illustrates the error histogram with 20 bins for the training, testing, and validation data at different TS levels, employing distinct colors. The histogram demonstrates that the error range spans from -5.032 to 5.038, with the number of samples for the training, testing, and validation data approximately totaling 70, 85, and 95, respectively.

Table 5 Tensile strength (TS) of ECC with various hidden neurons
Full size table
Fig. 12
figure 12

Regression Plot for TS of PE-ECC

Full size image
Fig. 13
figure 13

Performance Plot for TS of PE-ECC

Full size image
Fig. 14
figure 14

Error Histogram Plot for TS of PE-ECC

Full size image

The performance of the ANN models with diverse hidden neurons in predicting TS is presented in Table 5. The model with ten hidden neurons yielded the lowest RMSE value of 0.95 for training, as well as the second lowest RMSE value of 1.29 for testing. While the model with 6 hidden neurons exhibited a lower RMSE value for testing of 1.16, it also yielded a lower R2 value and a higher RMSE value for training 1.37. Thus, the model with ten hidden neurons emerged as the most accurate and consistent model when considering the RMSE value. Figs. 15, 16, and 17 showcase the errors between the target and predicted values across training, validation, and testing data, respectively, employing the ten hidden neurons ANN model. The impact of the number of hidden neurons on prediction accuracy is evident from the lower MSE values observed in all stages when utilizing the best ANN model. Collectively, these findings lead to the conclusion that the ANN model featuring ten hidden neurons offers high accuracy in predicting TS due to the low error values.

Fig. 15
figure 15

Training datasets Plot for TS of PE-ECC

Full size image
Fig. 16
figure 16

Validation datasets Plot for TS of PE-ECC

Full size image
Fig. 17
figure 17

Testing datasets Plot for TS of PE-ECC

Full size image

Table 2 presents a comprehensive comparison between the input parameters and the TS values ascertained experimentally and those predicted by the ANN. The mean predicted TS exhibited a high degree of congruence with the mean experimental TS, deviating by a marginal 0.475 MPa. This deviation represents a negligible 5% of the mean experimental TS, underscoring the precision of the ANN model. Notably, the percentage error observed when comparing the mean experimental target to the mean predicted output was substantially lower than the error margins recorded for individual samples, indicating the model’s robust predictive capability.

4.2.3 Prediction of tensile strain (TSt)

The same processes for CS and TS prediction were used for the TSt prediction of PE-ECC but with 318 samples. Table 5 summarizes the results of the ANN models with different hidden neurons for TSt. The best model was the one with 12 hidden neurons, which had an R2-value of 0.93 and an R-value of 0.96 for the total data, as shown in the regression plot in Fig. 18. The error values for the training, testing, and validation data using the best model are shown in Fig. 19, which also shows a satisfactory validation result with 0.8413 and an optimal epoch of 81. The error histogram with 20 bins for the different data sets at different TSt levels is displayed in Fig. 20, which shows a low error range of -2.93 to 3.106, and the number of samples for the training, testing, and validation data was about 75, 85, and 98, respectively.

Fig. 18
figure 18

Regression Plot for TSt of PE-ECC

Full size image
Fig. 19
figure 19

Performance Plot for TSt of PE-ECC

Full size image
Fig. 20
figure 20

Error Histogram Plot for TSt of PE-ECC

Full size image

Table 6 summarizes the performance of the ANN models with different hidden neurons for TSt prediction. The best model was the one with 12 hidden neurons, which had the smallest RMSE value, 0.84 for training and 0.92 for testing. Therefore, this model achieved the best accuracy and consistency in terms of RMSE value compared to any other model. Figures 21, 22, and 23 show the error values between the target and predicted values for the training, validation, and testing data using the best ANN model. The prediction accuracy was influenced by the number of hidden neurons, as indicated by the lower MSE values for all stages using the best ANN model. These results suggest that the ANN model with 12 hidden neurons had a high accuracy for predicting TSt due to the low error values.

Table 6 Tensile strain of ECC with various hidden neurons
Full size table
Fig. 21
figure 21

Training datasets Plot for TSt of PE-ECC

Full size image
Fig. 22
figure 22

Validation datasets Plot for TSt of PE-ECC

Full size image
Fig. 23
figure 23

Testing datasets Plot for TSt of PE-ECC

Full size image

According to Table 2, the difference between the mean experimental and mean predicted TSt is 0.31 MPa, representing a mere 6.11% of the experimental TSt value. The difference percentage between the mean experimental target and the mean predicted outputs was much smaller than the difference values for each individual sample.

4.3 Sensitivity analysis

A sensitivity study was conducted to assess the relative impact of each input parameter on the prediction of CS, TS, and TSt of PE-ECC. Since each input parameter substantially impacts the forecast of the outcome, it is imperative to have a comprehensive understanding of the efficacy of each particular input parameter. Figures 24, 25, and 26 depict the effectiveness of input parameters predicting the CS, TS, and TSt, respectively. Figure 24 illustrates that the main variables influencing the CS of PE-ECC are C/B (95%), S/B (85%), GS/B (43%), SF/B (88%), SP/B (86%), W/B (88%), CA (61%), AR (91%), Lf (92%), and Fv (95%), respectively. Nevertheless, the remaining input factors had a relatively minor contribution to the forecast of CS of PE-ECC, with FA/B (27%) and Df accounting for (8%). Similarly, Figs. 25 and 26 illustrate the influence of input parameters on the TS and TSt. The F/B shows less effect for the TS and TSt however, the C/B and S/B have a similar approach. The Df is the lowest influence parameter for the CS, TS, and TSt. During the experimental phase, a significant advancement was noticed in which the concentration of CS exhibited an increase in response to variations in CA (days) and mixture parameters. To ascertain the individual impact of each parameter on the projected outcome, Eq. 2 was obtained from a of literature [31]. In order to utilize the equation, all data pairs were employed, with each data pair being applied subsequently to form the data array xi.

$$X_i=\left\{X_{i1},X_{i2},X_{i3},........,X_{in}\right\}$$
(1)
Fig. 24
figure 24

The impact of input parameters on compressive strength

Full size image
Fig. 25
figure 25

The impact of input parameters on tensile strength

Full size image
Fig. 26
figure 26

The impact of input parameters on tensile strain

Full size image

The equation represents the relative influence rij between datasets xi and xj.

$$r_{ij}\frac{\displaystyle\overset k{\underset{n=1}{\sum X_{in},X_{jn}}}}{\sqrt{\displaystyle\overset k{\underset{n=1}{\sum X_{in}^2}}}\sqrt{\displaystyle\overset k{\underset{n=1}{\sum X_{jn}^2}}}}$$
(2)

Armed with the insights gleaned from our comprehensive sensitivity analysis, we are now poised to encapsulate the overarching conclusions drawn from our extensive study.

5 Conclusion

This study presents the development of ANN models designed to estimate the mechanical properties (e.g., CS, TS, and TSt) of the PE-ECC. The models were developed using datasets comprising 339, 325, and 319 respectively test results for CS, TS, and TSt, respectively. To predict the CS, TS, and TSt values of the PE-ECC mixtures, seven distinct ANN architectures with varying numbers of hidden neurons (e.g., 2, 4, 6, 8, 10, 12, and 14) were evaluated. The ANN model featuring 10 hidden neurons yielded the most accurate predictions for CS and TS, while the model with 12 hidden neurons was superior for TSt prediction. Performance metrics (e.g., R, and R2, MSE, RMSE) were employed to finalize the ANNs for training, validation, and testing of the PE-ECC samples. The outcomes of this investigation enable the following conclusions:

  • The ANN model with 10 hidden neurons demonstrated high predictive accuracy for the CS of PE-ECC, with an R2 of 0.94 for training, and 0.96 for both validation and testing phases. The RMSE was 9.49 for training, 8.44 for validation, and 8.62 for testing, indicating the model’s precision across different evaluation stages. The relative error for CS was as low as 1.42%, highlighting the model’s exceptional precision. To enhance the model's performance, exploring advanced regularization techniques and expanding the training dataset is recommended.

  • The ANN model with 10 hidden neurons confirmed its efficacy in predicting the TS of PE-ECC, with an R2 of 0.88 for training and testing, and 0.94 for validation. The RMSE values were 1.12 for training, 0.95 for validation, and 1.29 for testing, indicating a consistent predictive performance. The model achieved a relative error of 5% for TS, showcasing its accuracy. Addressing the RMSE disparity observed between validation and testing may involve refining data preprocessing and feature engineering methods.

  • The ANN model with 12 hidden neurons showcased robust capabilities for predicting the TSt of PE-ECC, achieving an R2 of 0.92 for training and testing, and 0.93 for validation. The RMSE remained consistent at 0.92 for training and testing, with a lower 0.84 for validation. The relative error for TSt was 6.11%, further confirming the model’s reliability. Investigating factors during the validation phase that contributed to the lower RMSE could provide insights to optimize model accuracy.

  • Sensitivity analysis indicated the differential impact of input parameters on the prediction of CS, TS, and TSt. Parameters such as C/B, SF/B, Lf, and Fv were highly influential for CS, while FA/B and Df had lesser effects. For TS and TSt, parameters like C/B, W/B, and Lf were critical. This underscores the importance of a comprehensive understanding of each parameter's influence to enhance predictive models.

This study’s comprehensive analysis of ANN models underscores the importance of specific input parameters and model configurations in accurately predicting the mechanical properties of PE-ECC. The minimal prediction errors across CS, TS, and TSt validate the models’ effectiveness and suggest avenues for model refinement, highlighting the potential for ANN models in material property estimation. Future research should delve deeper into the interaction between input parameters and model structure to refine the accuracy and utility of ANN predictions in material properties. This exploration is crucial for aligning with the broader objectives of sustainability and low-carbon initiatives in civil engineering, underscoring the pivotal role of sophisticated ANN models in realizing these environmental goals.