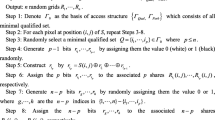On Multi-image Random Grids by Arbitrary Transformations

Abstract

Random grids are a method for visual secret sharing, whereby a secret image is encoded into a number of shares, each of which is maximally entropic. There has been growing interest in hiding multiple images in a scheme, such that additional images are revealed by stacking the shares in different ways. This paper proposes a metaheuristic method for generating schemes that allow for a wide range of transformations, or even combinations thereof, to reveal an arbitrary number of secret images. Up to 10 multi-secrets are shown in this paper, as well as hiding multiple secrets in a general access structure. To remove noise from these schemes an algorithm is proposed to extract the information from the noise, and in all cases, relative contrasts are given. In one example, six images are hidden in two shares, such that the mean relative contrast under OR-stacking is 0.152, under XOR-stacking 0.278, and with noise removed, it is 0.74. In an example hiding 10 images in two shares, the values are respectively 0.136, 0.206 and 0.679, respectively.

1 Introduction

Presently, technologies that serve as a defense against unrestricted data sharing and communication are gaining importance. With this in mind, cryptography plays an increasingly critical role. Visual secret sharing is a specialized method dedicated to the encryption of visual information for human comprehension. This form of data protection has a storied history within the scientific community.

Shamir proposed Secret Sharing (SS) as a cryptographic paradigm, producing individually unconditionally secure shares of the plaintext [1]. For images, Kafri and Keren proposed Random Grids [2]. Each grid is a share of a black and white secret image, and this can be decoded with XOR or by physically stacking the shares (i.e., the OR operation). This was the first form of cryptography with Human Visual Decryption.

In threshold secret sharing schemes, n shares are generated, requiring at least k shares to reassemble the plaintext. None of the shares contain any information about the plaintext, rendering it immune to an adversary with unbounded computation. Despite this, creating multiple shares comes at the cost of additional storage. Thus, researchers have been exploring solutions to share multiple secret images in one [3].

This work enables revealing multiple secret images from a single scheme by applying different transformations to the first share relative to the others when stacking. The specific transformations used include rotation, translation, flipping, projecting sides, distance morphing, and more, as categorized in Table 1.

Table 1 List of share transformation considered in this study

Rotation by non-right angles is a key capability, as this avoids distortion of the rectangular shares. Translation involves shifting the first share, either with resizing to fit the overlap or clipping off any part that goes beyond the edge. Flipping horizontally or vertically is another simple transformation.

More advanced techniques like projection and distance morphing distort the image in exchange for greater hiding capacity. Projection lifts two adjacent sides partially up off the stack, revealing a hidden image in the created gap. Distance morphing shifts pixels within the share inward or outward from a central point, according to their distance.

The practical implication is that by allowing such a wide range of affine and non-affine transformations, multiple images can be encoded into a scheme and selectively revealed. This gives more flexibility compared to prior works that rely on flipping, rotation, or translating only. To accomplish this, Simulated Annealing (SA) [4] is proposed, and has been shown to allow not only for arbitrary share transformations but General Graph Access Structures (GGAS) and multi-secret sharing, and even schemes that apply varying levels of importance (weights) to different reconstructions.

Furthermore, to address the issue of poor visual quality inherent in these multi-image schemes, we propose a novel algorithm designed for the denoising of shared stacks, thereby more accurately revealing the original shared image. Numerous existing deep learning techniques employ autoencoders—first introduced by Rumelhart et al. [5]—for denoising purposes, notable examples being those by Kulkarni et al. [6] and Yasenko et al. [7]. In a different approach, the Noise2Void algorithm by Krull et al. [8] operates on singular noisy images without the need for autoencoders. While these methodologies have been validated on images with legible content obscured by noise, they are unlikely to be suitable for images with the level of extreme noise in the reconstructions presented in this study.

The major contributions of this paper are:

• Annealed Random Grids (ARG) with objective function, nearest neighbour algorithm and cooling schedule.

• Robust schemes with general graph access, multi-secret encoding, or both.

• Visual Secret Sharing (VSS) Extractor, a noise reduction algorithm for ARG and visual secret sharing in general.

The relevant notation specific to secret sharing and image transformation is below:

• $\Gamma ,\Gamma_{qual} ,\Gamma_{forb}$: An access structure along with qualified and forbidden subsets within that structure.

• $(w,h)$: The width and height of an image

• $k,n$: The threshold and total number of shares in a scheme.

• ${\mathcal{S}}$ and ${\mathcal{S}}\prime$: An original secret image and its reconstruction.

• ${\mathcal{H}}_{i} ,i \in \{ 1,...,n\}$: The shares.

• $\alpha$: Relative contrast with a secret image.

• ${\mathcal{T}}^{w},{\mathcal{T}}^{b}$: Transmission rates for (original) white and black pixels, respectively. Note that $\alpha = {\mathcal{T}}^{b} - {\mathcal{T}}^{w}$.

• $\sigma$: The number of images being encoded into one scheme.

• $\Psi_{i}$: A transformation of one share relative to another.

• $\tau$: The amount by which to apply a given transformation (or $\emptyset$ if not applicable).

• $T = (\Psi_{0} ,\emptyset ),(\Psi_{{i_{2} }} ,\tau_{2} ),...,(\Psi_{{i_{\sigma } }} ,\tau_{\sigma } )$: The list of transformations being applied, per secret image.

• $\left\{ {(\Psi_{{i_{1} }} ,\tau_{{i_{1} }} ),(\Psi_{{i_{2} }} ,\tau_{{i_{2} }} ),...} \right\}$: A set of multiple transformations applied for the encoding of one image (applied from left to right in the notation).

The remainder of this paper is structured as it follows: Sect. 2 reviews prior visual secret sharing work. Section 3 details ARG; it begins with the SA setup and objective function, then gives details about the available share transformations. Section 4 shows the visual results and provides a security analysis of the proposed method using Just-Noticeable-Difference (JND) theory. Section 5 provides a comparative analysis of this method with prior studies, and finally Sect. 6 concludes the study.

2 Background

In the scheme of Shamir [1], the plaintext is split into shares, each containing no information about the plaintext. This was as opposed to conventional cryptography, in which plaintext is obscured through confusion and diffusion. SS guarantees that the secret cannot be obtained from fewer than the threshold number of shares. Its strength also lies in the ability to form access structures, allowing only pre-determined share combinations to reveal the secret.

Based on this, a method for images was introduced by Kafri and Keren [2], in what they proposed Random Grids (RG) to share images securely. Each grid represents a share of a binary secret image, and by applying XOR, the secret is revealed. Grids can be printed onto transparent sheets and stacked to reveal the secret, making this the first form of cryptography with decryption using human vision alone, hence called Visual Secret Sharing (VSS). Similar to RG, Naor and Shamir [9] introduced Visual Cryptography (VC), where shares appear similar to random grids, but are constructed with basis matrices, i.e., the rulebook [5]. However, this comes with the cost of increased share size, known as pixel expansion.

Since then, there has been a surge of interest in RG, especially since Chen and Tsao [27] and Wu and Sun [28] constructed threshold schemes without rulebooks [6, 7]. Furthermore, general access structures have been shown, notably by Shyu [31], with quality improved by others, such as Liu et al. [13], allowing weighted reconstructions [8, 9].

Gurung et al. [14] developed Circular RG, demonstrating three secret images in two circular shares [10]. They first created a random master share, which was reshaped into a circle. This was XOR'd with the first secret image, and the first share was rotated by the first requisite angle and XOR'd with the second secret. The process continued until a sequence of complementary shares was created, which were merged into a final circular grid that was rotated with respect to the first to reveal the secrets at the correct angles.

Shyu and Jiang [12] proposed using integer programming to generate (k, n, s)-VSS schemes, where s is the number of secrets [8]. Each successive secret is revealed by stacking another share, and certain stack sizes can be forbidden. There are not two, but 2 s basis matrices (hence requiring a rulebook), one for each combination of binary pixel values for the set of secret pixels at a respective position. A (2, 4, 2) scheme is shown, but with a pixel expansion above 20. Indeed, they conceded unwieldy pixel expansion as scheme sizes increase.

Tsao et al. [15] proposed a Multi-Secret General Access Structure RG Method, highlighting the importance of general access structures in granting the dealer control over who can see the secrets [11]. Similar to this, weak access structures are recommended as they offer greater flexibility in generating a desired structure. However, the encoding results have a contrast of at most 1/13, even with only one secret.

Not all multi-secret sharing is based on RG, as Lee et al. [16] developed a (2, 2)-VC approach for revealing two secret images [12]. They refer to their method as VC, as it uses a rulebook of four-bit binary vectors, with possible combinations corresponding to pixel block combinations in the two images. The method uses an extended-VSS approach to watermark shares with grayscale cover images. Unlike most other extended methods, the cover images are still visible in the reconstructions. The additional secret image is revealed by rotation by a right angle, and one benefit is perfect black pixel reconstruction.

More recently, Chang et al. [17] proposed a scheme with two random grids to encode up to six images [13]. They did this by setting the first share as random and reshaping the second share to encode multi-secrets. Intriguingly, they reported that reshaping can physically take place by folding a share into a cylinder. Two of these authors later developed a method in Huang et al. [18] to encode multiple secrets into meaningful shares (extended VSS), and they demonstrated two images in (n, n) schemes [14].

A scheme based on Non-Monatomic Thresholds was given by Wu et al. [19], where stacking different numbers of shares reveals different secret images (or no secret image) using XOR [15]. They demonstrated up to two secrets when stacking two, three, or four shares, with high contrast results. Being a VC method, it has pixel expansion.

As in the present work, metaheuristics have been used in a small number of studies, such as Prema and Natarajan [20], who used it on the pixel locations in stereo-images concealing visual cryptography shares [16], and Chiu and Lee [21], who used simulated annealing on pixel-expansion-free visual cryptography, taking both contrast and pixel blackness as metrics in the algorithm [17].

3 Material and Methods

3.1 Simulated Annealing

Here we present the details of the proposed system, namely the relative share transformation, the simulated annealing initialization, the cooling schedule and nearest neighbour, the objective function and finally the noise removal from the computational reconstructions.

SA is an ideal single-agent metaheuristic suitable for large search spaces [4]. It is modeled after the heating and cooling of metal to optimize its properties. SA navigates the search space by accepting random moves that may increase the objective function, but with decreasing probability as the 'temperature' decreases. This enables the exploration of a broader region initially to avoid local optima, before exploitation dominates. The process is summarised as follows:

Algorithm 1: General Simulated Annealing Algorithm

This process is well-suited to evolving random grid schemes that can reveal multiple secret images under transformations. The search space is extremely large, comprising all combinations of pixel values across all shares. By accepting uphill moves initially, the algorithm is able to escape local optima where contrast constraints are met for some qualified subsets, but not others. The cooling drives the candidate solutions toward optimising the objective for all desired images and transformations. The specific initialisation, cooling schedule, and neighbour generation used in the SA implementation are detailed in this section.

3.2 Relative Contrast

Relative contrast ($\mathrm{\alpha }$) measures the visual quality of a revealed secret image compared to the original. It is defined as the difference between the transmission rates of the original black (b) and white (w) pixels, i.e.,

$$\mathrm{\alpha }= {\mathcal{T}}^{b}- {\mathcal{T}}^{w}$$

(1)

This is the proportion of pixels revealed as white in the decoding. For original white pixels, this should be high to preserve brightness. For original black pixels, it should be low to keep them dark. A higher $\mathrm{\alpha }$ indicates the reconstructed secret more closely resembles the original. Contrast is measured for each qualified subset that reveals an image. Maximizing $\mathrm{\alpha }$ across all transformations and qualified sets is a key aim of the optimisation.

3.3 Relative Share Transformation

In this study, a transformation of one share relative to another is denoted $\Psi_{i} ,i \in \{ 0,...,12\}$, where the transformations, i, are listed in Table 1.

To encode multiple secret images, let $\sigma \ge 2$ and $T = (\Psi_{0} ,\emptyset ),(\Psi_{{i_{2} }} ,\tau_{2} ),...,(\Psi_{{i_{\sigma } }} ,\tau_{\sigma } )$. Furthermore, there is a matrix of fractional weights, $W = \{ 0,...,1\}^{{\sigma \times \left| {\Gamma_{qual} } \right|}}$, indicating the importance (hence resulting quality when reconstructed) of the transformation in the objective function for a given secret image in a given qualified subset (similar to the idea of weighted reconstructions proposed in [9], for example. Unless otherwise indicated, all values in W are set to 1, giving all reconstructions equal importance.

The parameter $\tau_{i} ,i = 1,...,\sigma$ is measured in degrees for rotation, pixels if $\left| {\tau_{i} } \right| \ge 1$ or according to the fraction of the share's width or height if $\left| {\tau_{i} } \right| < 1$ (for example, if $h = 500$ pixels and $t_{i} = (\Psi_{2} , - 0.4)$, ${\mathcal{H}}_{1}$ shifts 200 pixels upward.). Each $t_{i} \in T$ applies to ${\mathcal{H}}_{1}$ only and is associated with each ${\mathcal{S}}_{i} ,i = 1,...,\sigma$.

As $t_{1}$ applies to the first share in the respective qualified subset (revealing the first image for that subset), it is not associated with a transformation. Note that there are two forms of horizontal and vertical translation (shifting). The first resizes ${\mathcal{S}}_{i}$ to fit in the area of overlap between shares, whereas the other clips the image, with the clipped part lost. Some examples are shown in Table 2, starting with the original image.

Table 2 Example transformations of the first share in a multi-secret random GS

This is therefore the first multi-secret VSS proposal allowing rotation of rectangular shares by non-right angles, avoiding distortion, such as that seen in Chen and Li [18].

Validity of random grid schemes is defined in terms of contrast and security. Given the stochastic nature of the proposed method, the latter cannot be proven in the usual ways, e.g. as originally shown in [2] and the various adaptations explored in Sect. 2. However, in Sect. 4, the theoretical limit to visual perception is discussed based on JND theory, so the stopping criteria cannot be met at least until the algorithm results in invisibility of the secret(s) in $\Gamma_{forb}$.

3.4 Simulated Annealing Initialization

Let the initial candidate solution be,

$$C_{0} = \overbrace {{\left( {random([0,1])} \right)^{w \times h} ,...,\left( {random([0,1])} \right)^{w \times h} }}^{n}$$

(2)

Before the main loop, let current candidate $C_{curr} \leftarrow C_{0}$. (Note that the candidate size is $nwh$ or $3nwh$ for colour images).

The initial temperature is $temp_{0} = 1$ and the final temperature $temp_{freeze} = 0$.

The neighbour distance (see Algorithm 1) $\delta$, which determines how far the randomly selected neighbour is from the current candidate, is also constant. Based on experimentation with convergence times, $\delta = 3$ is effective. The number of iterations depends on scheme complexity and values selected to obtain the results in Sect. 4 were based on experimentation.

3.5 Cooling Schedule and Nearest Neighbour

The temperature reduces linearly:

$$temp = 1 - \frac{iter}{{iter_{\max } }}$$

(3)

where $iter$ is iteration number. At each iteration, this increments and the new candidate is given by Algorithm 1.

Algorithm 1: Nearest Neighbour Construction

This algorithm swaps pixel values at random locations across shares in $C_{curr}$ with their neighbours. The probability of accepting $C_{new}$ is as follows, with non-zero probability of accepting worse schemes fostering exploration of the search space.

$$P(E_{curr} ,E_{new} ,T) = \left\{ {\begin{array}{*{20}c} {e^{{\frac{{E_{curr} - E_{new} }}{T}}} } & {{\text{if }}E_{new} < E_{curr} } \\ 1 & {{\text{otherwise}}} \\ \end{array} } \right.$$

(4)

where the E values are the energy in SA, i.e., the cost of the candidate.

3.6 Objective Function

$C_{curr}$ and $C_{new}$ are, in turn, taken as input into the objective function. It relies on two equations to calculate $\Delta_{1}$ and $\Delta_{2}$, which are respectively the energy decrease based on similarity between ${\mathcal{S}}$ and ${\mathcal{S}}\prime$ after stacking, and increase based on similarity between individual shares and ${\mathcal{S}}$. The former aims to satisfy the contrast constraint and is defined as:

$$\Delta_{1} = \left( {\sum\limits_{x = 1}^{w} {\sum\limits_{y = 1}^{h} {\sum\limits_{z = 1}^{c} {\left| {{\mathcal{S}}^{xyz} - \left( {{\mathcal{S}}\prime } \right)^{xyz} [q]} \right|} } } } \right)^{3}$$

(5)

where q is the index of the respective qualified subset. The absolute difference between secret and reconstruction is cubed, as it has been shown experimentally to converge faster. The latter aims to satisfy the security constraint and is defined as:

$$\Delta_{2} = \sum\limits_{i = 1}^{n} {\sum\limits_{x = 1}^{w} {\sum\limits_{y = 1}^{h} {\sum\limits_{z = 1}^{c} {\left| {{\mathcal{S}}^{xyz} - C^{i} [x,y,z]} \right|} } } }$$

(6)

This measures the absolute difference between the secret image and each share packaged into the candidate, looking at every pixel in each colour channel, for each share. Algorithm 2 summarises the objective function.

Algorithm 2: Objective Function

The use of Eq. (6) drives energy downward based on Euclidean distance between each share and ${\mathcal{S}}$. This helps maintain security, deterring shares from leaking the secret. Further note that to derive multi-secret schemes under different transformations of ${\mathcal{H}}_{1}$, it is sometimes necessary to apply the respective transformation to ${\mathcal{S}}$ before calculating the Euclidean distance. Such transformations are those that distort the image in some way, as indicated in Table 2, and without this distortion, contrast could not be meaningfully measured.

3.7 Noise Removal from Computational Reconstructions

Images encoded with VSS can be decoded physically (simulated using OR) or computationally (with XOR). In multi-secret schemes, additional quality is lost with more information being stored in the scheme.

There are many existing image noise reduction algorithms, such as that by Hasanzadeh and Daneshvar [19], that analyze properties of block pixel patterns to smooth out or eliminate redundant pixels, but to the authors’ knowledge, there no such algorithm suited to the extreme noise in VSS reconstructions.

Algorithm 3, termed VSS Extractor, is proposed to reduce noise in RG XOR stacks, and the combined operation is denoted $\oplus^{C}$. It homogenizes regions of similar transmission rate. Results in Sect. 4 show that this does not necessarily increase contrast but enables thresholding of the result to produce a binary image closely approximating the original. The combined operation of XOR, cleaning and thresholding is denoted $\oplus^{CT}$.

Algorithm 3: VSS Extractor

This generates successively larger maps of colour values surrounding each pixel, out to a distance of $\eta$, and records the mean within the respective map. The means are then weighted to favour the maps in closest proximity and the resulting weights averaged to estimate the pixel value. Each pixel in the reconstruction is processed this way to form a density map of all weighted means, and its contrast enhanced by comparing each value to $\theta$. The pixel is brightened or darkened based on the comparison. Some results are shown in Table 3, with increasing distance.

Table 3 Results of noise reduction from RG decoded images

Based on this, $\eta = 10$ is used in this study, as it produces clearer reconstructions than $\eta = 5$, but avoids exponentially increased execution times. The threshold depends on image type and can easily be calibrated to produce a cleaner reconstruction.

4 Results

The test image sets used in this section are given in Figs. 1, 2 and 3, each sized to $200 \times 200$ pixels (unless otherwise stated). Note that image set 2 can be extended to the full alphabet.

Fig. 1

Image set 1 (A1 to A6)

Fig. 2

Image set 2 (B1 to B6)

Fig. 3

Image set 3 (C1 to C6)—$100 \times 200$ pixels

4.1 Multi-secrets Along Graph Edges

As the edges in the graph representation of a scheme represent qualified subsets of connected nodes, the prior examples attach the same secret image to each edge. However, if a different image is specified in the objective function for $X \in \Gamma_{qual}$, multi-secret encoding is accomplished on graph edges.

The algorithm constructed the shares and subsets of a (2, 5)*-RG scheme, using Images A1 to A4. This is a strong access structure in which there are five shares, two of which need to be combined, and any subset with more than three shares is forbidden, as is any subset not including the first share [20]. The shares, XOR-stacks and results of VSS Extractor are shown in Fig. 4, but for brevity, only shares 1 and 2 are shown.

Fig. 4

(2, 5)* general access RG scheme. a ${\mathcal{H}}_{1}$, b ${\mathcal{H}}_{2}$, c ${\mathcal{H}}_{1} \oplus {\mathcal{H}}_{2}$, d ${\mathcal{H}}_{1} \oplus {\mathcal{H}}_{3}$, e ${\mathcal{H}}_{1} \oplus {\mathcal{H}}_{4}$, f ${\mathcal{H}}_{1} \oplus {\mathcal{H}}_{5}$, g ${\mathcal{H}}_{1} \oplus^{CT} {\mathcal{H}}_{2}$, h ${\mathcal{H}}_{1} \oplus^{CT} {\mathcal{H}}_{3}$, i ${\mathcal{H}}_{1} \oplus^{CT} {\mathcal{H}}_{4}$, j ${\mathcal{H}}_{1} \oplus^{CT} {\mathcal{H}}_{5}$, k ${\mathcal{H}}_{2} \oplus {\mathcal{H}}_{3}$, l${\mathcal{H}}_{3} \oplus {\mathcal{H}}_{4}$

The individual contrasts are summarised in Table 4. Contrasts of two forbidden stacks are also given.

Table 4 Relative contrasts in a binary (2, 5)* image-per-edge RG scheme

Forbidden stack contrasts are non-zero but negligible. As shown using JND Theory in Sect. 4.3, security is maintained.

4.2 Multi-secrets with Share Transformations

In Fig. 5, images A1 to A5 are encoded into a (2, 2)-RG scheme under the following transformations involving translation and rotation. It evolved within 40,000 iterations.

$$\begin{array}{*{20}l} {} \hfill & {t_{1} = (\Psi_{0} ,\emptyset ),} \hfill \\ {} \hfill & {t_{2} = (\Psi_{3} ,90),} \hfill \\ {} \hfill & {t_{3} = (\Psi_{1} ,0.2),} \hfill \\ {} \hfill & {t_{4} = (\Psi_{2} ,0.2),} \hfill \\ {} \hfill & {t_{5} = (\Psi_{5} ,\emptyset ).} \hfill \\ \end{array}$$

Fig. 5

Five-image (2, 2)-RG scheme. a ${\mathcal{H}}_{1}$, b ${\mathcal{H}}_{2}$, c–g $\otimes$-stacks. h–l $\oplus$-stacks. m A sample $\oplus^{C}$ stack. n–r $\oplus^{CT}$-stacks

It is clear that translation produced lower contrast than other transformations. This is due to losing information through resizing, particularly deleterious in OR-stacks. Contrasts are summarised in Table 5.

Table 5 Relative contrasts in binary (2, 2) 5-image RG

Let us now consider six images, C1 to C6, encoded into (2, 2)-RG, shown in Fig. 6, with OR-stacks omitted for brevity. The scheme evolved within 50,000 iterations (Table 6).

$$\begin{array}{*{20}l} {} \hfill & {t_{1} = (\Psi_{0} ,\emptyset ),} \hfill \\ {} \hfill & {t_{2} = (\Psi_{5} ,\emptyset ),} \hfill \\ {} \hfill & {t_{3} = (\Psi_{4} ,\emptyset ),} \hfill \\ {} \hfill & {t_{4} = \left\{ {(\Psi_{(3)} ,90),(\Psi_{(4)} ,\emptyset )} \right\}} \hfill \\ {} \hfill & {t_{5} = \left\{ {(\Psi_{(5)} ,\emptyset ),(\Psi_{(12)} ,0.3)} \right\}} \hfill \\ {} \hfill & {t_{6} = (\Psi_{11} ,0.2),} \hfill \\ \end{array}$$

Fig. 6

Six-image (2, 2)-RG scheme. a ${\mathcal{H}}_{1}$, b ${\mathcal{H}}_{2}$, c–h $\oplus$-stacks. i–n $\oplus^{CT}$-stacks

Table 6 Relative contrasts in binary (2, 2) 6-image RG

As expected, contrasts for $\Psi_{11}$ and $\Psi_{12}$ are lower due to clipping, but all six images are visible, even with OR-stacking.

In Fig. 7, using images C1 to C3, three images are encoded into two shares by lifting sides of ${\mathcal{H}}_{1}$ relative to ${\mathcal{H}}_{2}$. Transformations, results and contrasts follow. The scheme evolved within 30,000 iterations. Note that weights are used to give emphasis to the additional images (Table 7).

$$\begin{array}{*{20}l} {} \hfill & {t_{1} = (\Psi_{0} ,\emptyset ),} \hfill \\ {} \hfill & {t_{2} = \left\{ {(\Psi_{10} ,0.1),(\Psi_{8} ,0.04),(\Psi_{9} ,0.03)} \right\}} \hfill \\ {} \hfill & {t_{3} = (\Psi_{7} ,0.3),} \hfill \\ {} \hfill & {W[1,1] = 0.7,W[i,j] = 1,i,j > 1} \hfill \\ \end{array}$$

Fig. 7

RG scheme with projecting (i.e. lifting sides): a ${\mathcal{H}}_{1}$. b ${\mathcal{H}}_{2}$. c–e OR-stacks under $t_{1} ,t_{2} ,t_{3}$, respectively. f–h XOR-stacks. i–k Cleaned and thresholded XOR-stacks

Table 7 Relative contrasts resulting in 3-image projection (2, 2)-RG

As the algorithm optimises for OR-stacking, the weighting indeed produces higher contrasts in the projected stacks, but their contrasts are interestingly lower under other stacking operations. Experiments indeed indicate that this type of transformation degrades contrasts and it is beneficial to add a weighting in favour of it.

The example shares and stacks in Fig. 8 show 10 images from image set 2 encoded into two shares, using a range of transformations including distance and projection. For brevity, only XOR-stacks are shown, but mean contrasts for all operations are given in Table 8.

$$\begin{array}{*{20}l} {} \hfill & {t_{1} = (\Psi_{0} ,\emptyset ),} \hfill \\ {} \hfill & {t_{2} = (\Psi_{3} ,90),} \hfill \\ {} \hfill & {t_{3} = (\Psi_{3} ,180),} \hfill \\ {} \hfill & {t_{4} = (\Psi_{3} ,270),} \hfill \\ {} \hfill & {t_{5} = (\Psi_{4} ,\emptyset ),} \hfill \\ {} \hfill & {t_{6} = (\Psi_{5} ,\emptyset ),} \hfill \\ {} \hfill & {t_{7} = (\Psi_{11} ,0.1),} \hfill \\ {} \hfill & {t_{8} = (\Psi_{12} , - 0.1),} \hfill \\ {} \hfill & {t_{9} = (\Psi_{6} ,0.8),} \hfill \\ {} \hfill & {t_{10} = (\Psi_{10} ,0.2),} \hfill \\ \end{array}$$

Fig. 8

XOR-stacks of a 10-image RG scheme: a ${\mathcal{H}}_{1}$. b ${\mathcal{H}}_{2}$. c–l XOR-stacks under $t_{1} ,...,t_{10}$

Table 8 Mean transmission rates and relative contrasts in a 10-image (2, 2)-RG

All images are visible using all operations, albeit with reduced contrast, although it should be noted that this image set is very simplistic. To encode more complex images, it would be necessary to increase share dimensions to accommodate the extra information.

4.3 Security Analysis with JND Theory

In this section the security of individual shares and subsets forming $\Gamma_{forb}$ are analysed but the analysis does not apply to the reconstructions, noise-reduced or otherwise as only information in $\Gamma_{forb}$ must remained hidden. To perform this analysis, Just-Noticeable Difference Theory is used, which is a psychophysical theory using Weber's Constant to calculate the limen when tiny changes are made to a stimulus. This was proven to be a sound metric to measure visibility of VSS reconstructions by [21], which gives a Limits of Human Vision formula (LHV-VSS) based on stacked share transmission rates. They proved that even for non-zero $\alpha$, the secret is not leaked. Strictly speaking, they used VC, but the VSS method is immaterial. The following algorithm is adapted from their method, returning a Boolean determining whether ${\mathcal{S}}_{j}$ is visible in ${\mathcal{H}}_{i} ,i = 1,...,n$, as opposed to forbidden stack, as this paper focusses on graph access structures only. It takes as input the respective secret image ${\mathcal{S}}_{j}$, the share to be tested and viewing distance $\Delta$, which is a multiple of image height. It returns v, which equals true if the share leaks the secret.

Algorithm 4: Visibility of the Secret Based on JND Theory

$T_{0}$ and $\gamma$ can be seen as constants, but as shown in Tsai and Chen [21], the values here are only valid if $\Delta$ is greater than six times image height. G is not easily calculable, and it was recommended to simply make this a constant $G = 255$.

All images have original height 200 pixels and parameters $G_{0} ,G_{1}$ respectively equal 255 multiplied by white and black transmission rates. To demonstrate invisibility of the secrets in the forbidden subsets (including individual shares), JND theory is applied to the forbidden subset with the highest reported contrast. This was $\alpha = 0.023$ in Table 4. Based on a distance of 6.1:

• (1) $h = 200$

• (2) $G_{0} = 255*0.938 \approx 239.2$

• (3) $G_{1} = 255*0.915 \approx 233.3$

• (4) $d > 6\therefore T_{0} = 17,\gamma = \frac{3}{128}$

• (5) $G = 255 > 127\therefore LHV = \gamma (G - 127) + 3 = 6$

• (6) $V = G_{1} + LHV = 239.3$

• (7) $233 < V \not \le 239\therefore v = false$

The secret is therefore invisible in this forbidden stack, but it would be interesting to also verify adherence to the contrast constraint. For this, it is observed that the lowest contrast for a qualified subset is 0.044 in Table 5. Therefore, it holds:

• (1) $h = 200$

• (2) $G_{0} = 255*0.248 \approx 63.2$

• (3) $G_{1} = 255*0.204 \approx 52.0$

• (4) $d > 6\therefore T_{0} = 17,\gamma = \frac{3}{128}$

• (5) $G = 255 > 127\therefore LHV = \gamma (G - 127) + 3 = 6$

• (6) $V = G_{1} + LHV = 58.0$

• (7) $62.2 < V \le 63.2\therefore v = true$

JND therefore demonstrates security and contrast for shares and stacks presented here, as those with lower contrast than the worst case leak less of the secret by definition. Similarly, those with higher contrast than the best case must display a higher quality ${\mathcal{S}}\prime$.

For brevity, security for all possible results is not analysed here, but as discussed in Sect. 3, a stopping criterion of the SA is that the candidate solution contains a scheme with sufficiently small $\alpha$ for forbidden subsets to fall below (in most cases, far below) JND threshold.

5 Discussion

A comparative analysis with VSS research is given in Table 9. The VS Type is either Random Grids (RG) or Visual Cryptography (VC). A scheme is k-consistent if the relative contrasts in reconstructions are similar in value. Furthermore, VC has a rulebook, normally having two basis matrices used to respectively encode white and black pixels. These result in pixel expansion.

Table 9 Comparative analysis between the present work and other VSS research

ARG is capable of general graph access structures, i.e. where the minimum number of shares in any qualified subset is 2. Experiments in generating access structured with minimum $\left| {\Gamma_{qual} } \right| > = 3$ resulted in leaking of the secret image in the shares, due to the need to optimise all 2-share stacks for dissimilarity to the secret image(s). This merits further work. However, the majority of work in the field has focused on graph access structures.

ARG gives far more flexibility in terms of how multiple secrets are hidden in one scheme, but metaheuristics take more time to execute than analytical methods. Given that a candidate solution here is very large (collectively containing every pixel value in every share in the scheme), running the algorithm for each 50 iterations took approximately one second on a PC. For example, the scheme shown in Fig. 5 took almost 20 min to generate.

From the point of view of efficiency, all the prior studies given in Table 9 are highly efficient, taking just a few seconds to generate shares. A major limitation of the work in this study is the time taken to generate shares. Depending on the scheme complexity, this took between 5 and twenty minutes for the schemes presented in this paper. However, no previous study has demonstrated such a robust and flexible scheme in terms of multiple images with multiple and varied transformations. For share reconstruction, efficiency is not a problem for our method, as it only involves physical or computational stacking of shares, as in all prior studies.

6 Conclusion

This paper has introduced a method for RG schemes with flexible share stacking ability, hiding multiple secret images, therefore having high information rates. ARG produces generally good quality consistent shares by evolving them using SA that selects candidates in favour of higher relative contrasts and dissimilarity of shares to the secret image(s) and forbidden subsets.

The objective function optimises for schemes revealing additional secret images upon transformation of the first share in each qualified subset relative to the others, in any threshold or general graph access structure, enabling multi-image capability beyond that shown in prior works.

Security of ARG has been demonstrated using JND theory, which was shown to be applicable to VSS by Chen & Tsai [6], as it measures the theoretical limits of visibility. Given the stochastic nature of SA, information-theoretic security cannot be proven in a similar guise to prior work, but contrasts of forbidden stacks (and shares) are negligible and in most cases fall far below JND limits [28,29,30,31].

Further work is needed for hypergraph access structures through further metaheuristic experimentation. However, more interesting would be explore how to accomplish arbitrary multi-image hiding without these approaches at all, due to the time taken to generate a set of shares. Moreover, the integration of this approach with other technologies should be investigated in order to develop human centric solutions [32,33,34,35].

To conclude, the work presented in this paper has extended the capabilities of random grids for GGAS and multi-secrets beyond those previously achieved, enabling an arbitrary number of secrets to be encoded into one scheme in multiple arbitrary ways. The VSS Extractor algorithm has also been formulated to computationally extract the signal from extreme noisy reconstructions, further increasing information rate.