Topologically optimised facade brackets: an embodied carbon, structural and residual stress analysis

Abstract

The research investigates the topological optimisation of the metal brackets that connect curtain wall panelling to the floor slabs of a building. As is typically the case with standard building components, the brackets are overdesigned with higher load margins than real applied loads. Optimising them results in reduced mass and a more evenly spread stress distribution. Correspondingly, the question that the project asks is whether the optimised designs have a comparable structural performance to the standard bracketry used in construction, and a lower embodied carbon. To answer this, several optimisations of a standard facade bracket are performed, resulting in a total of six converged design options, with three of them progressed for fabrication. The manufactured designs are then horizontal and vertical load and residual stress tested to assess their performance, and an embodied carbon analysis is performed to calculate the corresponding emissions for raw material extraction, processing, and component fabrication. The results indicate the presence of compressive yield magnitude residual stresses, and that structural performance is comparable to a standard bracket, but embodied carbon is in most cases higher. The paper concludes with a discussion of the findings, and possible next steps in the optimisation, structural testing, and embodied carbon analysis workflow.

1 Introduction

The aim of the research discussed in this paper is to investigate the impact of topological optimisation (TO) on the structural performance and embodied carbon of building componentry. TO concerns the manipulation of an object’s geometry to fulfil a given task; for example, to carry a load with a minimum amount of material. When it comes to fabrication, recent advancements in additive manufacturing (AM) have enabled the realisation of full-scale topologically optimised building components, and therefore there is a growing body of research on this method in architecture. Literature review has shown that relevant optimisation and fabrication work focuses primarily on building beams (Vantyghem et al., 2020; Wethyavivorn et al., 2022; Ye et al., 2021), floor slabs (López et al., 2014; Ma, 2022), structural nodes (Lange et al., 2020; Ren & Galjaard, 2015), formwork (Aghaei Meibodi et al., 2017; Huijben, 2016; Jipa et al., 2016; Søndergaard & Dombernowsky, 2017), and lattice structures (Bao et al., 2022a, b).

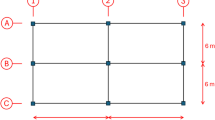
Adding to this research, the TO project herein concerns a component type that has not been explored previously, namely facade bracketry. These types of brackets are typically made of steel (Q235 in this study), and they are fixed to the concrete slabs of a building on one end, while supporting curtain wall panelling on their other end (Fig. 1). They are often overdesigned with higher load margins than real applied loads. More specifically, when stress checked, a solid, non-optimised bracket plate undergoes a shear stress of 4 MPa, and a bending stress of 231 MPa, which is less than steel’s material strength of 235 MPa. This demonstrates that the plate is utilised up to 98% but only at the governing region, whereas utilisation is low in most other locations. The amount of material in the bracket can therefore be reduced by achieving a more fully stressed design, while maintaining the required structural performance.

Fig. 1

Rendering showing the connection of the curtain wall panels to the concrete floor slab. The facade brackets are highlighted with a red outline

When it comes to manufacturing, AM invariably introduces high magnitude residual stresses into metallic components made for engineering applications (Attallah et al., 2016; Bastola et al., 2023), as well as creating material with (undesirable) strong texture (Attard et al., 2020; Forsey et al., 2018) and containing microscopic defects including porosity. The performance of AM structural components, such as the TO brackets in this paper, can be compromised by tensile residual stresses that promote stress corrosion cracking, fatigue crack growth from defects under cyclic loading and reduced load margins against fracture (Bastola et al., 2023; Withers, 2007). For framework type structures there is an additional potential risk of buckling that can be exacerbated by compressive residual stresses present. Therefore, for structural integrity purposes it is important to know the nature, i.e. tensile or compressive, and the distribution of residual stresses in AM components and to take account of them in design (AMS B Finishes Processes and Fluids Committee, 2023; BSI Standards Limited, 2019).

Another relatively unexplored area is the impact that TO has on reducing the embodied carbon of building components. Two of the main parameters that affect carbon footprint are the method of fabrication and mass of a part. Regarding fabrication, research like the detailed lifecycle analysis by Hussain Shah et al. (2023) investigate the climate change impact of wire arc additive manufacturing (WAAM) a TO steel beam, but there is no such analysis of binder jetting (or powder bed manufacturing) smaller, full-sized TO building components.

Effectively, rather than concentrating on the optimisation process itself, this paper focuses on a comparative analysis of the structural performance and embodied carbon of TO facade brackets versus the standard plate that is used in construction. Additionally, it presents a characterisation of residual stresses in one of the fabricated brackets. Section 2 discusses different generative design options with various constraints, as well as corresponding fabrication methods. Section 3 focuses on comparative structural analyses of the optimised designs, Sect. 4 discusses a residual stress characterisation of a TO bracket, and Sect. 5 presents an embodied carbon analysis of material production and TO component fabrication, comparing the resulting CO₂ emissions figures to the one of the original bracketry. The concluding section summarises the findings and discusses possible next steps.

2 Structural design and fabrication

2.1 Optimisation

A facade bracket system is typically designed to carry the vertical (dead) load of a curtain wall panel and corresponding external horizontal loads (wind suction). In this case study, only the main steel plate of the system, with dimensions of 615 mm × 240 mm × 16 mm (l × w × t), is examined. When it comes to structural optimisation in architectural applications, generative design (GD) and TO are typical methods of finding designs with improved properties, such as stiffness or minimal mass, within boundary condition restrictions.

TO optimises material distribution in a preset design space. Material is removed or rearranged during the optimisation loops, and the resulting structure is utilised as fully as possible under a given load (Wang et al., 2003; Yan X. et al., 2023a, b). TO is used by commercial software such as Altair OptiStruct and the Grasshopper plugin TopOpt, which are based on Bendsøe and Sigmund's SIMP approach (Solid Isotropic Material with Penalization) (Bendsøe, 1989; Sigmund, 2001). In SIMP, each finite element is assigned a relative density as a design variable. The element stiffnesses are then adjusted via this variable, and there is an exponential relationship between element stiffness and density. The objective function is to minimise the total strain energy of the component, which corresponds to a minimisation of mean compliance, i.e., a maximization of stiffness. An approximation method is used as the optimisation algorithm. The SIMP approach leads to a penalty of mean densities in the design space and thus to a 0/1 material distribution. As a result, TO converges to a component that is optimised in terms of its stiffness.

GD methods explore multiple possible designs for a given design space and different constraints like component manufacturing methods. Shea et al (2005) define GD methods as “systems [that] are aimed at creating new design processes that produce spatially novel yet efficient and buildable designs through exploitation of current computing and manufacturing capabilities”. In GD, each design is evaluated against performance parameters such as stiffness, mass, and cost. Similarly to nature’s evolutionary approach, permutations of preformatted design solutions are generated and recursively revaluated (Xie & Steven, 1993; Huang et al., 2008) and low structural performance or restriction violating designs are discharged. This can be seen as an evolutionary process that requires high design divergence to explore as many solutions as possible and find the fittest design.

Here, to optimise the flat plate, the commercial software Autodesk Fusion 360 was used. Autodesk does not specify the algorithms behind GD in Fusion 360 (Savage, R. 2018) or allow their customisation, but it has recently incorporated new experimental solvers with features like symmetry enforcement in outcomes, insertion of voids, and buckling constraints (Motawa, K. 2020).

In effect, the objective was to achieve a minimal mass design with a target overall safety factor of 2 as a restriction. The overall safety factor of 2 was determined in a static stress study where a safety factor of 1 would lead to yielding. A unity load of F_V = 1 kN in each of the two vertical loading points and a horizontal load of F_H = 1.654 kN in each of the two horizontal loading points was set. The factor F_H / F_V = 1.65 is equivalent to the proportion of the design loads F_{ed, V} = 11.31 kN (design vertical force) and F_{ed, HS} = 18.71 kN (design horizontal force suction), which were the loads in the structural design report of the reference solid plates. The four vertical anchor bolts formed fixed supports in the translational degrees of freedom Fig. 2.

Fig. 2

Setup of the structural optimization in fusion: a starting geometry of the plate b preserved geometry of the supports in green and loads in red c obstacle geometry in red

After supports and loads were set, several optimisations with partial and full Z axis constraints were performed, resulting in a total of six converged design options. The designs were then assessed against the performance factors shown in the generative design results viewer that included weight, displacement, and possible manufacturing methods Fig. 3.

Fig. 3

Comparison of all converged design options. Safety factors are expressed as the ratio of the maximum strength of the material to the actual stress in the part. Minimum Factor of Safety = Yield Strength / von Mises equivalent stress

When it came to stress distribution, a high percentage of the parts appeared to be uniformly stressed due to the optimisation. However, this was only a first indication and only detailed FEM analyses will allow the exact assessment of stresses and strains Fig. 4.

Fig. 4

Stress based utilisation of outcome 5 (TO1), outcome 6 (TO2) and outcome 4 (TO3)

Three options, outcome 4 (TO3), a flat design, which could potentially be three-axis milled, outcome 5 (TO1), which had the highest stiffness based on the factor (minimum displacement × mass), and outcome 6 (TO2) were selected for postprocessing, production and testing. These were also the options with the highest recommendation percentage. Lastly, despite a symmetry in load assignment and modelling, some of the designs (like TO2) exhibited asymmetries in their geometry and the 3D models were therefore manually mirrored Fig. 5.

Fig. 5

Selected design variants for post processing, production, and testing. The top row consists of the optimisation results, and the bottom row of the mirrored designs fixed to the concrete floor slab, with connections to the curtain wall panel at the bottom left of each render. The side that was selected for mirroring in each outcome was the one with the lower mass and effectively lower embodied carbon

2.2 Fabrication

Due to the geometric characteristics of each design, CNC milling and 3D printing were deemed the most suitable fabrication methods. Metal casting was also considered, but it was later abandoned as an option. This was because of its prohibitive cost and the negative environmental impact of fabricating one-off casting moulds that would eventually have to be discarded. To be able to load test the brackets a scaling of 1:2 was done in all dimensions for fabrication, leading to the dimensions and test loads in Table 1.

Table 1 Scaling of components for production and testing

CNC milling was used for the planar design (TO3), and 3D printing for the non-planar ones (TO1 and TO2). Due to the unavailability in the UK of Q235 steel (which is a grade typically used in China) and its European equivalent S235, the closest grade, EN3B 080A15, was used for the milled part (TO3). Regarding 3D printing, steel bronze (420SS / BR) is a common and relatively inexpensive metal that allows the materialisation of complex geometric features and therefore TO2 was fabricated in it. This is also as Q235 cannot be used in 3D printing. Additionally, TO3 was also fabricated in steel bronze, to compare the structural performance of the bracket in that material to the same one CNC milled in EN3B 080A15 steel. TO1 had a lower mass than TO2, consisting of longer and thinner elements, and it was therefore not possible to realise it in 420SS / BR. Following post thickening of these elements to a minimum of 4 mm, TO2 was 3D printed in stainless steel (316L).

Lastly, two copies of each bracket design were fabricated, one for horizontal and the other for vertical load testing (Fig. 6). Additionally, solid plate equivalents in all these materials (S235,¹ 420SS / BR and 316L) were also laser cut or 3D printed, to perform a like-for-like structural comparison of the optimised to the solid bracketry.

Fig. 6

All the specimens fabricated for the research project: the four bracket copies (TO3) on the left were manufactured in EN3B 080A15, the four bracket copies (TO1) on the right in grey were 3D printed in stainless steel, the two brackets (TO3) on the left in bronze colour were 3D printed in 420SS/BR, and the two brackets (TO2) on the right in bronze colour were also 3D printed in 420SS/BR

3 Structural testing

The question that this part of the research aimed to answer was whether, compared to the solid bracket, the TO brackets had an adequate structural performance Fig. 7.

Fig. 7

Two of the optimised brackets (TO1 on the left in stainless steel and TO2 on the right in 420SS/BR) next to the reference solid plates in the same material

To investigate this, a series of structural tests were performed on a Zwick Universal testing machine at the MPA Schleswig Holstein facilities of TH Lübeck in Germany. As mentioned, each component was manufactured twice, one for loading up to F_V,ultimate and one for loading up to F_HS,ultimate. The testing was done in the following order: each component was mounted in the configuration for vertical loading (see Figs. 8a and 9 – left) and loaded displacement controlled with 0.02 mm/s up to 4.3 kN machine load or up to 5 mm machine way. After reaching one of both values the component was unloaded. The next step consisted of mounting the component in the horizontal configuration (see Figs. 8b and 9 – right) and loading with 0.005 mm/s up to a machine load of 7.1 kN. After reaching 150% of the vertical and horizontal design loads, one component at a time was tested until failure, in the vertical and the horizontal configuration. This resulted in the following four test series (P1-4):

• P1: vertical loading (component bending) of all 14 components, with 0.02 mm/s up to 4.3 kN or max. 5 mm deflection.

• P2: horizontal loading (component tension) of all 14 components with 0.005 mm/s up to 7.1 kN.

• P3: horizontal loading (component tension) of 7 components up to failure.

• P4: vertical loading (component bending) of 7 components up to failure.

The name of each test in the graphs consists of the test series P1 – P4 and the component number TO1.1 – F7.2, e.g., “P2_TO3.4”. “TO” stands for topologically optimised, and “F” for full (plate) Fig. 10.

Fig. 8

Drawing of the setups including the adaptation parts for structural load testing: a) design of the vertical loading configuration b) design of the horizontal loading configuration. The loading locations are shown in red

Fig. 9

Photos of the TO3 vertical (left) and horizontal load testing (right)

Fig. 10

Render and table of all the pairs of optimised and standard brackets to be structurally load tested. The lines at the top show the materially equivalent optimised and non-optimised brackets

Figure 11 shows the load displacement curve of the vertical configuration for the gravity loading of the facade, as a pretest of two selected components to verify the assumptions and test setup. Deflection is measured as the machine way and at the top of the load transferring beam with two inductive gauges (marked as spider in Fig. 11). Further on it will only be reported the machine way, but inductive measurements were also conducted for the tests. Figure 11 shows that both measurements were almost identical. While component TO3.1 reaches the predefined test loading of 4.3 kN staying in the linear elastic range, component TO1.1 shows plastic deformations in the load deflection curve, as well as visible plastic deformations after the testing. The tip deflection of TO1.1 with 4.28 mm compared to TO3.1 with 1.88 mm, is 2.3 times higher.

Fig. 11

The results of the component testing in the vertical load configuration

Figure 12 shows the test results of test series P1, with a maximum load of approximately 1.5 times the design load F_ed,V from Table 1. All components reach this load, which can be seen as the minimum requirement with some load reserve since the material safety factor of steel in bending is γμo = 1.0. From these tests, it could be concluded that the 3D printed components TO1 and TO2 together with the 3D printed steel bronze component TO4 are significantly softer than the full plates. The CNC milled EN3B 080A15 steel component TO3 shows the second highest stiffness, while the full steel plates F5 and F7 show the highest stiffness, as expected. Components TO1, TO2 and TO4 show a degrading stiffness with starting plastic deformations, while TO3, F5, F6 and F7 stay linear elastic. All components stay linear elastic up to the design load F_ed,V. Although these tests were very informative, to have a more meaningful comparison, a stiffness to weight factor had to be calculated. This is presented below in Table 2.

Table 2 All test components, materials, and results

Fig. 12

The results of series P1 showing all 14 (2 × 7) tests

Figure 13 shows the test results of the horizontal wind suction loading. The wind suction is inducing mainly a tensile load into the component. All tested components are behaving linear elastic under the loading, reaching the preset maximum load of 7.1 kN with a relatively small displacement up to 1.2 mm. After unloading, no plastic deformations were visible. The slight nonlinearity of the load displacement curves results from slipping of the load transferring plates in the test. This happened significantly in tests P2_TO2.1 and P2_TO1.1, which are removed in Fig. 14 to be able to see the differences between the components. Again, the 3D printed parts TO1 and TO2 have the softest response. Interestingly, the 420SS / BR plate P2_F6 shows the highest stiffness of all components in the tensile test but has the most reduced bending stiffness of all full plates in test P1_F6.

Fig. 13

The results of series P2 showing all 14 (2 × 7) tests

Fig. 14

The results of series P2 showing all 14 (2 × 7) tests, without tests P2_TO1.1 and P2_TO2.1 where the load transferring clamping slipped

Figure 15 shows the ultimate tensile capacity of all components. Even after readjusting the clamping for the load application, slipping at higher loads could not be fully prevented. Pictures of the failure modes of each component can be found in the appendix. Component TO1.2, as the lightest 3D printed component, failed at a load of 22.9 kN, which is 4.9 times the design load F_ed,HS. Component TO2.2 showed ductile behaviour with high deformation capacity and a failure load of 39.64 kN (7.2 × F_ed,HS). TO1.2 and TO2.2 yielded at the position of the smallest cross section and subsequent fracture occurred at that point. CNC milled TO3.2 and 3D printed TO4.2 performed well in this test, reaching 47.2 kN and 40.5 kN respectively. Slipping at the clamping occurred in both components and therefore they could not be loaded up to full capacity. The plates (F5.2, F6.2 and F7.2) could not be loaded up to their full capacity, which would be 225.6 kN for a plate in Q235. In the appendix, the slipping at the clamping locations is clearly visible from the scratches.

Fig. 15

The results of series P3 showing the 7 tests loaded until tensile failure or anchorage slipping

Figure 16 shows the ultimate bending capacity of all components. Pictures of the failure mode of each component can be found in the appendix. They all formed plastic hinges under bending, at the position of the smallest cross-sectional area by bending moment ratio at that position. For the plates with a constant cross section across the full length of the component, this position is at the highest bending moment i.e., the edge of the concrete slab that the plate sits on (e.g., P4_F7.1). Due to the variation of the cross section of the optimized components this position can be shifted closer to the load application point. Component TO1.1 as the lightest 3D printed component failed at a load of 5.2 kN, which is 1.8 times the design load F_ed,V. Component TO2.1 showed a hardening behaviour with plastic capacity and a failure load of 6.9 kN (2.4 × F_ed,HS). Also, components TO3.2 and TO4.2 again performed well in this test, reaching 8.8 kN and 7.2 kN respectively. The plates F5.2, F6.2 and F7.2 were also loaded up to their full capacity, which was 10.6, 13.1 and 13.4 kN respectively.

Fig. 16

The results of series P4 showing the 7 tests loaded until bending failure

Table 2 summarises all test results. Two performance factors, stiffness to weight for the design load tests P1 and P2, and ultimate load to weight for the tests P3 and P4 were calculated. The stiffness to weight factor is calculated as = (F_test/d_max,test)/Weight [(N/mm)/g]. The ultimate load to weight factor is calculated as = F_ultimate/Weight [N/g]. Irregular test results are shown in italics.

The lightest component TO1 shows a stw_b/t (stiffness to weight factor in bending/tension) of 2.66/12.1. For the corresponding stainless steel full plate component F5, the stw_b/t factors are 1.3/3.8, which is significantly smaller. Similar factors can be seen comparing TO2 stw_b/t 1.25/7.13 to F6 stw_b/t 0.91/5.36. TO1 and TO2 are both 3D printed components. Milled EN3B 080A15 component TO3, shows stw_b/t factors of 3.13/11.52 in comparison to S235 steel plate F7 stw_b/t 1.32/4.62. All three comparisons show significantly higher stiffness to weight factors in the optimised components, validating the assumption that TO can be used to design lightweight parts with improved stiffness.

Also, an ultimate load to weight factor was calculated to see the effect of the optimisation on the ultimate load bearing capacity, since the primary optimisation aim is maximising stiffness. The ultimate load to weight factors of the optimised parts ranged between 47.40 to 59.50. The ultimate load to weight factor for the standard plates ranged between 14.01 and 22.68. All comparisons showed an improved structural behaviour for the optimised components if the reduced weight is considered. All optimised components reached the predefined required 150% design load in the tests, making them structurally safe and compliant.

Effectively, the testing proved that TO can be used to design and build load bearing building components with savings of up to 79% of weight. Having said that, deviations from the predefined loads were not considered and standard components will offer more resilience for differing loads resulting from usage changes. However, in the selected facade brackets here, the considered load cases will most likely remain the governing load cases.

4 Residual stress analysis

Residual stresses in AM components can be characterised by using one or more measurement techniques (Schajer, 2013) including laboratory X-ray diffraction (XRD), neutron diffraction, synchrotron diffraction, incremental centre-hole drilling (ICHD), deep hole drilling, slitting and the Contour method. Here we present results of laboratory XRD measurements of residual stresses at the surface and immediate sub-surface of the TO1 bracket.

Residual stresses are difficult to measure in metallic AM components using laboratory XRD for several reasons: the surface finish of components is usually rough, the geometry often has a complex shape, the grains are sometimes large, the microstructure can be strongly textured, and secondary phases may be present. The surface roughness of the 316L stainless steel bracket was measured at 13 locations giving a mean Ra level of 4.9 ± 1.8 μm. Erroneous XRD residual stress measurements are not expected with this level of roughness (Li et al., 1995) because it is less than the penetration depth of X-rays (from a Mn K-α source) of around 10 μm in stainless steel. The complex geometry challenge of the bracket was readily overcome by precisely positioning a robotic X-Ray diffractometer using an Adaptive laser scanning system developed by Stress-Space Ltd (Stress-Space Ltd., 2024). The potential problem of sampling too few grains was addressed by using a 2 mm diameter sampling area and applying ± 3° oscillation during each measurement and the presence of texture was checked by monitoring the shape of the XRD ${sin}^{2} \psi$ correlations (as no microstructural information was available).

All residual stress measurements followed NPL Measurement Good Practice Guide No 52 (Fitzpatrick et al., 2005) and used laser guided robotic X-ray diffractometer equipment (X-Raybot manufactured by Mesures Rayons X). The XRD goniometer, mounted on a collaborative robot, was equipped with a pure Si solid state detector having an angular range of 20° to 35° and an interchangeable X-ray tube with air cooling. The goniometer was positioned using an Adaptive Laser System that first scanned the surface geometry of interest and then allowed rapid definition of sets of measurement points and vectors to tolerances better than 100 microns. Figure 17 shows a photograph of the region of the bracket measured and the corresponding laser surface scan image with illustrative measurement points (green globes) marked up. A 2 mm diameter collimator was used with a Mn K-α anode and Cr filter to detect the X-ray diffraction response from austenite {311} crystallographic planes. Measurements were made using 17—25 tilt (ψ) angles and an exposure of 30 s with ± 3° ψ-oscillation. Measured data were processed using StressDiff software supplied by the diffractometer manufacturer.

Fig. 17

Photograph and X-Raybot laser scan (2 mm green grid) of the bracket front surface showing the position and longitudinal direction where residual stresses were measured by XRD after locally electropolishing the surface to depths in the range 111 to 168 μm

Initially residual stresses were measured on the front surface of the as-received component (with no surface preparation applied) at several points in the longitudinal and transverse directions. All the front surface measurements indicated the presence of compressive residual stresses (-584 MPa ± 47 MPa) of magnitude consistent with the expected yield strength of high energy deposition SLM Type 316 stainless steel. Similar magnitude compressive stresses were measured on the back face. However, the uncertainties in the data fitting were large; typically, ± 31 MPa for the diffraction peak fits (see inset on Fig. 18) and ± 53 MPa for essentially linear ${sin}^{2} \psi$ fits.

Fig. 18

Residual stress depth-profile measurements at Point 3 (see Fig. 17) on the front surface with inset diffraction peak data for the surface point and a sub-surface point

Secondly, sub-surface residual stresses at location 3 (Fig. 17) were measured by incrementally removing thin surface layers of material by electropolishing (a stress-free process). XRD measurements were performed in the longitudinal and transverse directions after each excavation to a final depth of 168 μm. The XRD results are plotted in Fig. 18 and show a steep sub-surface gradient in residual stress, in both directions, varying from high level compression at the surface to substantial tension at depths greater than 60 μm. The diffraction peaks for the deep measurements were much sharper and well defined giving much lower peak fit errors than the surface measurements, see diffraction inset in Fig. 18.

Thirdly, XRD residual stress measurements were conducted at selected points on the front face (Fig. 17) after local electropolishing to depths greater than 100 μm. Good quality diffraction peaks were obtained at all points measured giving mean tensile residual stresses of 309 MPa ± 54 MPa in the longitudinal direction. Similar magnitude tensile residual stresses (345 MPa ± 74 MPa) were measured at equivalent electropolished depths from the back face. However, the ${sin}^{2} \psi$ correlations for some of these at depth measurements had an oscillatory nature which is indicative of preferred orientation (texture) being present in the substrate.

The XRD residual stress investigation has indicated the presence of compressive yield magnitude residual stresses on the front and back faces of the bracket that sharply increase with depth and reach a tensile plateau of about 50% of the material yield strength at 60 μm depth. Detailed microstructural investigation is desirable to reveal the origin of the surface compressive layer and to characterise texture in the substrate. It would also be worthwhile undertaking ICHD measurements (that are insensitive to microstructure) to depth-profile the residual stress field to 1 mm below the surface and confirm the XRD findings.

5 Embodied carbon analysis

The question that this part of the research aimed to answer was whether the embodied carbon of the TO brackets was lower than the one of the solid plate.

Although the brackets were fabricated in various steels for structural load testing, for the embodied carbon analysis, stainless steel was assumed for all optimised designs. This was to focus on a like-for-like comparison of the impact of different geometric characteristics and fabrication methods on embodied carbon emissions. The assessment was made for the original solid bracket plate and TO 1,2, and 3, as well as an alternative option for TO3. As the original bracket was made of plate steel, the first part of the assessment was on the CO₂ emissions of stainless steel (316L) plate production. Metal powder is used in binder jetting the optimised brackets; therefore, the second part of the assessment was on stainless steel (316L) powder production.

The assessments were performed by Tunley Engineering to the international standards BS EN ISO 14067:2018 Greenhouse Gases – Carbon footprint of products – requirements and guidelines for quantification, Part 6: Methodology for quantification of the CFP and partial CFP; following a manner consistent with International Standards on Life Cycle Analysis (LCA) (ISO 14040 and ISO 14044) and The Greenhouse Gas Protocol. Quantification of carbon dioxide equivalent emissions arising from production and transportation activities was completed in accordance with emission factors published by the relevant national government, for example DEFRA 2022. For the UK manufacturing facilities, the emission factors published by the UK government Department for Business, Energy and Industrial Strategy was applied.

The assessment was based on emission sources, firstly, for producing the material and secondly, for manufacturing. Material transportation activities were assumed to be insignificant and were not considered. Stainless steel (S316 LSI) was assumed to have the following composition of different elements by weight (%): Iron (Fe) = 64.810%, Carbon (C) = 0.020%, Manganese (Mn) = 1.700%, Silicon (Si) = 0.900%, Chromium (Cr) = 18.500%, Nickel (Ni) = 12.000%, and Molybdenum (Mo) = 2.700%. Effectively, the emissions for producing a kilogram of raw stainless steel were calculated to be 3.421 kgCO₂e/kg. This figure is higher than other types of steel like S235, and mild steel, due to the inclusion of metals such as nickel and chromium that are mined and processed using resource intensive methods.

In terms of manufacturing, a rolling mill method was assumed for the ‘global’ steel plate fabrication. The smaller, solid facade brackets are cut from this global steel plate. The embodied carbon emissions of the rolling mill process were calculated at 0.264 kgCO₂e/kg by Tunley Engineering (Fig. 19). Given its (half size) dimensions of 307 × 120 × 8 mm and 316L stainless steel’s density of 8,000 kg/m³, the weight of one plate came to 2.342 kg. The rolling mill CO₂ emissions figure corresponding to the mass of the solid bracket is therefore 8.63 kgCO₂e ([3.421 kgCO₂e/kg for raw stainless-steel production + 0.264 kgCO₂e/kg for rolling mill fabrication] × 2.342 kg of the solid bracket mass).

Fig. 19

Chart of the CO₂ emissions of material extraction and processing for steel plate and 3D printing powder production

The facade brackets are typically cut from the global plate using a method like waterjet cutting. It takes 6.8 min to fabricate one bracket using a 40HP Maxiem waterjet cutting machine, with max jet power at 34 HP (25 kW). Effectively, 0.113 h (6.8 min) × 25 kW = 2.825 kWh. For the calculation to be consistent with Tunley Engineering’s assessment, the DEFRA (UK’s Department for Environment Food and Rural Affairs) 2022 figure of 0.193 per kgCO₂e per kWh unit was used. 2.825 kWh would be equivalent to emissions of 0.545 kgCO₂e. Therefore, the total embodied carbon figure of the solid facade bracket at half size comes to 8.63 kgCO₂e + 0.545 (waterjet cutting) kgCO₂e ≈9.170 kgCO₂e.

The method for manufacturing TO3 was CNC milling. As mentioned, this is because the overall geometry is planar, except for the mid-relief top surface of the bracket, which can nevertheless be fabricated using a three-axis subtractive process. It takes 10 h to mill four of these brackets using a Haas TM3P machine, powered at 5.6 kW. Therefore 2.5 h (per part) × 5.6 kW = 14 kWh. According to DEFRA 2022 an energy use of 14 kWh equates to 2.7 kgCO₂e. Given the volume of the TO3 plate (0.0001 m³) and the density of 316L stainless steel at 8,000 kg/m³, its weight comes to 0.808 kg. This plate is CNC milled also from a larger solid plate, which again is firstly roll milled and then waterjet cut to size. Assuming that the plate to be CNC milled has the same bounding box dimensions as the solid facade bracket, the rolling mill emissions would be the same as above i.e., 8.63 kgCO₂e ([3.421 kgCO₂e/kg for raw stainless-steel production + 0.264 kgCO₂e/kg for rolling mill fabrication] × 2.342 kg). The cutting of the plate would also have the same emissions as above i.e., 0.545 kgCO₂e. Therefore, the total embodied carbon figure for TO3 comes to 8.63 kgCO₂e (raw steel production and rolling mill fabrication) + 0.545 kgCO₂e (waterjet cutting) + 2.7 kgCO₂e (CNC milling) ≈11.875 kgCO₂e. Effectively, although the mass of TO3 is almost three times less than the fully solid plate, due to all these manufacturing processes involved, its embodied carbon is approximately 1.3 times higher. Additionally, there is waste material due to the CNC milling process that needs to be recycled, which would add to the embodied carbon total.

An alternative to this, termed TO3_alt, would be to produce a straight cut in the shape of TO3, with the top part of the bracket being planar. Although the resulting bracket would have more material than TO3, the energy consumption and waste material associated with CNC milling would be avoided. The weight of the resulting plate would come to 1.0 kg (0.000129 m³ × 8,000 kg/m³) and it would take 12.1 min to cut one using the same 40HP Maxiem waterjet cutting machine. Therefore, 0.2 h (12.1 min) × 25 kW = 5 kWh. According to DEFRA 2022, 5 kWh equate to 0.965 kgCO₂e. As above, the plate would be cut from a larger roll milled plate, but here the embodied carbon would be less because the weight of this plate is lower: (3.421 kgCO₂e/kg for raw stainless-steel production + 0.264 kgCO₂e/kg for rolling mill fabrication) × 1.0 kg = 3.685 kgCO₂e. Therefore, the total embodied carbon figure for TO3_alt would come to 3.685 kgCO₂e + 0.965 (waterjet cutting) kgCO₂e = 4.65 kgCO₂e. This is approximately 4.5 kgCO₂e less than the solid bracket. Due to the non-rectangular shape of TO3_alt, however, and although it would be possible to optimise the nesting of these brackets within the global flat plate, there would be material left over at the end of the fabrication process. These offcuts would have to be recycled or cut into smaller parts to be used for a different purpose. Interestingly here, this bracket has a lower embodied carbon weight than the original one, but its non-orthogonal shape would potentially result in unutilised material and therefore a corresponding increase in its CO₂ footprint.

Regarding the 3D printed brackets, the stainless steel (316L) powder for additive manufacturing is produced using a gas atomisation method. It was assumed that this process is carried out using electricity, and the increase in temperature was 130 °C. This is because melting of metal components takes place at 150 °C and 20 °C is taken as the starting temperature. Effectively, the CO₂ emissions of gas atomisation were calculated at 0.0035 kgCO₂e/kg by Tunley Engineering. Regarding 3D printing, as mentioned, the method used for fabricating some of the brackets was binder jetting. This process consists of several steps that include binder deposition on a powder bed, binder drying, curing, de-binding, and sintering. Performing a comprehensive lifecycle assessment of binder jetting would require an entire article focussing solely on it. Therefore, here, the focus is limited to the total amount of electrical energy used in the process.

Going back to TO3, an alternative fabrication method for avoiding the waste material of CNC milling would be to 3D print the bracket. Having consulted with ExOne, a 3D printer manufacturing company, the total energy cost for binder jetting one TO3 bracket would come to $65.92. According to the company’s costing estimator, the energy cost per kWh ($/kWh) was $0.36. So, the total energy for producing one bracket would be $65.92 / $0.36 = 183 kWh, which comes to ≈35.3 kgCO₂e (183 kWh × 0.193 kgCO₂e per kWh). The embodied carbon of the material itself would come to ≈2.76 kgCO₂e (3.421 kgCO₂e/kg × 0.808 kg), while bearing in mind the low weight of the bracket and the minute CO₂ output of the process, the gas atomisation emissions were not included in the calculation. Effectively, the total for 3D printing TO3 came to ≈38 kgCO₂e. With the same energy cost for TO1, the total energy cost for producing a single bracket would come to $26.44. Effectively, the carbon emissions would be $26.44 / $0.36 ≈ 73 kWh, which is 14.17 kgCO₂e. TO1 weighs 0.48 kg (0.00006 m³ × 8,000 kg/m³) and the material production emissions would be ≈1.64 kgCO₂e (3.421 kgCO₂e/kg × 0.48 kg). Omitting the negligible gas atomisation emissions, the total for TO1 was 15.81 kgCO₂e. Lastly, for TO2, the total energy cost for one bracket would be $83.50, which is approximately 44.76 kgCO₂e. Its weight was 0.72 kg (0.00009 m³ × 8,000 kg/m³) and the material production emissions ≈2.46 kgCO₂e (3.421 kgCO₂e/kg × 0.72 kg). Effectively, the total for TO2 was ≈47.2 kgCO₂e.

The main observation here is that although TO3 and TO2 had a very similar mass, the emissions for producing the latter were almost 9 kgCO₂e higher than the former. Additionally, when comparing TO1 and TO2, the latter was 1.6 times heavier than the former, but the embodied carbon of TO2 was 3 times higher. The reason for this is the higher printing time of TO2, which was approximately 2 h, versus the one of TO1, which was approximately 1 h. As shown, however, the emissions from electricity use for 3D printing (14.17 and 44.76 kgCO₂e respectively for TO1 and TO2) were not proportional to printing times, with the printing time ratio being 1:2, and the emissions ratio being ≈1:3. Effectively, the main question is why there is this difference in printing times and more importantly in electricity consumption.

The two brackets are similar in terms of formal complexity, but one difference is that TO2 consists of larger sections of material concentrated in parts of the bracket, whereas TO1 mainly consists of thin linear elements (Fig. 20). Therefore, there is more energy spent to binder jet those larger regions. An additional reason could be the difference in printing orientation of the two brackets. The TO1 3D printing analysis figures were derived from having four copies in one job, placed horizontally across the 3D printing bounding box. The TO2 figures were from arranging twenty-six copies vertically. It could be that this change in orientation resulted in the above-mentioned differences, but this would need to be verified with the manufacturer. If this was to be confirmed, an optimisation in the arrangement of these elements within the printing box to achieve a minimisation of the input energy would be needed.

Fig. 20

Close up photographs of the 3D printed TO1 bracket on the left and TO2 on the right

Table 3 shows all bracket designs, and the weight, manufacturing method, and carbon emissions for material production and bracket fabrication. Regarding the latter, the generated emissions are directly related to electricity consumption and a fixed figure of 0.193 per kgCO₂e per kWh unit was used for the conversion. But if one were to look at this more closely, it would become evident that this number could fluctuate depending on the electricity source make-up at any given time. In the UK for instance, in August 2023, this figure was 0.161 per kgCO₂e per kWh unit, and in October 2023, it was 0.138 kgCO₂/kWh, with 54% of the electricity coming from renewable sources and 27% from gas. So, depending on the time and date of 3D printing, the emissions figure would be different.

Table 3 Table showing all the TO designs, manufacturing methods and corresponding CO₂ emissions breakdowns

Looking further ahead, the UK steel sector’s decarbonisation “roadmap strategy uses six “levers” to show exactly where carbon savings can be made” (Steel for Life, 2023). One of these levers is the decarbonisation of the national electricity grid. This will result in electricity consumption emissions reducing steadily towards the net zero-year of 2050. Effectively, there will be progressively less CO₂ generated for 3D printing componentry like TO 1, 2, and 3, and most emissions will result from raw steel production, which typically takes place in a blast furnace and basic oxygen furnace (BF-BOF). In this case, all the optimised designs will have a lower embodied carbon than the original, as embodied carbon will become directly associated to mass.

The main alternative steel production method is the electric arc furnace (EAF) process. Unlike BF-FOF that produces new steel from raw ore, EAF is a 100% scrap-based process that depends on the availability of scrap material to produce steel. Effectively then, if production ends up taking place with recycled material, using zero emissions electricity, the mass of the components will also be disassociated from embodied carbon. But from a circularity point of view, optimised and efficiently designed componentry will capture less steel in the structure of a building, allowing more material to enter supply and eventually be used as scrap, with this “increased availability of scrap driving new steelmaking capacity towards EAF” (Steel for Life, 2023). So, the benefits of mass reduction due to TO will remain important even in the anticipated no-emissions electricity future.

6 Findings and conclusion

In this paper, we investigated the impact of TO on the embodied carbon and structural behaviour of a facade bracket component. The use of TO and generative design is becoming widespread (Xie, 2022) in design research and architecture, but the benefits of these techniques have not been studied extensively. Additionally, although TO results in mass and as a result embodied carbon reduction in building components, the use of energy intensive AM techniques to realise TO components tends to cancel this out. Our analysis has shown that this is marginally the case in the TO components with simpler forms (TO4), and more so in components with more complex geometries (TO1 and TO2). Having said that, the decarbonisation of the electricity grid promises to tip this balance in favour of AM TO components, even when these have complex forms, but a more comprehensive and detailed carbon footprint analysis of binder jetting is needed to verify this assumption. Additionally, the structural analysis in Section 2 showed that the TO components exhibit structural behaviour that is comparable to the standard component, while the presence of compressive yield magnitude residual stresses in the TO1 bracket, ought to be considered in the optimisation process.

Effectively, the next steps of this research entail the feeding back of the structural and residual stress analyses in the TO process, as well as a detailed AM carbon footprint analysis that considers binder deposition, powder bed, binder drying, curing, de-binding, and sintering times. Computing a bracket geometry informed by residual and structural stresses that takes a minimum amount of time to fabricate is the next aim of this project.

Appendix

Fig. 21

The TO1 bracket following horizontal loading up to failure

Fig. 22

The TO2 bracket following horizontal loading up to failure

Fig. 23

The TO3 bracket following horizontal loading up to failure

Fig. 24

The TO4 bracket following horizontal loading up to failure

Fig. 25

The F5 bracket following horizontal loading up to failure

Fig. 26

The F6 bracket following horizontal loading up to failure

Fig. 27

The F7 bracket following horizontal loading up to failure

Fig. 28

The TO1 bracket following vertical loading up to failure

Fig. 29

The TO2 bracket following vertical loading up to failure

Fig. 30

The TO3 bracket following vertical loading up to failure

Fig. 31

The TO4 bracket following vertical loading up to failure

Fig. 32

The F5 bracket following vertical loading up to failure

Fig. 33

The F6 bracket following vertical loading up to failure

Fig. 34

The F7 bracket following vertical loading up to failure