1 Introduction

Large positive Magnetoresistance (LMR) effects have attracted much attentions and widely studied in past few decades in different quantum materials system with the mechanisms remains unclear [1–4]. For example, in Fe/Cr multilayers and some Mn-based oxides, giant \(\mathrm{MR}(\mathrm{GMR}, 100\%)\) and colossal MR (CMR, ∼104%) had been discovered and made great contributions to spintronics [5]. In recent years, large MR was also found in narrow band-gap semiconductors, topological insulators, disorder systems, and Dirac electron systems, such as in MnAs-GaAs nanoparticles and films [6], \(\mathrm{Ag}_{2+\delta }(\mathrm{Se},\mathrm{Te})\) (\(\delta \sim 0.01\)) and Sb-rich InSb [7–10], nonmagnetic graphene [11], Bi2Te3 nanosheets [12], Bi2Se3 topological insulator thin films [13], Bi2Te3/Bi2Se3 heterostructures [13], strong topological insulator TaAs2 [14], Dirac fermions Cd3As2 [15], Weyl fermions TaAs, WTe2 [16–18], and so on. Semiclassical magnetoresistance (MR) is a natural solution of the Boltzmann equation for MR, which means that a conductor in an applied magnetic field (H) shows MR that grows quadratically with H and moreover, will saturate to a relatively small constant value at high H. Quantum MR (QMR) exhibits linear increase with H and does not saturate even at very high H. The QMR has a generic quantum description by \(\omega = 1/[\sigma ^{2}(F_{0}^{2}) + 0.00739(F_{0})^{2}]\) proposed by Abrikosov in 1969 [1], where \(\rho _{xx}\) and \(\rho _{yy}\) represent the transverse components of MR, n is the density of electrons, and \(N_{i}\) is the concentration of static scattering centers. From a viewpoint of practical application, the relatively larger QMR(LQMR) owing to the virtue of non-saturating for device and sensor applications is also very attractive. Unfortunately, real stoichiometric bulk compounds hosting the LMR are still very rare and the origin of LMR remains puzzle.

Recently, a new family of topological materials LnPn compounds, where Ln represent alkali-earth metal, and Pn represents P, As Sb or Bi elements, were predicted to possible existed large MR and topological quantum effects, such as the quantum anomalous Hall effect, Majorana bound states, and superconductivity [19]. For example, a band inversion between lanthanum d-orbitals and pnictogen p-orbitals at X-point appears in all five lanthanum monopnictides LaN, LaP, LaAs, LaSb and LaBi [20]. In their work, LaP was predicted to be 3D TI with multi-valley surface Dirac cones. Angle-resolved photoemission spectroscopy (APRES) experiments gave evidence of bands in LaBi [21] while trivial band topology in LaSb and LaAs [22–24]. As far as we know, there is no ARPES or transport results reported in topological insulator candidate LaP. Previous reports on the synthesis of LaP are limit to polycrystalline samples, and the physical properties were seldom studied [25]. Therefore, it is challengingto grow LaP single crystal and study the interplay between novel quantum states and exotic transport properties like large MR, quantum Hall effect etc.

In this work, we successfully grew pure single phase LaP single crystals with NaCl type structure, and carried out detailed studies on its structure and basic physical properties. We found large positive magnetoresistance (LMR) of 500% appears at 2 K, 9 T in LaP. The Hall effect measurements show that the conduction carriers are dominated by holes among the temperature range from 300 K to 2 K, which probably origin from the large hole pocket near Γ point. The carrier concentration \(n_{h} =4.94\times 10^{19}\) cm−3 and \(n_{e} =5.02\times10^{16}\) cm−3 are obtained at 2 K, while the mobilty of LaP reached as high as \(\mu _{h}=1.57\times10^{4}\) cm2 V−1 S−1 and \(\mu _{e} = 1.55\times10^{3}\) cm2 V−1 S−1. LaP shows no evidence of phase transition over a wide temperature range from 2 K to 300 K from susceptibility measurement and specific heat measurements. The electronic specific heat coefficient is obtained 0.538 m J mol−1 K−2 for LaP single crystal, which responds to a small electron density state near the Fermilevel.

2 Experiment section

The synthesis of crystalline LaP was grown by a flux method based on procedures of previously published paper [23]. The starting materials, La powers (99.999%, Alfa), P lumps (99.999%, Alfa) and Sn were mixed with the mole ratio 1:2:22 in an Al2O3 capsules which were sealed with appropriate amount Ar atom into a silica tube. The whole silica tube was then quickly heated up to 1273 K in a furnace and maintained at this temperature for 20 hours. Then the sample was slowly cooled down to 973 K at the speed of 1 K/hour where the flux was spun off by a centrifuge. Cubic black crystals with shining surface and a typical size of 2 × 1 × 1 mm3 were finally left, shown by the optical microscopy picture in Fig. 1(d). The crystals were unstable in the air for more than one week. The crystallographic information framework (CIF) file from a previously published work [25] was used for structural refinement. To confirm the stoichiometry, chemical compositions of the crystals were confirmed by energy dispersive x-ray (EDX) spectroscopy equipped on a Hitachi S-4800 scanning electron microscope (SEM). The crystals were characterized by X-ray diffraction (XRD) at 300 K on a Bruker SMART APEX II diffractometer using Cu \(K_{\alpha}1\) radiation (\(\lambda = 1.5406\) Å). The crystal structure data were solved using SHELXT with intrinsic phasing and refined with SHELXL-2014/7 via the full-matrix least-squares fitting [26]. The temperature dependence of magnetization was measured using a vibrating sample magnetometer (VSM-7 T, Quantum design). The measurements were taken under zero-field-cooled and field-cooled conditions in the temperature range 2 K–300 K and in the applied magnetic fields of 10 K Oe. Isothermal magnetization curves were recorded between magnetic fields of ±70 K Oe at temperatures of 2 K and 300 K. A standard four probes method were used to perform resistivity measurements. Four platinum leads were attached onto a plate-shaped crystal with dimensions of 1.00 × 0.2 × 0.10 mm3. A constant current of 1 mA was applied to the sample along the ab plane through the two outer leads. The temperature dependence of the specific heat (Cp) was measured on a physical properties measurement system (PPMS-9 T, Quantum Design) using the \(H_{C}\) option (relaxation method).

Figure 1
figure 1

(a) Crystal structure of LaP, where the red, the yellow represent La, P atoms respectively (b) single crystal X-ray patterns of LaP with \((0\ 0\ l)\) plane. (c) Optical image of the typical LaP single crystal in single-crystal X-ray diffraction measurements

Full size image

3 Results and discussions

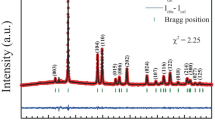
The single-crystal x-ray diffraction (SCXRD) collected in this paper can be well refined in the NaCl type structure with Fm-3m (No. 225) symmetry, as shown in Fig. 1(a). The best fit does not reveal any significant impurity contribution in the studied crystals. The detailed crystallographic data of LaP are summarized in Table 1. Atomic positions and temperature factors for LaP obtained from the refinements of the SCXRD data are summarized in Table 2. The large surface of crystals characterized by single crystal X-ray diffraction (XRD) indicated the \([0\ 0\ l]\) direction of the large face. The structure refined results, listed in Tables 1 and 2, indicating a stoichiometric composition. The typical size of LaP single crystal is 1 mm × 1 mm × 0.5 mm, an optical image shown in the inset in the Fig. 1(b). The composition was checked by the energy dispersive x-ray (EDS) spectroscopy. The results show that the chemical ratios of LaP crystals are 1:1 within the experiment accuracy of 5%.

Table 1 Refined crystallographic parameters of LaP from single crystal x-ray structure analysis at 293(2) K
Full size table
Table 2 Atomic coordinates and equivalent isotropic thermal parameters of LaP
Full size table

The temperature dependence of resistivity \(\rho _{xx}\) with the current I perpendicular to the \([0\ 0\ l]\) direction under zero magnetic field for LaP crystals is shown in Fig. 2(a). The residual resistivity at 2 K is rather small, which is only about 0.037 mΩ cm, shows a semimetal behavior in the scale of 10−1 mΩ cm. The residual resistivity ratio RRR (\(=\rho (300\text{ K})/\rho (2\text{ K})\)) for LaP crystals along \([0\ 0\ l]\) directions, ∼ 21, are smaller than the values of normal metals of these series whose RRR are typically much larger than 100, but still shows metallic behaviors. If we define \(\mathrm{MR}= [(\rho (H) - \rho (0))/ \rho (H)]\), we can plot MR as a function of temperature in Fig. 2(b). In traditional metal without magnetism, the MR effect is usually a few percentages and quickly saturated under a weak magnetic field. However, in nonmagnetic metal LaP, the large magnetic and temperature dependent MR can be observed, beginning from 2 K and increases to its maximum of 500% at around 2 K, 9 T. After that, the MR drops again with decreasing temperature. The MR magnitude of LaP is smaller than reported LaX series compounds with NaCl structure type, like LaAs[1 × 104% at 2K 9T] [24], LaSb [1 × 106% at 2K, 9T] [22, 23] and LaBi (5 × 105% at 2 K, 9 T) [21]. The reason might be that the quality of LaP single crystal is bad than the LaAs, LaSb and LaBi. Judging from the residual resistivity ratio RRR, we think more defects in LaP single crystal. It was proposed that the LMR property in LnX(X = N, P, As, Sb, Bi) compounds come from carrier compensation or the nontrivial band dispersion [22]. From the Hall slope \(R_{H}=-1/n_{e}\) of the data shown in Fig. 2(c), we could confirmed that hole dominates the transport behavior. Electron density carriers change a little below 300 K. In low temperature range below 75 K, the Hall shows anomalous behavior. The carrier density at 2 K can be deduced from Hall data with multiband band model: \(n_{h} =4.94\times10^{19}\) cm−3 and \(n_{e} =5.02\times10^{16}\) cm−3. While according to the Drude conductivity \(\sigma = \mathrm{ne}\mu \), the effective electron and hole mobility is then \(\mu _{h}=1.57\times10^{4}\) cm2 V−1 S−1 and \(\mu _{e} = 1.55\times10^{3}\) cm2 V−1 S−1. While in high temperature range above 75 K, a single hole band dominates in transport with weakly temperature-dependent carrier density and mobility. which means the effective electron mobility fluctuations might play a key role in the temperature dependent MR behavior.

Figure 2
figure 2

The transport properties of LaP single crystal (a) the temperature dependence resistivity \(\rho _{xx}\) in the absence of an applied magnetic field from 2 K to 300 K with current along the \((1\ 0\ 0)\) plane. (b) The field-dependence magnetoresistance (MR) for various temperatures (2 K, 5 K, 10 K, 25 K, 100 K 200 K & 300 K) on sweeping applied field from 9 T to −9 T while the apply magnetic field is along \((0\ 0\ 1)\) plane. (c) The Hall data of LaP for various temperatures (2 K, 5 K, 10 K, 25 K, 100 K 200 K & 300 K) on sweeping applied field from 9 T to −9 T. (d) Carrier concentration and carrier mobility extracted from normal Hall resistivity from 2 to 300 K. In LaP, the concentration of electrons reaches 1018 cm−3 and the mobility reaches as high as about \(1.57\times 10^{4}\) cm2 V−1 s−1

Full size image

Figure 3(a) shows the temperature-dependent magnetic susceptibility \(\chi (T)\) of LaP. The \(\chi (T)\) displays almost temperature independent above 20 K and then steeply increases upon further cooling below 20 K. Neither anomalies signifying magnetic orderings nor clear abruptions between the ZFC and FC curves are visible. The magnetization over the temperature range is negative, consistent with the expectation of diamagnetic behavior in a massless 3D Dirac ffermion system because of contribution from orbital Landau diamagnetism, like LaSb, LaAs and LaBi [21, 22, 24]. However, the \(\chi (T)\) is in fact very weak, for example, χ(2 K) is only about \(-0.25\times 10^{-4}\) emu mol−1 in \(H = 10\) k Oe, somewhat different from the theoretical prediction of giant diamagnetism in topological insulators [17] possibly due to the significant contribution from the spin component of Pauli paramagnetism that somewhat masks the orbital diamagnetism. The diamagnetic behavior is also confirmed by the isothermal magnetization shown by the Fig. 3(b) measured at 2 K and 300 K. No clear hysteresis loops are visible in \(\chi (H)\) curves at both temperatures.

Figure 3
figure 3

The Field-dependent and temperature-dependent magnetic properties of LaP. (a) Magnetic susceptibility of ZFC and FC as a function of temperature measured in an external field of \(\mu _{0}\text{ H} = 1\text{ Tesla}\). (b) The field-dependent magnetization χ-H curve for 2 K to 300 K, respectively

Full size image

Temperature dependent specific heat (\(C_{p}(T)\)) of LaP crystal is presented in Fig. 4 by the main panel. \(C_{p}(T)\) changes rather monotonically without showing any anomalies, suggesting the absence of any structural transitions in the temperature range from 300 K to 2 K. The \(C_{p}(300\text{ K})\) is approximately 44.36 J mol−1 K−1, close to the value estimated from the classical Dulong-Petit heat capacity \(C_{p }= 3nR \approx 44.94\) J mol−1 K−1, where \(n = 2\) is the atoms number of per formula unit and \(R=8.314\) J mol−1 K−1 is the molar gas constant [27]. The low-temperature specific heat in the form \(C_{p }/T\) vs. \(T^{2}\) below 10 K is shown by Fig. 4(b). The linear trend of the plots at very low temperatures indicates that the Debye approximation may characterize the temperature dependence of \(C_{p }\). The least-squares analysis to the linear part using the formula \(C_{p }/T = \beta T^{2} + \gamma \), where β and γ are the lattice and electronic contributions to the \(C_{p }\), respectively, yielded \(\gamma \approx 0.568\) mJ mol−1 K−2. The γ value indicates considerable density of states (DOS) on the \(E_{F}\), consistent with the theory calculation results [20]. The non-zero γ value shows really small considerable density of states (DOS) at \(E_{F}\), indicating the electronic correlations in LaP is quite weak.

Figure 4
figure 4

(a) The specific heat coefficient Cp/T as a function of T for LaP. (b) The fitting curve of the low-temperature specific heat in the form \(Cp/T\) vs. \(T^{2}\) below 10 K with formula \(C_{p }/T = \beta T^{2} + \gamma \)

Full size image

The above physical properties of LaP could be understood in the frame of electron band structure. We search the topological material database online [28–30]. With different DFT calculated methods, different databases give confusing judgements about whether LaP is topological nontrival or not. In ref [28], LaP is defined as gapless TI with nontrivial topological invariant \(Z_{2}=1\); \(Z_{4}=1\), the conduction bands at X point cross the Fermilevel. While in ref [29], LaP was defined as trivial insulator whether in the situation of considering SOC effect or not. Another database [30] shows LaP owns an indirect band gap with 4 meV with GGA calculated method. As there are no Berry phase related quantum oscillations observed in our transport data, we cannot define the topological properties from Landua index fan or Berry phase factor. Perhaps further improvement of single crystal quality will be helpful to APRES and transport experiment to determine whether LaP is TI with multi-valley surface Dirac cones or not.

4 Conclusion and outlook

In conclusion, we reported the growth of pure single phase LaP single crystal by flux method. Form the electron transport measurements, we discover large positive MR(LMR) about 500% at 2 K, 9 T. The Hall effect measurements show that the conduction carriers are dominated by holes among the temperature range from 300 K to 2 K, the carrier concentration \(n_{h} =4.94\times 10^{19}\) cm−3 and \(n_{e} =5.02\times 10^{16}\) cm−3 and the mobility of LaP reached as high as \(\mu _{h}=1.57\times 10^{4}\) cm2 V−1 S−1 and \(\mu _{e} = 1.55\times 10^{3}\) cm2 V−1 S−1 obtained at 2 K by two band model fitting. No magnetic phase transition over a wide temperature range from 2 K to 300 K was observed from the heat capacity and susceptibility measurements. Our observations of the significant large MR and high mobility in LaP are instructive to search for large MR topological materials and serves as a platform for understanding the interactions between large magnetoresistance, high mobility and topological band structure, which would also be very useful for device applications.