1 Introduction

For type-II superconductors, magnetic field can partially penetrate the bulk and form quantized vortices which arranged in Abrikosov lattice [1] [Figs. 1(a)-(b)]. The order parameter Δ at the vortex core center is zero, while it gradually increases to its normal value as leaving the core, therefore the vortex acts as a “potential well” for superconducting quasi-particles [Fig. 1(a)]. In the 1960s, Caroli et al. have predicted that for conventional s-wave superconductors, there are localized bound states in the vortex core, which was called Caroli-de Gennes-Matricon (CdGM) bound states [2]. These states have discrete energy levels with an approximate expression of \(E_{\mu} =\mu \Delta ^{2} / E_{F}\). Here μ is the quantum number of orbital angular momentum, which is a half integer (±1/2, ±3/2, …); \(E_{F}\) is the Fermi energy and Δ is the size of superconducting gap. It is seen that the energy levels of CdGM states locate symmetrical with respect to \(E_{F}\), but there is no zero-energy state [Fig. 1(c)]. Later on, Volovik [3], Read and Green [4] found that for chiral p-wave superconductors [\(\Delta _{k} =\Delta ( k_{x} +i k_{y} )\)] or superfluid, the bound states energy in the vortex core can still be written as \(E_{\mu} =\mu \Delta ^{2} / E_{F}\), but μ becomes an integer (0, ±1, ±2, …) [Fig. 1(d)]. This is because its chiral order parameter produces additional phase, which changes the boundary conditions of quasi-particle wave functions in the vortex. It is known that the bound state at \(E=0\) is essentially the Majorana zero mode (MZM).

Figure 1
figure 1

(a) Sketch of a vortex in superconductor; (b) Vortex lattice measured on NbSe2 [5]; (c) The distribution of CdGM states in the vortex core of s-wave superconductor [6]; (d) The distribution of low-energy vortex bound state of chiral p-wave superconductor [7]; (e) Majorana Zero modes in semiconductor nanowire/superconductor system [8]; (f), (g) The vortex image and spin-resolved \(dI/dV\) spectrum of in Bi2Te3/NbSe2 heterostructure [9]; (h) The vortex zero modes observed in Fe(Te,Se) [10]

Full size image

A Majorana quasi-particle is its own antiparticle, which can be considered as a mixture of particle and hole state [11–16]. In superconductors, generating an electron is equivalent to generating a hole together with a Cooper pair. The hole and electron state can form a quantum superposition state (Bogoliubov quasiparticles). Therefore, it is possible to find Majorana quasi-particle in superconductors. For a spin singlet pairing state, the spins of the two electrons are opposite, which does not satisfy the Majorana symmetry. However, for spin-triplet pairing, the electron spins can be the same, and thus Majorana quasi-particle can be generated in certain conditions. E.g., MZM appears in the vortex core of a chiral p-wave superconductor.

MZM is the simplest quasi-particle state that obeys non-Abelian statistics, which can be used to construct topological qubits and realize fault-tolerant topological quantum computation [17, 18]. The appearance of MZM usually indicates the superconducting system is topological nontrivial. Such important application of MZM has greatly stimulated the research on topological superconductors and their boundary states. However, it is challenging to realize intrinsic p-wave superconductor experimentally. In 2008, Fu and Kane [19] proposed a model which is easy to implement: if the s-wave superconductor is coupled with the spin-helical topological surface state, the effective Hamiltonian of the system is equivalent to the spinless chiral \(p+ip\) wave superconductor, and a single MZM can be observed in the vortex core. After that the model was also extended to one-dimensional (1D) system [11–14]. Experiments based on this assumption have been carried out rapidly. At present, many important signs of MZMs have been observed in the heterostructures of s-wave superconductors and topological insulator films [9, 20–22], such as the Bi2Te3/NbSe2 heterostructure shown in Figs. 1(f) and (g) [9], and coupled 1D chain systems (such as semiconducting nanowires, magnetic atom chains) with superconductors shown in Fig. 1(e) [8, 23–26].

In this review, we mainly discuss the MZM residing in the vortex cores. As mentioned above, the study of vortex bound states actually has a long history. To look for MZMs, one needs to detect the localized zero-energy states. Scanning tunneling microscopy (STM) is well suited to probe local electronic states at extremely low temperature and strong magnetic field [27]. However, vortex states with discrete energy have only been observed recently because of the tiny energy spacing between them, which is expected to be \(\Delta ^{2} / E_{F}\). For conventional superconducting metals/alloys, the typical value of \(\Delta ^{2} / E_{F}\) is only 1 μeV, which is much smaller than the energy resolution of the lowest temperature STM at present. In addition, if there are strong impurity scatterings, the energy levels will be broadened and become more difficult to be distinguished. For example, Hess et al. [5, 28] only observed a broad zero bias peak at the NbSe2 vortex core, and the zero bias peak began to split when moving away from the vortex center. However, in theory the energies of any vortex states shall not change with the distance, while their intensities show damped oscillation with a period of Fermi wavelength [Fig. 1(c)]. When μ is large, \(E_{\mu} \) has the maximum intensity at \(r_{\mu} \sim \vert \mu \vert / k_{F}\) [6]. Therefore, the “splitting” zero bias peak in NbSe2 is the envelope of bunched vortex states. Similar phenomena are commonly observed in many other superconductors [29–31].

In recent years, the emergence of iron-based high-temperature superconductors provides a new platform to study vortex bound states and even topological superconductors. These materials have narrow energy bands, small \(E_{F}\) and relatively large, fully opened superconducting gaps, which means they are favorable for the observation of vortex bound states. Particularly, many iron-based superconductors are predicated to have topologically nontrivial band structures [32–35]. Recently, discrete vortex bound states and zero-energy modes were indeed observed in Fe(Te,Se) [Fig. 1(h)] [10, 36–38], together with topological surface state [39]. This suggests Fe(Te,Se) itself satisfies the Fu-Kane model and is a topological superconductor.

Generally, to find clear MZM signatures in the vortex, the conditions listed below are preferred: 1) An intrinsic topological superconductor or superconductor with topological edge state which satisfy the Fu-Kane model. 2) Relatively small \(E_{F}\) and large superconducting gap, which benefits the measurements and also the stability of MZM. 3) Short superconducting coherence length to weaken the interaction between adjacent vortices [40]. 4) Stoichiometric superconducting layers to reduce local disorders and impurities.

It should be emphasized that the zero-bias conductance peak (ZBCP) does not necessarily originate from MZM, some other effects can also generate zero or near-zero energy mode, such as Yu-Shiba-Rusinov states [41], Kondo resonance [42] and SIS tunneling [43]. It is important to exclude trivial zero energy states by checking the characteristics of MZM, such as quantized conductance [44–46] and spin-polarization [7, 9, 25, 47, 48]. The spatial distribution of vortex states can also provide valuable information on their origin. Furthermore, a comparative study of iron-based superconductors with different band structures is helpful to understand the nature of zero-energy states.

The following part of this review includes several studies on the vortex states of (Li,Fe)OHFeSe and single-layer FeSe/SrTiO3 [49–52], which are belong to electron-doped FeSe-based superconductors. The former shows clean ZBCP in the unpinned (free) vortex cores, and exhibits a characteristic of Majorana zero mode, that is, a conductance close to quantized value. The ZBCP shows distinct spatial distribution with respect to the nonzero energy mode and indicates its different electronic origin. Angle-resolved photoemission spectroscopy (ARPES) observed a Dirac cone-type surface state and DFT/DMFT calculations suggest its topological nature. Therefore, the observed ZBCP can naturally be attributed to a MZM arising from topological surface state on a bulk superconductor. Meanwhile, single-layer FeSe/SrTiO3 has only conventional CdGM states without ZBCP, which is a typical behavior of s-wave superconductors. These results not only provide strong evidence of MZM in FeSe-based high \(T_{C}\) superconductors, but also reveals its possible origin.

2 Band structure and observation of vortex zero-mode in (Li, Fe)OHFeSe

Iron-based superconductors are multi-band systems with numerous members and abundant physical properties. In 2014, Hao and Hu [32] predicted the existence of topological nontrivial band structures in FeSe and similar calculation was applied to FeSe1-xTex [33, 34]. (Li, Fe)OHFeSe is an intercalated heavily electron-doped FeSe-based superconductor [53–56] with \(T_{c}\) up to 42 K. The corresponding crystal structure of this material is shown in Fig. 2(a). In reference [49], Liu et al. presented the band structure calculation of (Li0.75Fe0.25)OHFeSe using density functional theory combined with dynamical mean-field theory (DFT + DMFT) [57, 58]. The calculated results show that (Li, Fe)OHFeSe system can have topological surface state and topological nontrivial bulk band which matches the Fu-Kane model.

Figure 2
figure 2

Band structure and topological surface states of (Li1-xFex)OHFeSe. (a) The crystal structure and bulk & (001) surface Brillouin zone of (Li, Fe)OHFeSe; (b) Calculated Band structure of (Li0.75Fe0.25)OHFeSe along \(M\text{-}\Gamma \text{-}Z\text{-}(R)\) direction; (c) Calculated bulk and Dirac-cone-like topological surface states on the (001) surface along the \(\overline{\Gamma} - \overline{M}\) direction; (d) Photoemission intensity near \(E_{F}\) across Γ̅ along cut #1 in panel (a); (e) Second derivative of the photoemission intensity in the marked region of panel (d); (f) \(E-k\) dispersion extracted from the data [49]

Full size image

As shown in Fig. 2(b), (Li0.75Fe0.25)OHFeSe has three flat bands and one obviously dispersive band around the Fermi level along the Γ-Z direction. The former bands are dominated by the Fe \(3d_{xy}\), \(3d_{yz}\) and \(3d_{xz}\) orbitals. The latter dispersive band is composed by the Se \(4p_{z}\) orbital and the Fe \(3d_{z}^{2}\) orbital in the (Li, Fe)OH layer. It crosses the Fermi level and the Fe 3d bands along Γ-Z, giving rise to a nontrivial band inversion and band topology. Here Fe atoms in (Li, Fe)OH layer play a crucial role as they strongly hybridize with the Se \(4p_{z}\) orbital and change the dispersion and position of the Se \(4p_{z}\) band. Combined with spin-orbital coupling (SOC), a hybridization gap opens along Γ-Z with a size of 2.5 meV. Further calculations demonstrate that Dirac-cone-like surface states centered at Γ̅ point appear on the (001) surface as shown in Fig. 2(c). Such topological surface states have helical spin texture and can support MZM in vortex core when it becomes superconducting [19].

ARPES measurements were conducted on high-quality (Li0.84Fe0.16)OHFeSe samples prepared by matrix-assisted hydrothermal epitaxy [59, 60]. The ARPES spectrum near Γ̅ point across the Brillouin zone (BZ) center and the calculated ones in Fig. 2(b) have a qualitatively one-to-one correspondence. The relative positions and bandwidths may differ because of correlation effects. Importantly, some finite spectral weights were resolved within the bulk band gap around Γ̅ near the Fermi energy as shown in Fig. 2(d). The second derivative of the region containing this spectral weight [Fig. 2(e)] displays a nearly linear, Dirac-cone-like band dispersion. Therefore, it is likely the topological surface state predicted in calculations. Some other possible scenarios can be ruled out here, such as the band in the (Li1-xFex)OH surface layer [61] or the electronlike pocket around Γ̅ after heavily electrons doping [62]. The dispersion of the surface states is obtained by fitting the momentum distribution curves (MDCs) as shown in Fig. 2(f).

The superconductivity and vortex states of (Li,Fe)OHFeSe were detected by low temperature STM at \(T = 0.4\text{ K}\). Figure 3(a) is the typical topography of a cleaved (Li0.84Fe0.16)OHFeSe film which contains FeSe- and (Li,Fe)OH-terminated surfaces. Figure 3(b) shows the typical tunneling spectrum on FeSe surface. It displays a U-shape superconducting gap with two pairs of coherence peaks (\(\Delta _{1}\) and \(\Delta _{2}\)) and a flat bottom. On (Li,Fe)OH surface, the tunneling spectrum is metallic without superconducting gap. There are dumbbell-like defects on the FeSe surface, which could be Fe vacancies or substitutional impurities. They can induce strong impurity states in the superconducting gap. Quasiparticle interference (QPI) measurements revealed electronlike pockets with a band bottom at \(-57\text{ meV}\) and \(k_{F} = 0.21~\mathring{\mathrm{A}}^{-1}\) [Fig. 3(i)], consistent with the ARPES measurements.

Figure 3
figure 3

Topography, superconducting gap, and vortex bound states of (Li0.84Fe0.16)OHFeSe: (a) Topographic image of a cleaved film. Inset: the lattice of FeSe surface; (b) Typical \(dI/dV\) spectra taken on FeSe and (Li, Fe)OH surface; (c) \(dI/dV\) spectra taken across a free vortex; (d) Color plot of the spatial dependence of the \(dI/dV\) spectra shown in panel (c); (e) \(dI/dV\) spectra taken at the small range near the vortex; (f), (g) Summed low-energy \(dI/dV\) spectra taken near the centers of Vortex 1–2. Red solid curves are the fits to multiple Gaussian peaks. (h) zero bias conductance map on FeSe surface under \(B = 10\text{ T}\); (i) electron-like Energy dispersion measured by QPI at M̅ point [49]

Full size image

Under a magnetic field of 10 T perpendicular to the surface, vortex cores are visible on the zero-bias-conductance (ZBC) map [Fig. 3(h)]. Figure 3(c) shows the tunneling spectrum measured across the unpinned free vortex center (inset image, free vortex refers to the vortex which is not pinned by surface impurity). Discrete peaks are observed near the core center and there is one peak located right at zero bias (a ZBCP). There are several non-zero energy peaks distributed around ZBCP symmetrically. The energy spacing between these peaks is near 1 meV. Figure 3(d) presents the spatial evolution of the spectra in a color plot. When leaving the core center, the intensities of these discrete peaks decrease and vanish at about 2 nm away, and then a pair of much broader peaks [shaded regions in Fig. 3(c)] show up and gradually shift to higher energies, giving an X-shaped pattern. The nonzero peaks may slightly change their position as leaving the vortex core, but the ZBCP is always located at zero bias.

Such discrete peaks including ZBCP can be repeatedly observed in other free vortices. At zero field, clear U-shaped superconducting gaps are observed in the vortex locations, which ruled out these peaks are impurity states. These low-energy discrete peaks can only be vortex bound states which should have an energy spacing of \(\delta E= \Delta ^{2} / E_{F}\). For (Li0.84Fe0.16)OHFeSe, as we have measured \(\Delta \approx 10\text{ meV}\), \(E_{F} \approx 57\text{ meV}\), then δE is estimated to be 1-2 meV, which matches the observed value. The broad “shifting” peaks can be attributed to the envelope of closely packed high-level states, since the spacing between high-level states will decrease and make them indistinguishable. Therefore, both discrete low-level core states and the quasi-continuous high-level states are observed, benefitting from the large δE here and sufficiently energy resolution at 0.4 K.

The ZBCP (\(E_{0}\) state) is the most important discovery of this experiment. Compared with other nonzero-energy peaks, the ZBCP is more robust (independent of the position) and its broadening is smaller than other peaks, which suggest its unusual origin. As band calculations and ARPES measurements suggest (Li0.84Fe0.16)OHFeSe has non-trivial band structure and topological surface states, the proximity effect induced superconductivity in surface states will naturally generates MZMs in vortex cores. Meanwhile, bulk electron band should also induce its own vortex states (CdGM states), which explains the nonzero energy peaks observed here. Other effects may lead to a ZBCP such as the Kondo effect, SIS (superconductor-insulator-superconductor) tunneling can be here excluded since there is no impurity in free vortex and the tip is non-superconducting. We also checked other pairing symmetries such as \(s_{\pm} \), \(\text{d} + \text{id}'\), and nodeless d-wave will not lead to a robust ZBCP. Therefore, the MZM generated by topological surface states is the most likely origin of the robust ZBCP.

3 Quantized conductance of the vortex zero modes in (Li0.84Fe0.16)OHFeSe

A ZBCP in tunneling spectroscopy is important evidence, but not sufficient proof for identifying MZM. One of more compelling evidences is the quantized conductance induced by resonant Andreev reflection of MZM [44, 45]. Such process can be understood by means of conventional resonant tunneling [Fig. 4(a)]. Considering an electron tunneling from one lead through a quantum dot into the other, if the barrier between the first lead and the dot is equals to that between the dot and the second lead, perfect transmission can be achieved regardless of the barrier strength. As for superconductors, incident electrons on the interface will have probability to reflect as a hole, while two electrons are transmitted into the superconductor to form Cooper pair (Andreev reflection). In STM experiments, the tip can play the role of both an electron lead and a hole lead [Fig. 4(b)]. Due to the fact that a MZM is its own antiparticle, the particle and the hole are equivalent and the tunneling barriers they experienced will be the same, thus the resonance condition is satisfied. Such resonant Andreev reflection leads to a quantized conductance (\(G_{0} =2 e^{2} /h\)) at zero temperature. For other nonzero bound states, they do not satisfy resonant tunneling condition and do not have the quantized conductance.

Figure 4
figure 4

Resonant Andreev reflection and quantized conductance of MZM: (a) Conventional resonant tunneling [45]; (b) Majorana zero mode induced resonant Andreev reflection (MIRAR) [45]; (c), (d) The relationship between MZM conductance (G) and temperature (T), tunneling coupling (Z is proportional to the tunneling barrier strength) [46]

Full size image

In actual measurements, zero temperature cannot be reached, and the conductance peak will have temperature broadening (\(= 3.5k_{B} T\)). At finite temperature, theoretical simulations [46] show that the quantized conductance can still be observed when the tunneling coupling is sufficiently strong [Figs. 4(c) and (d)]. This means the temperature and tunneling barrier should be reduced as much as possible in experiment. Because the STM generally works at relatively weak tunneling coupling (high tunneling barrier). It will require lower experimental temperature. In Ref. [50], a millikelvin STM study (\(T_{\text{eff}} = 160\text{ mK}\)) on the ZBCP in vortex core of (Li0.84Fe0.16)OHFeSe is carried out.

Figure 5(a) shows the tunneling spectrum of the vortex core at \(\text{T}_{\text{eff}} = 160\text{ mK}\). Compared with the result in Fig. 3, the ZBCP becomes much sharper and a Lorentzian fit gives the full width at half maximum (FWHM) of 0.10 meV. The \(dI/dV\) spectra taken across a free vortex core are shown in Fig. 5(b). It can be seen that the ZBCP does not shift upon leaving the core. Meanwhile, other discrete vortex states can be clearly resolved, revealing finer structures of the off-zero-bias vortex states.

Figure 5
figure 5

(a) Red curve: \(dI/dV\) spectrum at the core center. Blue dashed curve is the Lorentzian fit to the ZBCP; (b) Spatial dependence of the \(dI/dV\) spectra in panel (a); (c) evolution of the \(dI/dV\) spectra as a function of increased \(G_{N} = I_{\mathrm{set}} / V_{b}\); (d)–(g) selected \(\text{d}I/\text{d}V\) spectra taken at different \(G_{N}\) for Vortex 2; (h) The zero-bias conductance as a function of \(G_{N}\) [50]

Full size image

It should be pointed out that the absolute value of \(dI/dV\) spectrum is important to acquire actuate tunneling conductance of ZBCP. Here we calibrated the lock-in measured \(dI/dV\) by numerical differentiation of the I/V curve, and the wire resistance of the tunneling loop is checked and excluded. The errors caused by other electronic devices, such as the internal resistance of the bias divider are also eliminated.

The ZBCP in Fig. 5(a) is measured at a high tunneling barrier (\(R_{N} = 5\times 10^{7}\Omega \)), its absolute conductance is still much lower than the quantized value \(G_{0}\) (\(2 e^{2} /h = 7.7\times 10^{-5} \Omega ^{-1}\)). To enhance the tunneling coupling, the distance between the STM tip and the sample surface is gradually reduced. This is achieved by increasing the setpoint tunneling current \(I_{\mathrm{set}}\) at fixed bias voltage \(V_{b}\). \(G_{N} = I_{\mathrm{set}} / V_{b}\) is defined here to reflect the transmissivity of the tunneling barrier. Figure 5(c) shows a series of \(dI/dV\) spectra taken with increasing \(G_{N}\). At low \(G_{N}\), the conductance of ZBCP increases rapidly; while at high \(G_{N}\), the ZBCP conductance saturates around \(G_{0}\) over an extended \(G_{N}\) range. Particularly, when \(G_{N}\) is large enough (Figs. 5(f,g)), the \(dI/dV\) starts to show a dip or double-peak feature near EF. However, the zero-bias conductance remains around \(G_{0}\) within a certain range while the two side peaks significantly exceed \(G_{0}\). Such intriguing behavior would suggest a nontrivial origin of ZBCP.

Figure 5(h) summarizes the zero-bias conductance as a function of \(G_{N}\) from extensive set of \(dI/dV\) spectra. A nearly quantized conductance plateau is observed around \(G_{0}\), which provides additional evidence of MZM. We note the zero-bias conductance continues to increase at high \(G_{0}\), which may be due to the contribution of non-zero bias vortex states. This is because all the vortex states peaks are expected to be broadened at strong tunneling coupling, and they could overlap with each other and contribute additional conductance at zero bias. Overall, the nearly quantized conductance of ZBCP further supports the existence of MZM in (Li0.84Fe0.16)OHFeSe. We note similar quantized conductance of ZBCP was also observed in the vortex core of Fe(Te,Se) system [63]. These results are helpful to further understand the physical properties of MZM.

4 The spatial distributions of vortex state in (Li0.84Fe0.16)OHFeSe

Besides the energy spectrum, the spatial distribution of vortex bound states also carries important information about superconducting state. In reference [52], T. Z. Zhang et al. used low-temperature STM to measure the spatial properties of the vortex state in (Li,Fe)OHFeSe. Theoretically, the wave functions of individual bound states decay exponentially away from the vortex center in a scale of coherence length (ξ), while they oscillate with a period of Fermi wavelength (\(\lambda _{F}\)). Such spatial oscillations are expected to be asymmetric for particle and hole states, depending on the specific band structure [6, 7, 48]. However, to observe these fine structures one needs both high energy and spatial resolution, since the energy spacing of vortex states is small.

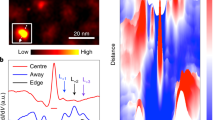
In reference [52], STM measurements were conducted in a dilution refrigerator STM with \(T_{\text{eff}} = 160\text{ mK}\). The tunneling spectrum of free vortex shows discrete bound states with a ZBCP (Fig. 6(b)). To map out the spatial distribution, \(dI/dV\) mapping is performed around the vortex at different energies (Figs. 6(c)-6(m)). There are several remarkable features in these maps: (1) the low-energy vortex states generally display spatial oscillations with a wavelength of ∼1.8 nm, except the zero-energy mode [Fig. 6(c)]; (2) as \(\vert E \vert \) increases, the region with the highest LDOS gradually expands and eventually became “ring-like”, while the distribution is different for +E and −E states. (3) The LDOS shows anisotropic distribution with high-intensity “tails” along the Fe-Fe direction.

Figure 6
figure 6

(a) Averaged superconducting gap spectrum taken on clean area of FeSe-terminated surface. (b) Summed \(dI/dV\) spectra at the vortex core (inset image). Red curve is the multi-Gaussian fit. Numbered arrows near the peaks indicate the energy position where the \(dI/dV\) maps in panels (c)–(k) are taken. (c)–(m) High spatial resolution \(dI/dV\) maps of the vortex in panel (b) [52]

Full size image

A quantitative analysis on the vortex states distribution is shown in Fig. 7. The oscillations of \(E_{1}\) an \(E_{-1}\) are clearly out of phase, as seen in their line profile (Fig. 7(d)) and “phase referenced” FFT image (Fig. 7(b)). Specifically, \(E_{1}\) has a local maximum at the core center, while \(E_{-1}\) has a local minimum. Such behavior is well expected for an s-wave superconductor with an electronlike Fermi pocket, as calculated by Ref. [6]. The oscillation period of \(E_{1}\) and \(E_{-1}\) state are consistent with the bulk Fermi wavelength of (Li, Fe)OHFeSe. This indicates they and most high level state are from the bulk band of (Li, Fe)OHFeSe.

Figure 7
figure 7

Spatial distributions of the vortex states. (a) FFT of the \(dI/dV\) maps of \(E_{-1}\) state. (b) “Phase referenced” FFT of the \(E_{\pm 1}\) states (focused on center ring). (c) FFT line profiles along the Γ-M direction. (d) Line profiles of the \(dI/dV\) maps along the Fe-Fe direction. (e) Color plot of the symmetrized \(dI/dV\) line profile. (f) Calculations of the vortex states distribution under \(s_{++}\), \(s_{\pm} \), and nodeless d-wave pairing of the bulk state of (Li,Fe)OHFeSe (line cut across the vortex center). (g) Simulations of the zero-energy vortex mode from the topological surface state, and conventional \(\mu =\pm 1/2\) CdGM states [52]

Full size image

For the zero-energy mode \(E_{0}\), the maximum intensity is at \(d = 0\) [Fig. 6(c)], and it decays exponentially with a length scale of ∼3.2 nm [the fit in Fig. 7(d)]. Since theoretical works show that the vortex states of a full gap superconductors shall always have \(k_{F}\) oscillation, regardless of the pairing symmetry [6, 7, 64], the absence of oscillation for \(E_{0}\) mode implies it originates from a band other than the bulk ones. ARPES measurements have indicated that (Li, Fe)OHFeSe system host a topological surface state in the bulk band gap with a small \(k_{F}\) about \(0.028~\mathring{\mathrm{A}}^{-1}\). It is rational to assign \(E_{0}\) to the topological surface state, as its wave length \(\lambda _{F}\) (∼22 nm) is much larger than the decay length, thus the corresponding oscillation is unlikely to be observed. Figure 7(g) shows the analytical solution of the conventional CdGM states and zero energy mode, assuming that they come from aforementioned bulk band and the surface state with different \(k_{F}\), respectively. They well reproduced the main experimental features.

Moreover, in Ref. [52] the vortex states of (Li, Fe)OHFeSe with different pairing symmetries are also simulated [Fig. 7(f)]. The observed behavior of vortex states is more consistent with the \(s_{++}\) pairing, while the features expected by other pairing symmetries such as bonding-antibonding \(s_{\pm} \) and d-wave pairing [65, 66] are not observed. Overall, the above results indicate the nonzero energy states originate from bulk band; while the zero-energy mode is likely from the topological surface state. Therefore, the spatial behavior can help to distinguish the MZM from other trivial in-gap states, and it may be applied to other possible topological superconducting systems. The spatial property of vortex states can also help to understand the pairing nature of host superconductors.

5 The vortex state of single-layer FeSe/SrTiO3

Single-layer FeSe/SrTiO3 film is also a heavy electron-doped FeSe-based superconductor [67], but its electronic structure is different from (Li, Fe)OHFeSe. It is a rather two-dimensional system, and there is no interlayer coupling which exist in bulk materials. Previous band calculations have shown there is no topological band inversion near the Fermi level [32], and there are only two electron pockets on each M point in the Brillouin zone (BZ) [68, 69]. Therefore, it will be instructive to compare the behaviors of vortex states in FeSe/SrTiO3 and (Li,Fe)OHFeSe.

In addition, single-layer FeSe/SrTiO3 possibly has the highest \(T_{C}\) (≥65 K) or gap close temperature of all the Fe-based superconductors [67–69]. Its superconductivity enhancement mechanism is also of fundamental importance. In order to reveal such mechanism, an important aspect is to determine the superconducting pairing symmetry. In 2015, Fan et al. [70] used impurity effect and quasiparticle interference (QPI) experiments to show that single-layer FeSe/SrTiO3 has plain s-wave pairing. Recently, theoretical works show that nodeless d-wave pairing is also possible if finite SOC is present in the system [71], which was subsequently supported by some STM experiments [72, 73]. However, it should be pointed out that so far experiments to test the pairing symmetry of single-layer FeSe are all based on impurity-related effects, which depend on the details of impurities such as scattering potential [74] and whether the impurities are magnetic or not [75]. However, these parameters are often difficult to be determined directly. The behavior of vortex state is also highly related to pairing symmetry [2–4, 76], and they are induced by magnetic field which is independent of impurities. Therefore, studying the vortex state could provide more clear information on superconducting pairing.

Single-layer FeSe film was grown on Nb-doped SrTiO3 (001) substrate by MBE and post annealed to improve crystallinity. The typical topography is shown in Fig. 8(a). Figure 8(d) shows a typical U-shaped superconducting gap with a flat bottom and two pairs of coherence peaks. Such gap structure can be accounted by a single band anisotropy gap function that obtained by ARPES experiment in Ref. [77]:

$$ \Delta _{k} = \Delta _{0} -A\cos ( 2 \theta _{k} ) +B\cos ( 4 \theta _{k} ) $$
Figure 8
figure 8

(a) STM image of FeSe/SrTiO3 film; (b) zero-bias \(dI/dV\) mapping at \(B = 10\text{ T}\) which show vortex cores. (c) Sketch of the gap distribution on the electron pocket at M. \(\Delta _{2}\), \(\Delta _{1}\) and \(\Delta _{\mathrm{min}}\) correspond to the two local gap maxima and the gap minima, respectively. (d) typical gap spectrum (blue curve) of 1 ML FeSe and the fitted gap is shown in red curve; (e), (f) \(dI/dV\) spectra taken across vortex core. (g) Color plot of the spectra in (f) [51]

Full size image

As shown in Fig. 8(c), this gap function produces two local gap maxima at \(\Delta _{2} = \Delta _{0} +A+B\), and \(\Delta _{1} = \Delta _{0} -A+B\), which generate two pairs of coherence peaks in \(dI/dV\), while the average gap over the Fermi surface is \(\Delta _{0}\). The red curve in Fig. 8(d) is the fitted result of the superconducting gap.

After applying a perpendicular magnetic field, the vortices can be observed in zero-bias \(dI/dV\) mapping, as shown in Fig. 8(b). Some of the vortices are pinned by defects on the surface. In most cases, in-gap states are induced near the surface defects [51]. In order to avoid the influence of impurity, only unpinned vortices are studied (the region where they appear shows clean superconducting gap at zero field). Figure 8(e) and 8(f) show the \(dI/dV\) line cut taken across free vortices, with clear multiple discrete peaks near the core center, but there is no ZBCP. Figure 8(g) is the color plot of the spectra in Fig. 8(f). Generally, these nonzero energy states are symmetrically distributed and equally spaced with respect to \(E_{F}\), and their peak positions remain unchanged within a certain range away from vortex center. Far away from the vortex core, these low-energy discrete peaks gradually vanish, while a pair of broader peaks appear at higher energies.

Through quantitative peak position fitting, it is found that the ratio of the peak energies to their spacing δE are all close to half-integer values (\(E /\delta E=\pm 1/2\), \(\pm 3/2\), or \(\pm 5/2\)), which is expected for the CdGM states in s-wave superconductors [2, 6]. The high-energy shifting peaks are actually closely packed states, as the spacing of CdGM states decreases at high energy, which is similar to the behavior of vortex states in NbSe2 [5, 28]. The energy spacing δE varies for different vortices, which is due to local variation of superconducting gap. The energy spacing observed at different vortices can be reasonably accounted by \(( \Delta _{0} )^{2} / E_{F}\). Therefore, a single anisotropic superconducting gap can explain both the superconducting double-gapped spectrum and the discrete CdGM states.

Furthermore, Ref. [51] also simulated the vortex states of single-layer FeSe under different pairing symmetries, including the s-wave and nodeless d-wave pairing [71], as shown in Figs. 9 (c)-(d). The simulation is based on a two-band \(k.p\) model to describe low-energy superconducting quasiparticles [71]. For s-wave pairing [Fig. 9(c)], the simulated vortex states are symmetrically distributed around \(E_{F}\) with equal spacing, which is typical CdGM states. As approaching the vortex center, the intensities of the low energy states increase and show a certain particle-hole asymmetry [6], which is qualitatively agreed with the experimental data. However, the results of nodeless d-wave pairing display two sets of CdGM states [Fig. 9(d)] (which is due to SOC induced band hybridization at M). However, such behavior is not evidenced in the data. In addition, for nodeless d-wave pairing, zero-energy Andreev bound states are expected to exist on the {[110]} oriented boundaries [78] (due to the π-phase shift in the reflection of quasiparticles), while such boundary states should be absent for conventional s-wave superconductors. The measurement on the boundary along [110]Fe direction is shown in Figs. 9(e)-(f), including the boundaries between 2 ML FeSe and 1 ML FeSe [Fig. 9(e)] and the step edge of 1 ML FeSe [Fig. 9(f)]. In general, no zero-energy are observed on these [110]-oriented boundaries, which disfavors nodeless d-wave, but consistent with the s-wave pairing. Therefore, the above studies of CdGM states and boundary states provide independent clues for the pairing mechanism of single-layer FeSe/SrTiO3 films.

Figure 9
figure 9

(a), (b) Low energy spectra of two vortex cores. Red curves are multiple Gaussian-peak fit. (c), (d) Calculated vortex states under s-wave pairing (c) without SOC, and nodeless d-wave pairing (d) with \(\lambda = 0.02\text{t}\) at different distance to the core center; (e), (f) \(dI/dV\) spectra taken along the arrow in the inset panel. Inset: STM images of a boundary between 2 ML/1 ML FeSe (e) and atomic step edge of 1 ML FeSe (f) [51]

Full size image

As discussed in Sect. 2, the interlayer coupling in (Li,Fe)OHFeSe leads to band inversion and topological surface states, which can eventually lead to MZM in the vortex core. For the single-layer FeSe film, interlayer coupling is certainly absent, the absence of ZBCP in the vortex core and Andreev bound states at boundaries indicate it is a s-wave topological trivial system. Therefore, interlayer coupling which induces band inversion is an important prerequisite for realizing topological superconductivity in iron-based superconductors.

6 Summary and outlook

The searching of MZMs that suitable for topological quantum computation is a hot topic in condensed matter physics. One important direction is to find MZMs in the vortex core of topological superconductors. This review focuses on the study of FeSe based high-TC superconductors (Li, Fe)OHFeSe and single-layer FeSe/SrTiO3 by high-resolution STM. Clear ZBCP and its quantized conductance were observed in the free vortex cores of (Li0.84Fe0.16)OHFeSe; while only conventional CdGM states were found in the vortex of single-layer FeSe/SrTiO3. The spatial distribution of (Li0.84Fe0.16)OHFeSe suggest the zero-energy mode is from the topological surface state, which is different from other trivial bound states. These studies provide a potential platform for further exploring MZMs, and also helps to clarify the origin of MZM in iron-based superconductors.

At present, MZMs have been found in various iron-based superconductors, such as Fe(Te, Se) [10, 37, 38], (Li, Fe)OHFeSe [49, 50], CaKFe4As4 [79] and LiFeAs [80, 81]. It was also reported in superconducting topological materials such as WS2 [82]. Besides, other kinds of Majorana quasiparticles are detected on the hinge [83, 84], domain wall [85] and atomic line defects [86] of Fe(Te, Se) system. However, although strong signatures of MZMs have been successfully observed, their physical properties still need to be further studied, such as the spin polarization of MZM [7, 48] and non-abelian statistics [17, 18]. Furthermore, a controllable manipulation of these Majorana states is still highly desired for eventually achieving topological qubits.