1 Band folding in graphene/hBN moiré superlattice

The properties of electrons in solids are crucial for both fundamental research and applications. In condensed matter physics, the electronic properties of solids can be mainly described by band theory, which describes the eigenstates of electrons in a solid as energy bands [1]. Thus, identifying the band structures may yield an explanation for a wide range of electronic properties of materials, such as the effective mass and Fermi velocity of electrons, and help distinguish between metals and insulators according to the electrons’ filling of the energy bands. Band theory is therefore considered the basis of the modern semiconductor industry and is one of the most crucial theories in condensed matter physics.

Generally, the most efficient method by which to control the electronic properties of a material is to modify its lattice structure. To demonstrate the effect of band engineering from the lattice, we considered a 1D system (the simplest case) as an example. As shown in Fig. 1, for 1D free electrons, the energy dispersion relationship is parabolic: \(E_{k} \propto k^{2}\). When a periodic potential from the atomic lattice is applied (lattice constant a), the pristine parabolic energy band is folded into the first Brillouin zone (BZ) with a bandgap opening between the valence and conduction bands at the first BZ boundary \(k=\pm {\pi} / {a}\). To further modify the energy bands of this 1D atomic chain, a superlattice potential with a superlattice constant of na (\(n > 1\)) can be applied. As a result, the valence and conduction bands are further folded into a superlattice mini BZ (mBZ), and a series of superlattice minibands with a reduced wave vector \(k= {\pm \pi} / {\mathit{na}}\) are formed.

Figure 1
figure 1

Band folding due to the periodic potentials in 1D. The band structures of the 1D free electrons, electrons under atomic lattice modulation, and electrons under superlattice modulation are depicted from left to right

Full size image

Regarded as typical representatives of band theory in two dimensions, graphene and hexagonal boron nitride (hBN) exhibit distinguishable band structures (Fig. 2, left). Because of the similar honeycomb lattice with two sublattices in one unit cell, the valence and conduction band edges are located at K and K′ points in the hexagonal BZ [2]. The two sublattices have identical carbon atoms in graphene and different boron and nitrogen atoms in hBN, which are responsible for the gapless and gapped band structures of graphene and hBN, respectively (Fig. 2, middle).

Figure 2
figure 2

Graphene, hBN, and graphene/hBN moiré superlattices. Left panel shows the graphene and hBN lattices. The dashed diamond represents the unit cell. In the middle panel, the black solid and blue dashed hexagons represent the first BZs of graphene and hBN, respectively. The red small hexagon represents the mBZ of the moiré superlattice. The panel also depicts the schematic band structures of graphene, hBN, and graphene/hBN moiré superlattices. The right panel shows a schematic of the graphene/hBN moiré superlattice at zero twisting. The red diamond represents the moiré unit cell with the largest moiré period (\(L_{\mathrm{m}} = 15\) nm)

Full size image

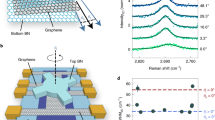
Both the gapless and the gapped band structures of graphene and hBN indicate the inversion symmetry between the two sublattices. To open a bandgap in graphene, the inversion symmetry must be broken between two identical carbon atoms in the unit cell. However, modifying the sublattices is difficult because this requires precise modifications at the atomic length scale. However, with the technical advances made in the understanding of 2D materials, such modifications can be simply realized by placing graphene on top of hBN through mechanical transfer [3] or direct growth [4]. Because of the different potentials of boron and nitrogen atoms acting on two carbon atoms in the unit cell [5], a bandgap of 100–300 K at the charge neutral point (CNP) was experimentally observed in aligned graphene/hBN (twisted angle \(\theta \sim 0\)). These results were obtained using various techniques, including electrical transport (Fig. 3(a)) [6], optical spectroscopy (Fig. 3(b)) [7], and angle-resolved photoluminescence spectroscopy (ARPES) [8].

Figure 3
figure 3

Experimental results indicating bandgap opening and band folding in graphene/hBN moiré superlattices. (a) Gap size at the CNP of graphene/hBN with different moiré periods extracted from transport measurements. The inset shows the Arrhenius plot of temperature-dependent conductance. (b) Optical transition energy between the zeroth Landau level on the hole side and the first Landau level on the electron side (T1 transition) in different magnetic fields. The 38 meV intercept in the zero magnetic field represents the gap at the CNP of graphene/hBN. (c) Graphene/hBN surface topography measured using scanning tunneling microscopy (STM) at four graphene/hBN locations with different twisting angles. (d) dI/dV curves of two moiré wavelengths in graphene/hBN, 9.0 nm (black) and 13.4 nm (red), measured by STM. The dips in the dI/dV curves marked by the arrows represent fully filled points (FFPs). (e) Energy dispersion of graphene/hBN measured by ARPES. The original Dirac cone and replicas are indicated by pink and green arrows, respectively. (f) Longitudinal resistance (black) and Hall resistance (red) as a function of gate voltage for a graphene/hBN device. The resistance peak near the zero gate corresponds to a CNP, and the two satellite peaks correspond to FFPs on the electron and hole sides. The sign changes of Hall resistance at the CNP and FFPs indicate the type change of charge carriers from holes to electrons. (g) Hofstadter’s butterfly represented in a Landau fan diagram indicating longitudinal resistance (left) and Hall resistance (right). Panels (a) and (b) are adapted from [6], panel (c) is adapted from [9], panel (d) is adapted from [10], panel (e) is adapted from [8], and panels (f) and (g) are adapted from [11]

Full size image

Given the lattice structure of aligned graphene/hBN on a large length scale, because of the tiny lattice mismatch of ∼2% between graphene and hBN, a moiré pattern with a substantially large period depending on the twisting angle is formed. As shown in the right panel of Fig. 2, when the twisting angle is \(\theta = 0\), the largest period is \(L_{\mathrm{m}} = 15\) nm. The moiré pattern was directly observed using STM (Fig. 3(c)), indicating that this pattern functioned as a superlattice that modified the electronic states of graphene [9, 10, 13].

The moiré superlattice in real space corresponds to an mBZ in the k space, in which the pristine bands of graphene are folded and form a series of minibands, as depicted in Fig. 2. A second Dirac point, or more generally an FFP, located between the first and second minibands on the valence or conduction side is a prominent signature of band folding [14, 15] and was directly observed as a density-of-state minimum in STM (Fig. 3(d)) [10] and ARPES (Fig. 3(e)) [8] measurements. As shown in Fig. 3(f), electrical transport measurements confirmed the existence of FFPs through satellite resistance peaks and Hall sign changes when graphene/hBN was doped into four electrons or holes per moiré unit cell (considering fourfold degeneracy in graphene from spin and valley) [4, 6, 11, 16, 17]. As shown in Fig. 3(g), when the moiré superlattice period is comparable with the electron magnetic length in perpendicular magnetic fields, Hofstadter butterfly was experimentally observed for the first time in a solid [6, 11, 16].

2 General approach for designing a 2D correlated system

For a classical 2D electron system with parabolic energy dispersion, the e–e interaction U and the bandwidth W can be estimated as follows:

$$\begin{aligned} &U \approx \frac{e^{2}}{4\pi \varepsilon L}, \end{aligned}$$
(1)
$$\begin{aligned} &W \approx \frac{\hslash ^{2} k^{2}}{2 m_{e}^{*}} \approx \frac{\hslash ^{2} \pi ^{2}}{2 m_{e}^{*} L^{2}}, \end{aligned}$$
(2)

Here, we assume that one electron exists per unit cell, ε is the effective dielectric constant of the dielectric environment, L is the lattice constant, e is the electron charge, ℏ is the reduced Plank constant, k is the wave vector, and \(m_{e}^{*}\) is the electron effective mass. The correlation strength can be estimated using \({U} / {W}\), and it linearly scales with \(m_{e}^{*} L\). To design a correlated 2D system (\({U} / {W} >1\)), either or both L and \(m_{e}^{*}\) must be sufficiently increased.

To meet the design criteria of large \(m_{e}^{*} L\), moiré superlattices are considered as a unique playground that provides huge L and a large material library for selecting proper 2D materials with large \(m_{e}^{*}\). Following this general approach, strong correlations were realized in ABC trilayer graphene on hBN (ABC-TLG/hBN) moiré superlattices, in which L increased ∼60-fold—from 2.46 Å in graphene to 15 nm in graphene/hBN—and \(m_{e}^{*}\) increased from zero in monolayer graphene to \(\sim 0.1 m_{0}\) in ABC-TLG (\(m_{0}\) is the rest mass of an electron). Tunable Mott insulators [12], superconductivity [18], ferromagnetism [19, 20], and Chern insulators [19] have been observed in ABC-TLG/hBN moiré superlattices (Fig. 4). Following the same approach, another suitable system consisting of twisted transition-metal dichalcogenide (TMD) bilayers, which exhibit even stronger correlations than those of ABC-TLG because of their larger \(m_{e}^{*} \approx 0.5\ m_{0}\) and similar moiré period L≈ 10 nm, was also realized shortly after ABC-TLG/hBN. Mott insulators [21, 22], Wigner crystals [21, 23, 24], stripe phases [25], and Chern insulators (quantized anomalous Hall) [26] have been observed in twisted TMD moiré systems.

Figure 4
figure 4

Experimental phase diagram of an ABC-TLG/hBN moiré superlattice. The nature of the Mott insulators and correlated resistive states at filling of −1 and −2 remains under debate

Full size image

From the other perspective, the crucial role of moiré superlattice for realizing strong correlations is efficiently narrowing the bandwidth due to band folding. According to Eq. (2), the bandwidth of the superlattice miniband is \(n^{2}\) times smaller than that of the pristine band. In the graphene/hBN moiré superlattice, the bandwidth decreases (\(60\times 60=\)) 3600-fold from band folding, indicating the capacity of the moiré superlattice to enhance the correlation strength of 2D materials.

3 Flatbands in ABC-TLG/hBN moiré superlattices

As shown in Fig. 5, trilayer graphene naturally has two stacking orders: ABA stacking (Bernal) and ABC stacking (rhombohedral). ABA-TLG has a monolayer-like linear band and a bilayer-like quadratic band, whereas ABC-TLG has a single band at low energy with a cubic dispersion relationship (\(E_{k} \propto k^{3}\)). Because of the unique cubic band, the band edge close to zero energy is quite flat and has a relatively large effective mass (\({\sim} 0.1 m_{0}\)) in ABC-TLG [27–31]. This flatband edge produces strong electron correlations and spontaneously broken symmetry states in pristine ABC-TLG [32–34].

Figure 5
figure 5

ABA- and ABC-stacked trilayer graphene. (a), (b) Top view of the lattice structures of trilayer graphene with ABA and ABC stacking orders. (c), (d) Perspective view of the lattice structures of ABA-TLG and ABC-TLG. The unit cells of ABA-TLG and ABC-TLG are marked by dark atoms and red dashed lines. (e), (f) Band structures of ABA-TLG and ABC-TLG calculated using a tight binding model

Full size image

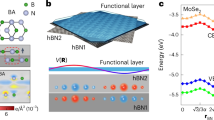
When ABC-TLG is placed on hBN in the presence of a moiré superlattice, the low-energy bands of bare ABC-TLG are folded into an mBZ, as shown in Fig. 6(a), in which only zone folding is considered [12]. Given the interaction between ABC-TLG and hBN, which is considered a periodic effective potential acting on the graphene layer in contact with aligned hBN, with the bottom layer of ABC-TLG taken as an example, the moiré pattern modifies the band structure features in the low-energy bands and introduces visible superlattice band features, as shown in Fig. 6(b), in which the band crossings are gapped in both the valence and conduction bands. As shown in Fig. 6(b), the narrowest miniband is the first mini valence band with a bandwidth of \(W \approx 20\text{ meV}\), which is comparable to the Coulomb energy \(U \approx 20\) meV estimated from Eq. (1), where \(L = 15\) nm and \(\varepsilon =5\) for hBN. Because the low-energy bands of ABC-TLG are captured by the hopping between the “A” atom in the top layer and the “B” atom in the bottom layer, the vertical electric field breaks the inversion symmetry of ABC-TLG and therefore opens a bandgap at the CNP. The calculated band structures at a potential difference of \(\Delta =20\text{ meV}\) (corresponding to the vertical electric field \(D \approx 0.4\) V/nm) between the top and bottom layers of ABC-TLG (Fig. 6(c)) clearly reveal that the moiré minibands in the mBZ are narrowed along with the bandgap opening. The first valence miniband is isolated from the other minibands and exhibits the narrowest bandwidth \(W \approx 13\) meV, which is nearly twice as small as the estimated Coulomb energy.

Figure 6
figure 6

Flatbands in ABC-TLG/hBN moiré superlattices. (a) Low-energy model of bare ABC-TLG in the mBZ of a superlattice where zone folding is observed. (b) The moiré pattern modifies the band structure features in the low-energy bands because of ABC-TLG and hBN interactions; it introduces visible superlattice band features at both the conduction and valence bands. (c) An external electric field is applied to bare ABC-TLG to open a bandgap proportional to an interlayer potential difference of \(2\Delta \approx 20\) meV. (d) When both a moiré pattern and interlayer potential differences are present, an isolated band with an excessively narrow bandwidth is formed, in which enhanced Coulomb correlation effects are expected. This figure is adapted from [12]

Full size image

4 Tunable correlations

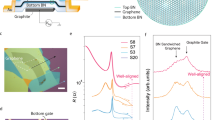
To experimentally obtain ABC-TLG/hBN moiré superlattice devices, the first step after exfoliation of TLG is to identify ABC-TLG. ABA-TLG is thermodynamically stable, whereas ABC-TLG is metastable but exists in Bernal stacked graphite as stacking fault domains [35, 36]. However, the ABC domains are quite stable in bulk graphite and in exfoliated flakes on \(\mathrm{SiO} _{2}\)/Si substrates, and they survive even after high-temperature annealing at 800–1000° C [37–39]. These ABC domains can be identified using Raman spectroscopy [39], scanning near-field optical microscopy (SNOM) [40], STM [41], and other scanning probe techniques [42, 43]. Among these different characterization techniques, SNOM, which combines the energy resolution of infrared light with the spatial resolution of atomic force microscopy (AFM), is an effective method for searching for ABC domains among exfoliated TLG flakes. Figure 7(b) shows a typical SNOM image of a TLG flake with mixed domains, in which the contrast of ABA-TLG and ABC-TLG originates from different optical responses of electrical dipoles of two stacking orders. Although ABC-TLG has a metastable phase, the experimental statistical probability of having an ABC domain in a TLG flake exfoliated from Kish or natural graphite is ∼20%.

Figure 7
figure 7

ABC-TLG/hBN dual-gate device fabrication process. (a) Optical image of an exfoliated trilayer graphene flake on a \(\mathrm{SiO} _{2}\)/Si substrate. (b) SNOM image of TLG. Areas with different contrast levels in TLG correspond to ABA and ABC domains. (c) Optical image of an isolated ABC-TLG domain after anodic-oxidation-assisted AFM cutting. (d) Optical image of an hBN/ABC-TLG/hBN heterostructure prepared using a dry transfer technique. (e) Optical image of the final dual-gate ABC-TLG/hBN device. (f) Cross-sectional view of the device shown in (e). (g), (h) Gate-dependent resistance of ABC-TLG and ABA-TLG at \(T = 50 K\). The colors correspond to different \(V_{\mathrm{b}}\) and \(V_{\mathrm{t}}\) values in (g) and (h), respectively. Panels (f), (g), and (h) are adapted from [12]

Full size image

Although obtaining ABC-TLG in exfoliated flakes is not difficult, ABC-TLG is not stable during the transfer process to hBN and during the subsequent device fabrication processes, such as metal evaporation [44]. This results in a low rate of success of sample preparation of ABC-TLG/hBN or even complicated van der Waals heterostructures. Isolating ABC from ABA domains by anodic oxidation AFM cutting [45] is an efficient process for stabilizing the ABC stacking order during transfer and subsequent fabrication processes (Fig. 7(c)) [12]. A dry transfer method can be used to encapsulate the isolated ABC-TLG by two hBN films (Fig. 7(d)) [46], followed by a standard device fabrication process to obtain a dual-gate device geometry (Figs. 7(e) and 7(f)). After device fabrication, transport measurement near liquid nitrogen temperatures can be conducted to identify the stacking order of the final device. As shown in Figs. 7(g) and 7(h), a bandgap was observed at the CNP in ABC-TLG when a vertical electric field was applied, but no bandgap was observed for ABA-TLG [12, 29].

A dual-gate geometry is crucial for realizing strong correlations because of its ability to individually tune the doping n and vertical electric field D, which helps tune the moiré bandwidth, as shown in Fig. 6. In the absence of a vertical electric field, when resistance was measured as a function of doping, as shown in Fig. 8(a), resistance peaks were observed at the CNP (\(n = 0\)) and FFPs of the first miniband (\(n = \pm 4 n_{0}\)). A broad but weak resistance peak was also identified between the CNP and FFPs on the hole side, which has not been observed in monolayer or bilayer graphene/hBN moiré superlattices, suggesting the existence of certain correlations given the estimated correlation strength (U/\(W \approx 1\); Fig. 6(b)).

Figure 8
figure 8

Transport measurement of tunable correlations in ABC-TLG/hBN. (a), (b) Resistance as a function of doping in the unit of miniband filling, n/\(n_{0}\), where \(n_{0}\) corresponds to one electron per moiré unit cell, at \(D = 0\) and 0.4 V/nm. (c) Color plot of resistance as functions of doping and electric field

Full size image

As illustrated in Fig. 6(d), when a vertical electric field D is applied, the bandwidth decreases, and therefore, the correlation strength increases in the ABC-TLG/hBN moiré superlattice. When resistance was measured as a function of doping at \(D = 0.4 V/\)nm (Fig. 8(b)), in addition to the FFP peaks at n/\(n_{0} = \pm \)4 and the CNP peak, which was insulating because of the bandgap opening, two prominent resistance peaks emerged at n/\(n_{0} = -1\) and −2, corresponding to one and two holes per moiré unit cell, respectively. Figure 8(c) shows a complete phase diagram represented by a 2D color plot of resistance as functions of n and D obtained by continuously tuning n and D. The diagram clearly depicts the evolution of resistance peaks at n/\(n_{0} = -1\) and −2 with the electric field. The absence of both peaks with weak correlations and their emergence with strong correlations, combined with the integer filling of the moiré unit cell, strongly suggested Mott insulating states [47].

ABC-TLG/hBN has two asymmetries: an electron–hole asymmetry and a vertical electric field asymmetry. The correlated states at n/\(n_{0} = -1\) and −2 are prominent only on the hole doping side and the positive D side. The electron–hole asymmetry can be clearly identified from the calculated band structures (Fig. 6(d)). Compared with the first conduction miniband, the first valence miniband is narrower and is isolated from remote minibands, and therefore, it demonstrates stronger correlations. The D asymmetry arises from the existence of moiré between ABC-TLG and only one side of the hBN layers (e.g., bottom hBN in Fig. 8(c)).

In the following, we examine some of the related energy scales in ABC-TLG/hBN and magic-angle twisted bilayer graphene (MATBG), which also shows strong correlations phenomenon originating from moiré flatbands. As discussed earlier, the estimated Coulomb energy U in ABC-TLG/hBN is 20 meV, and the calculated bandwidth W in a vertical electric field reaches 13 meV. According to temperature-dependent transport measurements, the largest transport gap is 2 meV [12]. For MATBG, W is calculated as 12 and 2 meV for the conduction and valence minibands, respectively, and the transport gaps are stimated as 0.3 meV for the correlated insulating states on both sides [48]. In both systems, U and W are nearly one order of magnitude larger than the Mott/correlated gaps. In a twisted TMD system, such as in \(\mathrm{WSe} _{2}\)/\(\mathrm{WS} _{2}\), the measured Mott gap is 50 meV, and U is 100 meV, both larger than the bandwidth of 10 meV, which is generally assumed to be a Mott insulator [22]. Energy scales such as bandwidth, Coulomb energy, and correlated gaps in ABC-TLG/hBN, as well as other moiré systems, have been individually measured using spectroscopic techniques, such as scanning tunneling spectroscopy [49–52] and optical spectroscopy [53]. For ABC-TLG/hBN, Fourier transform infrared photocurrent spectroscopy has been used to directly measure absorption peaks emerging at 18 meV, indicating direct optical excitation across an emerging Mott gap at n/\(n_{0} = -2\), which is nearly one order of magnitude larger than the transport gap [53]. For MATBG, considering that the moiré comes from two graphene monolayers and therefore introduces complex reconstructions and strains in the graphene lattice, the experimental results of the insulating behaviors and correlated gaps at integer fillings are sample dependent [54, 55].

In the following, we also discuss the competition between two energy scales: correlation energy and Landau level energy. In MATBG, Landau levels develop from n/\(n_{0} = 0\), ±1, ±2, and ±3 [56–59] down to ∼1 T, which corresponds to a Landau level gap of 0.1–1.0 meV, depending on the g factor. In addition, the Coulomb energy U in MATBG is estimated to be within 10 meV, which is much larger than the Landau level gap. Therefore, Landau levels are not expected to emerge in such a strongly correlated electron system within small magnetic fields in a naive understanding. However, the situation for ABC-TLG/hBN is much different. Landau levels emerge at small D when the correlations are weak, but they disappear at large D when the correlations are strong [19]. This substantial difference between the behavior of MATBG and that of ABC-TLG/hBN suggests different symmetry breaking scenarios and different types of correlated states. It is likely that the correlated insulating states in ABC-TLG/hBN are Mott insulators, which are the same with, but in weaker correlated strength than twisted TMDs. While for MATBG, Mott was the first understanding, then charge density wave [60], Anderson insulator [61] and Kramers intervalley-coherent (K-IVC) insulator [62] were proposed. Recent scanning probe experiments found cascade of electronic transitions, distinct changes in the chemical potential right before integer fillings, and different Landau level degeneracies for different Hubbard subbands directly evince the phase transitions associated with flavor symmetry breaking due to Coulomb interactions and the Chern insulator phases of the correlated insulating states [63–66].

5 Superconductivity

It is often speculated that high-Tc superconductivity arises in a doped Mott insulator as described by the Hubbard model (Fig. 9(a)) [67, 69–71]. With correlated moiré systems considered as Mott insulator candidates, studying superconductivity in such systems has attracted much attention. So far, superconductivity has been observed in some graphene moiré systems, including magic-angle-bilayer or multilayer graphene [56, 72–76] and ABC-TLG [18, 68].

Figure 9
figure 9

Superconductivity in different systems. Phase diagrams of BSCCO (2212), a high-Tc cuprate superconductor (a), MATBG (b), ABC-TLG/hBN moiré superlattice (c), and high-quality ABC-TLG without moiré (d). Panel (a) is adapted from [67], panel (c) is adapted from [18], and panel (d) is adapted from [68]

Full size image

In MATBG, superconductivity has first been reported as two superconducting domes at electron- and hole-doped correlated insulating states at n/\(n_{0} = \pm2\) with the highest Tc value reaching ∼1.7 K [56]. This dome-shaped superconductivity is highly similar to that of cuprate high-Tc superconductors, and this similarity has prompted an increasing number of studies to investigate the origin of superconductivity in MATBG. Some experimental signatures of unconventional superconductivity have been identified, such as strong pairing for a small Fermi surface [56], a strange metal phase above Tc [77], a nematic order in the superconductivity phase [78], tunneling spectra due to a nodal superconductor, and a large tunneling gap that persists at temperatures higher than Tc and indicates a pseudogap phase [79]. Figure 9(b) depicts the superconductivity phase of MATBG obtained from the experimental results. Because of the similarities between the phase diagrams of MATBG and the cuprate superconductor, the superconductivity of MATBG was assumed to be interaction-driven unconventional superconductivity.

Some experimental results, on the other hand, have suggested a conventional mechanism of superconductivity in MATBG. For instance, superconducting domes occur across a wide range of moiré flatband fillings despite resistive peaks at n/\(n0 = 0\), ±1, and ±2 in MATBG devices with highly uniform twisting angles [57]. This is in contrast to the presence of a high-Tc superconducting dome at narrow doping ranges close to Mott state. Strong linear-in-temperature resistivity (strange metal) has also been observed in magic-angle and non-magic-angle TBG devices, contributing to electron–phonon-scattering-dominated processes rather than to e–e interactions [80, 81]. The superconductivity in the absence of a correlated insulating state or in the presence of a weakened correlated insulating state in TBG devices, including MATBG with a closed graphene screening layer, metallic non-magic-angle TBG stabilized by a WSe2 layer, and simple non-magic-angle TBG, supports a competing picture, in which the correlated insulating state and superconductivity arise from different mechanisms [82–84].

As shown in Figs. 9(c) and 9(d), superconductivity was observed in ABC-TLG with and without hBN moiré superlattices. Superconductivity signatures were also observed in the ABC-TLG/hBN moiré superlattice close to the n/\(n_{0} = -1\) Mott state in a large vertical electric field [18]. Tuning the vertical electric field at fixed doping allowed for continuously tuning ABC-TLG/hBN from a metal to a Mott state to a superconductor. For ABC-TLG without moiré, two superconducting regions were observed proximal to the isospin-symmetry-breaking transitions where the Fermi surface degeneracies change in ABC-TLG [68]. One superconducting phase (SC2) occurred in a similar doping and displacement field to that of ABC-TLG/hBN moiré superlattice, suggesting the same origin of superconductivity in both systems. Similar superconductivity close to the isospin-symmetry-breaking transition was also observed in Bernal bilayer graphene without moiré [85].

6 Tunable topology and Chern insulator

Historically, graphene plays a crucial role in topological physics in condensed matter. In 1988, long before its discovery, graphene lattice with complex hopping terms was used by Haldane in a toy model to realize the quantum Hall effect in the absence of Landau levels (known as the quantum anomalous Hall effect), which is regarded as the first direct demonstration of the intrinsic topological properties of a material [86]. In 2005, Kane and Mele envisioned a quantum spin Hall (QSH) insulator in graphene by considering spin orbit interaction [87].

From an experimental viewpoint, graphene has demonstrated attractive topological properties since its discovery. For instance, the discovery of the half-integer anomalous quantum Hall effect due to the Berry phase of π can be regarded as the first experimental discovery of topological phenomena in graphene [88, 89]. When a large in-plane magnetic field was applied to graphene, QSH helical edge transport was observed [90]. A topological valley current was detected using a nonlocal transport measurement in gapped bilayer graphene in a perpendicular electric field [91, 92]. Quantized valley edge transport at the AB/BA domain wall of bilayer graphene was observed and regarded as a topologically protected 1D chiral state [40]. The Hofstadter butterfly spectrum was achieved by assessing the Landau level fan diagram of graphene on hBN moiré superlattices [6, 11, 16].

Upon discovering correlated moiré superlattices, researchers predicted that correlated topological phenomena may emerge in MATBG and ABC-TLG/hBN, in which a nontrivial band topology coexists with a nearly flat moiré miniband [93–97]. Given that moiré exists only between ABC-TLG and hBN on one side (e.g., bottom hBN), when a vertical electric field is tuned from positive (upward) to zero and then to negative (downward), the bandgap at the CNP is first opened and then closed and then reopened. During the bandgap reopening stage at negative D, band reversion occurs, accompanied by a change in the topological order. According to calculations, the Chern number is nonzero for the mini valence band and zero for the conduction band in a negative electric field, and the Chern numbers of these two minibands switch at positive D (Fig. 10(a)).

Figure 10
figure 10

Tunable topology of ABC-TLG/hBN. (a) Calculated single-particle band structure of ABC-TLG/hBN in the K valley for the displacement fields \(D = 0.5\), 0, and −0.5 V/nm. At \(D = 0.5\) V/nm, a finite bandgap separates the conduction and valence bands. The highest energy valence miniband is topologically trivial with \(C = 0\). The bandgap closes at \(D = 0\) V/nm. At \(D = -0.5\) V/nm, the bands are inverted to generate a new bandgap. The highest energy valence miniband becomes topologically nontrivial with a finite Chern number. The minibands of the K′ valley are time-reversed pairs of the K valley minibands and have opposite Chern numbers. (b) Anomalous Hall effect of ABC-TLG/hBN at n/\(n_{0} = -1\) and \(D = -0.5\) V/nm. (c) Quantized anomalous Hall effect represented by quantized ρyx and vanishing ρxx in a small magnetic field, indicating a Chern number of \(C = 2\). (d) Noninteger filling anomalous Hall (NIFAH) effect at n/\(n_{0} = -2.3\). (e) NIFAH ferromagnetic hysteresis loops in a tilted magnetic field. (f) The NIFAH curves in (e) are plotted as a function of the component of the field perpendicular to the sample plane \(B_{\bot}\). Panels (a), (d), (e), and (f) are adapted from [20], and panels (b) and (c) are adapted from [19]

Full size image

Shortly after the aforementioned calculations, the gate tunable topology of ABC-TLG/hBN moiré was experimentally observed. As predicted in a previous study [93], no topological phenomenon was observed on the trivial side when \(D > 0\). However, when D was reversed to a negative value, large anomalous Hall resistivity was observed at n/\(n_{0} = -1\). This Hall resistivity exhibits ferromagnetic hysteresis as a function of a perpendicular magnetic field with an amplitude of 8 k Ω (Fig. 10(b)). When a magnetic field exceeding 0.4 T is applied, the Hall resistivity is well quantized at h/2\(e^{2}\), accompanied by zero longitudinal resistivity, confirming a topological Chern insulator with a Chern number \(C = 2\) (Fig. 10(c)). Although the Chern insulator and quantized anomalous Hall effect were observed in a small magnetic field, the topological order is the same as the state at a zero magnetic field, thereby differentiating this Chern insulator from traditional quantum Hall insulators [19].

The observation of the Chern insulator demonstrates spontaneous time-reversal symmetry breaking in ABC-TLG/hBN because of strong e–e interactions. Although nontrivial Chern bands are predicted, opposite valleys (i.e., K and K′) exhibit opposite Chern numbers. No ferromagnetism or anomalous Hall effect could exist if the Fermi level passes through two degenerated valleys. The e–e interactions results in an energy difference between the valleys and opens a correlated gap at the filling of n/\(n_{0} = -1\), with the valley polarized (K valley) first Hubbard band being filled. Further measurements at higher filling at n/\(n_{0} = -2\) revealed no ferromagnetism, which is understood from the filling of the second Hubbard band with an opposite valley K′ and an opposite Chern number. A NIFAH effect was also observed near the filling of n/\(n_{0} = -2.3\) in ABC-TLG/hBN. The ferromagnetic response to the external field is strongly anisotropic with coercive field scaling with the out-of-plane component of the external magnetic field, indicating that the ferromagnetism is likely dominated by the orbital magnetic moment of the carriers.

Chern insulators and quantized anomalous Hall effects have also been observed in other moiré flatband systems, such as in MATBG aligned with hBN at \(C = 1\) [98], in twisted monolayers on bilayer graphene at \(C = 2\) [99, 100], and in twisted TMD moiré at \(C = 1\) [26]. In some moiré systems, magnetism is even switchable through electrical control; it can be switched from positive to negative by applying a dc current in MATBG [101] or by applying electric gating in twisted monolayer/bilayer graphene [99, 100], indicating that electrical-switchable magnetization can be understood from the orbital nature. Orbital magnetization is generated by the charge current of Bloch electrons with large orbital magnetic moments because of the large Berry curvatures of the flatbands [102]. However, electrical switching has not been reported in ABC-TLG/hBN or twisted TMD moiré.

7 Conclusions

The ability to achieve strong correlations in ABC-TLG/hBN and other moiré superlattices takes full advantages of the high tunability of 2D materials, including tuning the layer numbers, stacking orders, doping, vertical electric field, and twisted sequences or angles of van der Waals heterostructures. Compared with strongly correlated crystalline materials with hopping and localization in atomic length scales and electron-volt correlation energy scales, moiré flatband systems have a length scale of 10 nm and a millielectron-volt energy scale. The unique length and energy scales make the moiré superlattices difficult for potential applications, but suitable for fundamental studies because the scales are accessible and tunable in experimental studies. Many intriguing topics remain to be investigated in moiré flatband systems, such as the ground states at integer fillings, the mechanism of superconductivity, and high-temperature quantum anomalous Hall effect. However, to conduct precise systematic experimental studies in this field, higher sample quality and more complicated device structures are required. Novel techniques of sample preparation are also strongly needed, including more controllable twisting angles, higher efficiency in maintaining stacking orders, and direct growth methods.