Introduction

Electrospray describes the process by which a strong electric field is used to extract droplets or ions from a conductive liquid meniscus and accelerate them into a plume [1,2,3]. Electrosprays have found a variety of uses, such as ink-jet [4, 5] and 3D printers [6, 7]; drug delivery systems [8]; automotive [9], agricultural [10], cleaning [11,12,13], and fire-fighting sprays [14,15,16]; powder production [17,18,19]; mass spectrometry [20,21,22,23]; focused ion beam (FIB) micromachining or ion etching [24, 25]; and as thrusters for spacecraft electric propulsion [26,27,28,29,30]. The low thrust-noise (\(\sim\)100 nN \(\cdot {}\) Hz\(^{-\frac{1}{2}}\)) and high thrust-precision (\(\sim\)nN – \(\upmu\)N) of electrospray thrusters are of interest for upcoming missions, such as the Laser Interferometer Space Antenna (LISA) and the Habitable Exoplanet Observatory (HabEx) [31,32,33,34,35].

Electrospray thrust is achieved by ions and/or droplets extracted from a source of high conductivity liquid (capillary, needle, porous structure, etc) and accelerated by a high voltage through an electrode a small distance away. The first electrospray thruster to successfully operate in space was the Colloid MicroNewton Thruster (CMNT) developed by Busek Co., Inc. and NASA Jet Propulsion Laboratory (JPL), as part of the Space Technology 7 - Disturbance Reduction System (ST7-DRS) [31] flown on the LISA Pathfinder mission [36]. While 7 out of 8 of the deployed thrusters demonstrated thruster lifetimes in excess of 2400 hr [37], future missions require an order of magnitude more lifetime to be successful [38].

Impingement of electrospray electrodes has been identified as the source of many critical life-limiting phenomena for electrospray thrusters [36, 39, 40], and is governed by the mass flux of the plume at wide angles that may subtend the electrodes. The ability of previous efforts to predict mass flux from impinging current have been hindered by polydispersity in the plume [41,42,43,44,45]. Furthermore, measurements of electrode impingement current are particularly susceptible to uncertainty from secondary species emission (SSE) from impinged surfaces [46,47,48,49]. Wide-trajecting massive species also constitute a thrust inefficiency, making their quantification even more desirable.

The mass flux distribution of a capillary electrospray system (of an accelerator-less CMNT design [37]) was previously measured with a water-cooled Quartz Crystal Microbalance (QCM), and estimates of device lifetime were proposed [39, 45]. While mass flux profiles of the plume were found to be super-Gaussian in form [45], the data at the highest angles (relevant for electrode impingement) were below the QCM device resolution of 10 pg cm\(^{-2}\) s\(^{-1}\).

As electrode impingement has been identified as the primary failure mechanism of an electrospray thruster [37, 39, 40], calculating the rate of impingement can bound the likelihood of a number of life-limiting phenomena [45], and inform the design of the thruster to mitigate electrode-impingement. The amount of mass accumulating on an electrode from overspray \(\left( \dot{M}_{impinge}\right)\) can be calculated by Eq. 1:

$$\begin{aligned} \dot{M}_{impinge}=2\pi r^2\int ^{\frac{\pi }{2}}_{\theta _{elec}}{\dot{m}\left( \theta \right) \sin {\theta } \textrm{d}\theta }, \end{aligned}$$
(1)

where r is the radial distance to the mass flux detector, \(\dot{m}\left( \theta \right)\) is the measured mass flux, \(\theta\) is polar angle from the thrust axis, \(\theta _{elec}\) is the line-of-sight angle from the emitter to electrode aperture, and emission is assumed to be axisymmetric [50]. Note that the upper limit of the integral is \(\frac{\pi }{2}\) as we are only concerned with particles impinging the downstream electrodes, which for the CMNT are always downstream of the emitter; the upper limit may change depending on specific thruster geometry. Marrese-Reading et al. [51] suggest that an overspray mass loading rate (i.e. impinging mass flux) of 0.01 g yr\(^{-1}\) is a desirable target for CMNT-type thruster lifetime; an improvement in mass flux resolution is required to determine if the impinging mass flux for CMNT-type electrodes is within desired limits.

Collins et al. [39] and Parmar et al. [52] showed that with the previously-measured super-Gaussian form of mass flux and charge density, substantial tightening of the plume is expected when an accelerating voltage is applied, on the order of 10\(^{\circ }\). Accordingly, the anticipated mass flux at the accelerator electrode is substantially reduced by plume acceleration, such that extractor-impingement is considered a more-likely source of thruster failure than accelerator-impingement.

The objective of the present study is to provide high-resolution mass flux measurements at high plume angles, and provide a data-driven model for electrode mass impingement as a function of beam current. The presented analysis has the CMNT geometry in mind, but the methodology and concepts concluded are applicable to similar electrospray devices.

Experimental Setup

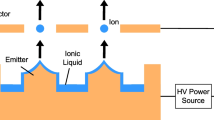
The Highly Optimizable Apparatus for Groundbreaking Investigations of Electrosprays (HOAGIE) facility at UCLA PSPL was developed to investigate various aspects of electrospray emission. A description of HOAGIE has been given previously [45, 53], and results presented herein extend the capability of HOAGIE to measure very low mass flux at high plume angles with a Thermoelectric Quartz Crystal Microbalance (TQCM) on an actuated armature. A schematic of the HOAGIE configuration used in the present study is shown in Fig. 1.

Fig. 1
figure 1

Schematic of HOAGIE with actuated TQCM. An electrospray is formed with EMI-Im propellant delivered from a pressure-over-fluid (POF) chamber to an emitter capillary held at high voltage relative to a grounded extractor plate. Emitter tip is viewed with a stereoscopic long distance microscope (LDM). TQCM is mounted on an actuated armature at a fixed radial distance from the emitter tip, and can be actuated from 30\(^{\circ }\) to 50\(^{\circ }\), measured by string potentiometer. Arrows indicate possible actuation

Full size image

Electrospray

The electrospray under investigation consists of a platinum capillary emitter and a stainless steel extractor plate, with part dimensions matching those of the CMNT in the ST7-DRS [37]. 1-ethyl-3-methylimidazolium bis(triflouromethylsulfonyl)imide (EMI-Im) was used as propellant to match CMNT conditions. Propellant was conditioned and vacuum dried to ensure minimal water content, in accordance with best practices for electrospray thruster operation [54]. To operate, a high voltage was applied to the emitter under vacuum, and the extractor was grounded; for all experiments reported herein, the input flow rate (and hence current) was varied, and the emitter was held at 1.6 kV, which was found to be the most stable voltage for the given system [50].

HOAGIE is operated without an accelerator in order to investigate species that would exist in the extractor-accelerator region; such plume species are a direct result of extraction processes and not conflated by acceleration effects that may obscure particle origins. The lack of an accelerator does not change the emitter-extractor voltage difference from that used during nominal thruster operation, so emitted species are expected to be representative. Operating without the accelerator has the added advantage of using lower total voltages for operation, and thus reducing secondary species emission (SSE) than can obfuscate measurements [49, 55]. Electrostatics are expected to provide the dominant forces in the post-extractor region [40, 56, 57], whereby simple models can accelerate the measured plume to predict performance and life in the presence of an accelerator [39, 52].

TQCM

Quartz Crystal Microbalances (QCM) have been used in a few instances to measure mass flux of electrospray thruster plumes [45, 58, 59], and are a vital tool in many areas of science and technology [60]. The microbalance operates by monitoring the resonant frequency of a quartz crystal; since quartz is piezoelectric, resonance can be stimulated and monitored with an appropriately oscillating voltage. As material is deposited on the quartz crystal, its resonant frequency changes as a function of mass. By monitoring the changing frequency, a measurement of mass flux is achieved via the Sauerbrey Eq. [61], if the frequency change is <5% of the initial frequency:

$$\begin{aligned} \frac{\textrm{d}m}{\textrm{d}t} = -\frac{\sqrt{\rho _q\mu _q}}{2f^2_0}\frac{\textrm{d}f}{\textrm{d}t}, \end{aligned}$$
(2)

where \(\frac{\textrm{d}m}{\textrm{d}t}\) is the mass flux, \(\rho _q\) is the density of the quartz crystal, \(\mu _q\) is the shear modulus of the quartz crystal, \(f_0\) is the initial resonant frequency, and \(\frac{\textrm{d}f}{\textrm{d}t}\) is the rate of change of the measured frequency.

Typical quartz crystal oscillations of QCM devices are on the order of a few MHz, with appropriate electronics required to drive and measure such oscillations. The thermoelectric QCM (TQCM) provides an orders-of-magnitude improvement in resolution by keeping the temperature of the crystal fixed, and using a second crystal for a reference frequency [62]. If the reference crystal is kept at the same temperature as the experiment crystal, and not exposed to mass impingement, a beat frequency of a few kHz can be generated by mixing the resonance frequencies of the loaded and unloaded crystals, which can be measured more accurately than the MHz order signal. A TQCM and associated controller from CrystalTek corp.Footnote 1 were used in the presented experiments. The exposed crystal was located facing the electrospray emission, and the beat frequency drift was recorded for up to 300 s, in order to reduce statistical noise in the measurement. It was found that reducing the TQCM crystal temperature below 15 \(^{\circ }\)C shifted the baseline frequency drift by up to 0.5 ng cm\(^{-2}\)s\(^{-1}\) at \(-40 ^{\circ }\)C, but did not change the relative frequency shift imposed by impinging electrospray mass flux by more than 2% compared to nominal operation at 20 \(^{\circ }\)C. At 15 \(^{\circ }\)C and above, the baseline frequency drift remained constant, so for all reported measurements, the TQCM was held at 20 \(^{\circ }\)C.

At an emitter-extractor voltage difference of 1.6 kV, Uchizono et al. [49] showed that electrosprayed species impinging on a surface are below the shock-desorption threshold. In keeping with this finding, Thuppul et al. [45] found that the integrated beam mass flux measured by a QCM for such conditions were consistent with the input flow rate. The same operating conditions were used for this study such that it can be assumed that only a small amount of propellant was lost from the TQCM surface.

As shown in Fig. 1, an actuated armature with one rotational degree of freedom was constructed to mount the TQCM; the mount pivoted on an axis coincident with the emitter tip, and could move from 30\(^{\circ }\) to 50\(^{\circ }\) with 0.1\(^{\circ }\) precision. The armature was actuated by an Arduino-controlled stepper-motor-driven linear stage, and its position monitored by string potentiometer. The rotation range was chosen to interrogate the high angle regions of the plume where detectable mass flux dropped below the noise floor of the QCM reported by Thuppul et al. [45], and to go beyond the line-of-sight angle of the extractor aperture where mass flux was expected to be zero. The TQCM was mounted (150 ± 5)mm from the emitter tip, and an actuated shutter installed in front of the TQCM.

Meniscus Imaging

The edge of the plume is of interest for examining possible electrode impingement, so the electrode location needs to be defined relative to the emission source as a function of operating conditions. During spray, a meniscus is formed at the emitter tip which grows with increasing flow rate (and hence current); assuming most emission is from the tip of the meniscus, growth of the meniscus changes the line-of-sight angle of the extractor (\(\theta _{ext}\)) relative to the fixed geometry of the thruster, per the inset of Fig. 3. \(\theta _{ext}(Q)\) (where Q is flow rate) is calculated from the meniscus height, h(Q), emitter distance, d, and extractor aperture diameter, \(D_{ext}\), as:

$$\begin{aligned} \theta _{ext}\left( Q\right) =\tan ^{-1}{\left( \frac{D_{ext}}{2\left( d-h\right) }\right) }. \end{aligned}$$
(3)

Equation 3 shows that as the height of the meniscus increases, \(\theta _{ext}(Q)\) increases, allowing wider plumes to not strike the electrode. As shown in Fig. 1, a microscope is focused on the emitter tip and meniscus, from which measurements of meniscus height were obtained. Figure 2 shows an example of the meniscus growth with flow rate during operation.

Fig. 2
figure 2

Evolution of the electrospray meniscus with beam current. Yellow lines show the increasing height (h) of the meniscus with increasing current

Full size image

Results

Over the range of currents reported herein, \(h\left( Q\right)\) was measured to change from 7.5% to 10.5% of the emitter-extractor spacing (d), meaning \(\theta _{ext}(Q)\) is expected to change by 2.3\(^{\circ }\) to 3.1\(^{\circ }\) from the nominal extractor line-of-sight (\(\theta _{ext,0}\)), as shown in Fig. 3.

Fig. 3
figure 3

Change in extractor line-of-sight angle as a function of beam current. A linear fit to the data is also shown for approximating \(\theta _{ext}(Q)\). Inset: How the presence of a meniscus changes the line-of-sight angle of the extractor \(\theta _{ext}\) as a function of flow rate, Q. As the meniscus increases, the height, h(Q), increases, \(\theta_{ext}\left( Q\right)\) increases, allowing wider plumes to not strike the electrode

Full size image

TQCM measurements of mass flux over a range of flow rates at (150 ± 5)mm from the emitter tip are shown in Fig. 4. The plume angle has been scaled relative to the appropriate \(\theta _{ext}(Q)\) for the given beam current. For the higher beam currents, which exhibit broader plume profiles, extractor electrode impingement eliminates flux beyond the extractor line of sight (i.e. for \(\frac{\theta }{\theta _{ext}\left( Q\right) }>1\)), resulting in measured flux reducing to the TQCM noise floor. The log scale plot shows that the noise floor of the TQCM in HOAGIE is \(\sim\)2 pg cm\(^{-2}\)s\(^{-1}\), representing a five-fold improvement in resolution over previous data [45]. For beam currents less than \(\sim\)600 nA, the mass flux drops below detectable levels at angles lower than \(\theta _{ext}\left( Q\right)\), indicating that at low enough beam currents there is no discernible mass flux to the extractor during steady state emission.

Fig. 4
figure 4

Mass flux reported by TQCM (150 ± 5)mm from emitter tip as a function of fractional line-of-sight angle. \(n=3\) super-Gaussian fits, per Eq. 4, are shown with dashed lines. No mass flux is detected beyond \({{\theta }/{\theta _{ext}\left( Q\right) }=1}\). Note, for currents <600 nA the mass flux drops below detectable levels before reaching \(\theta _{ext}\left( Q\right)\), while currents >600 nA have progressively more truncated plumes to maintain zero mass flux beyond \(\theta _{ext}\left( Q\right)\), due to extractor impingement

Full size image

Discussion

Thuppul et al. [45] proposed a super-Gaussian fit to parameterize mass flux profiles (\(\dot{m}(\theta )\)), with changes in flow rate typically having an \(n=3\) form, per Eq. 4:

$$\begin{aligned} \dot{m}(\theta ) = A\cdot \exp {\left\{ -\left( \frac{\theta ^2}{2\sigma ^2}\right) ^3\right\} }, \end{aligned}$$
(4)

where A is a scale factor for the super-Gaussian, \(\theta\) is polar angle, and \(\sigma\) is the plume width; note that a super-Gaussian distribution can also be considered as an Exponential Power Distribution [63]. Figure 4 shows that while the super-Gaussian form is a good fit for the majority of the plume (and hence for calculations of thrust and associated efficiency), at the highest plume angles that may impinge the extractor, mass flux was recorded at lower levels than a super-Gaussian fit would predict. The super-Gaussian form was suggested by Thuppul et al. [45] to be a result of polydispersity in the plume, i.e. the sum of many distributions of species. With mass flux dropping even further below super-Gaussian levels at non-extractor-electrode-impinging currents, fluxes measured presently are not expected to change the previous conclusion that negligible mass impinges the accelerator electrode once the beam is accelerated [39].

The absolute value of mass flux for beam currents less than \(\sim\)600 nA drops below detectable levels at angles less than \(\theta _{ext}\), so lifetime is not expected to be affected by mass flux to the extractor electrode for suitably-throttled (<600 nA) emission. If impingement of the extractor electrode is occurring, truncation of the underlying mass flux distribution is expected; accordingly, deviation from the aforementioned super-Gaussian form measured for plumes that are not impinging the extractor can give an estimate of the amount of mass impinging the extractor. Impingement includes two mechanisms. The first mechanism is direct striking of the extractor electrode. The second mechanism is the grazing of species with the aperture edge for angles approaching \(\theta _{ext}\left( Q\right)\); such species experience a relatively higher electric field close to the aperture edge resulting in significant increase in the divergence angle of these species. Truncation of the super-Gaussian profiles is increasingly noticeable above 610 nA, so it is expected that species are beginning to impinge the extractor electrode from 610 nA and up. Above 700 nA, the plume edge is much more sharply cut off, indicating more substantial impingement. At 610 nA and 640 nA, if the super-Gaussian form is taken as an upper bound on the mass flux, the total integrated mass fluxes beyond \(\theta _{ext}\left( Q\right)\) (i.e. that which is impinging the extractor) are 9.44 mg yr\(^{-1}\) and 12.3 mg yr\(^{-1}\), respectively. Such mass fluxes to the extractor electrode should be limited where possible, but would be unlikely to result in electrode saturation over the required lifetime of the device. Between 610 nA and 640 nA a 5% increase in beam current has resulted in a \(\sim\)30% increase in extractor-impinging mass flux; while small increases in beam current can be tolerated without detriment to lifetime, the consequences of increasing the current further increase rapidly, such that operation above 700 nA is not recommended for the presented thruster geometry.

The previously proposed [45] super-Gaussian parameterization of the mass flux profiles persists down to the resolution of the TQCM system (in the absence of electrode impingement), so recommendations can now be made about electrode geometry that minimize electrode impingement over a desired thrust range. The total impinging mass flux, per Eq. 1, can be recast in terms of beam current, \(I_b\), and aperture line-of-sight angle, \(\alpha\) (\(=\theta _{elec}\) in Eq. 1), assuming \(\alpha\) does not substantially alter the extracted plume:

$$\begin{aligned} \dot{M}_{impinge}\left( I_b, \alpha \right) =2\pi r^2\int ^{\frac{\pi }{2}}_{\alpha }{A\left( I_b\right) \cdot \exp {\left\{ -\left( \frac{\theta ^2}{2\left( \sigma \left( I_b\right) \right) ^2}\right) ^3\right\} } \sin {\theta } \textrm{d}\theta }, \end{aligned}$$
(5)

where \(A\left( I_b\right)\) and \(\sigma \left( I_b\right)\) are super-Gaussian scale factor and width respectively as a function of beam current, and the super-Gaussian order has been fixed at \({n=3}\). \(A\left( I_b\right)\) and \(\sigma \left( I_b\right)\) from Thuppul et al. [45] are reproduced in Fig. 5, along with linear fits to the data such that:

$$\begin{aligned} A\left( I_b\right)&=A_mI_b+A_c, \end{aligned}$$
(6)
$$\begin{aligned} \sigma \left( I_b\right)&=\sigma _mI_b+\sigma _c. \end{aligned}$$
(7)

For the data of Fig. 5, the coefficients of Eqs. 6 and 7 are summarized as follows: \(A_{m} = 11.6\) pg cm\(^{-2}\) s\(^{-1}\) nA\(^{-1}\), \(A_{c} = 5.41\) ng cm\(^{-2}\)s\(^{-1}\), \(\sigma _{m} = 0.0351 ^{\circ }\) nA\(^{-1}\), \(\sigma _{c} = 1.42^{\circ }\).

Fig. 5
figure 5

Super-Gaussian parameters of mass flux with beam current from Thuppul et al. [45], with linear fits in red

Full size image

Incorporating Eqs. 6 and 7 into Eq. 5, the integration was performed numerically, and \(\dot{M}_{impinge}\left( I_b, \alpha \right)\) is plotted in Fig. 6 as a function of \(I_b\) for a few values of \(\alpha\). It can be immediately seen that regardless of the choice of aperture diameter, the amount of mass impingement increases rapidly as beam current is increased above a certain threshold; while the super-Gaussian form permits very low electrode impingement at low thrust levels, once the beam does intercept the electrode, growth in mass-impingement is steeper than exponential.

Fig. 6
figure 6

Electrode-impingement inferred from super-Gaussian-parameterized mass flux measurements as a function of beam current (\(I_b\)). Results are shown for a range of aperture line-of-sight angles (\(\alpha\)), indicating that once a threshold beam current is reached the impinging volume increases dramatically

Full size image

Over the range of interest plotted in Fig. 6, an analytical form for the impinging mass at a given \(\alpha\) emerges as

$$\begin{aligned} \dot{M}_{impinge}\left( I_b\right) =M_0\cdot \exp {\left\{ -\frac{b}{\left( I_b-I_0\right) ^2}\right\} }, \end{aligned}$$
(8)

where \(M_0\), b, and \(I_0\) are constants for a given \(\alpha\)Footnote 2. Through iteration of \(\alpha\) and the Eq. 5 integration, \(M_0\), b, and \(I_0\) were found to follow:

$$\begin{aligned} M_0\left( \alpha \right)&= a_1\alpha ^2+a_2\alpha +a_3, \end{aligned}$$
(9)
$$\begin{aligned} b\left( \alpha \right)&= b_1\alpha ^2+b_2\alpha +b_3, \end{aligned}$$
(10)
$$\begin{aligned} I_0\left( \alpha \right)&= c_1\alpha +c_2, \end{aligned}$$
(11)

where \(a_1, a_2, a_3, b_1, b_2, b_3, c_1,\) and \(c_2\) are parameters to fit the function to the data, whose values determined for the present study are reported in Table 1. \(\dot{M}_{impinge}\left( I_b, \alpha \right)\) is plotted in Fig. 7 as a function of \(\alpha\) for a few values of \(I_b\); as expected, widening the aperture (i.e. increasing the aperture line-of-sight angle) results in rapid reduction in impinging mass flux, with a threshold dependent on the beam current.

Table 1 Best fit parameters for Eqs. 9, 10, and 11
Full size table
Fig. 7
figure 7

Electrode-impingement inferred from super-Gaussian-parameterized mass flux measurements as a function of aperture line-of-sight angle (\(\alpha\)). Results are shown for a number of beam currents (\(I_b\)), indicating that electrode impingement is dramatically reduced by widening the electrode aperture at thresholds that vary with beam current

Full size image

Combining Eqs. (8) to (11) allows a governing equation to be formed to calculate expected electrode mass impingement as a function of both beam current and aperture line-of-sight angle:

$$\begin{aligned} \dot{M}_{impinge}\left( I_b, \alpha \right) =\left( a_1\alpha ^2+a_2\alpha +a_3\right) \cdot \exp {\left\{ -\frac{\left( b_1\alpha ^2+b_2\alpha +b_3\right) }{\left( I_b-\left( c_1\alpha +c_2\right) \right) ^2}\right\} }. \end{aligned}$$
(12)

Equation 12 can be used to estimate an appropriate electrode aperture diameter for a given beam current range and propellant accumulation tolerance. The presented analysis did not include the aforementioned dependence of \(\alpha\) on \(I_b\), and could be considered for further development of the model. However, \(\alpha \left( I_b\right)\) was shown to grow with beam current (Eq. 3), such that values of \(\alpha\) determined by Eq. 12 would be smaller than required to mitigate electrode impingement, serving as a lower bound.

It is important to note that modest changes to \(\alpha\) are not expected to substantially change the results reported in this section. In particular, electrospray extraction is governed by the field near the emitting tip [64], with the response of the fluid being to a far-field boundary condition [65]. As small changes to the aperture diameter (\(D_{ext}\)) are not expected to appreciably change the far-field condition, the extraction field near the emitter tip should remain similar with changes to \(D_{ext}\), therefore the extracted species distribution is not expected to have a strong dependence on \(D_{ext}\). One can also examine changes to the emitter-extractor separation, d, which also affect \(\alpha\). For example, Smith’s [66] equation for estimating onset voltage (\(V_0\)),

$$\begin{aligned} V_0 = A_1\left[ \frac{2Tr_c \cos {\theta _0}}{\varepsilon _0}\right] ^{\frac{1}{2}}\ln {\left( \frac{4d}{r_c}\right) }, \end{aligned}$$
(13)

shows only a weak dependence on d at scales relevant to the CMNT geometry. For Eq. 13, \(A_1\) is an empirical constant, T is surface tension of the ionic liquid, \(r_c\) is the radius of the capillary tip, \(\theta _0\) is the cone angle, and \(\varepsilon _0\) is the permittivity of free space. With dimensions and operating conditions from the acceleratorless CMNT geometry, a 10% change in emitter-extractor separation yields a change in onset potential of 3%, so modest changes to \(\alpha\) through changes in emitter-extractor separation are not expected to substantially change the model results. Further, since the electric field near the emitter tip is relatively insensitive to changes in \(D_{ext}\) and d, modest misalignments are also not expected to substantially change the extraction conditions (in agreement with findings of Demmons et al. [67]). As such, for the impingement calculation (Eq. 5) one must change the value of \(\alpha\) for each geometry, but the integrand would remain the same. While complete measurement and analysis of the mass flux profile as presented is recommended for design of any new electrospray geometry, the forms and numbers presented herein should provide an accurate starting point to determine appropriate scales for electrode design. Additionally, as the potential field near the emitter tip is relatively insensitive to small changes in electrode geometry, the super-Gaussian form is likely applicable to similar capillary-type EMI-Im electrosprays operating at similar extraction voltages.

Overall, the present data and analysis indicate that for a capillary electrospray thruster with appropriately-designed emitter and accelerator line-of-sight, electrode impingement can be negligible during steady state operation as long as the thruster is not operated at too high a beam current. Specifically for the CMNT-type thruster, the threshold for appropriately-throttled beam current is 600 nA, with currents up to 700 nA being tolerable. Fitting to present and previous data [45], we can achieve mass impingement goals [51]. To confirm this assertion, a life test of the thruster operating below 600 nA is recommended, and expected to yield favorable results.

Conclusion

A TQCM in an electrospray plume provided a five-fold improvement in mass flux resolution (\(\sim\)2 pg cm\(^{-2}\)s\(^{-1}\)) over previously reported QCM measurements (\(\sim\)10 pg cm\(^{-2}\)s\(^{-1}\)) [45]. The electrospray meniscus was measured to grow with increasing beam current, increasing the electrode line-of-sight angle by \(\sim\)2\(^{\circ }\) to 3\(^{\circ }\) over the measured beam current range. An \(n=3\) super-Gaussian form (or exponential power form) provided an appropriate fit to the mass flux as a function of polar angle in the absence of extractor impingement at all beam currents, down to the noise floor of the TQCM in HOAGIE. For the investigated electrospray geometry, the mass flux at the extractor line-of-sight angle dropped below measurable levels at beam currents less than 600 nA; analysis shows that operation below 600 nA yields desirable lifetime for the CMNT geometry. Above 600 nA, a small amount of electrode impingement was detected that increases very rapidly relative to the increasing beam current, such that operation above 700 nA is not recommended for the given geometry. A data-driven model was developed for estimating electrode impingement as a function of beam current and aperture line-of-sight, quantitatively capturing the rapid increase in mass flux at higher beam currents or at low angles. Electrosprays operating in droplet mode can be designed to operate at beam currents that produce appropriate thrust and negligible extractor and accelerator impingement.