Abstract
Air breathing electric propulsion (atmosphere-breathing electric propulsion) (ABEP) has attracted significant interest as an enabling technology for long duration space missions in very low Earth orbit (VLEO) altitudes below about 300 km. The ABEP spacecraft and mission analysis model developed allows parametric characterization of key spacecraft geometry and thruster performance parameters such as spacecraft length-to-diameter, the ratio of solar array span to spacecraft diameter, thrust-to-power, effective exhaust velocity, and inlet efficiency. For the missions analyzed ABEP generally outperforms conventional electric propulsion (EP) below 250 km altitude. Using a 6U spacecraft architecture the model shows that below 220 km ABEP is the only viable propulsion option for desirable mission lifetimes. Parametric evaluations of key spacecraft and ABEP characteristics show that the most significant technological improvements to ABEP spacecraft performance and range of applicability for VLEO missions will come from advancements in inlet efficiency, low drag materials, solar array efficiency, and thrust-to-power.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Recently, many mission designers are considering very low Earth orbit (VLEO) below 450km for individual spacecraft missions and large spacecraft constellations due to several mission benefits including ease of orbital access, reduced debris environment, a reduced radiation environment, improved communication link budgets, increased resolution and performance for Earth observation sensors, and the possibility of using aerodynamic surfaces for orbital maneuvers, attitude control, and momentum wheel desaturation [1]. Orbits below 450 km require drag compensation to avoid orbit decay. At orbital altitudes between 150 - 300 km atmospheric drag is the dominant perturbing force on a spacecraft orbit [2]. Operating in VLEO is difficult due to the large impact atmospheric drag has on the orbit, and onboard propulsion is required to compensate for drag and maintain the orbit. High efficiency electric propulsion (EP) has been used for drag compensation in VLEO, two notable examples being ESA’s GOCE and JAXA’s SLATS missions which both employed high Isp gridded ion thrusters [3,4,5]. For long duration missions at low altitudes, propellant requirements using conventional EP technology become prohibitively large. Air-breathing EP (ABEP) aims to remove these propellant constraints by collecting air from the local atmosphere to use as propellant. Multiple organizations are currently developing ABEP technologies based on a variety of EP devices [6].
Several ABEP thruster and inlet systems have been investigated in the literature, providing a range of feasible performance metrics for these systems [7,8,9,10,11,12]. Performance metrics such as inlet and thruster efficiency can be connected to overall spacecraft performance via system analysis. An initial system level analysis was performed by ESA which investigated the altitude range where ABEP would become favorable over conventional EP and found that above 250km altitude, conventional EP provides adequate performance and ABEP is not needed [13]. In 2010, Jackson estimated the operating altitudes of standard CubeSat bus geometries by finding the power limited and thrust limited orbital altitudes [14]. Singh presented a VLEO air collection feasibility study in 2014 providing performance equations for multiple ABEP architectures including stored propellant concepts[15]. In 2019 SITAEL presented a system optimization for their ABEP concept [16]. This work yielded three feasible spacecraft geometries for different operational altitudes. Tisaev et al. presents more general analysis of ABEP performance demonstrating the impact of thrust to power, Isp, inlet efficiency, and other performance metrics on operational altitudes [17]. The authors also determine a maximum operating altitude by setting a minimum gas density for thruster operation. Additionally, a thruster controller was developed to maintain orbital altitude and avoid divergent altitude envelopes. Many of the previous ABEP studies have been focused on a specific concept and are not generally applicable. While the analysis presented by Tisaev et al. is general to arbitrary spacecraft, it is limited to dawn-dusk Sun-synchronous orbits. The objective of this paper is to extend the work done by Tisaev et al. to arbitrary orbits which may not always be in sunlight and elliptical orbits which extend to lower altitudes at perigee. Additionally, this work relates spacecraft geometry scaling relations to operational performance independent of the overall size of the spacecraft thus making this analysis general to CubeSats as well as conventionally sized spacecraft. Spacecraft heating is ignored for this analysis as previous authors have shown that heating only becomes an issue at altitudes lower than those investigated in this paper [17, 18]. Additionally, Earth oblateness perturbations are ignored in this study for simplicity and drag is assumed to be the only orbital perturbation.
As ABEP technology moves forward in development, mission planners will require first order analytical tools to evaluate ABEP spacecraft performance, and ABEP developers require direction for which technological areas will yield the best results. We have developed a model for ABEP spacecraft performance dependence on spacecraft geometry and thruster parameters by a combination of spacecraft drag models, atmosphere models, a simple EP thruster model, and basic orbital dynamics. A parametric sweep is performed to determine the optimal geometry and thruster type for an ABEP spacecraft. ABEP spacecraft performance is then compared to conventional EP performance to determine where ABEP becomes favorable in comparison to conventional EP. A discussion of the sensitivity of performance metrics is provided to guide future development of ABEP technology.
Approach
To maintain a persistent orbit and avoid semi major axis decay, the propulsion system must provide thrust to counteract the non-conservative force of drag on the spacecraft. Therefore, to examine ABEP performance for drag compensation we compare solar-powered ABEP thrust against spacecraft drag as described in the following subsections. For this analysis, we do not explicitly account for second order effects such as J2 perturbations.
VLEO environment
Drag is the most significant consideration for VLEO orbits due to the significant interactions between the spacecraft and Earth’s upper atmosphere. Atmospheric conditions in VLEO can be found using one of the many Earth atmosphere models. Popular atmospheric models are the 1976 U.S. Standard Atmosphere, Jacchia 1977, NRLMSISE-00, and GOST, all with their own strengths and weaknesses [19,20,21,22,23]. The NRLMSISE-00 model was chosen for this analysis as it provides accurate information on atmospheric composition, which is useful for ABEP analysis and is shown as Fig. 1 [24].
Atmospheric density at VLEO altitudes is largely dependent on solar activity, but also varies significantly with latitude, longitude, and geomagnetic activity. Variations in density are milder at VLEO altitudes than at higher altitudes with density changing by roughly a factor of 2 between solar minimum and solar maximum and varying by up to 25% from the mean density in latitude and longitude [25].
With these considerations, our analysis uses an average value for density across all latitude and longitudes and is constrained to median geomagnetic activity (Ap = 8). Where stated, three solar activity conditions will be investigated: solar minimum (10.7cm flux = 62 SFU), mean solar activity (10.7cm flux = 114SFU), and solar maximum (10.7 cm flux = 200 SFU). 10.7 cm solar radio flux has historically reached up to 250 SFU, but 200 SFU offers a realistic mean for sustained solar activity across multiple solar cycles as shown in Fig. 2.
Historical 10.7 cm radio flux showing the 11 year solar cycle. Marked values for solar minimum, average solar conditions, and solar maximum are marked at 62 SFU, 114 SFU, and 200 SFU. Data taken from [26]
ABEP thrust analysis
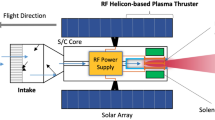
ABEP thruster systems consist of an inlet which collects air from the atmosphere and an EP thruster which ionizes and accelerates the propellant collected by the inlet as shown in Fig. 3. Air is made up of multiple species, so thrust is given as a summation of the individual thrust contribution from each species:
where cs is the exhaust velocity of each species, \(\dot {m}_{s}\) is the exhaust mass flow rate of each species, ηm takes into account neutral particles lost due to diffusion out of the thruster which contribute negligible thrust, and γ is a loss factor which takes into account thrust reduction caused by beam divergence and the presence of doubly charged ions. This mass flow rate can be expressed as the product of particle flow rate, \(\dot {N}_{s}\), and the individual particle mass, M, such that \(\dot {m}_{s}=\dot {N}_{s} M_{s}\). Generally, molecular species are not conserved due to dissociation and recombination in the thruster. \(\dot {N}_{s}\) is dependent on thruster geometry and plasma conditions inside the thruster, and accurately computing \(\dot {N}_{s}\) requires a reacting plasma code which is outside the scope of this work. This analysis will assume frozen flow throughout the thruster such that \(\dot {N}_{collected_{s}} = \dot {N}_{exhaust_{s}}\) The particle flow rate effectively captured by the inlet can be expressed as,
The inlet efficiency ηin is defined as the ratio of incident mass flux that is transmitted through the inlet to the propulsion system [27]:
The incident mass flux not transmitted through the inlet, \(\dot {N}_{reflected}\) is reflected back out of the front of the inlet. Inlet efficiency, ηin, is the key performance parameter for the inlet of an ABEP device and sensitivity of this parameter to ABEP performance mission capabilities will be assessed in the forthcoming analysis. While active inlets have been shown to achieve high ηin and high compression ratio, passive inlets are more widely covered in the literature; thus, this analysis will be limited to passive inlets [28, 29]. Passive inlets generally rely on two capture methods: diffuse capture with collimators and an accumulator chamber and specular capture with a conical or parabolic inlet [14, 30, 31]. Atomic oxygen adsorption on surfaces leads to surface roughening and more diffuse scattering over time [32]. Specular collection methods rely on materials which can resist surface roughening and maintain persistent specular reflection. Such materials are currently under investigation [33], but none currently exist, so this work will be limited to diffuse collimator-accumulator designs [10, 27]. Previous investigations have shown that for passive collimator-accumulator type inlets ηin varies with inlet geometry and is inversely proporational to compression ratio of the inlet [12, 34]. Collimator-accumulator type inlets have been proposed in literature with ηin ranging from 20% to >45% [30, 31]. Higher inlet efficiencies can be achieved at the cost of gas compression but this is generally considered undesirable [12, 34]. For this work ηin=0.35 is assumed to be a reasonable estimate for applicable to a wide range of systems [27, 29, 35].
Ain in Eq. 2 can be replaced with (Ain−AexΘ) to capture the effect of particles passing completely through the inlet and thruster system and exiting out the back of the spacecraft without colliding with the spacecraft or another particle. Θ is the line-of-sight open area fraction at the exhaust plane. ABEP designs with no direct line-of-sight from the inlet through the thruster, such as the JAXA design described in [7], have Θ=0. Equation 2 assumes collisionless flow throughout the system. The increased air density inside the inlet and thruster system may cause collisions further reducing the number of particles which pass through the spacecraft without interacting. While the ambient flow is considered free-molecular with little inter-particle collisions, the inlet can compresses the flow to the point where inter-particle collisions become important. A multiplicative factor ζ may be applied to Aexϕn to account for the gain in \(\dot {m}\) due to increased particle collisions, where ζ ranges between 0 and 1 for full collisional and full collisionless flow respectively. Equation 2 then becomes \(\dot {N}_{s} = \eta _{in}n_{a_{s}}u_{\infty }\left (A_{in}-A_{ex}\Theta \zeta \right)\). For common ABEP designs inlet area is much larger than thruster exhaust area, Θ is generally small for HETs and gridded ion thrusters, and ζ is small for high compression inlets, so Ain>>AexΘζ and AexΘζ is a small correction. Under these assumptions, including AexΘζ has little impact on final ABEP performance, so for this study it is assumed that AexΘζ≈0. ABEP concepts utilizing weakly compressing inlets, large exhaust areas, or high Θ should include the expansion Ain→Ain+AexΘζ.
The exhaust velocity cs for singly ionized species under electrostatic acceleration is given by:
Equation 4 is valid for thrusters relying on electrostatic acceleration of ionized propellant such as Hall-effect thrusters and gridded ion thrusters. Combining Eqs. 1, 2, and 4 yields the thrust of an ABEP device assuming frozen flow:
Given a maximum mass utilization efficiency, the maximum thrust for an ABEP system can be found with Eq. 5. Maximum thrust for a given altitude is limited by thruster performance parameters, inlet size, and inlet efficiency.
Additional seed gas propellant such as xenon can be mixed with the collected air to produce additional thrust or reduce the thrust to power (T/P) of the device. These air augmented thrusters can be described by an additional term in the thrust equation:
In this case thrust is not limited by operating altitude and thrust can be increased by using onboard propellant. Equation 6 provides a first order description of the thrust produced by an ABEP device. System analysis with mixing air and onboard propellant is outside the scope of this study, so this paper will focus on the fully air-breathing case where \(\dot {m}_{fuel} = 0\) described by Eq. 5.
Drag
VLEO orbits are hallmarked by drag being the dominant perturbing force on a spacecraft, therefore, understanding and properly modeling drag forces is one of the most influential elements of spacecraft performance modeling in VLEO. Drag is dependent on geometry, attitude, and surface properties. In order to create a standard drag model, a reference spacecraft bus geometry is defined as shown in Fig. 4.
The geometry is defined by the bus diameter d, the ratio of length to diameter L/d, and the ratio of the solar array length to diameter s/d, or effectively how many folding solar array panels the geometry employs. The thickness of the solar arrays is defined by the ratio tSA/s which can be extrapolated from COTS solar array panels. This study will use tSA/s=0.0083 which was determined from CubeSat solar arrays [36]. Defining the geometry in terms of the diameter allows the spacecraft size to be scaled entirely by it’s diameter, and it will be shown in later sections that overall performance is independent of size and only dependent on L/d and s/d.
Flow regimes and particle-wall interactions
Knudsen number (Kn) is defined as the ratio of the mean free path to a length scale. Kn is used to determine the type of flow model that is applicable to the problem [37]. Low Kn flows (Kn <0.01) are considered continuum flows and the gas-dynamics are dominated by particle-particle collisions. High Kn flows (Kn >10) are considered free-molecular where particle-wall collisions are more frequent than particle-particle collisions, and the gas-dynamics are dominated by particle-wall interactions. Statistical mechanics and direct simulation Monte Carlo (DSMC) methods are frequently applied to free-molecular flows [38]. Intermediate Kn values (0.1 < Kn <10) are considered transitional flows where particle-particle and particle-wall collisions are equally important.
Kn remains in the free-molecular flow regime for spacecraft as large as 1 m in diameter for altitudes above 150 km [33]. In free-molecular flows, after impacting a wall, the incident particle is reflected specularly, diffusely, or a combination of the two [39]. Specular reflection is akin to light reflecting off a mirror where the angle of incidence and the angle of reflectance are the same. Specular reflection usually occurs at clean, smooth surfaces. Rough surfaces lead to diffuse reflections where the angle of reflectance is determined by a Lambert cosine distribution. The degree to which a particle is specularly or diffusely reflected is determined by the accommodation coefficient σ, with σ=1 corresponding to completely diffuse reflection and σ=0 corresponding to completely specular reflection [39]. Thus, σ strongly influences the drag coefficient of the spacecraft.
Drag model
The atmosphere at VLEO altitudes is rarified with large mean free path lengths leading to high Kn and free-molecular flow conditions. There are a number of analytical free-molecular flow drag models in literature [39,40,41]. The Storch drag model was chosen for this analysis, and the full equation for the flat plate drag coefficient is given as [39]:
It has been shown in the literature that spacecraft accommodation coefficients are very near 1 at VLEO altitudes due to adsorption of atomic oxygen to the surface increasing its roughness [32, 42, 43]. Applying the σn=σt=1 assumption to Eq. 7:
The reference geometry is comprised of multiple flat plate surfaces oriented either normal or parallel to the flow direction. We can then constrain Eq. 8 to only the normal incidence, α=90 deg:
and parallel, α=0 deg, incidence angles:
Where the speed ratio S is defined as \(S\equiv \frac {u}{V_{a}}\) [39]. Figure 5 shows variation in CD with altitude for the normal and parallel incidence angles. \(C_{D_{\perp }}\) does not change much over the altitude range, but \(C_{D_{\parallel }}\) varies significantly with altitude increasing by more than 25% from 150 to 250 km altitude.
Drag on the front facing inlet is due to a combination of reflected particles described by the \(C_{D_{\perp }}\) given by Eq. 9 which produce a drag force of \(D_{reflected} = \frac {1}{2}\rho u^{2} A_{in} C_{D_{\perp }}\) and ram drag due to particles captured by the inlet. Captured particles are described as inelastic collisions which impart a drag force of Dinelastic=ρu2Ain. The ratio of reflected to absorbed particles is given by the inlet efficiency ηin defined by Eq. 3. Thus the total drag force on the inlet can be written as Din=(1−ηin)Dreflected+ηinDinelastic or [16, 44]:
For a flat plate at normal incidence CD≈2.13 over the VLEO altitude range making the two terms in Eq. 11 almost the same, and thus ηin has little effect on drag.
Drag on the full spacecraft can be broken into two components: inlet drag and skin friction drag given by D=Din+DSF. Inlet drag is necessary for ABEP operation as there must be an inlet to collect air from the atmosphere. Skin friction drag is unnecessary drag which can be reduced through the use of low drag materials with low accommodation coefficients. Summing the drag force on each surface yields the total drag force on the spacecraft:

Through the way the reference geometry was defined, the total spacecraft drag is proportional to Ain=d2.
Drag can be expressed as \(D = \frac {1}{2} \rho u_{\infty }^{2} A_{in} C_{D_{eff}}\) by defining an effective coefficient of drag:
6A breakdown of the drag contribution from each surface for two 10cm diameter spacecraft with differing L/d is shown in Fig. 6. Doubling the L/d of the spacecraft from 3 to 6 causes the skin friction drag to overtake frontal area drag as the dominant drag force on the spacecraft. Table 1 outlines the percent contribution from each drag source over the VLEO altitude range. In this table, drag is normalized to a point making drag independent of bus diameter and only dependent on L/d and s/d.
Orbital speed u is mostly constant with altitude for circular orbits in the VLEO altitude range. Atmospheric density ρ is roughly exponentially dependent on altitude, so for a given geometry, drag is dominated by ρ∝ exp(h). ρ is determined using the NRLMSISE-00 atmosphere model for this study.
Power model
EP and ABEP spacecraft require power to drive the propulsion system. Power collected by a solar array is given by PBOL=ηcellηassyηtI0ASA cosθ where θ is the angle between solar array normal and the solar vector [45]. The reference geometry described in Drag section has two deployed solar arrays and body mounted solar panels over the entire length of the spacecraft bus which are angled 45∘ relative to the deployed solar arrays. The maximum available power to this reference spacecraft is given by:
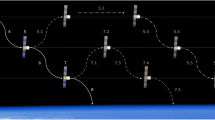
Similarly to drag in Drag model section, Pmax∝d2. Typically, spacecraft will employ a combination of gimballed solar arrays and attitude control to point the solar arrays directly at the sun and collect maximum power. This is not an option in VLEO since the spacecraft must remain oriented with the minimum surface area in the direction of the velocity vector to keep drag at a minimum. At most, a compromise can be struck by rotating the spacecraft about its velocity vector as shown in Fig. 7. The optimum spacecraft attitude for maximum power collection was derived by Singh [15].
Diagram showing the optimal spacecraft attitude which maximizes collected power while keeping the spacecraft oriented for minimum drag. Spacecraft velocity vector is shown in red, solar array normal is shown in blue, orbit normal is shown in purple, and the sun vector is shown in yellow. β is the angle between the sun vector and the orbital plane
The β angle is frequently used in spacecraft power analysis to determine the duration of eclipse periods and is defined as the angle between the orbital plane and the solar vector. Assuming the solar arrays can be rotated arbitrarily about the spacecraft velocity vector to collect the maximum amount of power, the collected solar array power is proportional to the magnitude of the cross product of the velocity unit vector and the solar unit vector: P∝ sinψ where ψ is the angle between the solar vector and the velocity vector. At points 1 and 2 the spacecraft can be rotated such that the solar arrays are directly facing the sun and maximum power is collected. At point 3 the solar arrays make an angle \(\frac {\pi }{2} - \beta\) to the sun. Assuming ψ varies sinusoidally between beta and pi/2 over the course of the orbit we can determine ψ:
Instantaneous spacecraft power available when the spacecraft is not in eclipse is then computed as:
Beta angle analysis can then be applied to determine the eclipse fraction fE of the orbit [46].
Figure 8 shows the normalized power collected over two complete orbits including eclipse periods where no power is collected. Integrating over mean anomaly ν yields the mean power over the orbit as a function of the beta angle shown in Fig. 9.
Power collected over two complete β=30∘, 200 km altitude orbits showing eclipse periods in grey and power reduction due to solar array cosine losses. Power is normalized to the maximum power collected. These results were verified using the Systems Toolkit software [47]
Normalized mean power collected vs β. High β orbits are in constant sunlight can do not have any eclipse periods. Low β orbits experience significantly reduced average power due to long eclipse periods and high cosine losses. This figure is computed for 200 km altitude, but the results do not vary significantly over the VLEO altitude range
Average power can be reduced by as much as 70% from a sun-synchronous orbit leading to significant decreases in spacecraft performance. The results shown in Figs. 8 and 9 are computed for a 200 km altitude circular orbit, but the results do not change significantly over the VLEO altitude range. This study will be limited to circular orbits and slightly elliptical orbits where the power analysis does not vary significantly from the circular case.
VLEO orbit types
ABEP spacecraft may operate in circular or elliptical orbits. Depending on mission needs, elliptical orbits can provide higher orbit apogee to reduce orbit average drag or allow a lower perigee for improved Earth proximity during part of the orbit. More highly elliptical orbits can be considered to further reduce the minimum operating altitude beyond what is possible with orbits entirely in the range of VLEO. These orbits can have apogee at a higher altitude where drag is reduced and dip to low altitudes near the Earth at perigee. These “Super Low Perigee Orbits” (SuLPO) can provide benefits to certain space missions by bringing the spacecraft very close to Earth for a portion of the orbit.
Results
Power limited altitude
A power-limited minimum operating altitude of any EP spacecraft can be determined through a power balance between the power required to compensate for drag, which is dependent on altitude, and the average power collected by the solar arrays over each orbit. Power required to compensate for drag is determined from the T/P of the propulsion system:
For a given geometry, average power available can be computed from the power model described in Power model section, and drag can be determined as a function of altitude using Eq. 12. T/P is typically determined for each individual ABEP technology. Using the drag model, the power model, and an atmosphere model to relate atmospheric temperature and density to altitude, then the power limited minimum altitude can be determined by numerically solving Eq. 24 for altitude.
As shown in Drag model and Power model sections both power available and drag are proportional to d2. Scaling spacecraft diameter increases drag, but also scales the solar array size providing more power collected to compensate for drag. This scaling effect cancels in Eq. 24 decoupling spacecraft performance from spacecraft diameter. Thus performance is only a function of \(\frac {L}{d}\) and \(\frac {s}{d}\). For example, a 3U CubeSat with 20cm long solar arrays (10 cm ×10 cm ×30 cm, L/d = 3, \(\frac {s}{d} = 2\)) can operate at the same altitudes as a larger scaled 1m ×1 m ×3 m, L/d = 3, \(\frac {s}{d} = 2\) spacecraft provided T/P is the same for both propulsion systems. In practice, for a given type of thruster, larger thruster systems typically offer greater efficiency than smaller EP thrusters. Figure 10 show the power limited minimum operating altitude for an EP or ABEP VLEO spacecraft with varying geometry and T/P.
Conventional HETs and gridded ion thrusters typically have high T/P in the 30 - 65 mN/kW range [48, 49] while ABEP propulsion has lower T/P in the 10 – 30 mN/kW range [8, 10] due to decreased performance from atmospheric propellants. Higher L/d spacecraft with larger solar arrays are able to collect more power and operate at lower altitudes. T/P has the greatest impact on the power limited minimum altitude, and improving T/P for the propulsion system leads to large decreases in operating altitude. Figure 11 shows how improving T/P reduces the power limited minimum altitude for a reference 6U geometry shown in Fig. 6 at different solar activity levels. For this geometry, minimum operating altitude varies by up to 20 km over the solar cycle. Increasing T/P yields diminishing returns at lower altitudes approaching 150 km where atmospheric density increases rapidly as shown in Fig. 1. Another concern is larger spacecraft operating at lower altitudes can approach the threshold for the transitional flow regime leading to further increases in drag not accounted for by this model.
T/P vs power limited minimum operating altitude for the 6U reference geometry shown in Fig. 6 (L/d=6,s=2). Current air-breathing gridded ion thrusters achieve T/P = 10 mN/kW, inductive plasma thrusters can achieve T/P = 20 mN/kW [8, 50], and current air-breathing HET thrusters can achieve T/P = 30 mN/kW [10]. Minimum altitude varies by up to 20 km over the solar cycle for this geometry
Thrust to drag ratio
In order for a spacecraft to maintain a stable orbit and avoid semi-major axis decay, adequate thrust must be produced to compensate for drag T≥D, or T/D≥1. Equation 5 gives the thrust produced by an ABEP system, and Eq. 17 gives the drag on the spacecraft. Combining Eqs. 5 and 17 and substituting \(\sqrt {M_{s}}n_{a_{s}} = \frac {\rho _{s}}{\sqrt {M_{s}}}\) where ρs is the partial density given as \(\rho _{s} = \mathscr {C}_{s} \rho\):
\(\mathscr {C}_{s}\) is the mass fraction of each species in the atmosphere. The ρ dependence has dropped out of Eq. 25 removing any strong dependence on altitude. u∞ varies slightly over the VLEO altitude range, and \(C_{D_{eff}}\) is also weakly dependent on altitude through the speed ratio S and the ambient mean thermal velocity Va. Ms varies slightly over the altitude range due to composition changes in the atmosphere. Therefore T/D is mostly constant with altitude shown in Fig. 12. Additionally, if AexΘn<<Ain, which is generally desirable to minimize propellant loss, then dependence on Ain also drops out of Eq. 25.
As L/d and s/d increases, drag increases as well, but the maximum thrust produced remains constant due to the constant inlet size. High L/d and s/d ABEP spacecraft have T/D<1 and therefore cannot maintain a stable orbit. High power spacecraft are desirable to reduce the power limited minimum operating altitude, but high power spacecraft also suffer from low T/D which could make the geometry unviable if T/D<1.
Parameter sweep
The power limited minimum altitude model and the T/D model can be applied in a parameter sweep over a range of spacecraft geometries, thruster T/P, and orbit β angles to map these inputs to minimum operating altitude and T/D. Geometries with L/d between 3 and 10 and between 1 and 4 solar array panels are investigated. L/d>10 and s/d>4 are considered unrealistic and not structurally sound. Current gridded ion thrusters running on atmospheric propellants achieve T/P≈ 10 mN/kW while current Hall thrusters running on atmospheric propellants can achieve T/P≈ 30 mN/kW [8, 10]. A range of T/P between 10 - 30 mN/kW is chosen to encompass the full range of current ABEP technology. β angles ranging from 0∘ to 90∘ encompasses the entire range of possible orbit cases. For each combination of inputs, the minimum T/D is checked to ensure T/D≥1. T/D is roughly constant with altitude, so only checking the minimum is considered sufficient for this analysis. Minimum operating altitude is then determined by the power limited minimum altitude analysis described in Power limited altitude section. T/D is computed for the power limited minimum altitude.
Figures 13 and 14 show the results of the parameter sweep with Vb=1500 V and Figs. 15 and 16 show the results of the parameter sweep with Vb=500 V. Current ABEP gridded ion thrusters have a T/P of 10 mN/kW and can support an ABEP spacecraft at a minimum of 175 km. ABEP HETs have a T/P of 30 mN/kW, but cannot provide as high T/D due to lower effective exhaust velocity per Eq. 25 and can support a spacecraft to as low as 155 km. Geometries with T/D=1 are viable, but spacecraft designers may wish to use designs with slightly higher T/D to improve maneuverability and spacecraft survivability in unexpected environmental conditions. Aerodynamic maneuvering and orbit changing requires T/D>1 to accommodate increased drag during these maneuvers.
Minimum operating altitude for a range of spacecraft geometries, T/P, and β for an ABEP with Vb=500 V, ηm=0.85,ηin=0.35, and γ=1. Cases with T/D<1 are blacked out. High β orbits offer lower altitude operation since they offer more power to the spacecraft. Note for Vb=500 V lower T/D is achievable than the high Vb case shown in Fig. 13 and only low drag geometries are feasible
Actuated solar arrays can be retracted during eclipse periods when they do not collect power to reduce drag. The mean drag over a complete orbit is computed as a weighted average of the total spacecraft drag with the solar arrays deployed and the total drag with the solar arrays retracted:
where the weighting factor fE is the eclipse period computed from a beta angle analysis. Retracting solar arrays reduces minimum operating altitude by up to 10km for geometries with large solar arrays. The added mass and complexity of actuated solar arrays may outweigh the relatively minor benefits. Additionally, atmospheric density is usually reduced on the eclipse side of the Earth further reducing the benefit of retracting the solar arrays during eclipse periods. Equation 26 is only valid for circular orbits. Elliptical orbits may benefit more from retracting the solar arrays for certain portions of the orbit, but that analysis is outside the scope of this study.
Comparison between conventional EP and ABEP
Conventional EP spacecraft operating in VLEO can be analyzed using the drag model from Drag model section, and propellant requirements can be determined from mission lifetime and drag compensation requirements. The parametric analysis in Parameter sweep section shows that a spacecraft with L/d = 6 and s/D=2 is found to perform well. A 6U ABEP CubeSat shown in Fig. 17 can be directly compared to a conventional EP 6U spacecraft using the same bus. This analysis is similar to the analysis of a high ΔV CubeSat [51].
6U cubeSat with conventional EP
A total volume of 6U is provided by the spacecraft bus, and the subsystem layout is shown in Fig. 18. The propulsion unit is assumed to occupy 1.6U of volume based on commercial CubeSat EP thrusters [52]. COMMS, ADCS, and EPS are estimated to occupy 1.5U of volume in the spacecraft [51]. EPS mass is estimated to be 0.14 kg [53]. This leaves 2.9U for propellant and payload. The propellant tank is assumed to be at a temperature of 322 K and pressure of 161 bar [51]. As the propellant requirements grow, the propellant tank grows as a sphere until it is 9 cm in diameter, then it becomes stretched to become a cylinder [51].
Figure 19 shows the effect on payload volume vs spacecraft altitude and mission lifetime. At lower altitudes, the remaining payload volume decreases until there is no payload volume remaining and the spacecraft reaches its minimum altitude. The lifetimes shown in Fig. 19 are in agreement with previous studies [9, 13] Similarly to high ΔV spacecraft, thruster Isp has a major impact on propellant requirements. Spacecraft wet mass increases at lower altitudes and longer mission lifetimes due to the increased propellant mass required for low altitude and long mission lifetimes. The 6U reference spacecraft has an estimated 5.3 kg dry mass not including propellant tank mass. Figure 20 shows how wet mass increases with increasing mission lifetime and decreasing operating altitude. The reference spacecraft can collect 96 W at peak solar power. For orbits that are not sun-synchronous with low β angles, the mean power collected is reduced by eclipse periods and non-optimal solar array pointing as shown in Power model section. Lower altitude orbits require more thruster power to compensate for drag leaving less power available to the payload and other systems. Figure 21 shows the remaining power available to the spacecraft for a variety of orbit types. Lower altitude orbits leave very little power remaining for subsystems, and the power limited minimum altitude is considered where all of the available power is sent to the propulsion system to compensate for drag and the remaining power is zero. In practice, the minimum operating altitude will be above the power limited minimum altitude due to power draws from other subsystems.
Power available to the payload and other subsystems for a 6U CubeSat operating in VLEO with a T/P=30 mN/kW EP propulsion system [52]
6U ABEP CubeSat
The same 6U bus is now investigated for an ABEP propulsion system. Again, the bus provides 6U of total volume with 1.5U allotted to electronics and 1.6U allotted to the propulsion unit. The air handling system (AHS) includes the inlet and a tube that runs the length of the spacecraft to deliver air from the inlet in the front of the spacecraft to the thruster in the back as shown in Fig. 22. ABEP spacecraft designers will need to take the AHS into consideration when planning spacecraft layout. AHS volume was estimated to be 0.54U. The remaining payload volume is then determined to be a constant 2.36U. The mass of the spacecraft is estimated using data from [51, 52] to be 8.05 kg including a standard mass margin [54]. ABEP spacecraft are lighter and less complicated than conventional EP spacecraft operating at similar altitudes since ABEP does not require heavy propellant, tankage or plumbing. Tables 2 and 3 show the complete mass and volume allocation for both the ABEP and conventional EP 6U reference spacecraft.
Block diagram of the 6U ABEP CubeSat Layout. This layout is similar to ABEP CubeSat layouts described by Jackson [14]
Figure 23 shows the remaining power available to the payload and other onboard systems. The minimum altitude is where the power available goes to zero and the spacecraft sends all available power to the propulsion system. High β orbits are favorable to provide larger amounts of power to the spacecraft and allow for lower altitude operation.
Super low perigee orbit analysis
The power limited minimum altitude of a SuLPO spacecraft can be found using an energy balance between the average power collected on orbit and the energy lost to drag over the orbit:
Where P ̄ is given by Eq. 23 and drag is given by Eq. 17. Figure 24 shows the power limited minimum altitude for a range of geometries and apogee altitudes. SuLPO can have extreme instantaneous power requirements as shown in Fig. 25. These instantaneous power requirements can limit the minimum altitude above the energy limited minimum altitude. Advanced, high-power propulsion technologies such as capacitor driven MPD thrusters may be desirable for SuLPO missions.
Discussion
The model results show that ABEP spacecraft can provide a unique and desirable mission capability for VLEO below 250 km. In contrast, conventional EP is favorable for shorter mission lifetimes at higher altitudes. The primary restrictions for EP for lower altitudes and longer mission lifetimes is due to propellant tank volume significantly reducing usable payload volume, as well as increasing overall mass of the spacecraft. Therefore, high Isp EP is still the favorable choice for moderate mission lengths at higher altitudes. At lower altitudes and longer mission lifetimes, ABEP provides more payload volume than conventional EP, albeit less payload power. At lower altitudes ABEP is limited to high β orbits due to a combination of long eclipse times and SA cosine losses. Sun-synchronous orbits offer the highest ABEP performance, but as low as β=30∘ orbits are still viable for low-power payloads. β=0 offers the worst ABEP performance and mission designers should avoid these orbits if possible.
Spacecraft with high L/d and large solar arrays are favorable for ABEP spacecraft allowing them to collect large amounts of power to feed the propulsion system. There is a limit to the maximum wetted area of the spacecraft as the thrust is fixed for a given propulsion system and inlet area, and spacecraft designers must check to ensure that their spacecraft geometry can achieve T/D≥1. Higher T/D may be desirable to ensure spacecraft survivability at higher-than-expected atmospheric density or to allow for improved maneuverability. A linear 6U form factor with a 2 panel SA was determined to perform well for an ion thruster based ABEP system offering a T/D=1.35 and a minimum altitude of 179 km in a SSO. HET based ABEP systems benefit from improved T/P relative to ion thrusters but suffer from reduced thrust due to the reduced effective exhaust velocity. A 4U spacecraft with 1 solar array panel offers the best performance for a HET ABEP system with T/D=1.27 and a minimum altitude of 161 km in an SSO. Larger spacecraft with the same geometry scaling provide the same performance provided that the propulsion system offers the same T/P. Larger propulsion systems typically provide higher efficiency which could improve ABEP performance for larger spacecraft.
Compression ratio is a concern for operating ABEP thrusters as a minimum gas density must be maintained inside the thruster for proper operation. This gas density limit constrains the range of possible inlet efficiencies and also sets an upper altitude limit on ABEP operation as described in [17]. Deterioration of ABEP thruster components is a concern due to the highly reactive propellant, and oxygen resistant materials must be chosen to resist thruster erosion. Lotz performed grid erosion measurements a modified RIT-10 thruster and measured minimal erosion with titanium grids over a 500 hour test. Extended lifetime testing and accurate grid modeling is required to ensure thruster operation for longer durations.
ABEP performance can be improved with higher T/P propulsion, improved SA efficiency, low drag materials, and highly efficient inlet designs. Higher T/P enables lower altitude operation for ABEP spacecraft and leaves more power for the payload as less power is required to maintain the orbit. Figure 10 shows the dependence of minimum operating altitude on thruster T/P. HET based ABEP offers higher T/P than gridded ion ABEP, but ABEP HETs are limited to smaller bus sizes due to the reduced effective exhaust velocity. Improved solar array efficiency is desirable for almost every space mission, but ABEP missions benefit by having more power available to the propulsion system and enabling lower altitude operation. Figure 26 shows the minimum operating altitude of an example 6U spacecraft with increasing solar cell efficiency. Low drag materials offer reductions in skin friction drag by retaining a low accommodation coefficient in VLEO altitudes and are currently being investigated by ESA’s SOAR spacecraft [33]. Decreasing accommodation coefficient can facilitate up to a 25 km decrease in operating altitude as shown in Fig. 27. Low drag materials also decrease propellant requirements for low-altitude conventional EP spacecraft. Improvements to inlet efficiency provides higher propellant flow rates to the ABEP propulsion system improving T/D. Increasing ηin from 35% to 45% increases T/D from 1.4 to 1.8 for the 6U reference spacecraft (Vb=1500 V). Higher T/D improves spacecraft maneuverability and improves performance for aerodynamic attitude control and orbital maneuvers.
Conclusion
A model was developed to determine ABEP spacecraft performance based on spacecraft geometry and propulsion performance for VLEO orbits. It was found that spacecraft performance is not directly dependent on overall spacecraft size but rather on important non-dimensional geometric ratios such as spacecraft length-to-diameter (L/d) and solar array span to spacecraft diameter (s/d). Power collected on orbit was shown to be heavily dependent on β angle, leading to up to 70% reductions in average power collected from the SSO case for a VLEO spacecraft. The major drivers of ABEP spacecraft performance were shown to be T/D,ηin,L/d, and s/d. A parametric sweep was applied to find geometries which lead to the lowest operating altitude. Given a geometry optimized for low altitude operation, increasing T/P is the most fruitful way to further reduce the minimum operating altitude. Implementing high-efficiency solar arrays and low drag materials decreases minimum operating altitude as well, but not as significantly as T/D.
ABEP CubeSat performance was compared with a conventional EP CubeSat with the same bus geometry to determine mission scenarios which favor ABEP over conventional EP. It was found that for missions of 3 years or longer, payload volume becomes severely reduced for EP spacecraft below 240 km and ABEP spacecraft become favorable, which is in agreement with previous studies [13]. An eccentric orbit type with perigee below about 160 km, Super Low Perigee Orbits (SuLPO), were presented and characterized as an advanced ABEP mission design. SuLPO missions present a difficult technical challenge due to the high peak power requirements on the order of multiple kWs, but SuLPO may prove to be favorable for certain applications as ABEP and spacecraft power technology matures.
Nomenclature
Acronyms
-
ABEP
Air-Breathing Electric Propulsion
-
ADCS
Attitude Determination and Control System
-
AHS
Air Handling System
-
COMMS
Communication Subsystems
-
COTS
Commercial Off-the-Shelf
-
DSMC
Direct Simulation Monte Carlo
-
EP
Electric Propulsion
-
EPS
Electrical Power System
-
ESA
European Space Agency
-
GOCE
Gravity Field and Steady-State Ocean Circulation Explorer
-
HET
Hall Effect Thruster
-
JAXA
Japan Aerospace Exploration Agency
-
LEO
Low Earth Orbit
-
SLATS
Super Low Altitude Test Satellite (Tsubame)
-
SuLPO
Super Low Perigee Orbit
-
U
A 10cm x 10cm x 10cm “Unit”
-
VLEO
Very Low Earth Orbit
Variables
-
A area, m2
-
a semimajor axis, km
-
Ap geomagnetic index
-
c effective exhaust velocity, m/s
-
CD drag coefficient
-
c ̄ mean thermal velocity, m/s
-
\(\mathscr {C}_{s}\) mass fraction
-
D drag, N
-
d diameter, m
-
ΔV change in velocity, km/s
-
E total specific orbital energy, J/kg
-
fE eclipse fraction
-
h altitude, km
-
I0 incident solar flux, W/m2
-
Isp specific impulse, s
-
kb Boltzmann Constant, J/K
-
Kn Knudesn Number
-
L length, m
-
M mean molecular mass, kg
-
\(\dot {m}\) mass flow rate, kg/s
-
n number density, m −3
-
\(\dot {N}\) particle flow rate, s −1
-
P Power, W
-
q electron charge, coulombs
-
R radius of the Earth, km
-
S speed ratio
-
s solar array length
-
T thrust, N
-
t thickness, m
-
Tth thruster temperature, K
-
u flow velocity, m/s
-
Va most probable thermal velocity, m/s
-
Vb beam voltage, V
-
Vw wall thermal velocity, m/s
-
α angle of attack, rad
-
β orbit beta angle, rad
-
η efficiency
-
μ Earth gravitational parameter, km3s −2
-
ν mean anomaly, rad
-
ϕ transparency
-
ψ angle between the spacecraft velocity vector and the solar vector
-
ρ density, kg/m3
-
σ accommodation coefficient
-
σn normal direction accommodation coefficient
-
σt tangential direction accommodation coefficient
-
θ angle between the solar vector and SA normal, rad
-
Θ line-of-sight open area fraction
-
ζ factor for contribution of collisions to collected particle flow rate
Subscripts
-
a
ambient
-
b
assembly
-
c
spacecraft body
-
d
beginning of life
-
e
solar cell
-
f
effective
-
g
exhaust
-
h
ion
-
i
inlet
-
j
freestream conditions
-
k
mass
-
l
maximum
-
m
neutral
-
n
parallel to the freestream
-
o
perpendicular to the freestream
-
p
reflected
-
q
solar array
-
r
seed gas
-
s
thermal
-
t
transmitted
Availability of data and materials
The datasets generated during and/or analysed during the current study are available from the corresponding author on reasonable request.
References
Crisp, Roberts, Livadiotti, Oiko, Edmondson, Haigh, Huyton, Sinpetru, Smith, Worrall, Becedas, Domínguez, González (2020) The benefits of very low earth orbit for earth observation missions. Prog Aerosp Sci 117. https://doi.org/10.1016/j.paerosci.2020.100619.
Spektor R, Jones KL (2021) A breath of fresh air: Air-scooping electric propulsion in very low earth orbit. Cent Space Policy Strateg.
ESA Earth Observation Portal (2021) GOCE (Gravity Field and Steady-state Ocean Circulation Explorer). https://directory.eoportal.org/web/eoportal/satellite-missions/g/goce. Accessed 09 Nov 2021.
Steiger C, Romanazzo M, Emanuelli P, Floberghagen R, Fehringer M (2014) The deorbiting of esa’s gravity mission goce - spacecraft operations in extreme drag conditions In: 13th International Conference on Space Operations. American Insititute of Aeronautics and Astronautics, Reston. https://csps.aerospace.org/papers/game-changer-breath-fresh-air-air-scooping-electric-propulsion-very-low-earth-orbit.
ESA Earth Observation Portal (2021) SLATS (Super Low Altitude Test Satellite) / Tsubame. https://directory.eoportal.org/web/eoportal/satellite-missions/s/slats. Accessed 09 Nov 2021.
Zheng P, Wu J, Zhang Y, Wu B (2020) A comprehensive review of atmosphere-breathing electric propulsion systems. Int J Aerosp Eng 2020. https://doi.org/10.1155/2020/8811847.
Fujita K (2005) Air intake performance of air breathing ion engines. J Jpn Soc Aeronaut Space Sci 52. https://doi.org/10.2322/jjsass.52.514.
Lotz B (2013) Plasma physical and material physical aspects of the application of atmospheric gases as a propellant for ion-thruster of the rit-type. Dissertation, University of Giessen, Gießen.
Shabshelowitz A (2013) Study of rf plasma technology applied to air-breathing electric propulsion. Dissertation, University of Michigan, Ann Arbor.
Busek Company (2012) Atmospheric Breathing Electric Thruster for Planetary Exploration. https://www.nasa.gov/pdf/636899main_Hohman_Presentation.pdf. Accessed 09 Nov 2021.
Andreussi T, Cifali G, Giannetti V, Piragino A, Ferrato E, Rossodivita A, Andrenucci M (2017) Development and experimental validation of a hall effect thruster ram-ep concept In: 35th International Electric Propulsion Conference, IEPC-2017-377. Electric Rocket Propulsion Society, Cleveland.
Parodi P (2019) Analysis and simulation of an intake for air-breathing electric propulsion systems. Dissertation, University of Pisa, Pisa.
Cara DD, del Amo JG, Santovincenzo A, Dominguez BC, Arcioni M, Caldwell A, Roma I (2007) Ram electric propulsion for low earth orbit operation: an esa study In: 30th International Electric Propulsion Conference, 2007–162. University of Pisa, Pisa.
Jackson SW (2017) Design of an air-breathing electric thruster for cubesat applications. Dissertation, University of Colorado, Boulder.
Singh LA (2014) Very low earth orbit propellant collection feasibility assessment. Dissertation, Georgia Institute of Technology, Atlanta.
Ferrato E, Giannetti V, Piragino A, Andrenucci M, Andreussi T (2019) Development roadmap of sitael’s ram-ep system In: 36th International Electric Propulsion Conference, IEPC-2019-886. Electric Rocket Propulsion Society, Cleveland.
Tisaev M, Ferrato E, Giannetti V, Paissoni C, Baresi N, Fabris AL, Andreussi T (2022) Air-breathing electric propulsion: Flight envelope identification and development of control for long-term orbital stability. Acta Astronaut 191. https://doi.org/10.1016/j.actaastro.2021.11.011.
Young M, Muntz EP, Wang J (2001) Maintaining continuous low orbit flight by using in-situ atmospheric gases for propellant In: Rarefied Gas Dynamics: 22nd International Symposium. American Institute of Physics, Melville.
Vallado DA (2007) Fundamentals of Astrodynamics and Applications. Microcosm Press, Torrance.
(1976) U.S. Standard Atmosphere, 1976.
Jacchia LG (1977) Thermospheric temperature, density, and composition: New models. Technical report, National Aeronautics and Space Administration. https://ntrs.nasa.gov/citations/19770016704.
Picone JM, Hedin AE, Drob DP (2002) Nrlmsise-00 empirical model of the atmosphere:statistical comparisons and scientific issues. J Geophys Res 107. https://doi.org/10.1029/2002JA009430.
Cefola P, Volkov II, Suevalov VV (2008) Description of the Russian Upper Atmosphere Density Model GOST-2004 In: 37th COSPAR Scientific Assembly, vol. 37, 476. European Space Agency, Paris.
MathWorks (2021) Atmosnrlmsise00. https://www.mathworks.com/help/aerotbx/ug/atmosnrlmsise00.html. Accessed 09 Nov 2021.
Walterscheid RL (1989) Solar cycle effects on the upper atmosphere - implications for satellite drag. J Spacecr Rocket 26. https://doi.org/10.2514/3.26089.
National Oceanic and Atmospheric Administration (2021) Penticton 10.7cm Solar Radio Flux. https://www.ngdc.noaa.gov/stp/space-weather/solar-data/solar-features/solar-radio/noontime-flux/penticton/penticton_observed/. Accessed 09 Nov 2021.
Binder T, Boldini P, Romano F, Herdrich G (2016) Transmission probabilities of rarefied flows in the application of atmosphere-breathing electric propulsion In: 30th International Symposium on Rarefied Gas Dynamics: RGD 30.
Li Y, Chen X, Li D, Xiao Y, Dai P, Gong C (2015) Design and analysis of vacuum air-intake device used in air-breathing electric propulsion. Vacuum 120. https://doi.org/10.1016/j.vacuum.2015.06.011.
Romano F, Binder T, Herdrich G, Fasoulas S (2015) Air-intake design investigation for an air-breathing electric propulsion system In: 34th International Electric Propulsion Conference. Electric Rocket Propulsion Society, Cleveland.
Romano F, Espinosa-Orozco J, Pfeiffer M, Herdrich G, Crisp NH, Roberts PCE, Holmes BEA, Edmondson S, Haigh S, Livadiotti S, Macario-Rojas A, Oiko VTA, Sinpetru LA, Smith K, Becedas J, Sulliotti-Linner V, Bisgaard M, Christensen S, Hanessian V, Jensen TK, Nielsen J, Chan Y-A, Fasoulas S, Traub C, García-Almiñana D, Rodríguez-Donaire S, Sureda M, Kataria D, Belkouchi B, Conte A, Seminari S, Villain R (2021) Intake design for an atmosphere-breathing electric propulsion system (abep). Acta Astronaut 187. https://doi.org/10.1016/j.actaastro.2021.06.033.
Zheng P, Wu J, Zhang Y, Zhao Y (2022) Design and optimization of vacuum intake for atmosphere-breathing electric propulsion (abep) system. Vacuum 195. https://doi.org/10.1016/j.vacuum.2021.110652.
Moe MM, Wallace SD, Moe K (1995) Recommended drag coefficients for aeronomic satellites. Geophys Monogr Ser 87. https://agupubs.onlinelibrary.wiley.com/doi/abs/10.1029/GM087p0349.
Crisp NH, Roberts PCE, Livadiotti S, Macario Rojas A, Oiko VTA, Edmondson S, Haigh SJ, Holmes BEA, Sinpetru LA, Smith KL, Becedas J, Domínguez RM, Sulliotti-Linner V, Christensen S, Nielsen J, Bisgaard M, Chan Y-A, Fasoulas S, Herdrich GH, Romano F, Traub C, García-Almiñana D, Rodríguez-Donaire S, Sureda M, Kataria D, Belkouchi B, Conte A, Seminari S, Villain R (2021) In-orbit aerodynamic coefficient measurements using soar (satellite for orbital aerodynamics research). Acta Astronautica 180:85–99. https://doi.org/10.1016/j.actaastro.2020.12.024.
Ferrato E, Giannetti V, Tisaev M, Lucca Fabris A, Califano F, Andreussi T (2022) Rarefied flow simulation of conical intake and plasma thruster for very low earth orbit spaceflight. Front Phys 10:823098. https://doi.org/10.3389/fphy.2022.823098.
Parodi P, Quang DL, Bariselli F (2019) Study of a collector-intake system for vleo air-breathing platforms In: International Conference on Flight Vehicles, Aerothermodynamics and Re-entry Missions and Engineering (FAR). ESA Conference Bureau, Noordwijk.
Clyde Space (2020) Solar Panels Photon. https://www.aac-clyde.space/wp-content/uploads/2021/11/AAC_DataSheet_Photon_original.pdf. Accessed 09 Nov 2021.
Panton RL (2013) Incompressible Flow. Wiley. Wiley Publishing, Hoboken.
Prasanth P, Kakkassery J (2006) Direct simulation monte carlo (dsmc): A numerical method for transition-regime flows - a review. J Indian Inst Sci 86:169.
Storch JA (2002) Aerodynamic disturbances on spacecraft in free-molecular flow. https://apps.dtic.mil/sti/citations/ADA410696.
Sentman LH (1961) Free molecule flow theory and its application to the determination of aerodynamic forces. Technical report, Aerospace Corporation, El Segundo, CA. https://apps.dtic.mil/sti/citations/AD0265409.
Schamberg R (1959) Analytic representation of surface interaction for free molecule flow with application to drag of various bodies. Technical report, RAND Corporation Santa Monica, CA.
Pilinski MD, Argrow BM, Palo SE (2010) Semiempirical model for satellite energy-accommodation coefficients. J Spacecr Rocket 47. https://doi.org/10.2514/1.49330.
Pardini C, Anselmo L, Moe K, Moe MM (2009) Drag and energy accommodation coefficients during sunspot maximum. Adv Space Res 45. https://doi.org/10.1016/j.asr.2009.08.034.
Andreussi T, Ferrato E, Piragino A, Cifali G, Rossodivita A, Andrenucci M (2018) Development and experimental validation of a hall effect thruster ram-ep concept In: 35th International Electric Propulsion Conference 2017. Electric Rocket Propulsion Society, Cleveland.
Wertz JR, Larson WJ (1999) Space Mission Analysis and Design (Space Technology Library). Springer, Netherlands.
Chobotov VA (2002) Orbital Mechanics (AIAA Education Series). American Institute of Aeronautics and Astronautics, Reston.
Analytical Graphics, Inc (2021) Systems Tool Kit (STK). https://www.agi.com/products/stk. Accessed 09 Nov 2021.
Busek Company (2021) Hall Thrusters. https://www.busek.com/hall-thrusters. Accessed 09 Nov 2021.
National Aeronautics and Space Administration (2021) Gridded Ion Thrusters (NEXT-C). https://www1.grc.nasa.gov/space/sep/gridded-ion-thrusters-next-c/. Accessed 09 Nov 2021.
Schönherr T, Komurasaki K, Romano F, Massuti-Ballester B, Herdrich G (2015) Analysis of atmosphere-breathing electric propulsion. IEEE Trans Plasma Sci 43(1):287–294. https://doi.org/10.1109/TPS.2014.2364053.
Samples S, Wirz R (2021) Parametric analysis of high-delta-v cubesat missions with a miniature ion thruster. J Spacecr Rocket 58. https://doi.org/10.2514/1.A34827.
Busek Company (2021) RF Ion Thrusters. https://www.busek.com/rf-ion-thrusters. Accessed 09 Nov 2021.
Ibeos (2021) Standard Products. https://www.ibeos.com/standard-products. Accessed 09 Nov 2021.
(2015) American National Standard Mass Properties Control for Space Systems. American Institute of Aeronautics and Astronautics, Reston.
Code availability
Custom scripts were used for the presented analysis, and are available from the corresponding author on reasonable request. Systems Toolkit by Analytical Graphics was used to confirm custom script results where stated.
Funding
This effort was funded by the Air Force Office of Scientific Research (Award No. FA9550-21-1-0067) and The Aerospace Corporation (University Partnership Program 4600007031).
Author information
Authors and Affiliations
Contributions
All authors contributed to the study conception and design. Material preparation and analysis were performed by Patrick Crandall. The first draft of the manuscript was written by Patrick Crandall and all authors commented on previous versions of the manuscript. All authors read and approved the final manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare that they have no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article's Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article's Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Crandall, P., Wirz, R.E. Air-breathing electric propulsion: mission characterization and design analysis. J Electr Propuls 1, 12 (2022). https://doi.org/10.1007/s44205-022-00009-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s44205-022-00009-8