Time evolution of plasma parameters in the jet of a low-power vacuum arc thruster

Abstract

The plasma parameters temporal evolution of a 30 W-class Vacuum Arc Thruster equipped with a Ni-Cr cathode is examined in the far-field region of the plasma jet. Measurements have been performed 20 cm downstream of the arc region where the plasma is created. The thruster operated at 1 Hz with 25 μs duration current pulses. The maximum current intensity reaches 4000 A about 8 μs after the discharge ignition. The change in the electron density, electron temperature and plasma potential during the short high-current pulse has been obtained by means of time-resolved Langmuir probe measurements. A time-of-flight technique based on a planar probe has been used to determine the mean ion velocity in the plasma jet. In addition, a Faraday cup allowed the determination of the ion current density. The electron density peaks at ∼ 8×10¹⁷ m⁻³ at 12 μs. The electron temperature is above 25 eV at 7 μs and then it stabilizes around 5 eV. Several ion populations are identified. The lowest ion mean velocity amounts to 20 km/s. Interestingly, combining all data allows to assess the ion mean electrical charge and its temporal behavior. The mean charge reaches 12 a few μs after ignition. It decays quickly afterwards and stays unchanged at 2 beyond 10 μs. Analysis of all the results support the idea of two distinct plasma discharge regimes.

Introduction

Vacuum arc thrusters are space electric propulsion systems that operate with a solid propellant. A vacuum arc is triggered in the inter-electrode gap of the thruster, creating a metallic plasma from the vaporization and the ionization of the negative electrode material. Expansion and ejection of this highly ionized plasma at high velocities generates thrust [1]. As the ionization process occurs in a relatively small region and as the plasma is quasi-neutral [2], the vacuum arc thruster (VAT) shows inherent advantages for miniaturization. Unlike Hall Thrusters or Gridded Ion Engines, VATs do not require any external neutralizer. The consumption of a solid propellant through vaporization of the cathode itself suppresses the need of a propellant tank and any gaz feeding system. This gives the ability to reduce the mass and size of the propulsion system. It also increases the reliability of the system, as less components are involved. Moreover, vacuum arc discharges can be pulsed without losses in plasma production efficiency [3]. It is then possible to adapt the duty cycle of a VAT to match the electrical power available onboard a spacecraft.

However, VATs suffer from intrinsic shortcomings such as conductive metal deposition on the insulators, non homogeneous cathode erosion and cathode wear. These limit the perfomances as well as the lifetime of the thruster, resulting in a low total impulse. The unique physical conditions achieved in vacuum arcs are in fact an obstacle to the development of high-performance and reliable VATs. Despite several decades of research efforts, the vacuum arc physics still has some unknown surrounding it. At this stage, more experimental data is needed to better understand the formation of the arc, its dynamics and plasma acceleration mechanisms. In this way, codes and numerical simulations can be made more reliable, allowing new solutions and new architectures to be proposed. The final objective of all on-going studies is the increase in performances and lifetime of VATs in order to meet the requirements of a wide range of space missions.

As the inter-electrode region and the arc itself are difficult to probe, a first reasonable approach is to analyze properties of the plasma jet. The latter is indeed more accessible and less disturbed by insertion of diagnostics. In spite of a relatively easy access, the temporal evolution of fundamental plasma parameters like the electron density and temperature has been poorly investigated in the VAT plasma flow far from the source. In this contribution we present experiments performed with a 30 W-class VAT equipped with a Ni/Cr cathode. The change in time of the electron density, the electron temperature and the plasma potential has been observed at the μs time scale during one typical current pulse. The three quantities have been determined through the analysis of time-varying current-voltage curves of a cylindrical Langmuir probe acquired over tens of current pulses, as explained in the next sections. The ion velocity in the jet has also been assessed with a time-of-flight technique. This quantity is of great interest as it governs to a large extent the thrust level, the specific impulse as well as the thrust efficiency of a propulsive device. In the last part of the study we present ion current density measurements carried out with a Faraday cup far downstream of the arc region. The current density is the main driver for the thrust, so it is a relevant quantity. By combining all experimental outcomes, we finally assess the mean electrical charge of ions in the jet. The charge distribution in vacuum arcs has been the subject of numerous investigations as it is strongly related to the physical mechanisms at the origin of the arc formation and plasma ejection.

Experimental arrangement

Thruster

The VAT under study is the Plasma Jet Pack (PJP) developed by the COMAT French company. This 30 W-class VAT generates a high DC current vacuum arc through the cyclic discharges of a capacitor bank. The cathode-anode voltage is continuously set to 250 V. A triggering system applies several kV for hundreds of ns on the cathode surface, initiating a plasma through an explosive process on a region called the cathodic spot [4]. The high voltage applied during the trigger phase initiates a breakdown by field emission [5] that is followed by a spark and then an arc. During VAT operation a thin metallic layer deposits on the insulator that separates the triggering system and the cathode. Ignition of the discharge is then easier as the breakdown occurs through the conductive layer. Note when the deposited layer becomes too thick it is more difficult to vaporize and the thruster no longer operates properly [1]. After the trigger is switched-off, the arc is forced to propagate to the anode through the existing metal vapor. This second arc discharge allows 3 to 6 kA to flow between the two electrodes depending on the material. Overall, few joules are released into one single PJP discharge. All measurements presented here have been obtained with a 80% Nickel–20% Chromium cathode and a copper anode. Moreover, the pulse frequency was set to 1 Hz to avoid thruster thermal issues.

Figure 1a shows the front view of a laboratory version of the PJP. The 4-legs electrode is here the annular copper anode. The cathode corresponds to the grey center-mounted cylinder. The latter is screwed onto a copper plate directly wired to the capacitor bank. The gap between the anode and the cathode is approximately 1 cm. The trigger electrode is a tiny metal tip placed exactly on the thruster axis. The laboratory version of the PJP can easily be disassembled and modified contrary to the flight version. The power unit is however the same for the two versions. The PJP target performances and characteristics are given in Table 1 for the inclined reader. Figure 1b is a photograph of the arc discharge during a current pulse. As the exposure time of the camera is much longer than the VAT current pulse duration, the picture averages the arc dynamics and motion. The picture nevertheless exemplifies the complexity of the physical phenomena at the origin of thrust generation.

Fig. 1

Plasma Jet Pack thruster: front view (a) and plasma discharge in operation (b)

Table 1 PJP thruster target performances and characteristics

Diagnostics

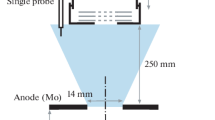
A 19 mm in diameter molybdenum planar probe has been used to record the ion current waveform. The probe was placed 17.5 cm from the anode on the thruster centerline. Plasma parameters have been obtained with a cylindrical Langmuir probe made of tungsten. The probe radius was 0.6 mm and its length was 30 mm. The tip of the probe was placed on the thruster axis 18.5 cm away from the anode. The middle of the tip was then located 20 cm downstream of the anode plane. To determine the ion current density, a 15 mm in diameter molybdenum Faraday cup has been placed 20 cm away from the anode. The current delivered by the three electrostatic probes has been measured by means of a 50 Ω Pearson 2878 current monitor connected to a 1 GHz 12-bit HDO6104A Teledyne LeCroy oscilloscope. The current probe time resolution is ≈ 15 ns.

The discharge current waveform has been recorded on the cathode line with a 50 Ω 2-0.1WA current transformer from Stangenes connected to the Lecroy oscilloscope. The bandwidth is 20 MHz. The instrument can stand up to 10 kA peak current. In order to avoid damaging the high-definition oscilloscope, a voltage divider with an output ratio of 1/10 has been inserted into the circuit, as depicted in Fig. 2. A layout of the experimental arrangement is shown in Fig. 2. Note that all devices are referenced to ground.

Fig. 2

Schematic of the experimental setup for discharge current and plasma jet properties measurements

Experiments have been performed in a 240 l cylindrical stainless steel vacuum chamber. The radius of the chamber is 54 cm and the length is 104 cm. The chamber is equipped with two 2200 l/s-N₂ magnetically levitated turbomolecular pumps (STP-iS2207 series from Edwards) evacuated through a 110 m³/hr dry primary pump (GV110 from Edwards). The background pressure during operation of the thruster is around 10⁻⁵ mbar. The chamber is equipped with several viewports and electrical feedthroughs for the VAT and associated diagnostics. The chamber is grounded to avoid charge buildup and arcing. The VAT, which is placed on a removable stand, has its axis aligned with the tank centerline. The latter also serves as a reference for all electrostatic probes put in the plasma plume.

Traces

Discharge and ion current

A typical VAT discharge current trace is shown in Fig. 3. The t=0 μs time corresponds to the opening of the PJP capacitor bank for energy release into the circuit. The current pulse lasts about 25 μs. The current rises up to 4 kA in less than 10 μs although the input power is only 30 W. Such a large current indicates the thruster generates a very large instantaneous thrust. Assuming the discharge current is entirely converted into singly-charged ion current, the thrust is above 10 N at the peak. Note that as the current transformer is placed upstream of the cathode, see Fig. 2, the fraction of current that goes through the trigger electrode instead of flowing through the anode remains unknown.

Fig. 3

Typical PJP discharge current waveform during one pulse

Figure 4 shows typical ion current traces observed in the plasma jet with the planar probe. The probe was polarized at -75 V to solely capture ions. As can be seen in Fig. 4, current traces are not strictly identical for different pulses although the general shape stays unchanged. This illustrates the fact that vacuum arcs are complex physical phenomena, yet with a certain level of reproducibility and stability. The arc starts to form where the asperities of the cathode give locally a larger electric field, initiating a cathode spot through an explosive phenomenon [4]. As cathode spots have a limited lifetime [6], the arc moves or jumps to other locations on the cathode surface where the electric field is high, initiating other cathode spots. Thus, for a similar discharge current distribution through the cathode, the resulting plasma discharge and plasma jet are different from one pulse to another. However, in the case of the PJP thruster, it is quite common to observe two well-distinct peaks on the ion current profile in the plasma jet for a Ni/Cr cathode, as exemplified in Fig. 4.

Fig. 4

Ion current waveform obtained with a planar probe downstream of the anode (17.5 cm) for 2 current pulses

Langmuir probe

Acquisition of a Langmuir probe I-V characteristic curve is usually performed by smoothly sweeping the probe bias voltage while recording the current [7,8,9,10,11]. The analysis of the measured current against applied voltage curve gives access to the local electron properties and to the local plasma potential [7]. In order to obtain the temporal evolution of a Langmuir probe I-V curve, the voltage frequency sweep has to be much larger than the typical frequency of the observed phenomenon or process. According to waveforms displayed in Figs. 3 and 4, the frequency must be above 1 MHz in this study, which makes measurements extremely complicated for a single shot from a technical viewpoint [12, 13]. Moreover, the evolution of a vacuum arc is fast and stochastic [14], which makes data treatment and analysis challenging. An alternative method is then proposed here to properly recover the change in time of the probe I-V curve in the course of the VAT discharge [15]. This method permits to recover the typical evolution in time of the plasma created during a PJP discharge based on an indirect, or average, approach instead of a direct approach.

The Langmuir probe voltage has been gradually increased from -30 V to +50 V. In order to increase the amount of data and the accuracy, the voltage step was set to 0.5 V between -5 V and 10 V and between 20 V and 30 V. The stepsize was set to 1 V elsewhere. For each voltage step, 20 current traces were recorded and then averaged as the waveform noticeably vary from one pulse to another. The capacitor bank trigger signal is used as a time reference for all recordings. Figure 5 shows the evolution of the mean current trace for various bias voltages. A negative current corresponds here to ions, while a positive current indicates that electrons are captured. As expected, ions are collected when the probe voltage is negative with respect to the ground (reference) while electrons are collected for positive voltages. Besides, the electron current is larger than the ion current in agreement with the Langmuir probe theory. Note that at t=0, i.e. at thruster ignition, a very-high frequency electromagnetic perturbation is always captured by the probes, see Fig. 5.

Fig. 5

Current traces obtained with the Langmuir probe at different voltages (20 cm, on-axis)

Once all waveforms have been acquired over the selected voltage range, a home-made Python program converts the time–current–voltage matrix into a current–voltage–time matrix. In other words, the evolution in time of the probe current for a given voltage is replaced by the change in current as a function of the applied voltage for a given time, or in short the I-V curve for a given time [15]. Figure 6 shows the reconstructed I-V curve at 16.5 μs and 28 μs. As expected the Langmuir probe characteristic depends on the point in time when measurements are performed in the course of the current pulse.

Fig. 6

Reconstructed I-V curves at 16.5 μs and 28 μs

The Langmuir probe analysis is based on the recovery of physical quantities through analytical properties of the Intensity vs Voltage (I-V) curve. Models have been developed to fit experimental data, in order to link properties of the I-V curve to physical properties. The most widely used theory for LP analysis is the Orbital Motion Limited theory (OML). Originally developped by Langmuir and Mott-Smith in 1926 [16], this model assumes an infinite radius of the sheath surrounding the probe. It comes that the ions are attracted from a large distance. A large sheath often implies a low plasma density, and the OML theory should be inaccurate for collisional plasmas. However, Chen showed experimentally in [17] its “surprising” validity for high density plasmas. This theory is popular thanks to its computational simplicity leading to consistent results. Data analysis is indeed based on successive linear fits on the I-V curve, as the $I_{e}^{2}$ vs V slope is proportional to $n_{e}^{2}$.

We however wanted in this study to implement models that takes into account more parameters, in particular a better sheath theory. For achieving this goal, Poisson’s equation should be solved for the potential V(r) that goes from the probe surface to infinity. Chronologically, a theory was first developed in 1957 by Allen, Boyd and Reynolds (ABR) for spherical probes [18] (later extended to cylindrical probes by Chen [19]). ABR theory, although solving the Poisson’s equation, assumes that T_i=0, which would mean that the ions are attracted radially to the probe without any initial velocity.

In reality, though, ions present a finite T_i and are only collected by the probe when their angular momentum is small enough, due to orbital motion around the probe. In order to solve this problem, Bernstein and Rabinowitz developped in 1959 a theory [20] that takes into account a finite ion temperature, assuming mono-energetic ions. Laframboise later extended their work by making the model parametrisation for Maxwellian distributions [21]. This so-called BRL (Bernstein-Rabinowitz-Laframboise) model takes then into account the ion angular momentum, as well as the existence of an absorption radius around the probe. Depending on the probe potential and on the ion angular momentum, some ions are trapped and collected by the probe when they cross this virtual boundary. Hence, the BRL is the most complete theory presented here.

Concerning the electron temperature, the ABR and BRL models give very similar values as they both assume a Maxwellian energy distribution function for the electrons. The electronic part of the I-V curve is then an exponential function between the floating potential and the plasma potential V_p. The electron temperature is determined from the slope of the natural logarithm of the electron current in the transition region: $T_{e} = \left (\frac {dln(I_{e})}{dV} \right)^{-1}$.

The plasma potential V_p can be inferred from the ABR and BRL models. However, the two models provide a value for the ion branch and another one for the electron branch. The two values of V_p do not match under our conditions due to the fact that the electron density is relatively large [7, 22]. For that reason, V_p is classically defined here as the voltage for which the first derivative of the I-V curve is the highest. V_p indicates the inflection point of the curve beyond which the electron current saturates [8,9,10].

Examples of calculation outcomes are presented in Table 2 based on the I-V curves obtained at 16.5 μs and 28 μs, see Fig. 6. The BRL theory always gives an electron density larger than the ABR theory, as observed in the past with low-pressure radio-frequency discharges [22]. The OML model is most of the time in good agreement with the BRL model in this work. The electron temperatures are almost identical as the same approach is used in the two models. The slight difference could be due to the substraction of the ion current.

Table 2 Plasma parameters comparison at two different instants

Time evolution of electron parameters

Electron density

Figure 7 shows the temporal evolution of the electron density during a VAT current pulse computed with the three models, namely OML, ABR and BRL. Before 5 μs the measured Langmuir probe current is very weak and extremely noisy especially for the ion branch of the I-V curve. We therefore decided not to account for the data before 5 μs to avoid misinterpretation. After 30 μs, waveforms were not recorded in this experimental campaign. This was a mistake as the plasma discharge lifetime is longer than the current pulse as illustrated in Fig. 5.

Fig. 7

Time evolution of the electron density at x=20 cm computed with the OML, ABR and BRL models. The solid line shows the discharge current trace for comparison

As can be seen in Fig. 7, the electron density time series are shifted with respect to the discharge current trace. The first electrons are detected approximately 7 μs after ignition of the cathodic arc. Assuming the electron flow with a constant velocity in the plasma jet, the velocity of the first electron group is 28.6 km/s. An interesting fact is the appearance of a density peak at 7 μs of which the width corresponds approximately to the activation time of the high-voltage trigger, see “Thruster” section. After this time lapse the trigger mechanism is switched off and the arc migrates towards the anode that is polarized at 250 V. This corresponds to the small decrease in density around 8 μs. The density subsequently increases to its largest value reached at about 13 μs before slowly decreasing. The evolution in time of the electron density follows the discharge current trace with a nearly constant time shift of about 6 μs. This is especially true for the BRL model. This time shift corresponds to a mean electron velocity around 33 km/s. As can be seen in Fig. 7, the three models give different density values. As previously explained, the ABR model tends to underestimate the density. The maximum electron density measured on the VAT axis 20 cm downstream of the anode is then n_e,max ≈ 8×10¹⁷ m ⁻³.

Electron temperature

Figure 8 shows the temporal evolution of the electron temperature T_e during a VAT current pulse. The activation of the triggering system is clearly identified in Fig. 8, which means this short phase has a considerable influence on the plasma and jet properties. As a matter of fact a peak in the temperature time series is observed around 7 μs with an electron temperature in excess of 25 eV.

Fig. 8

Time evolution of the electron temperature at x=20 cm. The solid line is the discharge current trace

The group of high-temperature electrons is also observed in Fig. 5. A small current peak is for instance visible around 7 μs even when the probe is polarized at -15 V. It means some electrons have enough energy to go beyond the potential barrier. They also are numerous enough to counterbalance the charge of the ions arriving at the same time. The occurrence of this high-temperature peak is of course a direct consequence of the very high voltage applied to the VAT electrodes during the trigger phase. A large amount of energy is injected into the discharge at the beginning of the pulse as voltage applied to the trigger electrode is much larger than the one applied to the anode. Two other temperature peaks are observed in the time series around 16 μs and 24 μs respectively, see Fig. 8. The two peaks have a relatively low amplitude as the maximum temperature is about 7 eV.

It is known that the cathode spots, therefore the arcs, have a complex and rich dynamics. They migrate on the cathode surface in a stochastic way both with and without the application of an external magnetic field [23,24,25,26,27]. They can also fade away and then quickly appear again somewhere else on the cathode surface. Therefore the electron temperature time evolution certainly images to a large extent the cathode spot and arc behavior. The first peak could corresponds to the discharge creation and the first arc formation. The two other peaks in Fig. 8 would then indicate the generation of two secondary arcs delayed in time.

Plasma potential

The time evolution of the plasma potential V_p is shown in Fig. 9. The voltage resolution is rather low in this graph since the step size is 1 V in our I-V curve acquisition method. As expected, there are striking similarities between the temporal evolution of the plasma potential and the temporal evolution of the electron temperature.

Fig. 9

Time evolution of the plasma potential at x=20 cm. The solid line is the discharge current trace

A peak value is reached at 7 μs during the trigger phase. The plasma potential is then around 26 V. Two other peaks with a lower intensity around 14 V are visible at 16 μs and 24 μs in Fig. 9, in agreement with the temperature time evolution. As previously explained, the shape of the V_p temporal profile is related to the cathode arc formation and motion on the cathode surface.

Ion properties

Velocity

An estimate of the ion velocities can be determined by the time-of-flight (ToF) method that measures to time it takes for ions to travel a given distance. In this work a planar probe is used to detect ion arrival downstream of the anode after they have traveled 17.5 cm. Notice the ToF technique makes no assumption on the ion electrical charge state. Figure 4 shows typical ion current waveforms acquired with the probe during a current pulse. Although very simple, this ToF technique suffers from the fact that the moment ions are created and leave the cathode remains unknown. We therefore assume that all ions are created at discharge ignition when the capacitor bank starts releasing energy. This moment has been used as the time reference for analyzing all data here, see “Traces and Time evolution of electron parameters” sections. This assumption is very strong and contradicts preceding analysis that relies upon the presence of several electron and ion populations produced or ejected at different moments in time. This assumption is nevertheless the most reasonable not to introduce very large error bars in the velocity values. Moreover, it provides for sure the lowest velocity ion can have.

Ion current traces displayed in Fig. 4 allow an estimation of the velocity. Using the orange trace termed “Pulse 2” in the figure, the first peak gives an ion velocity v₁=17.0 km/s while the second peak gives a velocity v₂=9.5 km/s. These values are in good agreement with ones obtained in other works on VAT, see e.g. [3, 28, 29]. In the remainder of the paper we will solely consider the first large peak on the ion current traces as the origin of other peaks is questionable. Figure 10 shows the statistical distribution of the velocity determined by ToF from the first current peak. This distribution was contructed from the recording of 42 traces with a planar probe polarized at -50 V. The mean velocity amounts to 20.1 km/s with a standard deviation of 3.1 km/s. In Fig. 10, ion velocities spread from 14.5 km/s to more than 28 km/s, which is consistent with the values usually found in the literature [3, 28, 29]. Again the large velocity spread reveals the stochastic character of the arc formation. Moreover, it indicates that the thrust generated by the PJP is most probably not the same from one pulse to an other, as it depends (among other things) on the ion velocity.

Fig. 10

Velocity distribution of the first ion population

Mean charge

Combining all data, one can compute the evolution in time of the ion mean electrical charge. The relation between the ion current density j_i, the plasma density n_e, the ion velocity v_i and the mean charge Q reads:

$$j_{i}= n_{e} v_{i} e Q,$$

(1)

where e the elementary charge. The plasma is here assumed to be quasi-neutral with n_e=n_i. This assumption is certainly reasonable far away from the cathode, i.e in the far-field plume [30, 31]. The current density was measured with a Faraday probe, the electron density was inferred from Langmuir probe measurements and the ion velocity is obtained by the ToF technique. When ions hit the probe at time t, their velocity v_i is considered to be 0.2/t. This implies that all ions are created at the same moment, but that the different ion populations have a different velocity. All measurements were averaged over 200 discharge current pulses. The time evolution of the ion mean charge state 20 cm away from the anode plane is shown in Fig. 11.

Fig. 11

Ion mean charge as a function of time at x=20 cm. The solid line is the discharge current trace

During the trigger phase the mean charge is very large with Q above 12+. The plasma created at ignition is in vacuum spark regime, which is characterized by a high voltage and a short duration. It is know that in this specific regime ions can reach a very high charge state [32]. In the case of high current sparks, the self-induced magnetic field pinches and heats the plasma. Instabilities and contractions develop in regions of pinch, which leads to the formation of highly charged ions [33]. Ions with charge state above 10+ have indeed been observed [34]. Beyond 10 μs the plasma reaches the vacuum arc regime, which is characterized by a lower voltage and a relatively steady state. A constant mean charge around 2+ is reached in the jet during this regime, as can be seen in Fig. 11. This is in agreement with values published in the literature [35].

The thrust level is obviously a relevant parameter for propulsion purposes. Using the mean ion charge, one can compute the instantaneous thrust on the VAT axis. The thrust is related to the ion charge according to the following equation:

$$T= \dot{m_{i}} v_{i} = \frac{I_{i}}{eQ}m v_{i}$$

(2)

where $\dot {m_{i}}$ is the ion mass flow rate, I_i is the ion current and m the atom mass. As the cathode is composed of Nickel (80 %) and Chromium (20 %), the average mass is here m=57.3 amu. The time evolution of the on-axis thrust T is shown in Fig. 12 along with the ion current trace averaged over 200 pulses.

Fig. 12

Instantaneous on-axis thrust determined at x=20 cm (symbol). Trace of the ion current measured by a Faraday cup (line)

The plot in Fig. 12 is not intended to give the thrust level of the PJP thruster as a function of time. Instead it can be used to investigate the impact of the various parameters on thrust generation. It can be noticed that the thrust is larger and almost constant after the trigger phase. Thrust generation would therefore be dominated by the arc regime. Said differently, ions with a low charge contribute more to the thrust than highly-charged ions produced at the very beginning of the current pulse.

Conclusion

Electron and ion current measurements have been carried out in the plume of the 30-W class PJP vacuum arc thruster equipped with a Ni/Cr cathode. Whereas the discharge current trace is smooth and well described by a Weibull-type function, measurements performed 20 cm downstream of the anode plane reveal the complexity of the phenomena involved.

Time-resolved electrostatic probe measurements in the jet give new insights into the electrons and ions dynamics in a pulsed high-current low-power VAT. The high-voltage discharge triggering produces a vacuum spark containing hot electrons with T_e above 25 eV as well as highly charged ions as the electrical charge reaches up to 12+. After ignition, the vacuum arc operates in a relatively stable regime for more than 25 μs with a maximum electron density that amounts to about 10¹⁸ m ⁻³ on the thruster axis. Surprisingly, it turns out that the generated thrust is the highest in the arc regime despite the presence of highly charged ions in the spark.

Time- and spatially-resolved plasma properties measurements will be performed in next campaigns with an upgraded version of our diagnostic tool set. Moreover, the impact of the cathode material on the plasma discharge and jet properties will also be investigated. Additional and new experimental results, combined with numerical simulations outcomes, will certainly improve the understanding of pulsed high-current vacuum arc thruster physics, which in turn will allow improvement of the overall performances.