Predictive Estimation of Finite Population Mean in Case of Missing Data Under Two-phase Sampling

Abstract

The present paper deals with the problem of estimation of finite population mean of study variable using two auxiliary variables in two-phase sampling scheme using predictive approach in case of missing values of the study variable and unknown population mean of first auxiliary variable. Four classes of such estimators have been proposed using this predictive approach. The expressions of bias and mean square errors are derived up to first order of approximation. The optimal values of the constants involved in the proposed classes of estimators have been obtained and thus minimum mean square errors of the proposed classes are obtained in this study. The empirical and graphical comparisons with regression type estimators (under single phase and double phase sampling scheme) and also among themselves have been made for evaluating the performance of the proposed classes for different choices of non-responding units. Five real data sets and three simulated data sets following normal distribution have been used to evaluate the performance of the proposed classes. Numerical findings confirm the theoretical results obtained regarding superiority of proposed classes of estimators over the conventional regression type estimators in terms of percent relative efficiencies.

1 Introduction

Data missingness has grown to be a significant issue for practitioners, and understanding its stochastic character is crucial to understand the strategies that should be used to address the issue of incomplete data. In medical and social sciences, collecting, analyzing and drawing inferences from data is crucial for research. Missing data can seriously affect inferences from randomized clinical trials, if missing data are not handled properly. Hansen and Hurwitz [1] first introduced how to deal with the problem of incomplete samples in mail surveys. Further, Rubin [2] gave detailed description of the concepts: Missing at Random (MAR), Observed at Random (OAR), Missing Completely at Random (MCAR) and Parameter Distinctness (PD). Researchers have developed a variety of imputation strategies over the years so that samples are structurally complete and analyses may be performed successfully. These techniques fill in missing values with an appropriate function of the given data. Sande [3] and Kalton et al. [4] suggested imputation methods that make an incomplete data set structurally complete. Mean imputation, ratio imputation, regression imputation, hot deck imputation, cold deck imputation, and nearest neighbor imputation, etc. are some popular imputation techniques. Researchers have made continuous efforts to devise improved estimators of population mean of the study variable by developing efficient imputation techniques which include ref. [5,6,7,8,9,10,11,12,13] and many more. In the survey sample literature, numerous authors have taken non-response scenarios into account when estimating the population variance of the study variable such as Singh and Joarder [14], Sharma [15], Singh et al. [16], Singh and Khalid [17], Sharma and Singh [18], Singh et al. [19], Basit and Bhatti [20], and Singh and Khalid [21].

Auxiliary information is frequently used in survey sample situations to increase the accuracy of an estimator, whether at the planning stage, or the designing stage, or the estimate stage, or a combination of these phases. When complete information on auxiliary variable is available, then ratio, regression, and conventional imputation techniques can be utilized to anticipate the information on population mean of the study variable. But, if the information of the population mean of the auxiliary variable is not available, then two phase sampling scheme is employed. Chand [22] suggested a method of chaining the information on first and second auxiliary variables correlated with the study variable which was further extended by many authors like, Kiregyera [23, 24], Srivastava [25], Singh et al. [26], Gupta and Shabbir [27], Chaudhary and Singh [28], Kumar and Sharma [29], Mehta and Tailor [30] and many more.

Basu [31] gave a predictive approach and used it to predict, non-sampled values which was further advocated by many researchers to use existing estimators as predictors in different types of statistical models. In this direction, major contributions are Sahoo and Panda [32], Sahoo and Sahoo [33], Sahoo et al. [34], Saini [35], Singh et al. [36], Singh and Singh [37], Yadav and Mishra [38], Bandyopadhyay and Singh [39], Singh et al. [40], Kumar and Saini [41] and many more, who gave enhanced efficient predictive estimators of finite population mean. Till now, no predictive approach has been applied when complete data of study variable is not available. Motivated and encouraged by the recent work of all above authors using predictive approach in case of complete data, we propose different classes of estimators of population mean under predictive approach (in double sampling scheme using two auxiliary variables) when observations on the variable of interest are missing and population mean of first auxiliary variable is unknown. We have applied four different methods of imputation to propose our four different classes of estimators of population mean in Sect. 4.

2 Methodology and Notations

Let $\mathcal{U}$ = $\left\{{U}_{1},{U}_{2}, . . . ,{U}_{N}\right\}$ be a finite population consisting of N identifiable units. Suppose Y, X, and Z, be the character under study (whose mean $\overline{Y}$ is to be estimated), first and second auxiliary variables, respectively. Here, Y is assumed to be positively correlated with both X and Z, while its correlation with X is stronger than its correlation with Z. In addition, we suppose that the population mean of X is unknown, but the population mean of Z is available in advance. Let $\left({Y}_{i}, {X}_{i},{Z}_{i}\right)$ be the value of variable $\left(Y,X,Z\right)$ for the i^th unit of population.

Let a first phase sample $S^{'}$ of size $n^{'}$ be drawn (using simple random sampling without replacement (SRSWOR)) from the population $.$ Let $\mathcal{S}$ be the second phase sample selected from first phase sample of size n $\left(<n^{'}\right).$ On these n units, the information of variables Y, X and Z have been measured. Suppose information on r units corresponding to variable Y is obtained but on the remaining $\left(n-r\right)$ units, information is missing. Also, it is assumed that information of variables X and Z is available on all these $n$ units. Let the responding set of sampling units be denoted by R and that of non-responding set by${R}^{c}$. So, $\mathcal{S}$= R $\cup {R}^{c}.$ For each i $\in$ R, value of the sampling observation y_i is known. However, for the units i$\in {R}^{c}$, the sampling observation y_i values are missing and thus for these imputed values have to be derived.

The following notations are used throughout the paper:

$\overline{Y }, \bar{X}, \overline{Z }$: population means of the study variable, first, and second auxiliary variable respectively.

${\overline{y} }_{r}, { \overline{x} }_{r}, {\overline{x} }_{n},{ \overline{z} }_{n},{ \overline{x} }_{n^{'}},{ \overline{z} }_{n^{'}}:$ sample means of the respective variables for the sample sizes shown in suffices.

${\rho }_{yx}, {\rho }_{yz},{ \rho }_{xz} :$ correlation coefficients between the variables as shown in subscripts for the whole population.

${\beta }_{yx}, {\beta }_{yz}, { \beta }_{xz}$: Population regression coefficients of the variables shown in subscripts.

${b}_{yx}(r)$: Sample regression coefficient between y and x based on the sample of size r.

${S}_{y}^{2},{S}_{x}^{2} ,:$ Population variances (with divisors $\left(N-1\right)$) of the variables Y, X and Z respectively.

${S}_{yx}, { S}_{yz}, {S}_{xz}:$ Population covariances (with divisors $\left(N-1\right))$ between the variables as shown in subscripts.

${C}_{y}$, ${C}_{x}, { C}_{z}$: Coefficients of variation of the variables as shown in subscripts.

${s}_{yx}\left(r\right):$ Sample covariance (with divisors $\left(r-1\right)$) between y and x based on the sample of size r.

${s}_{x}^{2}\left(r\right):$ Sample variance (with divisors $\left(r-1\right)$) of the variable x based on the sample of size r.

Also for the sake of simplicity define, ${\lambda }_{1}=\frac{1}{n}-\frac{1}{N}$, ${\lambda }_{2}=\frac{1}{r}-\frac{1}{N}$, ${\lambda }_{3}=\frac{1}{n^{'}}-\frac{1}{N}$.

In the following section, we have mentioned some existing imputation techniques when the population mean $\overline{X }$ is unknown and in the absence of second auxiliary variable $Z$. The corresponding point estimators of $\overline{Y }$, and their variances or minimum mean square error are mentioned which shall be later used for the comparison purposes.

3 Some Traditional Imputation Methods

In this section, some traditional methods of imputation are given considering single and double sampling strategy, assuming that $\overline{X }$ is unknown, by replacing $\overline{X }$ with ${\overline{x} }_{n^{'}}$.

(i) Simple mean method of imputation (under single phase sampling scheme).

The imputation scheme under simple mean method of imputation is:

$${y}_{.i}=\left\{\begin{array}{c}{y}_{i} \quad i\in R \\ {\overline{y} }_{r } \quad i\in {R}^{c}\\ \end{array}\right.$$

The corresponding point estimator for $\overline{Y }$ is:

$${\overline{y} }_{m}={\overline{y} }_{r}$$

The variance of this estimator is:

$Var({\overline{y} }_{m})= \left(\frac{1}{r}-\frac{1}{N}\right){\overline{Y} }^{2}{{C}_{y}}^{2}$

(ii) Ratio method of imputation (under single phase sampling scheme).

The imputation scheme under ratio method of imputation is

$${y}_{.i}=\left\{\begin{array}{c}{y}_{i}\quad i\in R \\ \widehat{a}{x}_{i}\quad i\in {R}^{c}\\ \end{array}\right.$$

where $\widehat{a}= \frac{\sum_{i\in R}{y}_{i}}{\sum_{i\in R}{x}_{i}}$

The corresponding point estimator for $\overline{Y }$ is:

$${\overline{y} }_{Rat}= {\overline{y} }_{r}\frac{{\overline{x} }_{n}}{{\overline{x} }_{r}}$$

The Mean Square Error ($MSE)$ of this estimator is:

$${MSE\left({\overline{y} }_{Rat}\right)=\overline{Y} }^{2}\left(\left(\frac{1}{r}-\frac{1}{N}\right){{C}_{y}}^{2}+\left(\frac{1}{r}-\frac{1}{n}\right)({C}_{x}^{2}-2{\rho }_{yx}{C}_{y}{C}_{x})\right)$$

(iii) Compromised Method of Imputation (Singh and Horn [42]) (under single phase sampling scheme).

The imputation scheme under compromised method of imputation is:

$${y}_{COMP}=\left\{\begin{array}{cc}{y}_{i}& i\in R\\ \frac{1}{n-r}\left[n\left({\alpha \overline{y} }_{r}+{\left(1-\alpha \right)\overline{y} }_{r}\left(\frac{{\overline{x} }_{n}}{{\overline{x} }_{r}}\right)\right)-r{\overline{y} }_{r}\right]& i\in {R}^{c}\end{array}\right.$$

where $\alpha$ is a constant chosen suitably.

The corresponding point estimator for $\overline{Y }$ is:

$${\overline{y} }_{COMP}={\alpha \overline{y} }_{r}+{\left(1-\alpha \right)\overline{y} }_{r}\left(\frac{{\overline{x} }_{n}}{{\overline{x} }_{r}}\right)$$

The $MSE$ of the estimator is derived as:

$${{MSE}_{min}\left({\overline{y} }_{COMP}\right)=\overline{Y} }^{2}\left(\left(\frac{1}{n}-\frac{1}{N}\right){{C}_{y}}^{2}+\left(\frac{1}{r}-\frac{1}{n}\right)(1-{\rho }_{yx}^{2}){{C}_{y}}^{2}\right)$$

(iv) Regression method of imputation (under single phase sampling scheme).

The imputation scheme under regression method of imputation is:

$${y}_{.i}=\left\{\begin{array}{c}{y}_{i}\quad i\in R \\ \widehat{c}+{\widehat{b}}_{yx}{x}_{i}\quad i\in {R}^{c}\\ \end{array}\right.$$

where ${\widehat{b}}_{yx}=\frac{{s}_{yx}(r)}{{s}_{x}^{2}\left(r\right)}$ and $\widehat{c}=\left({\overline{y} }_{r}-{\widehat{b}}_{yx}{\overline{x} }_{r}\right)$.

The corresponding point estimator for $\overline{Y }$ is:

$${\overline{y} }_{reg1}={\overline{y} }_{r}+{\widehat{b}}_{yx}\left({\overline{x} }_{n}-{\overline{x} }_{r}\right)$$

and $MSE$ is as follows:

$${MSE\left({\overline{y} }_{reg1}\right)=\overline{Y} }^{2}{{C}_{y}}^{2}\left(\left(\frac{1}{n}-\frac{1}{N}\right)+\left(\frac{1}{r}-\frac{1}{n}\right)(1-{\rho }_{yx}^{2})\right)$$

(v) Regression method of imputation (under double sampling scheme).

The corresponding point estimator for $\overline{Y }$ is:

$${\overline{y} }_{reg2}={\overline{y} }_{r}+{\widehat{b}}_{yx}\left({\overline{x} }_{n^{'}}-{\overline{x} }_{r}\right)$$

The $MSE$ is obtained as:

$${MSE\left({\overline{y} }_{reg2}\right)=\lambda }_{2}{\overline{Y} }^{2}{C}_{y}^{2}+\left({\lambda }_{3}-{\lambda }_{2}\right){\overline{Y} }^{2}{\rho }_{yx}^{2}{C}_{y}^{2}$$

A number of authors have developed estimators of $\overline{Y }$ in case of missing data, considering two phase sampling scheme, replacing ${\overline{x} }_{n^{'}}$ by an improved estimator of $\overline{X }$ when there exists another auxiliary variable Z. In the following section, we propose some new efficient classes of estimators of $\overline{Y }$ using predictive approach advocated by Basu [31], when X and Z, two auxiliary variables are present.

4 Proposed Classes of Estimators Under Predictive Approach

To build up estimators of $\overline{Y }$, we represent $\overline{Y }$ as

$$\overline{Y }= \frac{1}{N}\left(\sum_{i\in R}{y}_{i}+\sum_{i\in {R}_{1}}{y}_{i}+\sum_{i\in {R}_{2}}{y}_{i}+\sum_{i\in {R}_{3}}{y}_{i}\right),$$

by decomposing the population U into four mutually exclusive domains: R, ${R}_{1}=S-R,$ ${R}_{2}=S^{'}-S$ and ${R}_{3}=S^{'^{c}}$ of $r, (n-r),(n^{'}-n),$ and $\left(N-n^{'}\right)$ units, respectively. Writing $\left(n-r\right){\overline{y} }_{1}= \sum_{i\in {R}_{1}}{y}_{i}$, $\left(n^{'}-n\right){\overline{y} }_{2}= \sum_{i\in {R}_{2}}{y}_{i}$, and $\left(N-n^{'}\right){\overline{y} }_{3}= \sum_{i\in {R}_{3}}{y}_{i}$. Thus, we have

$$\overline{Y }= {p}_{1}{\overline{y} }_{r}+\left({p}_{2}-{p}_{1}\right){\overline{y} }_{1}+\left({p}_{3}-{p}_{2}\right){\overline{y} }_{2}+ \left(1-{p}_{3}\right){\overline{y} }_{3},$$

(1)

where${p}_{1}=\frac{r}{N}$,${p}_{2}=\frac{n}{N}$, ${p}_{3}=\frac{n^{'}}{N}$. Since the right-hand side of (1)'s first term is known, so the problem is to predict the quantities${\overline{y} }_{1}$, ${\overline{y} }_{2}$, and ${\overline{y} }_{3}$ from the sampled data. If${T}_{1}$, ${T}_{2}$ and ${T}_{3}$ are respectively their inferred predictors, then under predictive approach, an estimator of $\overline{Y }$ is given as:

$$\widehat{\overline{Y} }= {p}_{1}{\overline{y} }_{r}+\left({p}_{2}-{p}_{1}\right){T}_{1}+\left({p}_{3}-{p}_{2}\right){T}_{2}+ \left(1-{p}_{3}\right){T}_{3}$$

(2)

In case of no additional auxiliary data on population is available, then the simplest option for ${T}_{1},{T}_{2},{T}_{3}$ would be ${\overline{y} }_{r}$, which gives $\widehat{\overline{Y} }=$ ${\overline{y} }_{r}$. But the goal of this study is to propose efficient estimators (or classes of estimators) of $\overline{Y }$ using predictive approach when two auxiliary variables X and Z are present.

Since data on X is known at the sample level, so we predict Y-values in the domains ${R}_{1}$ and ${R}_{2}$ using X-values only. By taking ${T}_{1}={\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and ${T}_{2}={\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n}\right)$, where $\left(n-r\right){\overline{X} }_{1}=$ $\sum_{i\in {R}_{1}}{x}_{i}$ and $\left(n^{'}-n\right){\overline{X} }_{2}= \sum_{i\in {R}_{2}}{x}_{i}$, where ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and ${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n}\right)$ are functions of $\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and $\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n}\right)$ such that.

${\varphi }_{1}\left(\overline{Y },\overline{X}, \overline{X }\right)$= $\overline{Y }\Rightarrow{\left(\frac{\partial \left( {\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r} \right)\right)}{\partial {\overline{y} }_{r}}\right)}_{\left(\overline{Y },\overline{X}, \overline{X }\right)}=1$ and.

${\varphi }_{2}\left(\overline{Y },\overline{X}, \overline{X }\right)$= $\overline{Y }\Rightarrow{\left(\frac{\partial \left( {\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right)\right)}{\partial {\overline{y} }_{r}}\right)}_{\left(\overline{Y },\overline{X}, \overline{X }\right)}=1,$ respectively.

They also satisfying certain regularity conditions like:

1. Whatever be the sample chosen, the sample point $\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ assumes values in a bounded, closed convex subset, P, of ${R}^{3}$ containing the point $\left(\overline{Y },\overline{X}, \overline{X }\right).$

2. The function ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ is continous and bounded in P.

3. The third order partial derivatives of ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ exist and are continous and bounded in P.

The similar regularity conditions are also assumed for sample point $\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right)$ and the function ${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n}\right)$.

The expansions of ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and ${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right)$ about the point $\left(\overline{Y },\overline{X}, \overline{X }\right)$ using Taylor’s series up to second order (neglecting remainder terms), give the following expressions:

$${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r} \right)=\overline{Y }+{h}_{1}\left({\overline{y} }_{r}-\overline{Y }\right)+{h}_{2}\left({\overline{X} }_{1}-\overline{X }\right)+{h}_{3}\left({\overline{x} }_{r}-\overline{X }\right)+ \frac{1}{2!}\left[{h}_{11}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}{\left({\overline{X} }_{1}-\overline{X }\right)}^{2}+{h}_{33}{\left({\overline{x} }_{r}-\overline{X }\right)}^{2}+2{h}_{12}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{1}-\overline{X }\right)+2{h}_{23}\left({\overline{X} }_{1}-\overline{X }\right)\left({\overline{x} }_{r}-\overline{X }\right)+2{h}_{13}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{r}-\overline{X }\right)\right]$$

and

$${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right)=\overline{Y }+{h}_{1}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)+{h}_{2}^{'}\left({\overline{X} }_{2}-\overline{X }\right)+{h}_{3}^{'}\left({\overline{x} }_{n}-\overline{X }\right)+\frac{1}{2!}\left[{h}_{11}^{'}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{'}{\left({\overline{X} }_{2}-\overline{X }\right)}^{2}+{h}_{33}^{'}{\left({\overline{x} }_{n}-\overline{X }\right)}^{2}+2{h}_{12}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{2}-\overline{X }\right)+2{h}_{23}^{'}\left({\overline{X} }_{2}-\overline{X }\right)\left({\overline{x} }_{n}-\overline{X }\right)+2{h}_{13}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{n}-\overline{X }\right)\right]$$

where ${h}_{i}, {h}_{i}^{'}$ are the first order partial derivatives and ${h}_{ij}, {h}_{ij}^{'}$ are second order partial derivatives of ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and ${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right) (i=\mathrm{1,2},3;j=\mathrm{1,2},3)$ respectively at the point $\left(\overline{Y },\overline{X}, \overline{X }\right).$ Also, ${h}_{1}={h}_{1}^{'}=1, {h}_{2}=-{h}_{3}, {h}_{2}^{'}=-{h}_{3}^{'}$, ${h}_{11}={h}_{11}^{'}=0$.

Since, information on Z is available at the population level, so we make four different selections for ${T}_{3}$ and thus obtained four different estimators for $\overline{Y },$ using result (2).

(i) Let ${T}_{3}=$ ${\overline{y} }_{r}\frac{{\overline{Z} }_{3}}{{\overline{z} }_{{n}{\prime}}}$ then from (2), $\widehat{\overline{Y}}$ comes out to be.

${\widehat{\overline{Y}} }_{1}=$ ${p}_{2}{h}_{2}\left({\overline{x} }_{n}-{\overline{x} }_{r}\right)+ {p}_{3}{h}_{2}^{'}\left({\overline{x} }_{{n}^{'}}-{\overline{x} }_{n}\right)$+ ${\overline{y} }_{r}\frac{\overline{Z} }{{\overline{z} }_{{n}{\prime}}}$  + (${p}_{2}-{p}_{1}) \frac{1}{2!}\left[{h}_{11}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}{\left({\overline{X} }_{1}-\overline{X }\right)}^{2}+{h}_{33}{\left({\overline{x} }_{r}-\overline{X }\right)}^{2}+2{h}_{12}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{1}-\overline{X }\right)+2{h}_{23}\left({\overline{X} }_{1}-\overline{X }\right)\left({\overline{x} }_{r}-\overline{X }\right)+2{h}_{13}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{r}-\overline{X }\right)\right]+({p}_{3}-{p}_{2})\frac{1}{2!}\left[{h}_{11}^{'}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{'}{\left({\overline{X} }_{2}-\overline{X }\right)}^{2}+{h}_{33}^{'}{\left({\overline{x} }_{n}-\overline{X }\right)}^{2}+2{h}_{12}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{2}-\overline{X }\right)+2{h}_{23}^{'}\left({\overline{X} }_{2}-\overline{X }\right)\left({\overline{x} }_{n}-\overline{X }\right)+2{h}_{13}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{n}-\overline{X }\right)\right]$, where $\left({N-n^{'}}\right){\overline{Z} }_{3}= \sum_{i\in {R}_{3}}{z}_{i}$,

(ii) Let ${T}_{3}=$ ${\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n^{'}}}\right)$, where ${\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n^{'}}}\right)$ is a function of $\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n^{'}}}\right)$ such that

$$\left( {\overline {Y},\overline {Z}, \overline Z} \right) = \bar Y \Rightarrow {\left( {\frac{{\partial \left( {{\varphi _3}\left( {{{\bar y}_r},{{\bar Z}_3},{{\bar z}_{n^{'} }}} \right)} \right)}}{{\partial {{\bar y}_r}}}} \right)_{\left( {\overline {Y},\overline {Z}, \overline Z} \right)}} = 1,$$

and satisfying certain regularity conditions similar to functions ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r}\right)$ and ${\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n}\right)$.

The expansion of ${\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n}{\prime}}\right)$ about the point $\left(\overline{Y },\overline{Z}, \overline{Z }\right)$ in second order Taylor’s series neglecting remainder terms, gives the following expression:

$${\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n}^{'}}\right)=\overline{Y }+{h}_{1}^{{\prime}{\prime}}\left({\overline{y} }_{r}-\overline{Y }\right)+{h}_{2}^{{\prime}{\prime}}\left({\overline{Z} }_{3}-\overline{Z }\right)+{h}_{3}^{{\prime}{\prime}}\left({\overline{z} }_{{n}^{'}}-\overline{Z }\right)+\frac{1}{2!}\left[{h}_{11}^{{\prime}{\prime}}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{{\prime}{\prime}}{\left({\overline{Z} }_{3}-\overline{Z }\right)}^{2}+{h}_{33}^{{\prime}{\prime}}{\left({\overline{z} }_{{n^{'}}}-\overline{Z }\right)}^{2}+2{h}_{12}^{{\prime}{\prime}}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{Z} }_{3}-\overline{Z }\right)+2{h}_{23}^{{\prime}{\prime}}\left({\overline{Z} }_{3}-\overline{Z }\right)\left({\overline{z} }_{{n^{'}}}-\overline{Z }\right)+2{h}_{13}^{{\prime}{\prime}}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{z} }_{{n^{'}}}-\overline{Z }\right)\right]$$

where ${h}_{i}^{{\prime}{\prime}}$ are the first order partial derivatives and ${h}_{ij}^{{\prime}{\prime}}$ are second order partial derivatives of ${\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n^{'}}}\right) (i=\mathrm{1,2},3, j=\mathrm{1,2},3)$ at the point $\left(\overline{Y }, \overline{Z }, \overline{Z }\right).$ Also, ${h}_{1}^{{\prime}{\prime}}=1, {h}_{2}^{{\prime}{\prime}}=-{h}_{3}^{{\prime}{\prime}}$, ${h}_{11}^{{\prime}{\prime}}=0$.

Then from (2), $\widehat{\overline{Y} }$ comes out to be.

${\widehat{\overline{Y}} }_{2}={{\overline{y} }_{r}+{h}_{2}p}_{2}\left({\overline{x} }_{n}-{\overline{x} }_{r}\right)+ {h}_{2}^{'}{p}_{3}\left({\overline{x} }_{{n^{'}}}-{\overline{x} }_{n}\right)+{h}_{2}^{{\prime}{\prime}}\left(\overline{Z }-{\overline{z} }_{{n^{'}}}\right)+$$({p}_{2}-{p}_{1}) \frac{1}{2!}\left[{h}_{11}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}{\left({\overline{X} }_{1}-\overline{X }\right)}^{2}+{h}_{33}{\left({\overline{x} }_{r}-\overline{X }\right)}^{2}+2{h}_{12}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{1}-\overline{X }\right)+2{h}_{23}\left({\overline{X} }_{1}-\overline{X }\right)\left({\overline{x} }_{r}-\overline{X }\right)+2{h}_{13}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{r}-\overline{X }\right)\right]+({p}_{3}-{p}_{2})\frac{1}{2!}\left[{h}_{11}^{'}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{'}{\left({\overline{X} }_{2}-\overline{X }\right)}^{2}+{h}_{33}^{'}{\left({\overline{x} }_{n}-\overline{X }\right)}^{2}+2{h}_{12}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{2}-\overline{X }\right)+2{h}_{23}^{'}\left({\overline{X} }_{2}-\overline{X }\right)\left({\overline{x} }_{n}-\overline{X }\right)+2{h}_{13}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{n}-\overline{X }\right)\right]+(1-{p}_{3})\frac{1}{2!}\left[{h}_{11}^{{\prime}{\prime}}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{{\prime}{\prime}}{\left({\overline{Z} }_{3}-\overline{Z }\right)}^{2}+{h}_{33}^{{\prime}{\prime}}{\left({\overline{z} }_{{n}{\prime}}-\overline{Z }\right)}^{2}+2{h}_{12}^{{\prime}{\prime}}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{Z} }_{3}-\overline{Z }\right)+2{h}_{23}^{{\prime}{\prime}}\left({\overline{Z} }_{3}-\overline{Z }\right)\left({\overline{z} }_{{n^{'}}}-\overline{Z }\right)+2{h}_{13}^{{\prime}{\prime}}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{z} }_{{n^{'}}}-\overline{Z }\right)\right]$.

(iii) Let ${T}_{3}={k}_{1}{\overline{y} }_{r}+{k}_{2}\left({\overline{Z} }_{3}-{\overline{z} }_{{n^{'}}}\right)$, then from (2), $\widehat{\overline{Y} }$ comes out to be.

${\widehat{\overline{Y}} }_{3}={{[{k}_{1}\left(1-{p}_{3}\right)+{p}_{3}]\overline{y} }_{r}+{h}_{2}p}_{2}\left({\overline{x} }_{n}-{\overline{x} }_{r}\right)+ {{h}_{2}^{'}p}_{3}\left({\overline{x} }_{{n^{'}}}-{\overline{x} }_{n}\right)+{k}_{2}\left(\overline{Z }-{\overline{z} }_{{n^{'}}}\right)+({p}_{2}-{p}_{1}) \frac{1}{2!}\left[{h}_{11}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}{\left({\overline{X} }_{1}-\overline{X }\right)}^{2}+{h}_{33}{\left({\overline{x} }_{r}-\overline{X }\right)}^{2}+2{h}_{12}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{1}-\overline{X }\right)+2{h}_{23}\left({\overline{X} }_{1}-\overline{X }\right)\left({\overline{x} }_{r}-\overline{X }\right)+2{h}_{13}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{r}-\overline{X }\right)\right]+({p}_{3}-{p}_{2})\frac{1}{2!}\left[{h}_{11}^{'}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{'}{\left({\overline{X} }_{2}-\overline{X }\right)}^{2}+{h}_{33}^{'}{\left({\overline{x} }_{n}-\overline{X }\right)}^{2}+2{h}_{12}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{2}-\overline{X }\right)+2{h}_{23}^{'}\left({\overline{X} }_{2}-\overline{X }\right)\left({\overline{x} }_{n}-\overline{X }\right)+2{h}_{13}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{n}-\overline{X }\right)\right]$.

(iv) Let ${T}_{3}={[k}_{1}{\overline{y} }_{r}+{k}_{2}\left({\overline{Z} }_{3}-{\overline{z} }_{{n^{'}}}\right)]exp\left(\frac{{\overline{Z} }_{3}-{\overline{z} }_{{n^{'}}}}{{\overline{Z} }_{3}+{\overline{z} }_{{n^{'}}}}\right)$, then from (2), $\widehat{\overline{Y} }$ comes out to be

$${\widehat{\overline{Y}} }_{4}={{[{p}_{3}+{k}_{1}\left(1-{p}_{3}\right)exp\left(\frac{{\overline{Z} }_{4}-{\overline{z} }_{{n^{'}}}}{{\overline{Z} }_{4}+{\overline{z} }_{{n^{'}}}}\right)]\bar{y}_{r}}+h_{2}p_{2}}\left({\overline{x} }_{n}-{\overline{x} }_{r}\right)+ {{h}_{2}^{'}p}_{3}\left({\overline{x} }_{{n^{'}}}-{\overline{x} }_{n}\right)+{k}_{2}\left(\overline{Z }-{\overline{z} }_{{n^{'}}}\right)exp\left(\frac{{\overline{Z} }_{3}-{\overline{z} }_{{n^{'}}}}{{\overline{Z} }_{3}+{\overline{z} }_{{n^{'}}}}\right)+\left({p}_{2}-{p}_{1}\right)\frac{1}{2!}\left[{h}_{11}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}{\left({\overline{X} }_{1}-\overline{X }\right)}^{2}+{h}_{33}{\left({\overline{x} }_{r}-\overline{X }\right)}^{2}+2{h}_{12}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{1}-\overline{X }\right)+2{h}_{23}\left({\overline{X} }_{1}-\overline{X }\right)\left({\overline{x} }_{r}-\overline{X }\right)+2{h}_{13}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{r}-\overline{X }\right)\right]+\left({p}_{3}-{p}_{2}\right)\frac{1}{2!}\left[{h}_{11}^{'}{\left({\overline{y} }_{r}-\overline{Y }\right)}^{2}+{h}_{22}^{'}{\left({\overline{X} }_{2}-\overline{X }\right)}^{2}+{h}_{33}^{'}{\left({\overline{x} }_{n}-\overline{X }\right)}^{2}+2{h}_{12}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{X} }_{2}-\overline{X }\right)+2{h}_{23}^{'}\left({\overline{X} }_{2}-\overline{X }\right)\left({\overline{x} }_{n}-\overline{X }\right)+2{h}_{13}^{'}\left({\overline{y} }_{r}-\overline{Y }\right)\left({\overline{x} }_{n}-\overline{X }\right)\right].$$

Remark 4.1

It may be noted that the selection of predictors ${\varphi }_{1}\left({\overline{y} }_{r}, {\overline{X} }_{1},{\overline{x} }_{r} \right), {\varphi }_{2}\left({\overline{y} }_{r}, {\overline{X} }_{2},{\overline{x} }_{n} \right)~ and~~ {\varphi }_{3}\left({\overline{y} }_{r}, {\overline{Z} }_{3},{\overline{z} }_{{n^{'}}}\right)$ is not unique. Many estimators for $\overline{Y }$ can be suggested for different choices of ratio and regression type predictors which is displayed as in the Table 1. below.

Table 1 Different choices of ${T}_{i}$’s

In the following section, we shall discuss properties of the proposed classes of estimators. Up to first order of approximation, the expressions of bias and mean square errors are obtained.

5 Biases and Mean Square Errors of Proposed Classes of Estimators ${\widehat{\overline{Y}} }_{i}(i=\mathrm{1,2},\mathrm{3,4})$

For the derivation of the bias and mean square errors of the proposed classes of estimators ${\widehat{\overline{Y}} }_{i}\left(i=\mathrm{1,2},\mathrm{3,4}\right),$ we take the following:

${\overline{y} }_{n}= \overline{Y }(1+{e}_{1})$, ${\overline{x} }_{n}= \overline{X }(1+{e}_{2})$, ${\overline{z} }_{n}= \overline{Z }(1+{e}_{3})$,

${\overline{x} }_{{n}^{\mathrm{^{\prime}}}}= \overline{X }(1+{e}_{4})$, ${\overline{z} }_{{n}^{\mathrm{^{\prime}}}}= \overline{Z }(1+{e}_{5})$, ${s}_{yx}\left(r\right)={S}_{yx}\left(1+{e}_{6}\right)$,

${s}_{x}^{2}\left(r\right)={{S}_{x}}^{2}\left(1+{e}_{7}\right)$, ${\overline{y} }_{r}=$ $\overline{Y }\left(1+{e}_{8}\right),$ ${\overline{x} }_{r}=\overline{X }\left(1+{e}_{9}\right)$

Assuming large sample situation the expectations used are as under:

$$\left.\begin{array}{c}\begin{array}{c}E\left({e}_{i}\right)=0 ~~and~~ \left|{e}_{i}\right|=0~~ for~~ i=\mathrm{1,2},\dots .,9.\\ E\left({{e}_{1}}^{2}\right)={\lambda }_{1}{C}_{y}^{2}, E\left({{e}_{2}}^{2}\right)={\lambda }_{1}{C}_{x}^{2}, E\left({{e}_{3}}^{2}\right)={\lambda }_{1}{C}_{z}^{2}, E\left({{e}_{4}}^{2}\right)={\lambda }_{3}{C}_{x}^{2},\\ \\ E\left({{e}_{5}}^{2}\right)={\lambda }_{3}{C}_{z}^{2}, E\left({{e}_{8}}^{2}\right)={\lambda }_{2}{C}_{y}^{2}, E\left({{e}_{9}}^{2}\right)={\lambda }_{2}{C}_{x}^{2} ,\\ E\left({e}_{4}{e}_{8}\right)={\lambda }_{3}{\rho }_{yx}{C}_{y}{C}_{x}, E\left({e}_{2}{e}_{8}\right)={\lambda }_{1}{\rho }_{yx}{C}_{y}{C}_{x}, E\left({e}_{3}{e}_{4}\right)={\lambda }_{3}{\rho }_{xz}{C}_{x}{C}_{z}.\end{array}\\ E\left({e}_{5}{e}_{8}\right)={\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}\end{array}\right]$$

All the four proposed estimators ${\widehat{\overline{Y}} }_{i}(i=\mathrm{1,2},\mathrm{3,4})$ can be represented in terms of ${e}_{i} s$. So, on retaining terms up to second degree of ${e}_{i} s$ only, we have:

$${\widehat{\overline{Y}} }_{1} =\overline{Y }\left(1-{e}_{5}+{e}_{5}^{2}+{e}_{8}-{e}_{5}{e}_{8}\right)+\overline{X}{h }_{2}{p}_{2}\left({e}_{2}-{e}_{9}\right)+\overline{X}{h }_{2}^{'}{p}_{3}\left({e}_{4}-{e}_{2}\right)+\frac{1}{2!}\left[{h}_{22}{\overline{X} }^{2}\frac{{\left(n{e}_{2}-r{e}_{9}\right)}^{2}}{{\left(n-r\right)}^{2}}+{h}_{33}{\overline{X} }^{2}{e}_{9}^{2}+2{h}_{13}{{e}_{8}e}_{9}\bar{X}\bar{Y}+2{h}_{12}\left(\frac{{ne}_{2}{e}_{8}-r{e}_{9}{e}_{8}}{n-r}\right)\bar{X}\bar{Y}+2{h}_{23}\left(\frac{{ne}_{2}{e}_{9}-r{e}_{9}^{2}}{n-r}\right){\overline{X} }^{2}\right]+\frac{1}{2!}\left[{h}_{22}^{'}{\overline{X} }^{2}\frac{{\left({n^{'}}{e}_{4}-n{e}_{2}\right)}^{2}}{{\left({n^{'}}-n\right)}^{2}}+{h}_{33}^{'}{\overline{X} }^{2}{e}_{2}^{2}+2{h}_{13}^{'}{{e}_{2}e}_{8}\bar{X}\bar{Y}+2{h}_{12}^{'}\left(\frac{{{n^{'}}{e}_{4}e}_{8}-n{e}_{2}{e}_{8}}{{n^{'}}-n}\right)\bar{X}\bar{Y}+2{h}_{23}^{'}\left(\frac{{{n^{'}}e}_{4}{e}_{2}-n{e}_{2}^{2}}{{n^{'}}-n}\right){\overline{X} }^{2}\right]$$

(3)

$${\widehat{\overline{Y}} }_{2}= \overline{Y }\left(1+{e}_{8}\right)+\overline{X}{h }_{2}{p}_{2}\left({e}_{2}-{e}_{9}\right)+\overline{X}{h }_{2}^{'}{p}_{3}\left({e}_{4}-{e}_{2}\right)-{h}_{2}^{{\prime}{\prime}}{e}_{5}\overline{Z }+\frac{1}{2!}\left[{h}_{22}{\overline{X} }^{2}\frac{{\left(n{e}_{2}-r{e}_{9}\right)}^{2}}{{\left(n-r\right)}^{2}}+{h}_{33}{\overline{X} }^{2}{e}_{9}^{2}+2{h}_{13}{{e}_{8}e}_{9}\bar{X}\bar{Y}+2{h}_{12}\left(\frac{{ne}_{2}{e}_{8}-r{e}_{9}{e}_{8}}{n-r}\right)\bar{X}\bar{Y}+2{h}_{23}\left(\frac{{ne}_{2}{e}_{9}-r{e}_{9}^{2}}{n-r}\right){\overline{X} }^{2}\right]+\frac{1}{2!}\left[{h}_{22}^{'}{\overline{X} }^{2}\frac{{\left({n^{'}}{e}_{4}-n{e}_{2}\right)}^{2}}{{\left({n^{'}}-n\right)}^{2}}+{h}_{33}^{'}{\overline{X} }^{2}{e}_{2}^{2}+2{h}_{13}^{'}{{e}_{2}e}_{8}\bar{X}\bar{Y}+2{h}_{12}^{'}\left(\frac{{{n^{'}}{e}_{4}e}_{8}-n{e}_{2}{e}_{8}}{{n^{'}}-n}\right)\bar{X}\bar{Y}+2{h}_{23}^{'}\left(\frac{{{n^{'}}e}_{4}{e}_{2}-n{e}_{2}^{2}}{{n^{'}}-n}\right){\overline{X} }^{2}\right]+\frac{1}{2!}\left[{\frac{{n^{'}}^{2}}{{\left(N-{n^{'}}\right)}^{2}}h_{22}^{''}}{e}_{5}^{2}{\overline{Z} }^{2}+{h}_{33}^{{\prime}{\prime}}{e}_{5}^{2}{\overline{Z} }^{2}-2\left(\frac{{n^{'}}}{N-{n^{'}}}\right){h}_{12}^{{\prime}{\prime}}{e}_{5}{e}_{8}\overline{Y }\overline{Z }+2{h}_{13}^{{\prime}{\prime}}{e}_{5}{e}_{8}\bar{Y}\bar{Z}-2\left(\frac{{n^{'}}}{N-{n^{'}}}\right){h}_{23}^{{\prime}{\prime}}{e}_{5}^{2}{\overline{Z} }^{2}\right]$$

(4)

$${\widehat{\overline{Y}} }_{3}= \overline{Y }\left(1+{e}_{8}\right)\left[{k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right]+\overline{X}{h }_{12}{p}_{2}\left({e}_{2}-{e}_{9}\right)+\overline{X}{h }_{22}{p}_{3}\left({e}_{4}-{e}_{2}\right)-{k}_{2}\overline{Z}{e }_{5}+ \frac{1}{ 2!}\left[{h}_{22}{\overline{X} }^{2}\frac{{\left(n{e}_{2}-r{e}_{9}\right)}^{2}}{{\left(n-r\right)}^{2}}+{h}_{33}{\overline{X} }^{2}{e}_{9}^{2}+2{h}_{13}{{e}_{8}e}_{9}\bar{X}\bar{Y}+2{h}_{12}\left(\frac{{ne}_{2}{e}_{8}-r{e}_{9}{e}_{8}}{n-r}\right)\bar{X}\bar{Y}+2{h}_{23}\left(\frac{{ne}_{2}{e}_{9}-r{e}_{9}^{2}}{n-r}\right){\overline{X} }^{2}\right] \frac{1}{2!}\left[{h}_{22}^{'}{\overline{X} }^{2}\frac{{\left({n^{'}}{e}_{4}-n{e}_{2}\right)}^{2}}{{\left({n^{'}}-n\right)}^{2}}+{h}_{33}^{'}{\overline{X} }^{2}{e}_{2}^{2}+2{h}_{13}^{'}{{e}_{2}e}_{8}\bar{X}\bar{Y}+2{h}_{12}^{'}\left(\frac{{{n^{'}}{e}_{4}e}_{8}-n{e}_{2}{e}_{8}}{{n^{'}}-n}\right)\bar{X}\bar{Y}+ 2{h}_{23}^{'}\left(\frac{{{n^{'}}e}_{4}{e}_{2}-n{e}_{2}^{2}}{{n^{'}}-n}\right){\overline{X} }^{2}\right]$$

(5)

$${\widehat{\overline{Y}} }_{4}= \overline{Y }\left({p}_{3}\left(1+{e}_{8}\right)+{k}_{1}(\left(1-{p}_{3}\right)\left(1+{e}_{8}\right)-\frac{{e}_{5}}{2}-\frac{{e}_{5}{e}_{8}}{2}+\frac{(3-4{p}_{3}){{e}_{5}}^{2}}{8\left(1-{p}_{3}\right)}\right)+\overline{X }\left({h}_{12}{p}_{2}\left({e}_{2}-{e}_{9}\right)+{p}_{3}\left({e}_{4}-{e}_{2}\right)\right)+{k}_{2}\overline{Z }\left(-{e}_{5}+\frac{{{e}_{5}}^{2}}{2\left(1-{p}_{3}\right)}\right)+\frac{1}{2!}\left[{h}_{22}{\overline{X} }^{2}\frac{{\left(n{e}_{2}-r{e}_{9}\right)}^{2}}{{\left(n-r\right)}^{2}}+{h}_{33}{\overline{X} }^{2}{e}_{9}^{2}+2{h}_{13}{{e}_{8}e}_{9}\bar{X}\bar{Y}+2{h}_{12}\left(\frac{{ne}_{2}{e}_{8}-r{e}_{9}{e}_{8}}{n-r}\right)\bar{X}\bar{Y}+2{h}_{23}\left(\frac{{ne}_{2}{e}_{9}-r{e}_{9}^{2}}{n-r}\right){\overline{X} }^{2}\right]+\frac{1}{2!}\left[{h}_{22}^{'}{\overline{X} }^{2}\frac{{\left({n^{'}}{e}_{4}-n{e}_{2}\right)}^{2}}{{\left({n^{'}}-n\right)}^{2}}+{h}_{33}^{'}{\overline{X} }^{2}{e}_{2}^{2}+2{h}_{13}^{'}{{e}_{2}e}_{8}\bar{X}\bar{Y}+2{h}_{12}^{'}\left(\frac{{{n^{'}}{e}_{4}e}_{8}-n{e}_{2}{e}_{8}}{{n^{'}}-n}\right)\bar{X}\bar{Y}+2{h}_{23}^{'}\left(\frac{{{n^{'}}e}_{4}{e}_{2}-n{e}_{2}^{2}}{{n^{'}}-n}\right){\overline{X} }^{2}\right]$$

(6)

(i) For class of estimators $\varvec{{\widehat{\overline{Y}} }_{1}}$

On taking expectations on both sides of result (3), the bias of ${\widehat{\overline{Y}} }_{1}$, up to the terms of order $o\left({n}^{-1}\right)$ is:

$$B\left({\widehat{\overline{Y}} }_{1}\right)= {\lambda }_{3}\overline{Y }\left({C}_{z}^{2}-{\rho }_{yz}{C}_{y}{C}_{z}\right)+\left[\frac{{h}_{22}}{2\left(n-r\right)N}\left({n}^{2}{\lambda }_{1}+{r}^{2}{\lambda }_{2}-2nr{\lambda }_{1}\right)+\frac{{h}_{22}^{'}}{2\left({n^{'}}-n\right)N}\left({n^{'}}^{2}{\lambda }_{3}+{n}^{2}{\lambda }_{1}-2n{n^{'}}{\lambda }_{3}\right)+\frac{1}{2}{\lambda }_{2}{h}_{33}\left({p}_{2}-{p}_{1}\right)+\frac{1}{2}{\lambda }_{1}{h}_{33}^{'}\left({p}_{3}-{p}_{2}\right)+{h}_{23}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{23}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)\right]{\overline{X} }^{2}{C}_{x}^{2}+{[h}_{13}{\lambda }_{2}\left({p}_{2}-{p}_{1}\right)+{h}_{13}^{'}{\lambda }_{1}\left({p}_{3}-{p}_{2}\right)+{h}_{12}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{12}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)]{\rho }_{yx}\bar{Y}\bar{X}C_{y}{C}_{x}$$

The expression of $MSE\left({\widehat{\overline{Y}} }_{1}\right)$, up to first order of approximation, will be

$$MSE\left({\widehat{\overline{Y}} }_{1}\right)=E{\left({\widehat{\overline{Y}} }_{1}-\overline{Y }\right)}^{2}$$

$$={\overline{Y} }^{2}\left({\lambda }_{3}{C}_{z}^{2}+{\lambda }_{2}{C}_{y}^{2}-{\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}\right)+{\overline{X} }^{2}\left[{p}_{2}^{2}{h}_{2}^{2}\left({\lambda }_{2}-{\lambda }_{1}\right){C}_{x}^{2}+{ p}_{3}^{2}{h}_{2}^{{\prime}2}\left({\lambda }_{1}-{ \lambda }_{3}\right){C}_{x}^{2}\right]+2{\rho }_{yx}{C}_{y}{C}_{x}\bar{Y }\bar{X }\left({p}_{2}{h}_{2}\left({\lambda }_{1}-{\lambda }_{2}\right)+{p}_{3}{h}_{2}^{'}\left({\lambda }_{3}-{\lambda }_{1}\right)\right)$$

(7)

The optimum choices of ${h}_{2}$ and ${h}_{2}^{'}$ are obtained by minimizing the mean square error given in Eq. (7) with respect to ${h}_{2}$ and ${h}_{2}^{'}$. So, these are obtained as:

${h}_{2}(opt)=\frac{{\rho }_{yx}{S}_{y}}{{p}_{2}{S}_{x}}$ and ${h}_{2}^{'}(opt)=\frac{{\rho }_{yx}{S}_{y}}{{p}_{3}{S}_{x}}$.

Hence, for the class of estimators ${\widehat{\overline{Y}} }_{1}, \mathrm{the~ minimum~ mean~ square~ error}$ is

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{1}\right)={\overline{Y} }^{2}\left({\lambda }_{3}{C}_{z}^{2}+{\lambda }_{2}{C}_{y}^{2}-{2\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}\right)+ \left({\lambda }_{3}-{\lambda }_{2}\right){\rho }_{yx}^{2}{S}_{y}^{2}$$

(8)

(ii) For class of estimators $\varvec{{\widehat{\overline{Y}} }_{2}}$

Bias of ${\widehat{\overline{Y}} }_{2}$, is obtained by taking expectations on both sides of result (4), up to the terms of order $o\left({n}^{-1}\right)$ and is as follows:

$$B\left({\widehat{\overline{Y}} }_{2}\right)=\left[\frac{{h}_{22}}{2\left(n-r\right)N}\left({n}^{2}{\lambda }_{1}+{r}^{2}{\lambda }_{2}-2nr{\lambda }_{1}\right)+\frac{{h}_{22}^{'}}{2\left({n^{'}}-n\right)N}\left({n^{'}}^{2}{\lambda }_{3}+{n}^{2}{\lambda }_{1}-2n{n^{'}}{\lambda }_{3}\right)+\frac{1}{2}{\lambda }_{2}{h}_{33}\left({p}_{2}-{p}_{1}\right)+\frac{1}{2}{\lambda }_{1}{h}_{33}^{'}\left({p}_{3}-{p}_{2}\right)+{h}_{23}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{23}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)\right]{\overline{X} }^{2}{C}_{x}^{2}+{[h}_{13}{\lambda }_{2}\left({p}_{2}-{p}_{1}\right)+{h}_{13}^{'}{\lambda }_{1}\left({p}_{3}-{p}_{2}\right)+{h}_{12}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{12}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)]{\rho }_{yx}{\bar{Y }\bar{X}C }_{y}{C}_{x}+\frac{{h}_{22}^{{\prime}{\prime}}}{2\left(N-{n^{'}}\right)N}{n^{'}}^{2}{\lambda }_{3}{\overline{Z} }^{2}{C}_{z}^{2}+\left[\left(1-{p}_{3}\right){h}_{33}^{{\prime}{\prime}}{\lambda }_{3}-{\lambda }_{3}{h}_{23}^{{\prime}{\prime}}{p}_{3}\right]{\overline{Z} }^{2}{C}_{z}^{2}+\left[\left(1-{p}_{3}\right){h}_{13}^{{\prime}{\prime}}{\lambda }_{3}-{\lambda }_{3}{h}_{12}^{{\prime}{\prime}}{p}_{3}\right]{\rho }_{yz}{\bar{Y }\bar{Z}C }_{y}{C}_{z}$$

The expression of $MSE\left({\widehat{\overline{Y}} }_{2}\right)$, up to first order of approximation will be:

$$MSE\left({\widehat{\overline{Y}} }_{2}\right)=E{\left({\widehat{\overline{Y}} }_{2}-\overline{Y }\right)}^{2} ={\overline{Y} }^{2}{\lambda }_{2}{C}_{y}^{2}+{\overline{X} }^{2}\left[{p}_{2}^{2}{h}_{2}^{2}\left({\lambda }_{2}-{\lambda }_{1}\right){C}_{x}^{2}+{p}_{3}^{2}{h}_{2}^{{\prime}2}\left({\lambda }_{1}-{\lambda }_{3}\right){C}_{x}^{2}\right]+2{\rho }_{yx}{C}_{y}{C}_{x}\bar{Y }\bar{X }\left({p}_{2}{h}_{2}\left({\lambda }_{1}- {\lambda }_{2}\right)+{p}_{3}{h}_{2}^{'}\left({\lambda }_{3}-{\lambda }_{1}\right)\right)+{\lambda }_{3}{h}_{2}^{{\prime}{\prime}2}{C}_{z}^{2}{\overline{Z} }^{2}-2{h}_{2}^{{\prime}{\prime}}{\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}\bar{Y }\bar{Z }$$

(9)

The optimum choices of${h}_{2}$, ${h}_{2}^{'}$ $,$ and ${h}_{2}^{{\prime}{\prime}}$ are obtained by minimizing the mean square error given in Eq. (9) with respect to ${h}_{2}$, ${h}_{2}^{'}$ $,$ and ${h}_{2}^{{\prime}{\prime}}$ and these are given as.

${h}_{2}(opt)=\frac{{\rho }_{yx}{S}_{y}}{{p}_{2}{S}_{x}}$, ${h}_{2}^{\mathrm{^{\prime}}}(opt)=\frac{{\rho }_{yx}{S}_{y}}{{p}_{3}{S}_{x}}$ , ${h}_{2}^{\mathrm{^{\prime}}\mathrm{^{\prime}}}(opt)=\frac{{\rho }_{yz}{S}_{y}}{{S}_{z}}$

For the class of estimators ${\widehat{\overline{Y}} }_{2},$ the minimum mean square error is obtained as

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)={\overline{Y} }^{2}{\lambda }_{2}{\left(1-{\rho }_{yx}^{2}\right)C}_{y}^{2}+ {\lambda }_{3}\left({\rho }_{yx}^{2}-{\rho }_{yz}^{2}\right){S}_{y}^{2}$$

(10)

(iii) For class of estimators $\varvec{{\widehat{\overline{Y}} }_{3}}$

On taking expectations on both sides of result (5), the bias of estimator ${\widehat{\overline{Y}} }_{3}$, up to the terms of order $o\left({n}^{-1}\right)$ is:

$$B\left({\widehat{\overline{Y}} }_{3}\right)= \overline{Y }\left(\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right)-1\right)+\left[\frac{{h}_{22}}{2\left(n-r\right)N}\left({n}^{2}{\lambda }_{1}+{r}^{2}{\lambda }_{2}-2nr{\lambda }_{1}\right)+\frac{{h}_{22}^{'}}{2\left({n^{'}}-n\right)N}\left({n^{'}}^{2}{\lambda }_{3}+{n}^{2}{\lambda }_{1}-2n{n^{'}}{\lambda }_{3}\right)+\frac{1}{2}{\lambda }_{2}{h}_{33}\left({p}_{2}-{p}_{1}\right)+\frac{1}{2}{\lambda }_{1}{h}_{33}^{'}\left({p}_{3}-{p}_{2}\right)+{h}_{23}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{23}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)\right]{\overline{X} }^{2}{C}_{x}^{2}+{[h}_{13}{\lambda }_{2}\left({p}_{2}-{p}_{1}\right)+{h}_{13}^{'}{\lambda }_{1}\left({p}_{3}-{p}_{2}\right)+{h}_{12}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{12}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)]{\rho }_{yx}{\bar{Y }\bar{X}C }_{y}{C}_{x}$$

The expression of $MSE\left({\widehat{\overline{Y}} }_{3}\right)$, up to first order of approximation will be.

M $SE\left({\widehat{\overline{Y}} }_{3}\right)=E{\left({\widehat{\overline{Y}} }_{3}-\overline{Y }\right)}^{2}$

$$= {\overline{Y} }^{2}\left({\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right)}^{2}\left(1+{\lambda }_{2}{C}_{y}^{2}\right)+1-2\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right)\right)+{\overline{X} }^{2}\left[{p}_{2}^{2}{h}_{2}^{2}\left({\lambda }_{2}-{ \lambda }_{1}\right){C}_{x}^{2}+{p}_{3}^{2}{h}_{2}^{{\prime}2}\left({\lambda }_{1}-{\lambda }_{3}\right){C}_{x}^{2}\right]+2\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){\rho }_{yx}{C}_{y}{C}_{x}\bar{Y }\bar{X }\left({p}_{2}{h}_{2}\left({\lambda }_{1}-{\lambda }_{2}\right)+ {p}_{3}{h}_{2}^{'}\left({\lambda }_{3}-{\lambda }_{1}\right)\right)+{\lambda }_{3}{k}_{2}^{2}{C}_{z}^{2}{\overline{Z} }^{2}-2\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){k}_{2}{\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}\bar{Y }\bar{Z }$$

(11)

The optimum choices of ${h}_{2}$, ${h}_{2}^{'}, {k}_{1}$ and ${k}_{2}$ are obtained by minimizing the mean square error given in Eq. (11) with respect to as ${h}_{2}$, ${h}_{2}^{'}, {k}_{1}$ and ${k}_{2}$ and these are given as.

${h}_{2}(opt)=\frac{\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){\rho }_{yx}{S}_{y}}{{p}_{2}{S}_{x}}$, ${h}_{2}^{\mathrm{^{\prime}}}(opt)=\frac{\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){\rho }_{yx}{S}_{y}}{{p}_{3}{S}_{x}}$ ,${k}_{2}(opt)=\frac{{\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right)\rho }_{yz}{S}_{y}}{{S}_{z}}$,

$${k}_{1}(opt)=\left(\left(\frac{1}{1+{\lambda }_{2}{\left(1-{\rho }_{yx}^{2}\right)C}_{y}^{2}+ {\lambda }_{3}\left({\rho }_{yx}^{2}-{\rho }_{yz}^{2}\right){C}_{y}^{2}}\right)-{p}_{3}\right)/\left(1-{p}_{3}\right)$$

The minimum mean square error of the class of estimators ${\widehat{\overline{Y}} }_{3}$ is obtained as:

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)=\frac{{\overline{Y} }^{2}{(\lambda }_{2}{\left(1-{\rho }_{yx}^{2}\right)S}_{y}^{2}+ {\lambda }_{3}\left({\rho }_{yx}^{2}-{\rho }_{yz}^{2}\right){S}_{y}^{2})}{{\overline{Y} }^{2}+{\overline{Y} }^{2}{\lambda }_{2}{\left(1-{\rho }_{yx}^{2}\right)C}_{y}^{2}+ {\lambda }_{3}\left({\rho }_{yx}^{2}-{\rho }_{yz}^{2}\right){S}_{y}^{2}}= \frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{1+\frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{{\overline{Y} }^{2}}}$$

(12)

(iv) For class of estimators $\varvec{{\widehat{\overline{Y}} }_{4}}$

On taking expectations on both sides of result (6), the bias of estimator ${\widehat{\overline{Y}} }_{4}$, up to the terms of order $o\left({n}^{-1}\right)$ is:

$$B\left({\widehat{\overline{Y}} }_{4}\right)= \overline{Y }\left({p}_{3}+{k}_{1}\left(\left(1-{p}_{3}\right)-\frac{1}{2}{\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}+\frac{(3-4{p}_{3})}{8\left(1-{p}_{3}\right)}{\lambda }_{3}{C}_{z}^{2}\right)-1\right)+\frac{{k}_{2}}{2(1-{p}_{3})}{\lambda }_{3}\overline{Z}{C }_{z}^{2}+\left[\frac{{h}_{22}}{2\left(n-r\right)N}\left({n}^{2}{\lambda }_{1}+{r}^{2}{\lambda }_{2}-2nr{\lambda }_{1}\right)+\frac{{h}_{22}^{'}}{2\left({n^{'}}-n\right)N}\left({n^{'}}^{2}{\lambda }_{3}+{n}^{2}{\lambda }_{1}-2n{n^{'}}{\lambda }_{3}\right)+\frac{1}{2}{\lambda }_{2}{h}_{33}\left({p}_{2}-{p}_{1}\right)+\frac{1}{2}{\lambda }_{1}{h}_{33}^{'}\left({p}_{3}-{p}_{2}\right)+{h}_{23}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{23}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)\right]{\overline{X} }^{2}{C}_{x}^{2}+{[h}_{13}{\lambda }_{2}\left({p}_{2}-{p}_{1}\right)+{h}_{13}^{'}{\lambda }_{1}\left({p}_{3}-{p}_{2}\right)+{h}_{12}\left({p}_{2}{\lambda }_{1}-{p}_{1}{\lambda }_{2}\right)+{h}_{12}^{'}\left({p}_{3}{\lambda }_{3}-{p}_{2}{\lambda }_{1}\right)]{\rho }_{yx}{\bar{Y }\bar{X}C }_{y}{C}_{x}$$

The expression of $MSE\left({\widehat{\overline{Y}} }_{4}\right)$, up to first order of approximation will be

$$MSE\left({\widehat{\overline{Y}} }_{4}\right)=E{\left({\widehat{\overline{Y}} }_{4}-\overline{Y }\right)}^{2}$$

(13)

The optimum choices of ${h}_{2}, {h}_{2}^{'}$ $, {k}_{1}$ and ${k}_{2}$ are obtained by minimizing the mean square error obtained from Eq. (13) with respect to as ${h}_{2}$, ${h}_{2}^{'}, {k}_{1}$ and ${k}_{2}$ and are given as.

${h}_{2}(opt)=\frac{\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){\rho }_{yx}{S}_{y}}{{p}_{2}{S}_{x}}$, ${h}_{2}^{\mathrm{^{\prime}}}(opt)=\frac{\left({k}_{1}\left(1-{p}_{3}\right)+{p}_{3}\right){\rho }_{yx}{S}_{y}}{{p}_{3}{S}_{x}}$ ,

${k}_{2}(opt)=-\frac{\overline{Y} }{{\overline{Z}C }_{z}}\left[{k}_{1}\left({C}_{z}-\left(1-{p}_{3}\right){\rho }_{yz}{C}_{y}\right)+\left(-{p}_{3}{\rho }_{yz}{C}_{y}-\frac{{C}_{z}}{2}\right)\right]$,

$${k}_{1}(opt)=\frac{{\left(1-{p}_{3}\right)}^{2}{\overline{Y} }^{2}-{p}_{3}\left(1-{p}_{3}\right){MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)-\frac{1}{2}{p}_{3}{\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}{\overline{Y} }^{2}-\frac{1}{8}\left(1+4{p}_{3}\right){\lambda }_{3}{C}_{z}^{2}{\overline{Y} }^{2}}{{\overline{Y} }^{2}{\left(1-{p}_{3}\right)}^{2}+{\left(1-{p}_{3}\right)}^{2}{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}$$

The minimum mean square error of the class of estimators ${\widehat{\overline{Y}} }_{3}$ is obtained as

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right)= {MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)-\frac{\frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}}{{\overline{Y} }^{2}}}{1+\frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{{\overline{Y} }^{2}}}-\frac{\left(A.{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)+B \right)\frac{1}{{\left(1-{p}_{3}\right)}^{2}{\overline{Y} }^{2}}}{1+\frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{{\overline{Y} }^{2}}}$$

(14)

or

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right)= {MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)-\frac{\left(A.{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)+B \right)\frac{1}{{\left(1-{p}_{3}\right)}^{2}{\overline{Y} }^{2}}}{1+\frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{{\overline{Y} }^{2}}}$$

(15)

where $A={p}_{3}^{2}\left(1-{p}_{3}\right){\lambda }_{3}{\rho }_{yz}{C}_{y}{C}_{z}{\overline{Y} }^{2}+{\lambda }_{3}{C}_{z}^{2}{\overline{Y} }^{2}\left({p}_{3}^{3}+\frac{{\left(1-{p}_{3}\right)}^{2}}{4}+\left(1+4{p}_{3}\right){p}_{3}\left(1-{p}_{3}\right)\right)$

$$B= {\lambda }_{3}^{2}\left[\frac{1}{64}{\left(4{p}_{3}-1\right)}^{2}{C}_{z}^{4}{\overline{Y} }^{4}+\frac{1}{4}{p}_{3}{\rho }_{yz}{C}_{y}{C}_{z}^{3}{\overline{Y} }^{4}+{p}_{3}^{2}{\rho }_{yz}^{2}{C}_{y}^{2}{C}_{z}^{2}{\overline{Y} }^{4}\right].$$

6 Relative Performances of Proposed Classes of Estimators

Here, we shall compare the $MSE$ of the proposed classes of estimators with the regression type estimator in one phase sampling and two phase sampling. So, the following results are derived.

$MSE\left({\overline{y} }_{reg1}\right)-MSE\left({\overline{y} }_{reg2}\right)=\left(\frac{1}{{n^{'}}}-\frac{1}{N}\right){S}_{y}^{2}+\left(\frac{1}{n}-\frac{1}{N}\right){\rho }_{yx}^{2}{S}_{y}^{2}>0,$ always.

$MSE\left({\overline{y} }_{reg1}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{1}\right)>0,$ if ${\rho }_{yz}>\frac{1}{2}\frac{{C}_{z}}{{C}_{y}}$.

$MSE\left({\overline{y} }_{reg1}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)= {S}_{y}^{2}\left[\left(\frac{1}{n}-\frac{1}{{n^{'}}}\right){\rho }_{yx}^{2}+{\lambda }_{3}{\rho }_{yz}^{2}\right] >0,$ always.

$MSE\left({\overline{y} }_{reg1}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right) = {S}_{y}^{2}\left[\left(\frac{1}{n}-\frac{1}{{n^{'}}}\right){\rho }_{yx}^{2}+{\lambda }_{3}{\rho }_{yz}^{2}\right]+\frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}}{{{\overline{Y} }^{2}+MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)} >0,$ always.

$MSE\left({\overline{y} }_{reg1}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right)={S}_{y}^{2}\left[\left(\frac{1}{n}-\frac{1}{{n^{'}}}\right){\rho }_{yx}^{2}+{\lambda }_{3}{\rho }_{yz}^{2}\right]+\frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}+\left(A.{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)+B \right)\frac{1}{{\left(1-{p}_{3}\right)}^{2}}}{{{\overline{Y} }^{2}+MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}> 0,$ always.

$MSE\left({\overline{y} }_{reg2}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{1}\right)>0$ if ${\rho }_{yz}>\frac{1}{2}\frac{{C}_{z}}{{C}_{y}}$.

$MSE\left({\overline{y} }_{reg2}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)={\lambda }_{3}{\rho }_{yz}^{2}{S}_{y}^{2}>0,$ always.

$MSE\left({\overline{y} }_{reg2}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)={\lambda }_{3}{\rho }_{yz}^{2}{S}_{y}^{2}+\frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}}{{{\overline{Y} }^{2}+MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)} >0,$ always.

$MSE\left({\overline{y} }_{reg2}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right)={\lambda }_{3}{\rho }_{yz}^{2}{S}_{y}^{2}+ \frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}+\left(A.{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)+B \right)\frac{1}{{\left(1-{p}_{3}\right)}^{2}}}{{{\overline{Y} }^{2}+MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}>0,$ always.

${MSE}_{min}\left({\widehat{\overline{Y}} }_{1}\right)- {MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right) ={\lambda }_{3}{\overline{Y} }^{2}{\left({C}_{z}-{\rho }_{yz}{C}_{y}\right)}^{2}>0,$ always.

${MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)- {MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)= \frac{{\left({MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)\right)}^{2}}{{{\overline{Y} }^{2}+MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}>0$ always.

${MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)-{MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right)=\frac{\left(A.{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)+B \right)\frac{1}{{\left(1-{p}_{3}\right)}^{2}{\overline{Y} }^{2}}}{1+\frac{{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)}{{\overline{Y} }^{2}}}>0,$ always.

In addition to the above results, we also noticed the following result:

$${MSE}_{min}\left({\widehat{\overline{Y}} }_{1}\right)>{MSE}_{min}\left({\widehat{\overline{Y}} }_{2}\right)>{MSE}_{min}\left({\widehat{\overline{Y}} }_{3}\right)>{MSE}_{min}\left({\widehat{\overline{Y}} }_{4}\right).$$

From these results, it is clear that all the four classes are superior to regression type of estimators, both in single phase and double phase sampling, except in case of class ${\widehat{\overline{Y}} }_{1}$, which is superior under the optimal condition.

7 Numerical Illustrations

To support the theoretical results obtained in the previous section, we have considered five empirical data sets and three hypothetical data sets.

7.1 Empirical Study

The effectiveness of our suggested classes of estimators has been demonstrated using the following five empirical data sets. According to their respective percent relative efficiencies, the performance of the suggested imputation approaches is compared. So, we have calculated the percent relative efficiencies (PREs) of the estimators with respect to the estimator ${\overline{y} }_{reg1}$ for different response rates by using the following expression:

$$PRE\left({\overline{y} }_{o} \right)= \frac{MSE({\overline{y} }_{reg1})}{ {MSE}_{min}\left({\overline{y} }_{o}\right)} \times 100$$

where ${\overline{y} }_{o}$ = ${\overline{y} }_{reg2}, {\widehat{\overline{Y}} }_{1}, {\widehat{\overline{Y}} }_{2},{\widehat{\overline{Y}} }_{3},{\widehat{\overline{Y}} }_{4}$.

The description of values of population parameters in case of empirical data sets along with the source of population are given as follows:

Population 1- Source: Cochran [43]

Y: Number of ‘placebo’ children.

X: Number of paralytic polio cases in the placebo group.

Z: Number of paralytic polio cases in the ‘not inoculated’ group.

N = 34, ${n^{'}}=15,$ n = 10, $\overline{Y }=4.92$, $\overline{X }=2.59$, $\overline{Z }=2.91$, ${C}_{y}^{2}=1.0248$, ${C}_{x}^{2}=1.5175$, ${C}_{z}^{2}=1.1492$, ${\rho }_{yx}=0.7326$, ${\rho }_{xz}=0.6837$, ${\rho }_{yz}=0.6430.$

Population 2- Source: Murthy [44]

Y: Area under wheat in 1964.

X: Area under wheat in 1963.

Z: Area under wheat in 1961.

N = 34, ${n^{'}}=25,$ n = 20, $\overline{Y }=199.44 acre$, $\overline{X }=208.89 acre$, $\overline{Z }=747.59 acre$, ${C}_{y}^{2}=0.5673$, ${C}_{x}^{2}=0.5191$, ${C}_{z}^{2}=0.3527$, ${\rho }_{yx}=0.9801$, ${\rho }_{xz}=0.9097$, ${\rho }_{yz}=0.9043.$

Population 3- Source: Sukhatme and Chand [45]

Y: Apple trees of bearing age in 1964.

X: Bushels of apples harvested in 1964.

Z: Bushels of apples harvested in 1959.

N = 200, ${n^{'}}=30,$ n = 20, $\overline{Y }=1031.82$, $\overline{X }=2934.58$, $\overline{Z }=3651.49$, ${C}_{y}^{2}=2.55280$, ${C}_{x}^{2}=4.02504$, ${C}_{z}^{2}=2.09379$, ${\rho }_{yx}=0.93$, ${\rho }_{xz}=0.84$, ${\rho }_{yz}=0.77.$

Population 4- Source: Shukla and Thakur [6]

Y: Artificially generated study variable.

X: Artificially generated first auxiliary variable.

Z: Artificially generated second auxiliary variable.

N = 200, ${n^{'}}=80,$ n = 30, $\overline{Y }=42.485$, $\overline{X }=18.515$, $\overline{Z }=20.52$, ${C}_{y}^{2}=0.1080$, ${C}_{x}^{2}=0.1410$, ${C}_{z}^{2}=0.1086$, ${\rho }_{yx}=0.8734$, ${\rho }_{xz}=0.9943$, ${\rho }_{yz}=0.8667.$

Population 5- Source: Handiquer et al. [46]

Y: Forest timber volume in cubic meter (Cum) in 0.1 ha sample plot.

X: Average tree height in the sample plot in meter (m).

Z: Average crown diameter in the sample plot in meter (m).

N = 2500, ${n^{'}}=200,$ n = 80, $\overline{Y }=4.63$, $\overline{X }=21.09$, $\overline{Z }=13.55$, ${C}_{y}^{2}=0.9025$, ${C}_{x}^{2}=0.9604$, ${C}_{z}^{2}=0.4096$, ${\rho }_{yx}=0.79$, ${\rho }_{xz}=0.66$, ${\rho }_{yz}=072.$

7.2 Simulation Study

In this section, using R software, a simulation study has been conducted to examine the percent relative efficiency of suggested estimators owing to the existence of non-response in the population.

The simulation study is carried in the following stages:

Stage I: Obtain first phase sample ${S^{'}}$ of size ${n^{'}}$ from population of size N using SRSWOR scheme.

Stage II: From first phase sample, draw second phase sample S of size n using again SRSWOR scheme.

Stage III: Remove $\left(n-r\right)$ sample units from sample S randomly.

Stage IV: The dropped units are then imputed using proposed imputation techniques considered for the sample.

Stage V: Obtain the value of estimator $\widehat{\overline{Y} }$ of $\overline{Y }.$

Stage VI: The above steps are repeated 50,000 times so that we have got 50,000 values of $\widehat{\overline{Y} }$ i.e.${\widehat{\overline{Y}} }_{i}$; i $=\mathrm{1,2},3, . . . ,50000.$

$MSE\left({\widehat{\overline{Y}} }_{i}\right)=\frac{1}{50000} \sum_{i=1}^{50000}{({\widehat{\overline{Y}} }_{i}-\overline{Y })}^{2}$.

The following is a description of artificial data sets:

Population 6- Source: [Artificial Population].

A population of size N = 1500 with Y as study variable, X, and Z as first and second auxiliary variables is created, with the following theoretical mean vector $\mu =[\mathrm{25,30,40}]$ and theoretical covariance matrix $\Sigma = \left[\begin{array}{ccc}15& 12& 10\\ 12& 11& 8\\ 10& 8& 10\end{array}\right]$ respectively from a multivariate normal distribution. We have taken ${n}{\prime}=$ 1200 and n $=900.$

Population 7- Source: [Artificial Population].

The study variable Y and two auxiliary variables X and Z are used to create an artificial population of size N = 650. While it has a weak correlation with Z, Y has a strong correlation with X. These variables were produced using a multivariate normal distribution, with the theoretical mean vector $\mu =[\mathrm{50,30,70}]$ and theoretical covariance matrix $\Sigma = \left[\begin{array}{ccc}1.4& 1.2& 1.0\\ 1.2& 1.5& 0.8\\ 1.0& 0.8& 1.2\end{array}\right]$ respectively. We have taken ${n^{'}}=$ 500 and n $=350.$

Population 8- Source: [Artificial Population].

An artificial population is generated of size N = 2000 which involves Y, X and Z as study variable, first and second auxiliary variables respectively. The study variable Y is highly correlated with X while it is correlated with Z due to its correlation with X. These variables are generated from a multivariate normal distribution with the following theoretical mean vector mean vector $\mu =[\mathrm{250,130,400}]$ and theoretical covariance matrix $\Sigma = \left[\begin{array}{ccc}1.5& 1.2& 1.0\\ 1.2& 1.2& 0.8\\ 1.0& 0.8& 2\end{array}\right]$ respectively. We have taken ${n^{'}}=$ 1500 and n $=1100.$

To have precise idea of the performance of proposed classes of estimators ${\widehat{\overline{Y}} }_{i}(i=\mathrm{1,2},\mathrm{3,4})$, in the section below, we show a graphic depiction of the estimators' PREs in relation to various response values.

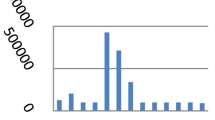
In order to improve the readability of the results and better comparison for different values of r, we have shown our findings using PREs of the regression type estimator in two-phase sampling and suggested classes of estimators for various values of r by using pictorial representation. Just for the rough idea, we have presented graphical representation only for Population 1, as the similar trend will be followed by all the proposed estimators in the remaining considered Populations 2—8. These results are shown in Fig. 1. The behavior of different considered estimators has been given with different specific colors which are further associated with different numbers like 1,2,3,4,5 corresponding to estimators ${\overline{y} }_{reg2}$, ${\widehat{\overline{Y}} }_{1}, {\widehat{\overline{Y}} }_{2}, {\widehat{\overline{Y}} }_{3}, {\widehat{\overline{Y}} }_{4}$ estimators respectively.

Fig. 1

Behavior of PRE of different proposed estimators with respect to different value of r

7.3 Results

The following results can be interpreted from Tables 2, 3, 4, 5, 6, 7, 8, and 9.

Table 2 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 1

Table 3 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 2

Table 4 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 3

Table 5 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 4

Table 6 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 5

Table 7 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 6

Table 8 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 7

Table 9 Percent Relative Efficiencies of different estimators with respect to ${\overline{y} }_{reg1}$ based on Population 8

(i) It is observed that percent relative efficiencies of all the proposed classes of estimators ${\widehat{\overline{Y}} }_{i}(i=\mathrm{1,2},\mathrm{3,4})$, perform better than conventional regression-type estimators defined in both in single phase and two-phase sampling schemes. Also, there is considerable gain in efficiency over the conventional regression-type estimators in all the proposed class of estimators.

(ii) For high response rate i.e. for greater increase in response rate in the sample, all the proposed classes of estimators gives sufficiently large gains in efficiencies over regression type estimator in single phase sampling.

(iii) It is observed that as the response rate rises, the percent relative efficiencies of all the proposed classes also increases, which indicates that all these proposed classes will perform more efficiently if number of responding units are sufficiently large.

(iv) It has been also observed that the PRE of proposed class of estimator ${\widehat{\overline{Y}} }_{4}$ is maximum, which reveals that this class of estimator is superior among all the proposed classes of estimators $\stackrel{-}{Y.}$

8 Conclusions

In the present study, four efficient classes of estimators have been proposed for efficient estimation of population mean, under two-phase sampling using two auxiliary variables. It has been seen that with the increase in response rate, the PREs of proposed classes increases, which indicates that our proposed classes of estimators could perform significantly better, if high number of responding units are available. A large number of estimators can be formed using different predictors belonging to different proposed classes, giving a large variety of strategies. The proposed classes of estimators can be utilized in real life scenario for efficient estimation of population mean.