An AI-driven Predictive Model for Pancreatic Cancer Patients Using Extreme Gradient Boosting

Abstract

Pancreatic cancer is one of the deadliest carcinogenic diseases affecting people all over the world. The majority of patients are usually detected at Stage III or Stage IV, and the chances of survival are very low once detected at the late stages. This study focuses on building an efficient data-driven analytical predictive model based on the associated risk factors and identifying the most contributing factors influencing the survival times of patients diagnosed with pancreatic cancer using the XGBoost (eXtreme Gradient Boosting) algorithm. The grid-search mechanism was implemented to compute the optimum values of the hyper-parameters of the analytical model by minimizing the root mean square error (RMSE). The optimum hyperparameters of the final analytical model were selected by comparing the values with 243 competing models. To check the validity of the model, we compared the model’s performance with ten deep neural network models, grown sequentially with different activation functions and optimizers. We also constructed an ensemble model using Gradient Boosting Machine (GBM). The proposed XGBoost model outperformed all competing models we considered with regard to root mean square error (RMSE). After developing the model, the individual risk factors were ranked according to their individual contribution to the response predictions, which is extremely important for pancreatic research organizations to spend their resources on the risk factors causing/influencing the particular type of cancer. The three most influencing risk factors affecting the survival of pancreatic cancer patients were found to be the age of the patient, current BMI, and cigarette smoking years with contributing percentages of 35.5%, 24.3%, and 14.93%, respectively. The predictive model is approximately 96.42% accurate in predicting the survival times of the patients diagnosed with pancreatic cancer and performs excellently on test data. The analytical methodology of developing the model can be utilized for prediction purposes. It can be utilized to predict the time to death related to a specific type of cancer, given a set of numeric, and non-numeric features.

1 Introduction

Pancreatic cancer continues to be one of the significant health hazards, and highly devastating gastrointestinal cancer affecting people all over the globe [25]. “Pancreatic cancer incidence rates are nearly similar to mortality rates due to high fatality rates” [35]. “According to the current health science researchers, this disease causes approximately 30,000 deaths per year in the USA” [31]. It is the fourth principal reason for cancer death in the USA and leads to an estimated 227,000 deaths per year worldwide. The incidence and number of fatalities from pancreatic tumors have been continuously increasing, while the incidence and mortality from other prevalent cancers have been decreasing. Despite advancements in pancreatic cancer detection and care, it is estimated that approximately 4% of patients will survive five years following diagnosis. [47]. After the detection of pancreatic cancer, doctors usually perform some additional tests to understand better if the cancer has been spread or the spreading area of cancer. Different imaging tests, such as a PET (Positron Emission Tomography) scan, have proven helpful to doctors in order to identify the presence of cancerous growths. With these tests, doctors try to establish the cancer’s stage. Staging helps explicate how advanced the cancer is. It also assists doctors in deciding the treatment options and alternatives. The following is the description of the stages used in our data set according to the definition of the Surveillance, Epidemiology, and End Results (SEER) database.¹

• Localized: No evidence that the malignancy has spread beyond the pancreas.

• Regional: Cancer has spread to neighboring structures or lymph nodes from the pancreas.

• Distant: Cancer has spread to other regions of the body, including the lungs, liver, and bones.

Risk factors for developing pancreatic cancer usually include family history, obesity, type 2 diabetes, and use of tobacco products. Even for the tiny proportion of patients who have a localized, resectable tumor, the prognosis remains poor, with only 20% surviving 5 years after surgery [37]. The outcome variable of our study is the survival time (in years). Although in most cases, pancreatic cancer remains incurable, researchers have concentrated on how to enhance the survival rates of individuals with pancreatic cancer. In our study, we developed a non-linear predictive model using Extreme Gradient Boosting (XGBoost) to estimate the survival time of patients diagnosed with pancreatic cancer. Given a set of risk factors (described in Section 2.1), our model predicts the survival of patients with a high degree of accuracy. We also compared our proposed model’s accuracy (in terms of RMSE) with Gradient Boosting Machines (GBM) and different deep-learning models. In recent years, researchers are prone to using sophisticated data-driven machine-learning models, decision-making models, and deep-learning algorithms in applied research because of their high predictive power and learning abilities from data [9, 10, 16, 17, 27, 36, 44, 48]. There is an increased tendency in the studies published in recent years that applied semi-supervised ML techniques for modeling cancer survival which address both labeled and unlabeled data. [39]. Kourou, Exarchos, et al., 2015 [28] presented a detailed review of the most recent ML research methods applicable to cancer prediction/prognosis with case studies. Ahmad, Eshlaghy, et al., [2] used different ML and DL algorithms like Decision Tree (DT), Support Vector Machine (SVM), and Artificial Neural Network (ANN) and compared their performance to predict the recurrence of breast cancer using 10-fold cross-validation. Hayward, Alvarez, et al., [23] developed different predictive models for the clinical performance of pancreatic cancer patients based on machine learning methods. The predictive performance of machine learning (ML) is compared with linear and logistic regression techniques. According to their study, ML offers techniques for improved prediction of clinical performance, and thus, these techniques can be considered as valuable alternatives to the conventional multivariate regression methods in clinical research. Wang & Yoon [32] suggested an online gradient boosting (GAOGB) model based on a genetic algorithm for incremental breast cancer (BC) prognosis. Their proposed GAOGB model was evaluated on the SEER database in terms of accuracy, the area under the curve (AUC), sensitivity, specificity, retraining time, and variation at each iteration. Ma, Meng, et al., [33] suggested a classification model that uses the power of extreme gradient boosting (XGBoost) in complicated multi-omics data to focus on early-stage and late-stage malignancies separately. Their XGBoost model was applied to four types of cancer data downloaded from The Cancer Genome Atlas (CGA), and the model’s performance was compared with other popular machine learning methods (ML) methods. The authors investigated the efficacy of XGBoost on the diagnostic categorization of malignancies in their study and found XGBoost as a robust predictive algorithm. Chen, Jia, et al., [15] proposed a non-parametric model for survival analysis that utilizes an ensemble of regression trees to determine the variation of hazard functions with respect to the associated risk factors. The scientists used GBMCI (gradient boosting machine for concordance index) software to develop their model and tested its effectiveness against other conventional survival models using a large-scale breast cancer prognostic dataset. In their study, they found the GBMCI to be consistently outperforming other methods based on a number of covariate settings. Amjad, Maaz, et al. used the XGBoost algorithm to predict the pile-bearing capacity values and obtained the highest performance capability when compared with the other competing models like AdaBoost, Random Forest, decision tree, and Support Vector Machine [3]. In a study conducted in Beijing, the researchers proposed a hypertensive outcome prediction model combining the gain sequence forward tabu search feature selection (GSFTS-FS) and XGBoost by utilizing the data from patients with hypertension and obtained an accuracy of 94.6% with AUC 0f 0.956 [11]. Shi, Xiupeng, et al. used XGBoost for driving assessment and risk prediction and Key feature selection were done by gain-based importance ranking and recursive elimination [42]. Yang, Jian, et al. proposed a SMOTE-based Xgboost methodology for heart disease prediction and obtained 93.44% prediction accuracy. The relative importance of the features was accessed using the information gain [50]. Li, Hua, et al. applied the XGBoost algorithm to the personal credit evaluation problem based on big data and obtained the highest model performance based on four model evaluation matrices (Accuracy, Kappa, AUC, and KS) when compared with four popular machine learning models (logistic regression, decision tree, random forest, and Gradient Boosting Decision Tree). [30]

2 Materials and Methods

2.1 Data Description

The study data has been obtained from National Cancer Institute (NIH). The data contains information on patients diagnosed with pancreatic adenocarcinoma. We treated the survival time (in days) as the response in developing our model and considered cause-specific death (deaths due to pancreatic cancer) for each patient. Patient survival time is one of the most crucial factors in all cancer studies. It is critical to assess the severity of cancer since it helps to determine the prognosis and find the best treatment options. There were a total of 800 patients’ information in our study after eliminating the missing observations for which several risk factors were missing. In our study, the response variable is the survival time of patients (in days). There are a total of ten risk factors used in our predictive analysis. Seven of those are categorical in nature, and three of them are numeric variables. The descriptions of the risk factors are as follows.

• 1. panc_exitage (Numeric) $(X_1)$: Age of diagnosis of the patient.

• 2. Stage (Categorical) $(X_2)$: Pancreatic Cancer Stages, categorized as a) localized, b) regional, and c) distant

• 3. asp (Categorical) $(X_3)$: Does the person use Aspirin Regularly?

• 4. ibup (Categorical) $(X_4)$: Does the person use Ibuprofen Regularly?

• 5. fh_Cancer (Categorical) $(X_5)$: The number of first-degree relatives with any type of cancer.

• 6. Sex (Categorical) $(X_6)$: Sex of the individual.

• 7. BMI (numeric) $(X_7)$: Current Body Mass Index (BMI) at Baseline (In lb/in2)

• 8. Cigarette Years (numeric) $(X_8)$: The total number of years the patient smoked.

• 9. gallblad_f (Categorical) $(X_9)$: Did the individual ever have gallbladder stones or inflammation?

• 10. hyperten_f (Categorical) $(X_{10})$: Did the individual ever have high blood pressure?

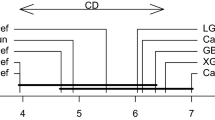
A schematic diagram of the data used in our study with the description of risk factors is shown in Fig. 1 below.

Fig. 1

Pancreatic Cancer Data with Relevant Risk Factors

As the above Fig. 1 illustrates, seven out of ten risk factors are categorical, having two or more categories. Before starting our analysis of the data, one important question is if there is any statistically significant difference between the survival times of male and female patients diagnosed with pancreatic cancer. To answer this question, we used the non-parametric Wilcoxon rank-sum test with continuity correction and obtained a p-value of.47, which suggests that there is no statistically significant difference between the true median survival times of patients from both genders at 5% level of significance [8]. Therefore, we performed our analysis by combining the information of males and females.

3 A Brief Overview of Gradient Boosting Machine (GBM) and Extreme Gradient Boosting (XGBoost)

In the literature of machine learning, “Boosting” is a collection of algorithms that transforms the ensemble of weak learners to strong learners iteratively. Boosting is an ensemble method for improving the model predictions of any given learning algorithm. Gradient boosting machines (GBM), as introduced by Friedman (2001) [20], are a prominent family of machine-learning (ML) algorithms that have demonstrated significant success in a wide range of applied and experimental fields. They are highly customizable to the specific requirement of the application and can be implemented with respect to different loss functions. In this section, we will go through the theoretical notions of gradient boosting briefly [38].

Let us assume the problem of classical supervised learning problem where we have n risk factors $X = (x_1, x_2, \ldots , x_n)$ and y as a continuous response variable. Given the data, training of the model is performed by obtaining the optimal model parameters $\theta$ that best fit the training data $x_i$ and response $y_i$. To train the model, we define the following objective function to quantify how well the model fits the training data.

$$\begin{aligned} O(\theta ) = L(\theta ) + \varrho (\theta ) \end{aligned}$$

(1)

where $L(\theta ) = \sum _{i=1}^{n} (y_i - \hat{y_i})^2$ is the training loss (mean square error) function that measures the predictive power of our model is with respect to the training data. $\varrho (\theta )$ is the regularization term that helps to prevent model overfitting and controls the complexity of the model.

3.1 Decision Tree Ensembles

In our study, we use boosted decision tree ensemble method to train our model. Boosting combines a learning algorithm in an additive manner to achieve a strong learner from many sequentially connected weak learners. A decision tree’s major goal is to partition the input space variables into similar rectangular sections using a tree-based rule system. Each tree split corresponds to an if-then rule applied to a single input variable. A decision tree’s structure naturally stores and represents the interactions between predictor variables (risk factors). The number of splits, or equivalently, the interaction depth, is typically used to parameterize these trees. It is also possible to have one of the variables split numerous times in a row. A tree stump is a special example of a decision tree with just one split (i.e., a tree with two terminal nodes). As a result, if one wishes to fit an additive model using tree base-learners, the tree stumps can be used. Small trees and tree stumps produce remarkably accurate results in many real-world applications [49].

3.2 Model Structure

Mathematically, we can write our analytical model in the form:

$$\begin{aligned} {\hat{y}} = {\hat{f}}(x) = \sum _{i=1}^{K} {\hat{f}}_i(x),\hspace{2mm} {\hat{f}}_i \in {\mathcal {F}} \end{aligned}$$

(2)

where ${\mathcal {F}}$ is the collection of all possible regression trees, K is the number of regression trees, and ${\hat{f}}_i$ are the additive functions (additive trees) in ${\mathcal {F}}$.

$f(x) = w_{q(x)} (q:{\mathbb {R}}^m \longrightarrow \{1,2,\ldots , T\}, w \in {\mathbb {R}}^T)$. Here, q indicates the tree structure that maps an input to the relevant leaf index at which it finishes up. The number of leaves in the tree is denoted by T. Individual regression trees accommodate a continuous score on each of its leaves. $w_i$ represents the score on $i^{th}$ leaf. The tree structures of ${\hat{f}}_i$ are intractable to learn at once. Hence, we use the following additive strategy. Let $\hat{y_i}^{(t)}$ be the predicted value of the i th observation at step t. Then,

$$\begin{aligned} \begin{aligned} \hat{y_i}^{(0)}&= 0\\ \hat{y_i}^{(1)}&= {\hat{f}}_1(x_i) = \hat{y_i}^{(0)} + {\hat{f}}_1(x_i)\\ \hat{y_i}^{(2)}&= {\hat{f}}_1(x_i) + {\hat{f}}_2(x_i) = \hat{y_i}^{(1)} + {\hat{f}}_2(x_i)\\ \vdots \\ \hat{y_i}^{(t)}&= \sum _{j=1}^{t}\hat{f_j}(x_i) = \hat{y_i}^{(t-1)} + {\hat{f}}_t(x_i). \end{aligned} \end{aligned}$$

(3)

Now we have introduced the model; our goal is to define an objective function mathematically and proceed to minimize it. From Equation (1) in Section (3), we have

$$\begin{aligned} O(\theta ) = \sum _{i=1}^{n} l(y_i,\hat{y_i}) + \sum _{j=1}^{K} \varrho ({\hat{f}}_j), \end{aligned}$$

(4)

where $l(\cdot ,\cdot )$ is a convex differentiable function that measures the difference between actual $y_i$ and predicted $\hat{y_i}$. $\varrho ({\hat{f}}_j) = \gamma T + \frac{1}{2}\lambda (\mid \mid w \mid \mid )^2$. T is the number of leaves in the tree. $\gamma$ and $\lambda$ are the model hyper-parameters. From Eqs. (3) and (4), at the $t^{th}$ iteration, the objective function can be written as

$$\begin{aligned} \begin{aligned} O^{(t)}&= \sum _{i=1}^{n} l(y_i,\hat{y_i}^{(t)}) + \sum _{i=1}^{t}\varrho ({\hat{f}}_i) \\&= \sum _{i=1}^{n} l(y_i,(\hat{y_i}^{(t-1)} + {\hat{f}}_t(x_i))) + \sum _{i=1}^{t}\varrho ({\hat{f}}_i) \end{aligned} \end{aligned}$$

(5)

Since, we use the mean-square error loss function, the above equation takes the following form:

$$\begin{aligned} \begin{aligned} O^{(t)}&= \sum _{i=1}^{n} (y_i - (\hat{y_i}^{(t-1)}) + {\hat{f}}_t(x_i))^2 + \sum _{i=1}^{t}\varrho ({\hat{f}}_i)\\&= \sum _{i=1}^{n} (y_i - \hat{y_i}^{(t-1)})^2 + \sum _{i=1}^{n} ({\hat{f}}_t(x_i))^2 \\&\quad - 2\sum _{i=1}^{n}(y_i - \hat{y_i}^{(t-1)}){\hat{f}}_t(x_i) + \sum _{i=1}^{t}\varrho ({\hat{f}}_i)\\&= \sum _{i=1}^{n} (y_i - \hat{y_i}^{(t-1)})^2 + \sum _{i=1}^{n} ({\hat{f}}_t(x_i))^2 \\&\quad - 2\sum _{i=1}^{n}(y_i - \hat{y_i}^{(t-1)}){\hat{f}}_t(x_i) + \sum _{i=1}^{t-1}\varrho ({\hat{f}}_i) + \varrho ({\hat{f}}_t)\\&= \underbrace{- 2\sum _{i=1}^{n}(y_i - \hat{y_i}^{(t-1)}){\hat{f}}_t(x_i) + \sum _{i=1}^{n} ({\hat{f}}_t(x_i))^2 + \varrho ({\hat{f}}_t)}_\text {function of t} + c \end{aligned} \end{aligned}$$

(6)

where $c = \sum _{i=1}^{n} (y_i - \hat{y_i}^{(t-1)})^2 + \sum _{i=1}^{t-1}\varrho ({\hat{f}}_i)$ is a constant term (not a function of t). From the above expression, the optimal weights of the leaf can be computed which minimizes the objective function. For details, see [12, 43]. In the next section, we discuss briefly the hyper-parameters for Gradient Boosted Machines (GBMs).

3.3 Model Tuning Gradient Boosted Machine (GBM)

Although GBMs are highly flexible, they can take significant time to tune and find the optimal combination of hyperparameters. If the learning algorithm is not applied properly with the optimal combination of the hyperparameters, the model is prone to overfitting the data; this suggests that it will predict the training data rather than the functional relationship between the risk factors and response variables. The following are the most typical hyperparameters seen in most GBM implementations:

3.3.1 Number of Trees

It represents the total number of trees required to match the model. GBMs frequently necessitate a large number of trees. However, GBMs, unlike random forests, can overfit. Hence, the goal is to use cross-validation to estimate the appropriate number of trees that minimize the loss function of interest.

3.3.2 Depth of Trees

The complexity of the boosted ensemble is determined by the number of splits in each tree. It is in charge of the depth of the individual trees. Naturally, numbers range from 3 to 8; however, it is not uncommon to have a tree depth of 1 [19].

3.3.3 Shrinkage

The introduction of regularization by shrinkage is the traditional strategy to controlling model complexity. Shrinkage is employed in the context of GBMs to reduce or decrease the influence of each additionally fitted base learner. It decreases the number of incremental steps, penalizing the significance of each successive iteration. The idea behind this strategy is to take many modest steps to improve a model rather than taking a few enormous steps. If one of the boosting iterations is found to be incorrect, the adverse impact can be simply addressed in the following steps. The shrinking effect is usually denoted as the parameter $\lambda \in (0,1]$ and is applied to the final step in the gradient boosting algorithm [20, 24].

3.3.4 Subsampling

The subsampling approach has been demonstrated to increase the model’s generalization features while minimizing the required computation resources [45]. The objective of this approach is to incorporate some unpredictability into the fitting procedure. Only a random subset of the training data is used to fit a consecutive base learner at each learning iteration. Frequently, training data is sampled without replacement (SWOR). Using less than 100% of the training observations implies the implementation of stochastic gradient descent (SGD). This helps to reduce overfitting and keep the loss function gradient from being trapped in a local minimum or plateau.

Extreme Gradient Boosting (XGBoost) performs in a similar mechanism as GBM using ensemble additive training. Both XGBoost and GBM follow the principle of gradient boosting. However, XGBoost uses some more regularized model parameters to reduce overfitting and obtain the bias-variance trade-off, which improves the performance of the model.For more theoretic and practical applications, see [13, 22, 41]. In the next section, we discuss the statistical data analysis and results.

4 Statistical Analysis and Results

One of the most important goals of our study is to predict the survival times of pancreatic cancer patients with the highest degree of accuracy. For that purpose, a number of machine learning (ML) and deep learning (DL) models have been tested and validated on our data. We used Feed forward Deep Learning Models [5, 18, 46] with different layers, optimizer, and activation functions [29]. The best deep learning model that we have obtained is a dense feed-forward network with RMSE 0.38 on the test data. However, our proposed XGBoost model does the prediction task with significantly lower RMSE 0.04 on test data.

As described in Section 2.1, in our data, we have seven categorical and three numeric risk factors. Usually, most of the ML and DL algorithms do not accept categorical/factor inputs. This implies that the categorical risk factors must be converted to a numerical form. However, in our case, 70% of the risk factors are non-numeric in nature. To overcome this problem, we used a sophisticated technique, termed as “one-hot-encoding” [40]. It is a tool to convert the categorical predictors to numeric in ML algorithms to do a better job in prediction. After we convert the risk factors to a numeric scale, we perform Min-Max normalization on the set of risk factors. Min-Max normalization is a tool used in ML tasks to adjust the predictors and responses when they are in different scales. Usually, it makes all the predictors fall into [0,1]. It is defined as follows:

$$\begin{aligned} y^{*} = \frac{y - min(y)}{max(y) - min(y)} \end{aligned}$$

(7)

where y and $y^{*}$ are the original response value, and the normalized value of the response respectively. After training the XGBoost model, we can back-transform to get the original prediction of the response. In our data set, the minimum and maximum responses are 0.21 years and 21 years respectively. Hence, min(y) = 0.21 years, max(y) = 21 years, and max(y) − min(y) = (21 − 0.21) = 20.79 years. Now, we can back transform (7) in the following manner:

$$\begin{aligned} \begin{aligned} y&= min(y) + y^{*}[max(y) - min(y)]\\&= 0.21 + 20.79 y^{*} \end{aligned} \end{aligned}$$

(8)

We also performed the z-score standardization with the data but, the min-max normalization provided better performance with XGBoost. After normalizing the data, we divided the data into 70% training and 30% test data. At first, we perform the GBM algorithm on the data. In order to find the best combination of hyperparameters, we performed grid search mechanism [7, 26] that iterates through every possible combination of hyperparameter values and enables us to select the most suitable combination. To perform a grid search, we create our grid of hyper-parameter combinations. We searched across 54 models with varying learning rates (shrinkage), tree depth (interaction.depth), and the minimum number of observations allowed in the trees’ terminal nodes (n.minobsinnode). We also introduced stochastic gradient descent (SGD) in the grid search (bag.fraction < 1). The following Table 1 shows the combinations of the hyperparameters (abbreviated by S, I.D, N.M, and B.F, respectively) we used for the grid search to obtain 54 models.

Table 1 Hyper-parameters and Their Combinations in the Grid Search

We loop through each hyperparameter combination and apply the grid search on 1,000 trees. After around 30 min, our grid search completes, and we the estimated hyper-parameters for all 54 models. The following Table 2 shows top ten models (ascending order of RMSE ) with the particular choices of the hyper-parameters.

Table 2 Top 10 Models with Hyper-parameters for GBM

From the above table, we see that, while training the model, we obtain the minimum RMSE (0.03217434) for the following optimal values of the hyper-parameters in the model:

• shrinkage (S): 0.3

• interaction.depth (I.D): 5

• n.minobsinnode (N.M): 5

• bag.fraction (B.F): 0.8

• optimal_trees (O.T): 47

Now we have the optimal values of the hyper-parameters, we utilize 5-fold cross-validation to train our model with the hyper-parameters. The RMSE we obtained in the test data set using GBM is 0.04222367.

Now we proceed to perform the data analysis with XGBoost, which is more sophisticated than GBM and has more options to set the hyper-parameters to reduce overfitting. It has several hyperparameters options to train the model. We shall describe briefly the hyperparameters we used for training the model according to the definition given in the R software module [14].

• nrounds: Controls the maximum number of iterations.

• eta: Controls the learning rate, or how quickly the model learns data patterns.

• max_depth (MW): The depth of the tree is controlled by this variable. Typically, the greater the depth, the more complex the model grows, increasing the likelihood of overfitting.

• min_child_weight (MCW): It denotes the smallest number of instances required in a child node in the context of a regression problem. It aids in preventing overfitting by avoiding potential feature interactions.

• subsample (SS): It regulates the number of samples (observations) provided to a tree.

• colsample_bytree (CSBT): It controls the number of predictors given to a tree.

Similar to GBM, we perform a grid search with different combinations of hyperparameters. We trained 243 different hyper-parameter combinations to model. The following Table 3 shows top ten models (ascending order of RMSE ) with the particular choices of the hyperparameters.

Table 3 Top 10 Models with Hyper-parameters for XGBoost

From the above table, we see that the mimimum RMSE (0.0304) was achieved while training the data when

• eta = 0.05

• max_depth (MD) = 7

• min_child_weigh (MCW) = 1

• subsample (SS) = 0.8

• colsample_bytree (CSBT) = 0.8

• optimal_trees (OT) = 158

Therefore, our final XGBoost ensemble model can be expressed as follows

$$\begin{aligned} \hat{y^*} = {\hat{f}}(x) = \sum _{i=1}^{158} {\hat{f}}_i(x),\hspace{2mm} {\hat{f}}_i \in {\mathcal {F}} \end{aligned}$$

(9)

where ${\mathcal {F}}$ is the collection of all possible regression trees and ${\hat{f}}_i$ are the additive functions (additive trees) in ${\mathcal {F}}$. Our analytical model provides the best results with the optimal values of the six hyper-parameters mentioned above. With the optimal values of the hyper-parameters, we train our model with 5-fold cross-validation and obtained an RMSE of 0.04127676 in test data, which is better than what we obtained using GBM.

We can provide the algorithm to obtain the best analytical model with the optimal hyper-parameters in the following manner:

Algorithm for Obtaining Optimal Analytical Model

Input

• Input Vector: $X = (x_1, x_2,\ldots ,x_n).$

• response y as output.

• Number of iteration T decided by the researcher.

• Mean Square Error Loss Function $L(\theta ) = \sum _{i=1}^{n} (y_i - {\hat{y}}_i)$.

• Decision tree as base (weak) learner to be combined in the ensemble.

Algorithm

• for $t = 1$ to T do

  • 1. Initially, a decision tree is fitted to the data: ${\hat{f}}_1 (x) = y$.

  • 2. Next, the subsequent decision tree is fitted to the prior tree’s residuals: $d_1(x) = y - {\hat{f}}_1 (x)$

  • 3. The latest tree is then added to the algorithm: ${\hat{f}}_2 (x) = {\hat{f}}_1 (x) + d_1(x)$.

  • 4. The succeeding decision tree is fitted to the residuals of ${\hat{f}}_2: d_2(x) = y - {\hat{f}}_2 (x).$

  • 5. The new tree is then added to our algorithm: ${\hat{f}}_3 (x) = {\hat{f}}_2 + d_2(x)$

  • 6. Use cross-validation while training the model to decide the stopping criteria of the training process.

  • 7. Create a hyper-parameter grid with some user provided values and perform grid search mechanism to find optimal combination of the hyper-parameters.

  • 8. The final analytical model is the sum of all the decision tree base learners with optimal values of the hyper-parameter along with the optimal number of trees $T^*$: ${\hat{f}} = \sum _{i=1}^{T*}{\hat{f}}_i$.

• end.

4.1 Validation of the Proposed Model

After developing our proposed analytical model, it is most important to validate the model so that we can implement it to obtain the best results. In developing the model, we used 70% of the training data and obtained an RMSE of 0.034. It is a usual tendency of a good model to have a predictive performance in the test data set close to the training data set. When we implement our model on the test data set, we obtained an RMSE of.0422, which is very close to what we have obtained in the training set, implying that our model performs well on the unseen/future data set. We can predict the survival times (in years) by back-transforming the scaled response using equation (8) from Section 4 and compare how good the prediction is. The following Table 4 shows the actual and estimated predictions of pancreatic survival times (in years).

Table 4 Predicted and Actual Response

From the above table, we see that the predictions are very close to the actual response.

To validate our prediction accuracy, we also performed Wilcoxon’s rank-sum test with continuity correction to check if the actual and predicted responses are significantly different. The test produced a p-value of 0.5 (> 0.05), implying that there is insufficient sample evidence to reject the null hypothesis that both actual and predicted responses are the same. Thus, the test suggests there is no significant difference between the actual and predicted responses at a 5% level of significance.

4.2 Comparison with Different Models

The XGBoost method performed really well and was about 96% accurate. We compared the proposed boosted regression tree (using XGBoost) model with different deep-learning models to validate its performance. Deep learning models are efficient with a large amount of data to train to address the complex structure of features. We used activation functions like rectified linear unit (ReLU), Exponential Linear Unit (ELU), scaled exponential linear units (SELU), and Hyperbolic Tangent (tanh) in different layers of the deep network and used optimizer like stochastic gradient descent (SGD), Root Mean Square Propagation (RMSprop), and Adam (derived from adaptive moment estimation). In some models, we introduced dropouts and batch normalization, and in some models, we did not. Adding dropouts [21] and batch-normalization usually prevents overfitting in the networks and boosts the performance. The theoretical details and applications of the optimizer and activation functions can be found in [1, 6, 51]. Each of the models is trained using 300 epochs and batch size = 32. Table 6 compares different deep learning models in terms of root mean square error (RMSE) and mean absolute error (MAE) in the test data. In the following table, the activation function, optimizer, dropout, and batch normalization are abbreviated as AF, OPT., DROP., and BN, respectively. We considered ten deep learning sequential models with three dense layers containing units 100, 90, and 50, respectively. As Table 6 illustrates, the best deep learning model (DL6) with minimum RMSE (.378) is the model where we use tanh activation function in each of the three hidden layers, use optimizer Adam, use dropout with batch-normalization. The following Fig. 2 illustrates the graph of RMSE and MAE of DL6 while training.

Fig. 2

RMSE and MAE of DL6 for Training and Validation Data

The following Table 5 compares the boosted regression tree model using GBM and XGBoost in terms of RMSE and MAE in test data.

Table 5 Comparison of Different GBM & XGBoost Models in Terms of RMSE and MAE in Test Data

As the above Table 5 illustrates, the XGBoost performs the best with the minimum RMSE.

Table 6 Comparison of Different Deep Learning Models in Terms of RMSE and MAE in the Test Data

4.3 Ranking of Risk Factors and Prediction of the Survival Time

Once we have found the best-performing model, it is important to rank the pancreatic risk factors according to their relative importance. We rank the contributing risk factor in survival time using the measure Gain,38. The gain denotes the relative impact of a certain risk factor to the model, which is computed by considering each predictor’s contributions to each tree in the model. A higher value of this metric for a specific risk factor, compared to another risk factor, implies that the risk factor with a higher gain is more important for generating a prediction.

Fig. 3

The Relative Importance of Risk Factors Used in the XGBoost Model

From Fig. 3, we see that the top five most contributing risk factors in the model are age, current bmi, the number of years a patient smoked cigarettes, people who have family history of cancer, and people who took aspirin on a regular basis.

Table 7 illustrates the percentage contributions of the risk factors to the response survival times.

Table 7 Risk Factors and Their Percentage of Contribution to The Response

From Table 7, see that the risk factors explain 96.42% of the total variation of the response.

5 Conclusion

In cancer research, one of the most important aspects is to estimate the survival times of the patients. It results in improved management, more efficient use of resources, and the provision of specialized treatment alternatives. [4, 34]. It is imperative to investigate the clinical diagnosis and enhance the therapeutic/treatment strategy of pancreatic cancer. Pancreatic cancer is one of the deadliest cancer, and in most cases, detected in later stages (stage III /IV). Once a patient is diagnosed with pancreatic cancer, he/she or his/her family members would be interested in knowing how long is the expected/predicted survival. This question is usually asked by patients with a terminal illness to their doctors. However, it is impossible to provide the exact answer to these questions; doctors provide an answer which is mainly subjective. If we have a model based on real data that answer the questions given a particular choice of risk factors, it would be very helpful to doctors and medical professionals. Also, if we have some more relevant risk factors, we can incorporate those into this model. This would be very helpful for healthcare professionals and patients with terminal illnesses. Given a collection of risk factors, we can build a questionnaire (attached in Appendix I) that can address the patient information who are diagnosed with pancreatic cancer. Based on their response, the estimate of the survival times can be obtained very accurately. To our knowledge, there is no such model that is as accurate as our predictive analytical model. In this study,

• 1. We developed a boosted ensemble regression tree model using XGBoost that is very accurate and performs well on test data sets, given a collection of risk factors (numeric and categorical).

• 2. We ranked all the risk factors according to their relative importance in the boosted model. This ranking provides the percentage of contribution of the individual risk factors to the response and survival time.

• 3. We compared the performance of the XGBoost model with the GBM model and other ten deep-learning sequential models with different activation functions and optimizers. The XGBoost model produced an RMSE and MAE of 0.0412 and .034 which is the smallest on the test data compared to all of the other models.

• 4. The proposed analytical model can be implemented to any future data set containing information on different risk factors relating to the subject study to obtain very good predictive performance.

Appendix

In the appendix, our version of the survey questionnaire for NIH pancreatic data is posted and we request the same type of information.

1.1 Questionnaire—

• 1. panc_exitage (Numeric) ($X_1$): Age of diagnosis of the patient.

• 2. Stage (Categorical)($X_2$): Pancreatic Cancer Stages, categorized as a) localized, b) regional, and c) distant

• 3. Asp (Categorical)($X_3$): Does the person use Aspirin Regularly? “During the last 12 months, have you regularly used aspirin or aspirin containing products, such as Bayer, Bufferin or Anacin? (Please do not include aspirin-free products such as Tylenol and Panadol.)” 0=“No” 1=“Yes”

• 4. Ibup (Categorical)($X_4$): Does the person use Ibuprofen Regularly? “During the last 12 months, have you regularly used ibuprofen-containing products, such as Advil, Nuprin, or Motrin?” 0=“No” 1=“Yes”

• 5. fh_cancer (Categorical)($X_5$): The number of first-degree relatives with pancreatic cancer. Any first-degree relative with cancer. 0=“No” 1=“Yes”

• 6. Sex ($X_6$): Sex of the individual. 1=“Male” 2=“Female”

• 7. BMI (numeric)($X_7$): Current Body Mass Index (BMI) at Baseline (In lb/in2)

• 8. Cigarette Years (numeric)($X_8$): The total number of years the patient smoked.

• 9. gallblad_f (Categorical)($X_9$): Did the individual ever have gallbladder stones or inflammation? 0=“No” 1=“Yes”

• 10. hyperten_f (Categorical)($X\_{10}$): Did the individual ever have high blood pressure? 0=“No” 1=“Yes”