1 Introduction

The logistic distribution has been found several applications in various fields such as public health (Grizzle [8]), survival analysis (Plackett [13]), biology (Pearl and Reed [12]), bioassay problems (Berkson [3,4,5]) etc. For a detailed account of properties and applications of various forms of logistic distributions, refer Balakrishnan [1]. Several generalised distributions have been studied in the literature. Balakrishnan and Leung [2] studied three types of generalized logistic distributions. Wahed and Ali [18] introduced the skew logistic distribution (SLD). An extension of SLD was proposed by Nadarajah [11]. A flexible class of skew logistic distribution was studied by Kumar and Manju [10].

A continuous random variable X is said to have the standard logistic distribution (LD) if its probability density function (PDF) is of the following form, for \(x\in R=\left( -\infty ,+\infty \right)\).

$$\begin{aligned} f_1\left( x \right) =\frac{{e^{-x} }}{{\left( {1 + e^{-x} } \right) ^2 }}. \end{aligned}$$
(1)

The cumulative distribution function (CDF), \(F_{1}(.)\) of the LD is

$$\begin{aligned} F_1\left( x \right) =\frac{1}{{1 + e^{ - x} }}, \end{aligned}$$
(2)

for \(x\in\) R. Balakrishnan and Leung [2] introduced and studied two generalized classes of logistic distributions namely the generalized logistic distribution of type I \((denoted\; by \;LD_{I})\) and type II \((denoted\; by\; LD_{II})\) respectively through the following PDFs \(f_2 \left( {.} \right)\) and \(f_3 \left( {.} \right)\), for \(x\in R\), \(\alpha > 0\) and \(\beta >0\).

$$\begin{aligned}&f_2 \left( {x,\alpha ,\beta } \right) =\alpha \beta \frac{{ e^{ - \beta x} }}{{\left( {1 + e^{ - \beta x} } \right) ^{\alpha + 1} }} \end{aligned}$$
(3)
$$\begin{aligned} &f_3 \left( {x,\alpha } \right) =\frac{{\alpha e^{ - \alpha x} }}{{\left( {1 + e^{ - x} } \right) ^{\alpha + 1} }} \end{aligned}$$
(4)

The CDFs corresponds to the \(LD_{I}\) and the \(LD_{II}\) are respectively

$$\begin{aligned} F_2\left( x \right) =\frac{1}{{\left( {1 + e^{ - \beta x} } \right) ^{\alpha } }} \end{aligned}$$
(5)

and

$$\begin{aligned} F_3\left( x \right) =1 - \frac{{e^{ - \alpha x} }}{{\left( {1 + e^{ - x} } \right) ^\alpha }}. \end{aligned}$$
(6)

Clearly, when \(\alpha =\beta =1\) in (5), the CDF of \(LD_{I}\) reduces to that of the LD and when \(\alpha =1\) in (6), the CDF of \(LD_{II}\) reduces to that of the LD. Both these classes of distributions have applications in several areas of scientific research. Through the present paper we attempt to unify both these classes of distributions and termed it as “the gamma generalized logistic distribution (GGLD)”, which is not available any where in the existing literature . The objective of the present work is to develop a more flexible class of distribution which can handle asymmetric distributions and derive some of its important properties. The paper is organized as follows. In Sect. 2, we present the definition of the GGLD and describe some important properties. A location scale extension of the GGLD is considered in Sect. 3 and in Sect. 4, two real life medical data sets are considered for illustrating the usefulness of the model compared to the LD, \(LD_{I}\) and \(LD_{II}\). In Sect. 5, a generalized likelihood ratio test procedure is suggested for testing the significance of the parameters of the GGLD and a simulation study is conducted to test the efficiency of the maximum likelihood estimators (MLEs) of the distribution in Sect. 6 . We have the following representations from Gradshteyn and Ryzhik [7] , those we need in the sequel.

  1. (i)

    For \({Re (\mu )\; > - 1},\)

    $$\begin{aligned} \quad \int \limits _0^1 {x^{\mu - 1} \ln \left( {1 - x} \right) } dx =- \frac{1}{\mu }\left[ {\psi \left( {\mu + 1} \right) -\psi (1)} \right] =- \frac{1}{\mu }\left[ {\psi \left( {\mu + 1} \right) +C} \right] , \end{aligned}$$
    (7)

    in which \(\Psi \left( a \right) = \frac{{d\log \Gamma a}}{{da}}\) and C is the Euler’s constant.

  2. (ii)

    For \(u^2 < 1,\)

    $$\begin{aligned} \left[ {\ln \left( {1 - u} \right) } \right] ^2 =2 \sum \limits _{j = 1}^\infty {\frac{{ u^{j + 1} }}{{j + 1}}} \sum \limits _{i = 1}^j {\frac{1}{i}} \end{aligned}$$
    (8)

2 Definition and Properties

In this section, first we present the definition of the GGLD and discuss some of its important properties. A continuous random variable X is said to follow gamma generalized logistic distribution if its CDF is of the following form, in which \(x\in R\) , \(\alpha > 0\), \(\gamma > 0\) and \(\beta > 0\).

$$\begin{aligned} F(x)=1 - \left[ {1 - \frac{1}{{(1 + e^{-\beta x} )^\alpha }}} \right] ^\gamma \end{aligned}$$
(9)

On differentiating (9) with respect to x, we have the probability density function (PDF) of GGLD as

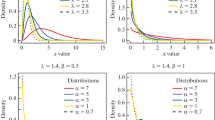
$$\begin{aligned} f\left( {x; \,\alpha ,\beta ,\gamma } \right) = \alpha \beta \gamma \frac{{e^{ - \beta x} }}{{(1 + e^{-\beta x} )^{\alpha + 1} }}\left[ {1 - \frac{1}{{(1 + e^{ -\beta x} )^\alpha }}} \right] ^{\gamma - 1} . \end{aligned}$$
(10)

The distribution of a random variable with CDF (9) or PDF (10) is hereafter we denoted by \(GGLD\left( \alpha , \beta , \gamma \right)\). Clearly, when \(\gamma =1\), the GGLD reduces to the \(LD_{I}\) and when \(\alpha =\beta =1\), the GGLD reduces to \(LD_{II}\) with parameter \(\gamma .\) The PDF plots of \(GGLD\left( \alpha , \beta ,\gamma \right)\) for particular choices of its parameters \(\alpha , \beta\) and \(\gamma\) is given in Fig. 1. From the figure it is clear that for fixed \(\alpha\) and \(\beta\), the distribution is positively skewed for \(\gamma < 1\) and negatively skewed for \(\gamma > 1\). Furthermore, as \(\gamma\) increases the kurtosis is also increases for fixed \(\alpha\) and \(\beta\).

Proposition 1

The characteristic function \(\Phi _X \left( t \right)\) of \(GGLD\left( \alpha , \beta ,\gamma \right)\) with PDF (10) is the following, for \(t\in R\), where B(.,.) is the beta function.

$$\begin{aligned} \Phi _X \left( t \right) = \alpha \gamma \sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k } \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) B\left( {\alpha +\alpha k + \frac{it}{\beta },\;1 - \frac{it}{\beta }} \right) \end{aligned}$$
(11)

Proof

Let X follows \(GGLD\left( \alpha , \beta ,\gamma \right)\) with PDF (10). Then by the definition of characteristic function, we have the following for any \(t\in R\) and i=\(\sqrt{-1}\).

$$\begin{aligned} \Phi _X \left( t \right) =\int \limits _{ - \infty }^\infty {e^{itx} \alpha \beta \gamma \frac{{e^{ -\beta x} }}{{\left( {1 + e^{ -\beta x} } \right) ^{\alpha + 1} }}} \left[ {1 - \frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right] ^{\gamma - 1} dx \end{aligned}$$
(12)

substitute \(\frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^{\alpha + 1} }} = u\) in (12), to obtain

$$\begin{aligned} \Phi _X \left( t \right) = \alpha \gamma \int _0^1 {u^{\frac{{it}}{\beta } + \alpha - 1} \left( {1 - u} \right) ^{\frac{{ - it}}{\beta }} } \left( {1 - u^\alpha } \right) ^{\gamma - 1} du. \end{aligned}$$
(13)

Now applying binomial expansion of \(\left( 1- u^\alpha \right) ^{\gamma - 1}\) in (13) and rearranging the terms to get the following.

$$\begin{aligned} \Phi _X \left( t \right) = \alpha \gamma \sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k }\left( {\begin{array}{c}{\gamma -1}\\ k\end{array}}\right) \int \limits _0^1 {u^{\frac{{it}}{\beta } + \alpha k + \alpha - 1} } \left( {1 - u} \right) ^{^{\frac{{ - it}}{\beta }} } du, \end{aligned}$$
(14)

which gives (11), by the definition of beta integral. \(\square\)

Proposition 2

The mean and variance of \(GGLD\left( \alpha , \beta ,\gamma \right)\) with PDF (10) are respectively

$$\begin{aligned} Mean & =\frac{{\alpha \gamma }}{\beta }\sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k } \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) \eta _{k,\alpha }(0)\left[ { {\psi \left( {\eta _{k,\alpha }^{-1}(1)} \right) -\psi (1) } - \eta _{k,\alpha }(0)} \right] \nonumber \\ & =\Lambda \left( {\alpha ,\beta ,\gamma } \right) ,say\;\;\;\; \end{aligned}$$
(15)

and

$$\begin{aligned} Variance = \frac{{2\alpha \gamma }}{{\beta ^2 }}\sum \limits _{k = 0}^\infty {\sum \limits _{j = 1}^\infty {\sum \limits _{i = 1}^j {\left( { - 1} \right) ^k } } } \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) \left[ {\eta _{k,\alpha }^3 (0)} \right. + \eta _{k,\alpha } (0)\eta _{k,\alpha }^2 (j) - \nonumber \\ \quad \quad \quad \left. {\left( {\psi (\eta _{k,\alpha }^{ - 1} (1)) - \psi (1)} \right) \eta _{k,\alpha }^2 (0) + \frac{{\eta _{k,\alpha } (j + 1)}}{{i(j + 1)}}} \right] - \Lambda ^2 (\alpha ,\beta ) \end{aligned}$$
(16)

where \(\eta _{k,\alpha }(a) = (\alpha + \alpha k + a)^{-1}\) and \(\psi \left( a \right)\) is as defined in (7).

Proof

By definition, the mean of \(GGLD\left( \alpha , \beta ,\gamma \right)\) is

$$\begin{aligned} \mu '_1 & = \alpha \beta \gamma \int \limits _{ - \infty }^\infty x \frac{{1}}{{\left( {1 + e^{ -\beta x} } \right) ^{\alpha + 1} }}\left[ {1 - \frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right] ^{\gamma - 1} dx \\ & = \frac{\alpha \gamma }{\beta } \int \limits _0^1 {\ln \left( {\frac{u}{{1 - u}}} \right) } \;u^{\alpha - 1} \left( {1 - u^\alpha } \right) ^{\gamma - 1} du, \end{aligned}$$

by putting \(u=\left( {1 + e^{ - \beta x} } \right) ^{ - 1}.\) Now by binomial expansion of \(\left( {1 - u^\alpha } \right) ^{\gamma - 1}\), we obtain the following.

$$\begin{aligned} \mu '_1 & = \frac{{\alpha \beta }}{\gamma }\sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k } \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) \left( {\int \limits _0^1 {u^{\alpha + \alpha k - 1} } } \right. \ln (u)du \nonumber \\&\quad - \left. {\int \limits _0^1 {u^{\alpha + \alpha k - 1} \ln (1 - u)du} } \right) \end{aligned}$$
(17)

Applying (7) in the second integral term of (17) and by using integration by parts in the first integral term, one can obtain (15).

By definition, the variance of \(GGLD\left( \alpha , \beta ,\gamma \right)\) gamma generalized logistic distribution (GGLD) is

$$\begin{aligned} Variance=\int \limits _{ - \infty }^\infty {x^2 } f\left( x \right) dx-\Lambda ^2 \left( {\alpha ,\beta } \right) , \end{aligned}$$
(18)

in which

$$\begin{aligned} \int \limits _{ - \infty }^\infty {x^2 } f\left( x \right) dx & = \alpha \beta \gamma \int \limits _{ - \infty }^\infty x^2 \frac{{e^{ -\beta x} }}{{\left( {1 + e^{ -\beta x} } \right) ^{\alpha + 1} }}\left[ {1 - \frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right] ^{\gamma - 1} dx \nonumber \\ & = \frac{\alpha \gamma }{\beta ^2} \int \limits _0^1 {\left[ {\ln \left( { u} \right) - \left( {1 - u} \right) } \right] } ^2 u^{\alpha - 1} \left( {1 - u^\alpha } \right) ^{\gamma - 1} du, \end{aligned}$$
(19)

by taking \(u = \frac{{1 }}{{1 + e^{ -\beta x} }}\). By applying binomial expansion of \(\left( {1 - u^\alpha } \right) ^{\gamma - 1}\), in (19), we obtain the following.

$$\begin{aligned} \int \limits _{ - \infty }^\infty {x^2 } f\left( x \right) dx & = \frac{\alpha \gamma }{\beta ^2}\; \sum \limits _{k = 0}^\infty \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) \left( { - 1} \right) ^k \int \limits _0^1 {\left[ {\ln \left( { u} \right) - \ln \left( {1 - u} \right) )} \right] ^2 u^{\alpha + \alpha k - 1} } du\nonumber \\ & = \frac{\alpha \gamma }{\beta ^2}\sum \limits _{k = 0}^\infty \left( {\begin{array}{c}\gamma -1\\ k\end{array}}\right) \left( { - 1} \right) ^k \left[ {I_1 + I_2 + I_3 } \right] , \end{aligned}$$
(20)

where

$$\begin{aligned} I_1 =\int \limits _0^1 {\left[ {\ln \left( u \right) } \right] ^2 u^{\alpha + \alpha k - 1} } du, \end{aligned}$$
(21)
$$\begin{aligned} I_2 =-2\int \limits _0^1 {\ln \left( u \right) \ln \left( {1 - u} \right) u^{\alpha + \alpha k - 1} } du \end{aligned}$$
(22)

and

$$\begin{aligned} I_3=\int \limits _0^1 {\left[ {\ln \left( {1 - u} \right) } \right] } ^2 u^{\alpha + \alpha k - 1} du. \end{aligned}$$
(23)

Now, by using integration by parts we have the following from (21).

$$\begin{aligned} I_1 & = \frac{2}{{\left( {\alpha + \alpha k} \right) ^3 }} \nonumber \\ & = 2\eta ^3 _{k,\alpha }(0) \end{aligned}$$
(24)

In a similar way, we obtain the following from (22).

$$\begin{aligned} I_2 & = 2\left( \sum \limits _{j = 1}^\infty {\frac{1}{{\left( {\alpha + \alpha k} \right) \left( {\alpha + \alpha k + j} \right) ^2 }}} - \frac{{\psi \left( {\alpha + \alpha k + 1} \right) - \psi \left( 1 \right) }}{{\left( {\alpha + \alpha k} \right) ^2 }}\right) \nonumber \\ & = 2\left( \sum \limits _{j = 1}^\infty {\eta _{k,\alpha }(0) } \eta ^2 _{k,\alpha }({j}) - \left( {\psi \left( {\eta _{k,\alpha }^{-1}(1) } \right) -\psi (1)} \right) \eta _{k,\alpha }(0) ^2\right) \end{aligned}$$
(25)

Applying (8) in (23), \(I_3\) becomes,

$$\begin{aligned} I_3 & = 2\sum \limits _{j = 1}^\infty {\sum \limits _{i = 1}^j {\frac{1}{{i\left( {j + 1} \right) \left( {\alpha + \alpha k + j + 1} \right) }}} } \nonumber \\ & = 2 \sum \limits _{j = 1}^\infty {\sum \limits _{i = 1}^j {\frac{{\eta _{k,\alpha }{{(j + 1)} }}}{{i\left( {j + 1} \right) }}} }. \end{aligned}$$
(26)

Thus, from (18) and (20) we get (16), in the light of (24), (25) and (26). \(\square\)

Proposition 3

The quantile of \(GGLD\left( \alpha , \beta ,\gamma \right)\) of order c, \(X_{c}\) is given by

$$\begin{aligned} X_c = - \frac{1}{\beta }\ln \left[ {\left( {1 - \left( {1 - c } \right) ^{1/\gamma } } \right) ^{ - 1/\alpha } - 1} \right] \end{aligned}$$
(27)

Proof

By inverting (9), one can obtain (27). \(\square\)

Proposition 4

Measure of skewness \(g_a\) and kurtosis \(L_0\) of \(GGLD\left( \alpha , \beta ,\gamma \right)\) with PDF (10) are given by

$$\begin{aligned} g_a = \log \left( {\frac{{\delta _{0.5} }}{{\delta _{0.2} }}} \right) \left[ {\log \left( {\frac{{\delta _{0.8} }}{{\delta _{0.5} }}} \right) } \right] ^{ - 1} \end{aligned}$$
(28)

and

$$\begin{aligned} L_0 = \log \left( {\frac{{\delta _{0.975} }}{{\delta _{0.025} }}} \right) \left[ {\log \left( {\frac{{\delta _{0.75} }}{{\delta _{0.25} }}} \right) } \right] ^{ - 1}, \end{aligned}$$
(29)

in which \(\delta _c = [(1 - c^{1/\gamma } )^{-1/\alpha } -1]\).

Proof

Galton [6] introduced the percentile oriented measure of skewness as

$$\begin{aligned} g_a = \frac{{x_{0.8} - x_{0.5} }}{{x_{0.5} - x_{0.2} }}, \;\; \;\; \end{aligned}$$
(30)

so that \(0< g_a <\infty\). Note that \(g_a=1\) indicates symmetry, \(g_a<1\) indicates skewness to left while \(g_a>1\) is interpreted as skewness to right. Schmid and Trede [17] defined the percentile oriented measure of kurtosis \(L_0\) as the product of the measure of tail \(T =\frac{{x_{0.975} - x_{0.025} }}{{x_{0.875} - x_{0.125} }}\) and the measure of peakedness \(P =\frac{{x_{0.875} - x_{0.125} }}{{x_{0.75} - x_{0.25} }}\) . That is,

$$\begin{aligned} L_0 =\frac{{x_{0.975} - x_{0.025} }}{{x_{0.75} - x_{0.25} }}. \end{aligned}$$
(31)

Now the proof of (28) and (29) follows form (27), (30) and (31). It is quite interest to note that both skewness and kurtosis depends only on \(\alpha\) and \(\gamma\). From Appendix it is clear that the the skewness of this distribution ranges from 0.67 to 1.82. From Fig. 1 also it is evident that this is a moderately skewed distribution. The computed values of skewness and kurtosis for different values of the parameters are given in Appendix . \(\square\)

Proposition 5

The PDF of the kth order statistics \(X_{k:n}\) of \(GGLD\left( \alpha , \beta ,\gamma \right)\) is

$$\begin{aligned} f_{k:n} \left( x \right) & = \frac{{\alpha \beta \gamma }}{{B\left( {k,\;n - k + 1} \right) }}\frac{{e^{ -\beta x} }}{{\left( {1 + e^{ - \beta x} } \right) ^{\alpha + 1} }}\left[ {1 - \frac{{1}}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right] ^{ n +\gamma -k-1 } \nonumber \\& \quad \times \left[ {1 - \left( {1 - \frac{{1 }}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right) ^\gamma } \right] ^{k - 1}. \end{aligned}$$
(32)

Proof

Let \(X_{1},X_{2}, ...,X_{n}\) be a random sample of size n from the \(GGLD\left( \alpha , \beta ,\gamma \right)\) and let \(X_{k:n}\) be the \(k^{th}\) order statistic for k = 1, 2, ..., n. Let \(F_{x_{k:n}}(x)\) and \(f_{x_{k:n}}(x)\) denotes the CDF and the PDF of \(X_{k:n}\) respectively. Then

$$\begin{aligned} f_{k:n} \left( x \right) = \frac{1}{{B\left( {k,n - k + 1} \right) }}\left[ {F\left( x \right) } \right] ^{k - 1} \left[ {1 - F\left( x \right) } \right] ^{n - k} f\left( x \right) \end{aligned}$$
(33)

for \(x\in\) R. Now, by applying (9) and (10) in (33) to obtain (32). \(\square\)

From Proposition (5), we have the following Corollaries.

Corollary 1

The distribution of the smallest order statistic \(X_{1:n}\) based on a random sample of size n taken from a population following \(GGLD\left( \alpha , \beta ,\gamma \right)\) is \(GGLD\left( \alpha , \beta ,n\gamma \right)\).

Corollary 2

The PDF of the largest order statistics \(X_{n:n}\) is

$$\begin{aligned} f_{n:n} \left( x \right) & = n\alpha \beta \gamma \frac{{e^{ - \beta x} }}{{\left( {1 + e^{ -\beta x} } \right) ^{\alpha + 1} }}\left[ {1 - \frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right] ^{\gamma - 1}\nonumber \\&\times \left[ {1 - \left( {1 - \frac{1}{{\left( {1 + e^{ -\beta x} } \right) ^\alpha }}} \right) ^\gamma } \right] ^{n - 1}, \end{aligned}$$
(34)

for x \(\in\) R, which reduces to \(LD_{I}\left( \alpha n, \beta \right)\) when \(\gamma =1\).

Proposition 6

The Renyi entropy of \(GGLD\left( \alpha , \beta ,\gamma \right)\) is given by

$$\begin{aligned} \begin{array}{l} I_R \left( \theta \right) = \frac{1}{{1 - \theta }}\left\{ {\theta \ln \left( {\alpha \beta \gamma } \right) - \ln \left( \beta \right) } \right. \\ \quad \quad \quad \quad \quad \;\;\;\left. + {\ln \left[ {\sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k \left( {\begin{array}{c}\gamma \theta -\theta \\ k\end{array}}\right) B\left( {\alpha k + \alpha \theta ,\theta } \right) } } \right] } \right\} \\ \end{array} \end{aligned}$$
(35)

Proof

For \(0< \theta \ne 1\) the Renyi entropy \(I_R \left( \theta \right)\) is defined as

$$\begin{aligned} \begin{array}{l} I_R \left( \theta \right) = \frac{1}{{1 - \theta }}\ln \left\{ {\int {f^\theta \left( x \right) dx} } \right\} \\ = \frac{1}{{1 - \theta }}\ln \left\{ {\left( {\alpha \beta \gamma } \right) ^\theta \int {\left( {\left( {\frac{{e^{ - \beta x} }}{{1 + e^{ - \beta x} }}} \right) ^\theta } \right. } \frac{1}{{\left( {1 + e^{ - \beta x} } \right) ^{\alpha \theta } }}} \right. \\ \quad \left. \times {\left( {1 - \frac{1}{{\left( {1 + e^{ - \beta x} } \right) ^\alpha }}} \right) ^{\theta \left( {\gamma - 1} \right) } dx} \right) \\ \end{array} \end{aligned}$$
(36)

On substituting \(\frac{1}{{1 + e^{ - x} }}\; = u\) in (36) we have

$$\begin{aligned} I_R \left( \theta \right) & = \frac{1}{{1 - \theta }}\ln \left\{ {\frac{\left( {\alpha \beta \gamma } \right) ^\theta }{\beta } \int \limits _0^1 {u^{\alpha \theta - 1} \left( {1 - u} \right) ^{\theta - 1} } \left( {1 - u^\alpha } \right) ^{\theta \left( {\gamma - 1} \right) } du} \right\} \nonumber \\ & = \frac{1}{{1 - \theta }}\ln \left\{ {\frac{\left( {\alpha \beta \gamma } \right) ^\theta }{\beta } \sum \limits _{k = 0}^\infty {\left( -1\right) ^k }\left( {\begin{array}{c}\gamma \theta -\theta \\ k\end{array}}\right) \int \limits _0^1 {u^{\alpha \theta +\alpha k - 1} \left( {1 - u} \right) ^{\theta - 1} } du} \right\} , \end{aligned}$$

by applying binomial expansion in \(\left( {1 - u^\alpha } \right) ^{\theta \left( {\gamma - 1} \right) }.\) Thus we have

$$\begin{aligned} I_R \left( \theta \right) = \frac{1}{{1 - \theta }}\ln \left\{ {\frac{{\left( {\alpha \beta \gamma } \right) ^\theta }}{\beta }\sum \limits _{k = 0}^\infty {\left( { - 1} \right) ^k \left( {\begin{array}{c}\gamma \theta -\theta \\ \theta \end{array}}\right) B\left( {\alpha k + \alpha \theta ,\theta } \right) } } \right\} \end{aligned}$$
(37)

which gives (35). \(\square\)

Proposition 7

The survival function is given by

$$\begin{aligned} S(x) = \left[ {1 - \frac{1}{{\left( {1 + e^{ - \beta x} } \right) ^\alpha }}} \right] ^\gamma \end{aligned}$$

Proposition 8

The hazard function is given by

$$\begin{aligned} h(x) = \frac{{\alpha \beta \gamma }}{{\left( {1 + e^{\beta x} } \right) \left[ {\left( {1 + e^{ - \beta x} } \right) ^\alpha - 1} \right] }} \end{aligned}$$

The proof follows directly from the definition of survival function and hazard function and hence, omitted. The curve of hazard function is given in Fig.  2. From the curve it is seen that when \(\alpha , \beta \; \text {and} \; \; \gamma\) are more than 1, the curve has a point of inflection between 0.5 and 1 , and thereafter it remains stable. The point of inflection increases as any one of the parameters takes a value less than one.

3 Location Scale Extension

In this section we define an extended form of \(GGLD\left( \alpha ,\; \beta ,\;\gamma \right)\) by introducing the location parameter \(\mu\) and scale parameter \(\sigma\) and discuss the maximum likelihood estimation of the parameters of extended form of \(GGLD\left( \alpha ,\; \beta ,\;\gamma \right)\).

Definition

Let Z follows the \(GGLD\left( \alpha , \;\beta ,\; \gamma \right)\) with PDF (10). Then \(X = \mu +\;\sigma Z\) is said to have an “extended GGLD with parameters \(\mu ,\; \sigma ,\; \alpha ,\;\beta\) and \(\gamma\)”, denoted by “\(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\)”. The PDF of \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) is

$$\begin{aligned} f\left( {x;\mu ,\sigma , \alpha ,\beta ,\gamma } \right) & = \alpha \beta \gamma \frac{{e^{ - \beta \left( {\frac{{x - \mu }}{\sigma }} \right) } }}{{\sigma \left( {1 + e^{ - \beta \left( {\frac{{x - \mu }}{\sigma }} \right) } } \right) ^{\alpha + 1} }}\nonumber \\&\times \left( {1 - \frac{1}{{\left( {1 + e^{ - \beta \left( {\frac{{x - \mu }}{\sigma }} \right) } } \right) ^\alpha }}} \right) ^{\gamma - 1} \end{aligned}$$
(38)

in which \(x\in R\), \(\mu \in R\), \(\alpha> 0,\; \beta > 0\) and \(\gamma >0\). Next we discuss the maximum likelihood estimation of \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\). Let \(X_{1},\; X_{2},\; .\; .\; .\; ,X_{n}\) be a random sample from a population having \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) with the PDF (38). Let \(L (\mu ,\;\sigma ;\;\alpha \; ,\beta ,\;\gamma )\) denote the likelihood function, the log-likelihood function \(l = \ln L (\mu ,\;\sigma ;\;\alpha ,\;\beta ,\;\gamma )\) of the random sample is

$$\begin{aligned} l & = n\ln \alpha + n\ln \beta + n\ln \gamma - n\ln \sigma - \beta \sum \limits _{i = 1}^n {\frac{{\left( {x_i - \mu } \right) }}{\sigma }} - \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\ln \left( {1 + e^{ - \beta \left( {\frac{{x_i - \mu }}{\sigma }} \right) } } \right) } \nonumber \\&+\left( {\gamma - 1} \right) \sum \limits _{i = 1}^n {\ln } \left( {1 - \frac{1}{{\left( {1 + e^{ - \beta \left( {\frac{{x_i - \mu }}{\sigma }} \right) } } \right) ^\alpha }}} \right) \;\;\;\; \end{aligned}$$
(39)

On differentiating (39) with respect to parameters \(\mu ,\; \sigma ,\; \alpha ,\; \beta ,\; \gamma\) and equating to zero, we obtain the following likelihood equations, in which \(z_i = \frac{{x_i - \mu }}{\sigma }\), for each i = 1, 2, . . . , n and \(\Omega _j = \left[ {1 + e^{-\beta \left( {\frac{{x_i - \mu }}{\sigma }} \right) } } \right] ^j\), for j=1 or \(\alpha\).

$$\begin{aligned} n\beta = \beta \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\frac{{e^{ - \beta z_i } }}{{\Omega _1 }}} + \alpha \beta \left( {\gamma - 1} \right) \sum \limits _{i = 1}^n {\frac{{e^{ - \beta z_i } }}{{\Omega _1 \left( {\Omega _\alpha - 1} \right) }}} \end{aligned}$$
(40)
$$\begin{aligned} n = \beta \sum \limits _{i = 1}^n {z_i } - \beta \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\frac{{z_i e^{ - \beta z_i } }}{{\Omega _1 }}} + \alpha \beta \left( {\gamma - 1} \right) \sum \limits _{i = 1}^n {\frac{{z_i e^{ - \beta z_i } }}{{\Omega _1 \left( {\Omega _\alpha - 1} \right) }}} \end{aligned}$$
(41)
$$\begin{aligned} \frac{n}{\alpha } = \sum \limits _{i = 1}^n {\ln } \left( {\Omega _1 } \right) + \left( {\gamma - 1} \right) \sum \limits _{i = 1}^n {\frac{{\ln \left( {\Omega _1 } \right) }}{{\left( {\Omega _\alpha - 1} \right) }}} \end{aligned}$$
(42)
$$\begin{aligned} \frac{n}{\beta } = \sum \limits _{i = 1}^n {z_i } - \left( {\alpha + 1} \right) \sum \limits _{i = 1}^n {\frac{{z_i e^{ - \beta z_i } }}{{\Omega _1 }}} + \alpha \left( {\gamma - 1} \right) \sum \limits _{i = 1}^n {\frac{{z_i e^{ - \beta z_i } }}{{\Omega _1 \left( {\Omega _\alpha - 1} \right) }}} \end{aligned}$$
(43)
$$\begin{aligned} \frac{n}{\gamma } = \sum \limits _{i = 1}^n {\ln \left( {1 - \Omega _{^\alpha }^{ - 1} } \right) } \end{aligned}$$
(44)

When these likelihood equations donot always have solutions, the maximum of the likelihood function is reached at the border of the parameter domain. Since the MLE of the unknown parameters \(\mu ,\; \sigma ,\; \alpha ,\; \beta ,\; \gamma\) cannot be obtained in closed forms, there is no way to derive the exact distribution of the MLE. Therefore, we derived the second order partial derivatives of the log-likelihood function with respect to the parameters \(\mu ,\; \sigma ,\; \alpha ,\; \beta ,\; \gamma\) using MATHLAB software and noticed that these gave negative values for \(\mu>0,\; \sigma>0,\;\alpha>0,\; \beta>0,\; \gamma >0\). Hence the maximum likelihood estimators of the parameters of \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) can be obtained by solving the above system of Eqs. (40)–(44) with the help of mathematical softwares such as MATLAB, MATHCAD, MATHEMATICA, R etc.

4 Applications

For numerical illustration we consider the following two data sets .

Data set 1. Myopia Data data set available in “https://www.umass.edu//statdata”. This data set is also used by Hosmer et al. [9]. The dataset is a subset of data from the Orinda Longitudinal Study of Myopia (OLSM), a cohort study of ocular component development and risk factors for the onset of myopia in children. Data collection began in the 1989–1990 school year and continued annually through the 2000–2001 school year. All data about the parts that make up the eye (the ocular components) were collected during an examination during the school day. Data on family history and visual activities were collected yearly in a survey completed by a parent or guardian. The dataset used in this text is from 618 of the subjects who had at least 5 years of follow-up and were not myopic when they entered the study. All data are from their initial exam and the dataset includes 17 variables. We have taken the continuous variable vitreous Chamber depth (VCD) in mm of 618 patients. VCD is the length from front to back of the aqueous-containing space of the eye in front of the retina.

Data set 2. Rosner’s FEV Data set available in “http://biostat.mc.vanderbilt.edu//DataSets". The data set contains determinations of forced expiratory volume (FEV) on 654 subjects in the age group of 6–22 years who were seen in the childhood respiratory disease study in 1980 in East Boston, Massachusetts. Forced expiratory volume (FEV), a measure of lung capacity, is the variable of interest. We obtain the maximum likelihood estimators (MLEs) of the parameters of the \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) by using the ‘nlm()’ package in R software. The values of Kolmogrov–Smirnov Statistic (KSS), Akaike information criterion (AIC), Bayesian information criterion \(\left( BIC \right)\), Consistent Akaike information criterion \(\left( CAIC \right)\) and Hannan Quinn information criterion \(\left( HQIC \right)\) are computed for comparing the model \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) with the existing logistic models—\(LD(\mu ,\sigma )\), \(LD_{ I}(\mu ,\sigma ,\alpha ,\beta )\), \(LD_ {II} (\mu ,\sigma ,\alpha )\). Moreover, the distribution is compared with another family of distribution, double lindely distribution (DLD) of Kumar and Jose [16] having distribution function

$$\begin{aligned} f\left( {x,\theta } \right) = \frac{{\theta ^2 }}{{2(1 + \theta )}}\left( {1 + \left| x \right| } \right) e^{ - \theta \left| x \right| } \end{aligned}$$

\(x\in R=\left( -\infty , +\infty \right) \,\,and\;\;\theta > 0\)

From Table 1, it is seen that the KSS, AIC, BIC, CAIC and HQIC values are minimum for \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) compared to other models. Figures  3 and 4 also confirm this result. These observations reveals that the \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) is relatively a better model compared to the existing models.

5 Testing of Hypothesis

In this section we discuss certain generalized likelihood ratio test procedures for testing the parameters of the \(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\) and attempt a brief simulation study. Here we consider the following tests. Test 1. \(H_{01}:\gamma = 1\) against \(H_{11} :\gamma \ne 1\) Test 2. \(H_{02}:\alpha =1,\; \beta = 1\) against \(H_{12} :\alpha \ne 1,\; \beta \ne 1\) Test 3. \(H_{03}:\alpha = 1,\; \beta = 1,\; \gamma = 1\) against \(H_{13}:\alpha \ne 1, \; \beta \ne 1, \; \gamma \ne 1\) In this case, the test statistic is,

$$\begin{aligned} - 2\ln \Lambda = 2\left[ {\ln L( {\mathop \Omega \limits ^ \wedge ;y|x}) - \ln L( {\mathop \Omega \limits ^{ \wedge * } ;y|x})} \right] , \end{aligned}$$
(45)

where \(\mathop \Omega \limits ^ \wedge\) is the maximum likelihood estimator of \(\Omega = \left( {\mu ,\;\sigma ,\;\alpha ,\;\beta ,\;\gamma } \right)\) with no restriction, and \(\mathop \Omega \limits ^{ \wedge * }\) is the maximum likelihood estimator of \(\Omega\) when \(\gamma = 1\) in case of Test 1, \(\alpha = 1,\; \beta = 1\) in case of Test 2 and \(\alpha = 1,\;\beta =1,\; \gamma =1\) in case of Test 3 respectively. The test statistic \(- 2\ln \Lambda\) given in (45) is asymptotically distributed as \(\chi ^{2}\) with one degree of freedom for test 1, 2 degree of freedom for test 2 and 3 degree of freedom for test 3 [14]. The computed values of \(lnL( {\mathop \Omega \limits ^ \wedge ;y|x}), \;ln L( {\mathop \Omega \limits ^{ \wedge * } ;y|x})\) and test statistic in case of the two data sets are listed in Table  2. Since the critical values at the significance level 0.05 and degree of freedom one, two and three for the two tailed test are 5.024, 7.378 and 9.348 respectively the null hypothesis is rejected in all cases, which shows the appropriateness of the EGGLD to both the data sets.

6 Simulation

To assess the performance of the estimates of the parameters of

\(EGGLD\left( \mu ,\;\sigma ;\;\alpha ,\; \beta ,\;\gamma \right)\), we have conducted a brief simulation study based on values of the following sets of parameters.

  1. (i)

    \(\alpha =1.335 ,\; \beta =0.399,\; \gamma =2.668,\;\mu =0.489,\; \sigma = 0.575\) (negatively skewed).

  2. (ii)

    \(\alpha =5.335 ,\; \beta =0.400,\; \gamma =0.668,\; \mu =0.490,\; \sigma = 0.576\) (positively skewed).

Here we adopt the inverse transform method of Ross [15] for generating random numbers. The computed values of bias and mean square errors (MSE) corresponding to sample sizes 30, 100, 200 , 300 and 500 respectively are given in Table  3. From Table  3 it can be seen that both the absolute bias and MSEs in respect of each parameters of the EGGLD are in decreasing order as the sample size increases.

Table 1 Estimated values of the parameters with the corresponding \(KSS,\; AIC,\; BIC,\; CAIC\; \text {and}\; HQIC\) values
Full size table
Table 2 Calculated value of the test statistic
Full size table
Table 3 Bias and mean square error (MSE) within brackets of the simulated data sets
Full size table
Fig. 1
figure 1

Plots of PDF of the GGLD for varying values of \(\alpha\) and \(\beta\) and \(\gamma\)

Full size image
Fig. 2
figure 2

Hazard rate function of GGLD for varying values of \(\alpha\) and \(\beta\) and \(\gamma\)

Full size image
Fig. 3
figure 3

Empirical distribution of the data set1 along with the fitted CDFs

Full size image
Fig. 4
figure 4

Empirical distribution of the data set2 along with the fitted CDFs

Full size image

7 Discussion

While considering practical applications, most of the real life data sets are not symmetric in nature. So, in the present work we developed certain wide classes of asymmetric logistic distributions through the names “generalized gamma logistic distribution (GGLD)” and “extended generalized gamma logistic distribution (EGGLD)”. The EGGLD has been fitted to two medical data sets and shown that the EGGLD gives best fit to both the data sets compared to the existing models such as LD, LDI and LDII, DLD based on various measures such as the KSS, AIC, BIC, CAIC and HQIC values. Figures  3 and 4 also supports in favour to the EGGLD as the best model.

8 Conclusion

In this paper, we have developed a wide class of generalised logistic distribution GGLD, which will be suitable for asymmetric data sets compared to the existing models. This model is a generalized class of both the LDI and LDII models. Some of the important characteristics of the distribution have been discussed via deriving mean, variance, characteristic function, measures of skewness and kurtosis, entropy etc. along with the distribution of its order statistics and maximum likelihood estimation of its parameters. Two real life medical data sets are utilized for illustrating the usefulness of the model and a simulation study is conducted for examining the performance of the maximum likelihood estimators of the parameters of the distribution. Several inferential aspects as well as structural properties of the model are yet to study.