On Some Mixing Properties of Copula-Based Markov Chains

Abstract

This paper brings some insights of $\psi '$-mixing, $\psi ^*$-mixing and $\psi$-mixing for copula-based Markov chains and the perturbations of their copulas. We provide new tools to check Markov chains for $\psi$-mixing or $\psi '$-mixing. We show that perturbations of $\psi '$-mixing copula-based Markov chains are $\psi '$-mixing while perturbations of $\psi$-mixing Markov chains are not necessarily $\psi$-mixing Markov chains, even when the perturbed copula generates $\psi$-mixing. The Farlie–Gumbel–Morgenstern, gaussian and Ali-Mikhail-Haq copula families are considered among other examples. A statistical study is provided to emphasize the impact of perturbations on copula-based Markov chains in a simulation study. Moreover, we provide a correction to a statement made in Longla et al. (J Korean Stat Soc, 1–23, 2021) on $\psi$-mixing.

1 Introduction

Modelling dependence among variables or factors in economics, finance, risk management and other applied fields has benefited over the last decades from the study of copulas. For recent applications of copulas, see [14, 28]. More references of such applications can be found in the review paper of Bhati and Do [2]. Copulas, these multivariate cumulative distributions with uniform marginals on the interval [0, 1], have been widely used as strength of dependence between variables. Sklar [27] first showed that by rescaling the effect of marginal distributions, one obtains a copula from the joint distribution of random variables. This rescaling implies that when variables are transformed using increasing functions, the copula of their transformations remains same as that of the original variables. For many dependence coefficients, this copula is all that affects the computations (random vectors with common copulas have common dependence coefficients). This justifies why dealing with the uniform distribution as stationary distribution of a Markov chain is same as studying a Markov chain with any absolutely continuous stationary distribution. Following the ideas of Durante et al. [8], Longla et al. [15] and Longla et al. [16] have considered the perturbation method that adds to a copula an extra term called perturbation. They also considered other classes of modifications and their impact on the dependence structure as studied by Komornik et al. [13]. The long run impact of such perturbations on the dependence structure and the measures of association was investigated. In fact, they investigated the impact of perturbations of copulas on the mixing structure of the Markov chains that they generate. The case was presented for $\rho$-mixing, $\alpha$-mixing, $\psi$-mixing and $\beta$-mixing in Longla et al. [15] and [16]. Our work concerns the case of $\psi$-mixing, $\psi '$-mixing and $\psi ^*$-mixing.

1.1 Facts About Copulas

The definition of a 2-copula and related topics can be found in Nelsen [24]. 2-copulas are in general referred to as copulas when there is no reason for confusion. We will follow this assumption throughout this paper. A function $C: [0,1]^{2}\rightarrow [0,1]$ is called a bivariate copula if it satisfies the following conditions:

• i. $C(0,x)=C(x,0)=0$ (meaning that C is grounded);

• ii. $C(x,1)=C(1,x)=x, \forall x\in [0,1]$ (meaning that each coordinate is uniform on [0,1]);

• iii. $C(a,c)+C(b,d)-C(a,d)-C(b,c)\ge 0, \forall \ {}[a,b]\times [c,d]\subset [0,1]^{2}.$

The last condition basically states that the probability of any rectangular subset of $[0,1]\times [0,1]$ is non-negative. This is an obvious condition, given that C(x, y) is a cumulative probability distribution function on $[0,1]\times [0,1]$. The first condition states that the probability of any rectangle that doesn’t intersect $[0,1]\times [0,1]$ is equal to 0 (this is because such a rectangle doesn’t intersect the support of the distribution function that has cumulative distribution C(u, v)). The second condition confirms that the marginal distribution is uniform on [0, 1] for each of the components of the considered vector.

Darsaw et al. [7] derived the transition probabilities for stationary Markov chains with uniform marginals on [0, 1] as $P(X_{n}\in (-\infty ,x]|X_{n-1}=x)=C_{,1}(x,y), \forall n\in {\mathbb {N}}$, where $C_{,i}(x,y)$ denotes the derivative of C(x, y) with respect to the $i\mathrm{th}$ variable. This property has been used by many authors to establish mixing properties of copula-based Markov chains. We can cite [18, 19, 21] who provided some results for reversible Markov chains, Beare [1] who presented results for $\rho$-mixing among others.

It’s been shown in the literature (see [7] and the references therein) that if $(X_1, \ldots , X_n)$ is a Markov chain with consecutive copulas $(C_1, \ldots , C_{n-1})$, then the fold product given by

$$\begin{aligned} C(x,y)=C_1*C_2 (x, y)=\int ^1_0 C_{1,2}(x, t)C_{2,1}(t, y)dt \end{aligned}$$

is the copula of $(X_1,X_3)$ and the $\star$-product given by

$$\begin{aligned} C(x,y,z)=C_1\star C_2 (x, y,z)=\int _0^y C_{1,2}(x, t)C_{2,1}(t, z)dt \end{aligned}$$

is the copula of $(X_1,X_2,X_3)$. The n-fold product of C(x, y) denoted $C^n(x,y)$ is defined by the recurrence $C^{1}(x,y)=C(x,y)$,

$$\begin{aligned} C^{n}(x,y)=C^{n-1}*C(x,y). \end{aligned}$$

Some of the most popular copulas are $\Pi (u,v)=uv$ (the independence copula), the Hoeffding lower and upper bounds $W(u,v)=\max (u+v-1,0)$ and $M(u,v)=\min (u,v)$ respectively. Convex combinations of copulas $\{C_1(x,y), \ldots , C_k(x,y)\}$ defined by $\{ C(x,y)=\sum _{j=1}^{k}a_j C_j(x,y), 0\le a_j, \sum _{j=1}^{k} a_j=1\}$ are copulas. For any copula C(x, y), there exists a unique representation $C(x, y) = AC(x, y) + SC(x, y)$, where AC(x, y) is the absolute continuous part of C(x, y) and SC(x, y) is the singular part of the copula C(x, y). AC(x, y) induces on $[0,1]^2$ a measure $P_c$ defined on borel sets by

$$\begin{aligned}\displaystyle P_c(A\times B)&=\int _A\int _B c(x,y)dxdy\quad \text {and} \quad P(A\cap B)\\& =P_c(A\times B)+SC(A\times B), \quad \text {(see Longla (2015)).} \end{aligned}$$

An absolutely continuous copula is one that has singular part $SC(x,y)=0$ and a singular copula is one that has absolutely continuous part $AC(x,y)=0$. This work is concerned mostly by absolutely continuous copulas and mixing properties of the Markov chains they generate.

1.2 Mixing Coefficients of Interest

The mixing coefficients of interest in this paper are $\psi '$ and $\psi$. The $\psi$-mixing condition has its origin in the paper by Blum et al. [3]. They studied a different condition (“$\psi$*-mixing”) similar to this mixing coefficient. They showed that for Markov chains satisfying their condition, the mixing rate is exponential. The coefficient took its present form in the paper of Philipp [25]. For examples of mixing sequences, see [10], who showed that in general, the mixing rate could be arbitrarily slow, a large class of mixing rates can occur for stationary $\psi$-mixing. It’s been shown that $\psi ^*$-mixing is equivalent to $\psi$-mixing for Markov chains (see page 206 of Bradley [4]). General definitions of these mixing coefficients are as follows. Given any $\sigma$-fields ${\mathscr {A}}$ and ${\mathscr {B}}$ and a defined probability measure P,

$$\begin{aligned} \psi ({\mathscr {A}},{\mathscr {B}})= & {} \sup _{B\in {\mathscr {B}}, A\in {\mathscr {A}}, P(A)\cdot P(B)>0 }\frac{|P(A\cap B)-P(A)P(B)|}{P(A)P(B)}, \\ \psi '({\mathscr {A}},{\mathscr {B}})= & {} \inf _{B\in {\mathscr {B}}, A\in {\mathscr {A}}, P(A)>0}\frac{P(B\cap A)}{P(A)P(B)}, \quad \\ \text {and}\quad \psi ^*({\mathscr {A}},{\mathscr {B}})= & {} \sup _{B\in {\mathscr {B}}, A\in {\mathscr {A}}, P(A)\cdot P(B)>0 }\frac{P(A\cap B)}{P(A)P(B)}. \end{aligned}$$

In case of stationary copula-based Markov chains generated by an absolutely continuous copula and the uniform distribution of the interval [0, 1], the $\psi '$-mixing dependence coefficient takes the form

$\psi '_n(C)=\underset{\underset{ \lambda (A)\lambda (B)>0}{ A,B\in {\mathscr {B}}}}{\inf }\dfrac{\int _A\int _B c_n(x,y)dxdy}{\lambda (A)\lambda (B)},$

where $c_n(x,y)$ is the density of the of $C^n(x,y)$ and $\lambda$ is the Lebesgue measure on $I=[0,1]$. For every positive integer n, let $\mu _n$ be the measure induced by the distribution of $(X_0, X_n)$. Let $\mu$ be the measure induced by the stationary distribution of the Markov chain and ${\mathscr {B}}$ the $\sigma$-algebra generated by $X_0$. The $\psi '$-mixing dependence coefficient takes the form

$$\begin{aligned} \psi _n'(C)= & {} \underset{A,B\in {\mathscr {B}}, \mu (A).\mu (B)>0~}{\inf }\dfrac{\mu _n(A\times B)}{\mu (A)\mu (B)},\\ \quad \hbox { and }\quad \psi _n^*(C)= & {} \underset{A,B\in {\mathscr {B}}, \mu (A).\mu (B)>0~}{\sup }\dfrac{\mu _n(A\times B)}{\mu (A)\mu (B)}. \end{aligned}$$

For more on the topic, see [1, 12, 20].

1.3 About Perturbations

In applications, knowing approximately a copula C(u, v) appropriate to the model of the observed data, minor perturbations of C(u, v) are considered. Komornik et al. [13] have investigated some perturbations that were introduced by Mesiar et al. [23]. These perturbations were also considered by Longla et al. [15] and [16]. Perturbations that we consider in this work have been studied by many authors. Sheikhi et al. [26] looked at the perturbations of copulas via modification of the random variables that the copulas represent. They perturbed the copula of (X, Y) by looking at the copula of $(X+Z, Y+Z)$ for some Z independent of (X, Y) that can be considered as noise. Mesiar and al. [22] worked on the perturbations induced by modification of one of the random variables of the pair. Namely, the copula of (X, Y) was perturbed to obtain the copula of $(X+Z, Y)$. In this work, we look at the impact of perturbations on $\psi$-mixing and $\psi '$-mixing. We provide theoretical proofs and a simulation study that justifies the importance of the study of perturbations and their impact on estimation problems. This is done through the central limit theorem that varies from one kind of mixing structure to another and is severely impacted by perturbations, for instance, in the case of $\psi$-mixing.

1.4 Structure of the Paper

This paper consists of six sections, each of which concern a specific topic of interest and is structured as follows. Introduction in Sect. 1 is divided into several parts. Facts about copulas are introduced in Sect. 1.1, mixing coefficient of interest ($\psi '$-mixing and $\psi$-mixing) are defined in Sects. 1.2 and 1.3 is dedicated to facts about perturbation of copulas. Section 2 is devoted to the impact of perturbations on $\psi '$-mixing, $\psi ^*$-mixing and $\psi$-mixing copula-based Markov chains, addressing $\psi '$-mixing in Sect. 2.1 and $\psi$-mixing in Sect. 2.2. We emphasize the fact that perturbations of $\psi '$-mixing copula-based Markov chains are $\psi '$-mixing while perturbations of $\psi$-mixing Markov chains are not necessarily $\psi$-mixing. We present the case of $\psi ^*$-mixing. This section ends by an example. In Sect. 3 we provide some graphs to show the effect of perturbations. In Sect. 4, we showcase a simulation study to emphasize the importance of this topic. Comments on the paper’s results and their relationship with current state of art are presented in Sects. 5 and 6 provides proofs of our main results. Throughout this work $\psi _n(C)$ is replaced by $\psi _n$ when there is no reason for confusion.

2 Facts About $\psi '$-Mixing, $\psi ^*$-Mixing and $\psi$-Mixing

It is important to recall that we are only interested by the case of Markov chains. In this set up, the Markov chain property simplifies the formulas of mixing coefficients of interest and properties of the copula can be enough to identify the mixing structure of the sequence of associated random variables.

2.1 All About $\psi '$-Mixing

Longla [18] showed that for a copula with density of absolutely continuous part bounded away from 0, Markov chains it generates are $\psi '$-mixing. This result was extended to convex combinations of copulas by Longla et al. [16] using the result of Bradley [6] that states that for any strictly stationary Markov chain, either $\psi '_n\rightarrow 1$ as $n\rightarrow \infty$ or $\psi '_n=0$ $\forall n\in {\mathbb {N}}$. Based on this result, we show the following for stationary Markov chains with marginal distribution uniform on the interval [0, 1].

Theorem 2.1.1

Let $\lambda$ be the Lebesgue measure on [0, 1]. If the copula C(u, v) of the stationary Markov chain $(X_k, k\in {\mathbb {N}})$ is such that the density of its absolutely continuous part $c(u,v)\ge \varepsilon _1(u)+\varepsilon _2(v)$ on a set of Lebesgue measure 1 and $\displaystyle \inf _{A\subset I}\frac{\int _{A}\varepsilon _1d\lambda }{\lambda (A)}>0$ or $\displaystyle \inf _{A\subset I}\frac{\int _{A}\varepsilon _2 d\lambda }{\lambda (A)}>0$, then the Markov chain is $\psi '$-mixing.

Theorem 2.1.1 is an extension of Theorem 2.5 of Longla [19]. It extends the result from $\rho$-mixing to $\psi '$-mixing. Longla et al. [15] state that for a copula C perturbed by means of the independence copula $\Pi$, the following result holds for the perturbation copula $C_{\theta ,\Pi }(u,v)$ with parameter $\theta$.

$$\begin{aligned} C_{\theta ,\Pi }^{n}(u,v)=(1-\theta )^nC^{n}(u,v)+(1-(1-\theta )^n)uv. \end{aligned}$$

(1)

As a result of this formula, following [18], based on the fact that the density of the copula $C_{\theta ,\Pi }^{n}(u,v)$ is bounded away from zero on a set of Lebesgue Measure 1, we conclude the following.

Corollary 2.1.2

For any copula C(u, v), the perturbation copula $C_{\theta ,\Pi }(u,v)$ generates $\psi '$-mixing stationary Markov chains with the uniform distribution on the interval [0, 1] as stationary distribution.

In general, for any convex combination of copulas, the following result holds.

Theorem 2.1.3

For any set of copulas $C_1(u,v)\ldots C_k (u,v)$, if there exists a subset of copulas $C_{k_1}\ldots C_{k_s},$ $s\le k\in {\mathbb {N}}$ such that $\psi '({\hat{C}})>0 \quad \text {for}\quad {\hat{C}}=C_{k_1}*\cdots *C_{k_s},$ then $\psi '_{s}(C)>0$ and any Markov chain generated by

$$\begin{aligned}&C=a_1C_1+\cdots +a_k C_k,\quad \text {for } \quad 0<a_1,\ldots ,a_k<1, \\& \sum _{i=1}^k a_i =1, \quad \text {is exponential}\quad \psi '\text {-mixing}. \end{aligned}$$

Theorem 2.1.4

For any set of copulas $C_1(u,v)\ldots C_k (u,v)$, if there exists a subset of copulas $C_{k_1}\ldots C_{k_s},$ $s\le k\in {\mathbb {N}}$ such that the density of the absolutely continuous part of ${\hat{C}}(u,v)$ is bounded away from 0 $\text {for}\quad {\hat{C}}=C_{k_1}*\cdots *C_{k_s},$ then $\psi '_{s}(C)>0$ and any Markov chain generated by

$$\begin{aligned}&C=a_1C_1+\cdots +a_k C_k,\quad \text {for } \quad 0<a_1,\dots ,a_k<1, \\& \sum _{i=1}^k a_i =1, \quad \text {is exponential}\quad \psi '\text {-mixing}. \end{aligned}$$

2.2 All About $\psi$-Mixing and $\psi ^*$-Mixing

It’s been shown in the literature that $\psi$-mixing implies $\psi '$-mixing, $\psi ^*$-mixing and other mixing conditions. See for instance [4]. We emphasize here that the above theorems cannot be extended to $\psi$-mixing in general by exhibiting cases when the conditions of the theorems are satisfied, but there is no $\psi$-mixing. It’s good to recall that for markov chains, $\psi ^*$-mixing is equivalent to $\psi$-mixing. So, any result stated in this paper for $\psi ^*$-mixing is valid for $\psi$-mixing. A result of Bradley [6] states that for a strictly stationary mixing sequence, either $\psi ^*_n=\infty$ for all n or $\psi ^*_n\rightarrow 1$ as $n\rightarrow \infty$.

Based on this result, if we want to show that a stationary Markov chain is $\psi ^*$-mixing, it is enough to show that it is mixing and $\psi ^*_1\ne \infty$. It needs to be clear that this is not a necessary condition. In fact, there is $\psi ^*$-mixing for any mixing sequence whenever we can show that for some positive integer n, $\psi ^*_n\ne \infty$. The required mixing condition is implied by any of the mixing properties defined in this paper. It is mixing in the ergodic theoretic sense, that we do not define in this paper. References to this mixing can be found in Bradley [4]. A remark of Longla et al. [15] states the following.

Remark 2.2.1

In general, for any convex combination of two copulas (here $0 \le a \le 1)$, the $\psi$-mixing coefficient satisfies the following inequalities:

$$\begin{aligned} \psi (aC_1 + (1-a)C_2)\le & \,{} a\psi (C_1) + (1-a) \psi (C_2); \end{aligned}$$

(2)

$$\begin{aligned} \psi (aC_1 + (1-a)C_2)\ge &\, {} a\psi (C_1) -(1-a) \psi (C_2).\end{aligned}$$

(3)

A result of Longla et al. [15] states that a convex combination of copulas generates stationary $\psi$-mixing Markov chains if each of the copulas of the combination generates $\psi$-mixing stationary Markov chains. This statement was not fully proven and might not be true as stated. Based on the provided proof, the correct statement should be as follows.

Theorem 2.2.2

A convex combination of copulas generates stationary $\psi$-mixing Markov chains if each of the copulas of the combination generates $\psi$-mixing stationary Markov chains with $\psi _1< 1$.

We now state the following result for $\psi ^*$-mixing that is also true for $\psi$-mixing in the case of Markov chains.

Theorem 2.2.3

Assume that $(X_i, 1\le i\le n)$ is a stationary Markov chain generated by the absolutely continuous copula C(u, v) and the continuous marginal distribution F. The following holds.

• 1. If for some positive integer n, the density of $C^n(u,v)$ is bounded above on $[0,1]^2$ and for some s the density of $C^s(u,v)$ is bounded away from 0, then Markov chain is $\psi$-mixing.

• 2. If for some n, $c^n(u,v)\le m<2$ on $[0,1]^2$, where $c^n(u,v)$ is the density of $C^n(u,v)$ and m is a constant, then the Markov chain is $\psi$-mixing.

• 3. If for every n the density of $C^n(u,v)$ is continuous and not bounded above on $[0,1]^2$, then the Markov chain is not $\psi ^*$-mixing.

2.2.1 Examples

We consider two classes of copulas that are widely used in the literature: The gaussian copula and the Ali-Mikhail-Haq copula families.

• 1. The bivariate gaussian copula and the Markov chains it generates. The bivariate gaussian copula $C_\rho (u,v)$ is obtained from the joint gaussian distribution of $(X_1,X_2)$ via Sklar’s theorem (see [24]). Assuming that $X_1$ and $X_2$ follow the standard normal distribution, the covariance matrix has the form

  $$\begin{aligned} R={1 \quad \rho \atopwithdelims ()\rho \quad 1}, \quad \text {where }\rho \text { is the covariance of the variables }X_1\text { and }X_2. \end{aligned}$$

  Therefore, the density of the bivariate gaussian copula is defined as

  $$\begin{aligned} \frac{1}{\sqrt{|R|}}e^{-\frac{1}{2}(\Phi ^{-1}(u)_{} \quad {}_{} \Phi ^{-1}(v))(R^{-1}-{\mathbb {I}}){\Phi ^{-1}(u)\atopwithdelims ()\Phi ^{-1}(v)}}, \end{aligned}$$

  where ${\mathbb {I}}$ is the $2\times 2$ identity matrix and $\Phi ^{-1}(x)$ is the quantile function of the standard normal distribution. Via simple computations, it is established that

  $$\begin{aligned} c_{\rho }(u,v)=\frac{1}{\sqrt{1-\rho ^2}}e^{-\frac{\rho ^2}{2(1-\rho ^2)}([\Phi ^{-1}(u)]^2-\frac{2}{\rho }\Phi ^{-1}(u)\Phi ^{-1}(v)+[\Phi ^{-1}(v)]^2)}. \end{aligned}$$

  This density is equal to 1 when $\rho =0$ because in this case the two random variables are independent and their copula is the product copula. It is also obvious the $\rho =1$ and $\rho =-1$ are excluded because in these two cases, the original variables are linearly dependent and either have copula M(u, v) when $\rho =1$ or W(u, v) when $\rho =-1$.

        It is clear that when $\rho \ne 0$, this density is not bounded above because for $u=\Phi (\frac{1}{\rho }\Phi ^{-1}(v))$, we have

  $$\begin{aligned} f(v):=c_{\rho }(u,v)=\frac{1}{\sqrt{1-\rho ^2}}e^{\frac{1}{2}[\Phi ^{-1}(v)]^2}, \end{aligned}$$

  and as $v\rightarrow 1$, we have $f(v)\rightarrow \infty$ for any $\rho \ne 0$. Therefore, by simple computations, we have that any bivariate gaussian copula that is not the independence copula has a density that is not bounded above. Based on the $*$-product of copulas, we show next that for any stationary Markov chain based on gaussian copulas, the copula of any pair of variables of the chain is gaussian. Moreover, the $*$-product of two gaussian copulas is the independence copula if and only if one of them is the independence copula.

Proposition 2.2.4

For any gaussian copulas $C_{\rho _1}(u,v)$ and $C_{\rho _2}(u,v)$, the following holds.

• (a) $C_{\rho _1}*C_{\rho _2}(u,v)=C_{\rho _1\rho _2}(u,v)$,

• (b) $C^n_{\rho _1}(u,v)=C_{\rho ^n_1}(u,v)$.

It is enough to show that $C_{\rho _1}*C_{\rho _2}(u,v)=C_{\rho _1\rho _2}(u,v)$, wich is equivalent to showing that

$$\begin{aligned} \int _0^1c_{\rho _1}(u,t)c_{\rho _2}(t,v)dt=c_{\rho _1\rho _2}(u,v). \end{aligned}$$

This equality holds because

$$\begin{aligned}&\displaystyle \int _0^1 c_{\rho _1}(u,t)c_{\rho _2}(t,v)dt=\frac{1}{\sqrt{(1-\rho _1^2)(1-\rho _2^2)}} \\&\quad \times \int _0^1e^{-\frac{\rho _1^2}{2(1-\rho _1^2)}([\Phi ^{-1}(u)]^2-\frac{2}{\rho _1}\Phi ^{-1}(u)\Phi ^{-1}(t)+[\Phi ^{-1}(t)]^2)-\frac{\rho _2^2}{2(1-\rho _2^2)}([\Phi ^{-1}(t)]^2-\frac{2}{\rho _2}\Phi ^{-1}(t)\Phi ^{-1}(v)+[\Phi ^{-1}(v)]^2)}dt. \end{aligned}$$

If we denote $s=\Phi ^{-1}(u)$, $r=\Phi ^{-1}(v)$ and $z=\Phi ^{-1}(t)$, then $t=\Phi (z)$ and $dt=\frac{1}{\sqrt{2\pi }}e^{-z^2/2}dz$. Therefore,

$$\begin{aligned} A= & {} \frac{1}{\sqrt{(1-\rho _1^2)(1-\rho _2^2)}}\int _{-\infty }^{\infty }\frac{1}{\sqrt{2\pi }}e^{-\frac{\rho _1^2}{2(1-\rho _1^2)}(s^2-\frac{2}{\rho _1}sz+z^2)-\frac{\rho _2^2}{2(1-\rho _2^2)}(z^2-\frac{2}{\rho _2}zr+r^2)-\frac{1}{2}z^2}dz\\= & {} \frac{(\sqrt{2\pi })^{-1}}{\sqrt{(1-\rho _1^2)(1-\rho _2^2)}}\int _{-\infty }^{\infty }e^{\frac{-(1-\rho _1^2\rho _2^2)}{2(1-\rho _1^2)(1-\rho _2^2)}[(z-\frac{s\rho _1(1-\rho ^2_2)+r\rho _2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2})^2 -(\frac{s\rho _1(1-\rho ^2_2)+r\rho _2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2})^2+\frac{s^2\rho _1^2(1-\rho ^2_2)+r^2\rho _2^2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2}]}dz \end{aligned}$$

The quatratic portion in z is identified to the Normal distribution with variance

$\displaystyle \frac{(1-\rho _1^2)(1-\rho _2^2)}{1-\rho _1^2\rho _2^2}$ and mean $\displaystyle \frac{s\rho _1(1-\rho ^2_2)+r\rho _2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2}$. This leads to

$$\begin{aligned} A= \frac{\sqrt{(1-\rho _1^2)(1-\rho _2^2)}}{\sqrt{(1-\rho _1^2\rho _2^2)}\sqrt{(1-\rho _1^2)(1-\rho _2^2)}} e^{\frac{-(1-\rho _1^2\rho _2^2)}{2(1-\rho _1^2)(1-\rho _2^2)}\left[ -\left( \frac{s\rho _1(1-\rho ^2_2)+r\rho _2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2}\right) ^2+\frac{s^2\rho _1^2(1-\rho ^2_2)+r^2\rho _2^2(1-\rho ^2_1)}{1-\rho _1^2\rho _2^2}\right] }. \end{aligned}$$

The last equality simplifies to

$$\begin{aligned} A= \frac{1}{\sqrt{1-\rho _1^2\rho _2^2}} e^{\frac{-\rho _1^2\rho _2^2}{2(1-\rho _1^2\rho _2^2)}\left[ s^2-\frac{1}{1-\rho _1\rho _2}sr+r^2\right] }=c_{\rho _1\rho _2}(u,v). \end{aligned}$$

This ends the proof of Proposition 6.2.1. In Beare [1] it was reported that gaussian copulas have square integrable densities with $L_2$-norm $\frac{1}{\sqrt{1-\rho ^2}}$. We have just shown that the density of the fold-product of $C_{\rho }(u,v)$ is not continuous on $(0,1)^2$ and not bounded on $[0,1]^{2}$. Therefore, Theorem 2.2.3 implies the following.

Corollary 2.2.5

Any Copula-based Markov chain generated by a gaussian copula that is not the product copula is not $\psi$-mixing.

The proof of Corollary 2.2.5 is an application of Theorem 2.2.3 and the fact that the copula of $(X_0,X_n)$ is $C_{\rho ^n}(u,v)$; and $c_{\rho ^n}(u,v)$ is not bounded as shown above for any value of the correlation $\rho ^n$ or for any n.

• 2. The Ali-Mikhail-Haq copula and the Markov chains they generate.

  Copulas from the Ali-Mikhail-Haq family are defined for $\theta \in [-1,1]$ by

  $$\begin{aligned}&C_\theta (u,v)=\frac{uv}{1-\theta (1-u)(1-v)} \quad \text {with density}\quad \\&c_\theta (u,v)=\frac{(1-\theta )(1-\theta (1-u)(1-v))+2\theta uv}{(1-\theta (1-u)(1-v))^3}. \end{aligned}$$

  It is easy to see that this density is continuous and satisfies $(1-\theta )^2\le c_{\theta }(u,v)\le \frac{1+\theta }{(1-\theta )^3}$ when $1>\theta \ge 0$ or $\frac{1+\theta }{(1-\theta )^3}\le c_{\theta }(u,v)\le (1-\theta )^2<2$ when $-1<\theta \le 0$. From these inequalities, it follows that when $-1< \theta <1$, the density is bounded away from 0. Therefore, the copula generates $\psi '$-mixing. $\psi '$-mixing implies mixing. Therefore, due to the upper bound on the density, Theorem 2.2.3 implies the following.

Corollary 2.2.6

Any copula from the Ali-Mikhail-Haq family of copulas with $|\theta |\ne 1$ generates $\psi ^*$-mixing stationary Markov chains.

• 3. Copulas with densities $m_1, m_2, m_3$ and $m_4$ of Longla [19] and the Markov chains they generate.

  Each of these copulas is bounded when the functions g(x) and h(x) used in their definitions are bounded. It was shown in Longla [19] that each of these copulas generates $\rho$-mixing. $\rho$-mixing implies mixing. Therefore, Thoerem 2.2.3 implies the following.

Corollary 2.2.7

All copulas with densities $m_1, m_2, m_3$ and $m_4$ of Longla [19] with bounded functions g(x) and h(x) generate $\psi$-mixing Markov chains.

2.2.2 The Farlie–Gumbel–Morgenstern Copula Family

This family of copulas is defined by $C_{\theta }(u,v)=uv+\theta uv(1-u)(1-v)$, for $\theta \in [-1,1]$. Longla [19] showed that these copulas generate geometrically ergodic Markov chains. Moreover, due to symmetry, the Markov chains they generate are also reversible. Therefore, geometric ergodicity implies exponential $\rho$-mixing. Longla [18] showed that These copulas generate $\psi '$-mixing when $|\theta |<1$. We will improve this result in this section by showing that for all values of the parameter, these copulas generate $\psi$-mixing.

Theorem 2.2.8

For any member of the Farlie–Gumbel–Morgenstern family of copula with parameter $\theta$, the joint distribution of $(X_0,X_n)$ for a stationary copula-based Markov chain generated is

$$\begin{aligned} C_{\theta }^n(u,v)=uv+3\left( \frac{\theta }{3}\right) ^n uv(1-u)(1-v). \end{aligned}$$

(4)

The density of this copula is $c^n_{\theta }(u,v)=1+3(\frac{\theta }{3})^n(1-2u)(1-2v)$. Via simple calculations, it follows that

$$\begin{aligned} 0\le 1-3\left( \frac{|\theta |}{3}\right) ^n\le c^n_{\theta }(u,v)\le 1+3\left( \frac{|\theta |}{3}\right) ^n. \end{aligned}$$

(5)

These inequalities are used to establish the following result.

Theorem 2.2.9

Any Copula-based Markov chain generated by a copula from the Farlie–Gumbel–Morgenstern family is $\psi$-mixing for any $\theta \in [-1,1]$.

It has been established, using the first inequality of (5) when $n=1$ and a weaker form of Theorem 2.1.4, that any copula from this family with $|\theta |\ne 1$ generates exponential $\psi '$-mixing. We now show via integration that for any copula-based Markov chain $(X_1,\ldots , X_n)$ generated by $C_{\theta }(u,v)$, if $A\in \sigma (X_1)$ and $B\in \sigma (X_{n+1})$, then

$$\begin{aligned} 1-3\left( \frac{|\theta |}{3}\right) ^n \le \frac{P^n(A\cap B)}{P(A)P(B)}\le 1+3\left( \frac{|\theta |}{3}\right) ^n. \end{aligned}$$

(6)

Formula (6) implies that $\displaystyle \sup _{A,B}\frac{P^n(A\cap B)}{P(A)P(B)}\le 1+3(\frac{|\theta |}{3})^n<2$, for $n> 1$ and $|\theta |\le 1$. It follows from Theorem 3.3 of Bradley [5] that this Markov chain is exponential $\psi$-mixing for all values of $\theta$.

2.2.3 The Mardia and Frechet Families of Copula

Any copula from the Mardia family is represented as $\displaystyle C_{\alpha , \beta }(u,v)=\alpha M(u,v)+\beta W(u,v)+ (1-\alpha -\beta )\Pi (u,v),$ with $0\le \alpha , \beta , 1-\alpha -\beta \le 1$. The Frechet family of copulas is a subclass of the Mardia family with $\alpha +\beta =\theta ^2$. The two families enjoy the same mixing properties and their analysis is theoretically identical. The density of any copula of these families is bounded away from zero on a set of Lebesgue measure 1. Therefore, the results of this paper imply that these families generate $\psi '$-mixing. Now, consider $(X_1,X_2)$ with joint distribution $C_{\alpha ,\beta }(u,v)$ and the sets $A=(0,\varepsilon )$ and $B=(1-\varepsilon , 1)$. Via simple calculations, we obtain

$$\begin{aligned} P(A\cap B)=(1-\alpha -\beta )\varepsilon ^2+\beta \varepsilon . \end{aligned}$$

(7)

Thus,

$$\begin{aligned} \sup _{A,B}\frac{P(A\cap B)-P(A)P(B)}{P(A)P(B)}\ge sup_{\varepsilon }\left( -\alpha -\beta +\frac{\beta }{\varepsilon }\right) =\infty . \end{aligned}$$

(8)

To complete the proof, we use the fact that based on the result of Longla [19], the joint distribution of $(X_1, X_{n+1})$ is $C^n(u,v)$-member of the Mardia family of copulas. This fact and formula (8) imply that $\psi _n=\infty$ for all n. Therefore, this copula doesn’t generate $\psi$-mixing as a result of Bradley [6]. Hence, the results of this work cannot be extended to $\psi$-mixing for copulas with non-zero singular parts. One of the issues is that in this case, $\lambda =1$ ceases to be eigen function of the density of the absolutely continuous part of the copula. The idea of this proof leads to the following.

Theorem 2.2.10

Let C(u, v) be a copula that generates non $\psi ^*$-mixing stationary Markov chains with $\psi ^*_n=0$ for all n. Any convex combination of copulas containing C(u, v) generates non $\psi ^*$-mixing stationary Markov chains.

Theorem 2.2.10 combined with Longla et al. [16] imply the following result.

Theorem 2.2.11

A convex combination of copulas generates $\psi ^*$-mixing stationary Markov chains if every copula it contains generates $\psi ^*$-mixing stationary Markov chains with $\psi ^*_1<2$.

2.2.4 General Case of Lack of $\psi$-Mixing in Presence of $\psi '$-Mixing

Here we present a large class of copulas that generate $\psi '$-mixing Markov chains, but don’t generate $\psi$-mixing Markov chains. Based on the results of this paper, the following general corollary holds.

Corollary 2.2.12

Any convex combination of copulas that contains the independence copula $\Pi (u,v)$ and M(u, v) or W(u, v) generates exponential $\psi '$-mixing stationary Markov chains, but doesn’t generate $\psi$-mixing stationary Markov chains.

This is a consequence of Theorem 2.2.10 and Longla [18]. Because the convex combination contains $\Pi (u,v)$, the density of its absolutely continous part is bounded away from 0 on $[0,1]^2$. Therefore, by Longla [18], it generates $\psi '$-mixing stationary Markov chains. Because the combination contains M(u, v) or W(u, v), for which $\psi _n=\infty$ for all n, by Theorem 2.2.10, it doesn’t generate $\psi$-mixing stationary Markov chains.

3 Some Graphs of Copulas and Their Perturbations

Here, we provide graphical representations of the impact of perturbations of copulas on Markov chains generated by them. The case is presented for some examples from the Frechet and Farlie–Gumbel–Morgenstern families of copulas. Examples are chosen for values of parameters that are close to independence and the extreme case of each of the families. Two graphs of data on $(0,1)^2$ are provided as well as two graphs for the standard normal distribution as marginal distribution of the Markov chains. To generate a Markov chain with a copula from the Farlie–Gumbel–Morgenstern family, we proceed as follows.

• (a) Generate $U_1$ from Uniform(0, 1);

• (b) For $t=2,\ldots n,$ generate $W_t$ from Uniform(0, 1) and solve for $U_t$ the equation $W_t= U_t+\theta (1-2U_{t-1})U_t(1-U_{t})$;

• (c) Set $Y_t=G^{-1}(U_t)$, where G(t) is the common marginal distribution of the variables of the stationary Markov chain.

Longla et al. [15] worked on perturbation of copulas and their properties. For a copula C(u, v), some of the studied perturbations are as follows. Assume $\alpha \in [0,1]$.

$$\begin{aligned} {\tilde{C}}_{\alpha }(u,v)= & \, {} C(u,v)+\alpha \left( \Pi (u,v)-C(u,v)\right) , \end{aligned}$$

(9)

$$\begin{aligned} {\hat{C}}_{\alpha }(u,v)= & \, {} C(u,v)+\alpha \left( \text {M}(u,v)-C(u,v)\right) . \end{aligned}$$

(10)

Formulas (9) and (10) lead to the following.

Proposition 3.0.1

Let $\alpha \in [0,1]$, $\theta \in [-1,1]$ and $C_{\theta }(u,v)$ be a Farlie–Gumbel–Morgenstern copula.

$$\begin{aligned} {\tilde{C}}_{\alpha ,\theta }(u,v)= & \, {} C_{\theta }(u,v)+\alpha \left( \Pi (u,v)-C_{\theta }(u,v)\right) ; \end{aligned}$$

(11)

$$\begin{aligned} {\hat{C}}_{\alpha ,\theta }(u,v)= &\, {} C_{\theta }(u,v)+\alpha \left( \text {M}(u,v)-C_{\theta }(u,v)\right) . \end{aligned}$$

(12)

• 1. ${\tilde{C}}_{\alpha ,\theta }(u,v)=C_{\theta (1-\alpha )}(u,v)$ - is a member of the Farlie–Gumbel–Morgenstern family of copulas and generates $\psi$-mixing Markov chains.

• 2. ${\hat{C}}_{\alpha ,\theta }(u,v)$ is not a member of the Farlie–Gumbel–Morgenstern family of copulas and does not generates $\psi$-mixing Markov chains, but generates $\psi '$-mixing Markov chains.

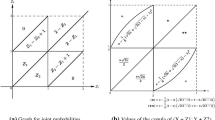
On Fig. 1 we have a 3-dimensional graph of the Farlie–Gumbel–Morgenstern copula with $\theta =0.6$ and its level curves on the left and the corresponding graphs for the perturbation with $\alpha =0.4$ on the right. Figure 2 represents a simulated Markov chain from the Farlie–Gumbel–Morgenstern copula with $\theta =0.4$ and the one generated by its perturbation with $\alpha =0.7$. Here, the marginal distribution of the Markov chain is the standard normal distribution. We can see on the graphs that the mixing structure is not the same when the copula is perturbed by M(u, v). This supports the theoretical results.

Fig. 1

Farlie–Gumbel–Morgenstern copula and level curves

Fig. 2

Data from the Farlie–Gumbel–Morgenstern copula and its perturbations

The Mardia family of copulas is defined by

$$\begin{aligned} C_{a,b}(u,v)=aM(u,v)+bW(u,v)+(1-a-b)\Pi (u,v) \end{aligned}$$

(13)

and the Frechet copulas form a subfamily with $a=\dfrac{\theta ^2(1+\theta )}{2}$, $b=\dfrac{\theta ^2(1-\theta )}{2}$ and $|\theta |\le 1$. Unlike Farlie–Gumbel–Morgenstern copulas, these copulas are not absolutely continuous. To generate an observation (U, V) from $C_{\theta }(u,v)$, one needs to generate independent observations $(U,V_1, V_2)$ from the uniform distribution on (0, 1). Then, do the following:

$$\begin{aligned} V=\left\{ \begin{array}{lcl} V_2 &{} \text {if}&{} V_1< 1-\theta ^2,\\ U &{} \text {if}&{} 1-\theta ^2<V_1<1-\theta ^2+\theta ^2(1+\theta )/2,\\ 1-U &{}\text {if}&{} V_1>1-\theta ^2+\theta ^2(1+\theta )/2. \end{array} \right. \end{aligned}$$

Fig. 3

Frechet copula representation and level curves

Figure 3 gives a representation of the Frechet copula for $\theta =0.6$ and its perturbation with $\alpha =0.4$ and their with level curves. Figure 4 represents a Markov chain of 500 observations simulated from the Frechet copula with $\theta =0.6$ and its perturbation with $\alpha =0.7$. Perturbations of the Frechet copula have the form given in Proposition 3.0.1.

Fig. 4

Markov chain generated by Frechet copulas and its perturbations

It is good to notice that these perturbations are not Frechet copulas, but remain in the class of Mardia copulas. Figure 4 represents a Markov chain generated by a Frechet copula and the one generated by its perturbation via a Farlie–Gumbel–Morgenstern copula using the standard normal distribution as stationary distribution.

4 Simulation Study

This simulation study shows the importance of the topic. We simulate a dependent data set that exhibits $\psi$-mixing or $\psi '$-mixing and show how the mixing structure influences the statistical study. Based on the fact that the considered mixing coefficient converges exponentially to 0, we can bound the variance of partial sums and obtain the condition of the central limit theorem and confidence interval of Longla and Peligrad [17]. Thanks to this central limit theorem, we construct confidence intervals without having to estimate the limiting variance of the central limit theorem of Kipnis and Varadhan [11] that holds here because the Markov chains are reversible and $n var({\bar{Y}})\rightarrow \sigma <\infty$. The standard central limit theorem is useless in this case because the limiting variance is not necessarily that of Y. Let us recall here the formulations of Longla and Peligrad [17]. They have proposed a new robust confidence interval for the mean based on a sample of dependent observations with a mild condition on the variance of partial sums. This confidence interval needs a random sample $(X_i, 1\le i\le n)$, generated independently of $(Y_i, 1\le i\le n)$ and following the standard normal distribution. The Gaussian Kernel and the optimal bandwidths $h_n$ are used. Denoting $\bar{y^2_n}$ the sample average of $Y^2$ and ${\bar{y}}_n$ the sample average of Y,

$$\begin{aligned} h_n=\left[ \dfrac{\bar{y^2_n}}{n\sqrt{2}{\bar{y}}^2_n}\right] ^{1/5}. \end{aligned}$$

Let’s check the conditions required for use of their proposed estimator of the mean and confidence interval. These conditions are as follows:

• 1. $(Y_i)_{i\in {\mathbb {Z}}}$ is an ergodic sequence;

• 2. $(Y_i)_{i\in {\mathbb {Z}}}$ have finite second moments;

• 3. $nh_n var({\bar{Y}}_n)\rightarrow 0$ as $n\rightarrow \infty$.

For the sake of clarity, we will use $C^{FGM}_\theta (u,v)$ to denote the Farlie–Gumbel–Morgenstern copula with parameter $\theta$.

Verification of the conditions

• 1. Ergodicity

  • (a) It has been shown in Theorem 2.3 and Example 2.4 of Longla [19] that the copula $C_{\theta }^{FGM}(u,v)$ generates geometrically ergodic Markov chains.

  • (b) Based on the results of this paper, we deduce that the perturbation copula ${\hat{C}}^{FGM}_{\theta ,\alpha }(u,v)$ generates $\psi '$-mixing Markov chains. In fact, this copula is a convex combination of two copulas such that one is $\psi '$-mixing. In addition, (see [5] and [21]) $\psi '$-mixing implies $\phi$-mixing and $\phi$-mixing implies geometric ergodicity for reversible Markov chains. So the Markov chain generated by ${\hat{C}}^{FGM}_{\theta ,\alpha }(u,v)$ is geometrically ergodic.

  • (c) By Theorem 2.16 and Remark 2.17 of Longla [19], the Frechet copula $C_\theta (u,v)$ generates geometrically ergodic Markov chains.

  • (d) The perturbation copula ${\hat{C}}_{(\theta _1,\theta _2,\alpha )}(u,v)$ is a convex combination of copulas $C_{\theta _1}(u,v)$ and $C^{FGM}_{\theta _2}(u,v)$. These two copulas are symmetric and each one generates geometrically ergodic stationary Markov chains as said above. Therefore, by Theorem 5 of Longla and Peligrad [21], this copula generates geometrically ergodic Markov chains.

• 2. The stationary distribution that is used in this paper is gaussian with mean 30 and variance 1. Therefore, variables have finite second moments.

• 3. The condition on the variance ($nh_n var({\bar{Y}})\rightarrow 0$) is checked in the appropriate section below.

For data simulation, we set $Y_i\sim N(30,1)$ for all copulas and the perturbation parameter $\alpha =0.4$ in all cases. For Farlie–Gumbel–Morgenstern and Frechet copulas we set $\theta =0.6$. For the Frechet perturbed copula, $\theta _1=\theta _2=0.6$. For $1\le i\le n$, $X_i\sim N(0,1)$ is a sequence of independent random variables that is independent of the Markov chain $(Y_i, 1\le i\le n)$.

Using the above mentioned, the estimator of $\mu _Y$ is ${\tilde{r}}_n=\dfrac{1}{nh_n}\sum \nolimits _{i=1}^nY_i \exp \left( -0.5(\dfrac{X_i}{h_n})^2\right)$ and the confidence interval is $\left( {\tilde{r}}_n\sqrt{1+h_n^2}-z_{\alpha /2}\left( \dfrac{\bar{Y_n^2}}{nh_n\sqrt{2}}\right) ^{1/2}, {\tilde{r}}_n\sqrt{1+h_n^2}+z_{\alpha /2}\left( \dfrac{\bar{Y_n^2}}{nh_n\sqrt{2}}\right) ^{1/2}\right)$.

The following Table 1 is the result of the simulation study for Markov chains generated by the considered copulas and their perturbations.

Table 1 Simulation study

5 Conclusion and Remarks

The graphs and simulations presented in this paper have been obtained using R. We have provided some insights on $\psi ^*$-mixing, $\psi '$-mixing and $\psi$-mixing. Though we have presented extensive examples and results for $\psi '$-mixing and $\psi ^*$-mixing, we have not been able to answer the question on convex combinations of $\psi$-mixing. The following question remains open: Does a convex combination of $\psi$-mixing generating copulas generate $\psi$-mixing? A positive answer to this question has been presented for the case when each of the copulas satisfy $\psi _1<1$.

6 List of Abbreviations

“$L_{2}$-norm of a function” stands for the square root of the integral of its square.

Appendix of Proofs

1.1 Proof of Theorem 2.1.1

Recall that the function c(x, y) defined on $I^2$ is said to be bounded away from zero on a set of Lebesgue measure 1 iff $\exists m>0, m\in {\mathbb {R}}, \exists Q\subset [0,1]^2: \lambda (Q)=1, \forall (x,y)\in Q$, $c(x,y)\ge m.$

By Bradley [6], a strictly stationary Markov chain $(X_k, ~ k\in {\mathbb {N}})$ is $\psi '$-mixing if $\text { for some } n\in {\mathbb {N}}, ~ \psi _n'(C)\ne 0.$ Let $A\subset [0,1],~ B\subset [0,1]$.

$$\begin{aligned} P(X_1\in A, X_2\in B)\ge & {} \int _A\int _Bc(x,y)dxdy\nonumber \\\ge & {} \int _A\int _B(\varepsilon _1(x)+\varepsilon _2(y))dxdy\nonumber \\= & {} \int _A\varepsilon _1(x)dx \lambda (B)+\int _B\varepsilon _2(y)dy\lambda (A)\nonumber \\ \end{aligned}$$

(14)

Thus, for all $A\subset [0,1],~ B\subset [0,1]$,

$$\begin{aligned} \dfrac{P(X_1\in A, X_2\in B)}{\lambda (A)\lambda (B)}\ge \dfrac{ \int _A\varepsilon _1(x)dx}{\lambda (A)}+\dfrac{\int _B\varepsilon _2(y)dy}{\lambda (B)}. \end{aligned}$$

(15)

Therefore,

$\underset{\underset{ \lambda (A)\lambda (B)>0}{ A\subset [0,1],~ B\subset [0,1]}}{\inf }P(X_1\in A , X_2\in B)\ge M,$ where $M=\min \bigg \{ \underset{\underset{\lambda (A)>0}{A\subset [0,1]}}{\inf }\dfrac{ \int _A\varepsilon _1d\lambda }{\lambda (A)}, \underset{\underset{\lambda (B)>0}{B\subset [0,1]}}{\inf }\dfrac{\int _B\varepsilon _2d\lambda }{\lambda (B)}\bigg \}$. Hence, $\psi '_1(C)\ge M>0.$ We can conclude $(X_k, k\in {\mathbb {N}})$ is $\psi '$-mixing.

1.2 Theorem 2.1.3 and 2.1.4

To prove these theorems, we will use the following proposition from Longla et al. [16]

Proposition 6.2.1

For a convex combination of copulas $C(x,y)=\sum _{i=1}^ka_i C_i(x,y),$ where $0<a_1,...,a_k<1$ and

$$\begin{aligned} \displaystyle \sum _{i=1}^k a_i=1\text {, for any }s\in {\mathbb {N}}\text { we have}\quad C^s(x,y)=\sum _{j=1}^{k^s}b_j\times ~_1C_j*...*~_sC_j(x,y), \end{aligned}$$

(16)

where $\sum _{j=1}^{k^s}b_j=1,~ 0<b_1,..., b_{k_s}<1$, and each of the copulas $~_iC_j(x,y)=C_{j_i}(x,y)$ for some $j_i\in \{1,..., k\}$ and the sum is over all possible products of s copulas selected from the original k copulas with replacement.

The notation $~_iC_j$ indicates that the copula $C_{j_i}$ was selected in the given $j\mathrm{th}$ element of $B= \{C_1,...,C_k\}^s$.

(1)   Suppose that there exists a subset of copulas $C_{k_1},...,C_{k_s}~, s\le k\in {\mathbb {N}}$ such that $\psi '({\hat{C}})>0$ for ${\hat{C}}=C_{k_1}*...*C_{k_s}$. Equation (16) can be written as follows:

$$\begin{aligned} C^s(x,y)=b_i {\hat{C}}(x,y)+\sum _{\underset{j\ne i}{j=1}}^{k^s}b_j {\hat{C}}_j(x,y), ~~~\text {where}\end{aligned}$$

(17)

${\hat{C}}(x,y)=C_{i_1}*...*C_{i_s}(x,y)$   and ${\hat{C}}_j(x,y)=C_{j_1}*...*C_{j_s}(x,y)$

Let $(X_k, k\in {\mathbb {N}})$ be a copula-based Markov chain generated by the copula C(x, y); $({\hat{X}}^j_k, k\in {\mathbb {N}})$ a copula-based Markov chain generated by the copula ${\hat{C}}_j$ for $1\le j \le k^s$, ${\hat{C}}_i={\hat{C}}$. For $A\in \sigma (X_0)$ and $B\in \sigma (X_s)$, Eq. (17) yields

$$\begin{aligned} P^s(A\cap B)= & {} b_i{\hat{P}}(A\cap B)+ \sum _{\underset{j\ne i}{j=1}}^{k^s}b_j {\hat{P}}_j(A\cap B)\ge b_i {\hat{P}}(A\cap B), \end{aligned}$$

(18)

where $P^s(A\cap B)= P(X_1\in A, X_{s+1}\in B)$; ${\hat{P}}_j(A\cap B)=P({\hat{X}}^j_1\in A, {\hat{X}}^j_{s+1}\in B)$ and ${\hat{P}}(A\cap B)=P({\hat{X}}^i_1\in A, {\hat{X}}^i_{s+1}\in B)$. Thus,

$\psi '_s(C)=\underset{A\subset I, B\subset I, P(A)(B)>0~}{\inf }\dfrac{P^s(A\cap B)}{P(A)P(B)}\ge b_i\psi '({\hat{C}})$.

By our assumptions, $\psi '({\hat{C}})>0$. The conclusion follows from Bradley [6].

(2)  Suppose there exists a subset of copulas $C_{k_1},...,C_{k_s}~, s\le k\in {\mathbb {N}}$ such that the density of the absolutely continuous part of the copula ${\hat{C}}=C_{k_1}*...*C_{k_s}$ is bounded away from zero. From Eq. (17) we have:

$$\begin{aligned} c^s(x,y)\ge b_i {\hat{c}}(x,y).\end{aligned}$$

(19)

Moreover, the density of the absolutely continuous part of ${\hat{C}}(u,v)$ is bounded away from zero. Thus, there exists $c>0$: $\forall (x,y)\in [0,1]^2$,  ${\hat{c}}(x,y)\ge c$ almost surely. Hence, from (19), we have $c^s(x,y)\ge b_i c$. Now, if $(X_k, k\in {\mathbb {N}})$ is a copula-based Markov chain generated by the copula C(x, y) and an absolutely continuous distribution, then for $A\in \sigma (X_1)$ and $B\in \sigma (X_{s+1})$, we have

$$\begin{aligned} P^s(A\cap B) \ge b_i c P(A)\times P(B) \quad \text { and } \quad \dfrac{P^s(A\cap B)}{P(A)\times P(B)} \ge b_i c , \end{aligned}$$

(20)

where $P^s(A\cap B)= P(X_1\in A, X_{s+1}\in B)$. It follows from Eq. (20) that

$$\begin{aligned} \displaystyle \psi '_s(C)=\underset{P(A)(B)>0~}{\inf }\dfrac{P^s(A\cap B)}{P(A)P(B)}\ge b_i c >0. \end{aligned}$$

This concludes the proof of Theorem 2.1.4.

1.3 Proof of Formula 5

The following representation is true for Farlie–Gumbel–Morgenstern copulas with $\lambda =1-\theta$.

$$\begin{aligned} C_{\theta }(u,v)=(1-\lambda ) (uv+uv(1-u)(1-v))+\lambda uv. \end{aligned}$$

Given that $C(u,v)=(uv+uv(1-u)(1-v))$ is a copula, we can apply [15] to obtain

$$\begin{aligned} C^n_\theta (u,v)=(1-\lambda )^nC^n(u,v)+(1-(1-\lambda )^n)uv. \end{aligned}$$

It remains to show that $C^n(u,v)=uv+3(\frac{1}{3})^n uv(1-u)(1-v)$ by mathematical induction. It is clear that the formula is correct for $n=1$. Assume that for $n=k$, we have

$$\begin{aligned} C^k(u,v)=uv+3\left( \frac{1}{3}\right) ^k uv(1-u)(1-v). \end{aligned}$$

Using the fold product, we obtain

$$\begin{aligned} C^{k+1}= & \, {} C^{k}*C(u,v)=\int _0^1C^k_{,2}(u,t)C_{,1}(t,v)dt, \\ \text {where}\quad C^k_{,2}(u,t)= & {} \, u+3(\frac{1}{3})^k u(1-u)(1-2t) \quad \\ \text {and} \quad C_{,1}(t,v)= & \, {} v+v(1-v)(1-2t). \end{aligned}$$

Plugging these functions into the integral and computing yields the needed result. The proof ends by replacing $C^n(u,v)$ by its value and $\lambda =1-\theta$.

1.4 Proof of Theorem 2.2.3

Assume that the copula C(u, v) is such that for all $(u,v)\in [0,1]^2$, $c^n(u,v)\le K$, where K is a constant and $c^n$ is the density of the copula $C^n(u,v)$. Let $A\in \sigma (X_0)$ and $B\in \sigma (X_n)$, where $(X_0,X_n)$ has copula $C^n(u,v)$. Assume that the stationary distribution of the Markov chain has distribution F(x). Using Sklar’s Theorem (see [27]), we have

$$\begin{aligned} P^n(A\cap B)=P(X_0\in A , X_n\in B)=\int _A\int _{B}c^n(F(x), F(y))dF(y)dF(x). \end{aligned}$$

Therefore, $P^n(A \cap B)\le KP(A)P(B)$. It follows that $\psi ^*_n(C)\le K$. Moreover,

• 1. if $c^s(u,v)$ is bounded away from 0, then by Longla [18] C(u, v) generates $\psi '$-mixing stationary Markov chains. This implies the these Markov chains are mixing in the ergodic theoretic sense. Therefore, as $\psi _n^*(C)\le K\ne \infty$, Bradley [6] implies that C(u, v) generates stationary $\psi ^*$-mixing Markov chains.

• 2. if $c^n(u,v)\le m<2$ for all $(u,v)\in [0,1]^2$, then it follows $P^n(A\cap B)\le m P(A)P(B)$. It follows that $\psi ^*_n(C)\le m<2$. This inequality implies $\psi$-mixing without extra condistions by Theorem 3.3. of Bradley [5].

• 3. Now, if we assume that there exists a set of non-zero measure $\Omega \subset [0,1]^2$ such that $A\times B\subset \Omega$, $A\in \sigma (X_0)$, $B\in \sigma (X_n)$ and the density of $C^n(u,v)$ is not bounded above on $\Omega$, but bounded below by a any given non-zero real number M. This construction is possible due to continuity of the density of C(u, v). It follows that for any constant M,

  $$\begin{aligned} P^n(X_0\in A ,X_n\in B)\ge M \int _{A\times B}dF(x)dF(y)=MP(A)P(B). \end{aligned}$$

  It is obvious here that As M grows, the size of P(A)P(B) reduces as their product has to be at most 1. From here, we obtain

  $$\begin{aligned} \frac{P(A\cap B)}{P(A)P(B)}\ge M. \quad \text {This leads to }\quad \psi ^*_n(C)>M. \end{aligned}$$

  Because this is true for every M and n, we can conclude that $\psi ^*_n(C)=\infty$ and $\psi _n(C)=\infty$ for all n. Thus, the generated Markov chain is not $\psi$-mixing.

1.5 Proof of Theorem 2.2.10 and Theorem 2.2.11

Without loss of generality the proof can be done for a convex combination of two copulas, one of which is C(u, v) and doesn’t generate $\psi ^*$-mixing Markov chains. This is true because any convex combination of copulas can be written as a convex combination of two copulas. Now, assume that

$$\begin{aligned} C_2(u,v)=\alpha C(u,v)+(1-\alpha )C_1(u,v). \end{aligned}$$

By Bradley [6], $\psi ^*_n(C)=\infty$ for all $n\in {\mathbb {N}}$. We need to show that $\psi ^*_n(C_2)=\infty$ for all $n\in {\mathbb {N}}$. By Longla et al. [15], there exist $b_{in}, C_{1in}(u,v)$, such that $b_{in}>0$, $\alpha ^n+\sum _{i=2}^{2^n}b_{in}=1$ and

$$\begin{aligned} C_2^{n}(u,v)=\sum _{i=2}^{2^n} b_{in} C_{1in}(u,v)+\alpha ^n C^n(u,v). \end{aligned}$$

Therefore, the probability distribution $P^{n}_2$ of $(X_1, X_{n+1})$ for the Markov chain generated by $C_2(u,v)$ and the probability distributions $P^n_{1i}$ of $({\tilde{X}}_{i1},{\tilde{X}}_{in+1})$ for the Markov chains generated by the copulas $C_{1in}(u,v)$ satisfy the following relationship for every $A\in \sigma (X_0)$ and $B\in \sigma (X_{n+1})$:

$$\begin{aligned} P_2^{n}(A\cap B)=\sum _{i=2}^{2^n} b_{in} P^n_{1i}(A\cap B)+\alpha ^n P^n(A\cap B). \end{aligned}$$

Therefore, $P_2^n(A\cap B)\ge \alpha ^nP^n(A\cap B)$. Given that $\psi ^*_n(C)=\infty$ for all n, it follows that $\sup _{A,B}\frac{P^n(A\cap B)}{P(A)P(B)}=\infty$, leading to

$$\begin{aligned} \sup _{A,B}\frac{P^n_2(A\cap B)}{P(A)P(B)}=\infty \quad \text {and} \quad \psi ^*_n(C_2)=\infty \quad \text {for all}\quad n\in {\mathbb {N}}. \end{aligned}$$

This concludes the proof of Theorem 2.2.10.

Now, to prove Theorem 2.2.11, as for the previous case, it is enough to consider a convex combination of two copulas. Assume that $C_1(u,v)$ and $C_2(u,v)$ generate each $\psi ^*$-mixing stationary copula-based Markov chains with $\psi ^*_1<2$. Define $C(u,v)=\alpha C_1(u,v)+(1-\alpha )C_2(u,v)$. Once more, we use [6] to establish that we have $\psi ^*$-mixing. By Longla et al [15] we have $\psi ^*_1(C)\le \alpha \psi _1(C_1)+(1-\alpha ) \psi _1(C_2)$. Therefore, $\psi ^*_1(C)<2(\alpha )+2(1-\alpha )=2$. To finish the proof, we need to show that the Markov chain generated by the convex combination is mixing. Each of the copulas generates mixing stationary Markov chains because these Markov chains are $\psi ^*$-mixing. Therefore, their convex combination generates mixing stationary Markov chains as shown by Longla [18].

1.6 Checking the Condition $nh_n var({\bar{Y}})\rightarrow 0$

Given the Markov chains that we consider are reversible and ergodic (see [9, 11]),

$$\begin{aligned} n var({\bar{Y}})\quad \text {behaves as}\quad var(Y_0)+2\sum _{k=1}^\infty cov(Y_0, Y_k). \end{aligned}$$

Moreover, if the series converges, then the central limit theorem holds with variance equal to its sum. On the other side, Markov chains generated by Farlie–Gumbel–Morgenstern copulas, Frechet copulas and their considered perturbations are exponential $\psi '$-mixing. This implies that they are all exponential $\rho$-mixing. Exponential $\rho$-mixing implies convergence of the considered series. Therefore $n var({\bar{Y}})\rightarrow C$, leading to $nh_n var({\bar{Y}})\rightarrow 0$.