Exact Moments of Order Statistics and Parameter Estimation for Sushila Distribution

Abstract

In this paper, we have obtained the exact expression and recurrence relations for single moments of order statistics arising from Sushila distribution. We have also obtained L-moments, TL-moments of Sushila distribution and used them to find the L-moment and TL-moment estimators of the parameters of the distribution. The estimators of the parameters are also obtained using the method of moments and maximum likelihood. Further, by using these maximum likelihood estimators (MLEs), we have also obtained the MLEs of the measures of reliability of the considered distribution. Monte Carlo simulation has been carried out to investigate the performance of the estimators.

1 Introduction

Lindley distribution was proposed by Lindley [14] in the context of Bayesian statistics, as a counter example of fiducial statistics. However, due to the popularity of the exponential distribution in statistics especially in reliability theory, Lindley distribution has been overlooked in the literature. Recently, many authors have paid great attention to the Lindley distribution as a lifetime model. From different point of view, Ghitany et al. [8] showed that Lindley distribution is a better lifetime model than exponential distribution.

Shanker et al. [21] generalized the Lindley distribution by adding a new parameter, i.e., they introduced a two-parameter continuous distribution, with parameters α and λ, named ‘Sushila distribution (SD(α,λ))’,with its probability density function (pdf) given as

$$f\left(x\right)= \frac{{\alpha }^{2}}{\lambda \left(1+\alpha \right)}\left(1+\frac{x}{\lambda }\right){e}^{-\frac{\alpha }{\lambda }x} , x>0,\lambda > 0,\alpha > 0,$$

(1)

and the cumulative distribution function (cdf) as

$$F\left(x\right)=1- \left(1+\frac{\alpha x}{\lambda \left(1+\alpha \right)}\right){e}^{-\frac{\alpha }{\lambda }x} , x>0,\lambda > 0,\alpha > 0.$$

(2)

The corresponding hazard function of the distribution is thus given by

$$h\left(x\right)= \frac{{\alpha }^{2}(\lambda +x)}{\lambda \left[\lambda \left(1+\alpha \right)+\alpha x\right]} , x>0,\lambda > 0,\alpha > 0.$$

(3)

It can easily be seen that Lindley distribution (LD) is a particular case of (1) for λ = 1. Shanker et al. [21] have studied several properties of Sushila distribution such as moments, failure rate function, mean residual life function etc. They have done comparative study using data sets relating to waiting times, to test its goodness of fit to which earlier the LD has been fitted and it was found that the Sushila distribution provides better fits than those by the LD.

The pdf (1) can be shown as a mixture of $\mathrm{gamma} \left(1, \frac{\alpha }{\lambda } \right)$ i.e. $\mathrm{exp} \left(\frac{\alpha }{\lambda } \right)$ and $\mathrm{gamma} \left(2, \frac{\alpha }{\lambda } \right)$ distributions as follows:

$$f\left(x\right)={pg}_{1}\left(x\right)+{\left(1-p\right)g}_{2}\left(x\right),$$

where,

$$p=\frac{\alpha }{1+\alpha }, {g}_{1}\left(x\right)= \frac{\alpha }{\lambda }{e}^{-\frac{\alpha }{\lambda }x}, {g}_{2}\left(x\right)={ \left(\frac{\alpha }{\lambda } \right)}^{2}x{e}^{-\frac{\alpha }{\lambda }x}.$$

We have utilized this fact in drawing random samples from Sushila distribution for simulation purpose.

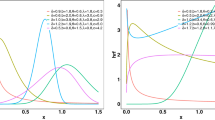
The graph of density function of Sushila distribution for different values of the parameters α and λ is provided in Fig. 1.

Fig. 1

pdf of Sushila distribution

1.1 Moments and Related Measures

The ${r}$th moment about origin of the Sushila distribution, defined in (1), is given as

$${\mu }_{r}^{\prime}= \frac{{\alpha }^{2}}{\lambda (1+\alpha )}\underset{0}{\overset{\infty }{\int }}{x}^{r}\left(1+\frac{x}{\lambda }\right){e}^{\frac{-\alpha x}{\lambda }}dx={\left(\frac{\lambda }{\alpha }\right)}^{r}\left(\frac{\alpha +r+1}{\alpha +1}\right)r! , \quad r= 1,2,3,\ldots $$

(4)

Taking $r= 1, 2, 3 \;\mathrm{and} \; 4$ in (4), the first four moments (about origin) of a random variable (r.v.) $X\sim SD(\alpha ,\lambda )$ are obtained as

$${\mu }_{1}^{\prime}= \frac{\lambda (\alpha +2)}{\alpha (\alpha +1)} , {\mu }_{2}^{\prime}=\frac{2{\lambda }^{2}(\mathrm{\alpha }+3)}{{\alpha }^{2}(\mathrm{\alpha }+1)} , {\mu }_{3}^{\prime}= \frac{6{\lambda }^{3}(\mathrm{\alpha }+4)}{{\alpha }^{3}(\mathrm{\alpha }+1)} ,{\mu }_{4}^{\prime}= \frac{24 {\lambda }^{4}(\mathrm{\alpha }+5)}{{\alpha }^{4}(\mathrm{\alpha }+1)} .$$

(5)

The central moments of the distribution are thus obtained as

$${\mu }_{2}= \frac{ {\lambda }^{2}({\alpha }^{2}+4\mathrm{\alpha }+2)}{{\alpha }^{2}{(\mathrm{\alpha }+1)}^{2}}, {\mu }_{3}= \frac{2 {\lambda }^{3}({\alpha }^{3}+6{\alpha }^{2}+6\mathrm{\alpha }+2)}{{\alpha }^{3}{(\mathrm{\alpha }+1)}^{3}}, {\mu }_{4}= \frac{3 {\lambda }^{4}({3\alpha }^{4}+{24\alpha }^{3}+44{\alpha }^{2}+32\mathrm{\alpha }+8)}{{\alpha }^{4}{(\mathrm{\alpha }+1)}^{4}}.$$

(6)

Therefore, mean, variance, skewness ($\sqrt{{\beta }_{1}})$ and kurtosis (${\beta }_{2})$ of a r.v. $X\sim SD(\alpha ,\lambda )$ are, respectively, given by

$$\mathrm{Mean}= \frac{\lambda (\alpha +2)}{\alpha (\alpha +1)} , \mathrm{Variance}=\frac{ {\lambda }^{2}({\alpha }^{2}+4\mathrm{\alpha }+2)}{{\alpha }^{2}{(\mathrm{\alpha }+1)}^{2}},$$

$$\sqrt{{\beta }_{1}}= \frac{{\mu }_{3}}{{ {\mu }_{2}}^{3/2}}=\frac{2({\alpha }^{3}+6{\alpha }^{2}+6\mathrm{\alpha }+2)}{{({\alpha }^{2}+4\mathrm{\alpha }+2)}^{3/2}} \mathrm{and} \; {\beta }_{2}=\frac{{\mu }_{4}}{{ {\mu }_{2}}^{2}}= \frac{3 ({3\alpha }^{4}+{24\alpha }^{3}+44{\alpha }^{2}+32\mathrm{\alpha }+8)}{{({\alpha }^{2}+4\mathrm{\alpha }+2)}^{2}} .$$

(7)

The graphs of skewness and kurtosis are provided in Figs. 2 and 3, respectively.

Fig. 2

Skewness of Sushila distribution

Fig. 3

Kurtosis of Sushila distribution

Remark 1.

From Eq. (7) we observe that both skewness $(\sqrt{{\beta }_{1}})$ and kurtosis (${\beta }_{2})$ are independent of the parameter λ, i.e., these are functions of parameter α only.

Remark 2.

The roots of Eq. ${\alpha }^{2}+4\mathrm{\alpha }+2$ = 0 are α = $-2\pm$ √2, both the values being negative, therefore expressions for both $\sqrt{{\beta }_{1}}$ and ${\beta }_{2}$ in (7) are well defined for all α > 0.

Let ${X}_{1}$, ${X}_{2}$, … , ${X}_{n}$ be a random sample of size n from Sushila distribution defined in (1) and let ${X}_{1:n}$ ≤ ${X}_{2:n}$  ≤ … ≤ ${X}_{n:n}$ be the corresponding order statistics. Then the probability density function (pdf) of ${X}_{r:n}$ (1 ≤ r ≤ n) is given by

$${f}_{r:n}\left(x\right)= {C}_{r:n}{\left[F\left(x\right)\right]}^{r-1}{\left[1-F\left(x\right)\right]}^{n-r}f\left(x\right) , 0\le x<\infty ,$$

(8)

where $f\left(x\right) \; \mathrm{and} \; F(x)$ are given by (1) and (2), respectively, and ${C}_{r:n}$ = $\frac{n!}{(r-1)!\left(n-r\right)!}$.

Similarly, the joint density function of order statistics ${X}_{r:n} \; \mathrm{and } \; {X}_{s:n}$(1 ≤ r < s ≤ n) is given by

$${f}_{r,s:n}\left(x,y\right)={C}_{r,s:n}{[F\left(x\right)]}^{r-1}{[F\left(y\right)-F\left(x\right)]}^{s-r-1}{ [1-F\left(y\right)]}^{n-s} f\left(x\right)f\left(y\right), 0 \le x<y<\infty ,$$

(9)

where ${C}_{r,s:n}= \frac{n!}{\left(r-1\right)!\left(s-r-1\right)!\left(n-s\right)!}$

(cf. [5]).

The single moments of order statistics ${X}_{r:n}(1\le r\le n)$ are given by

$${ \mu }_{r:n}^{(k)}=E\left({X}_{r:n}^{k}\right)= \underset{0}{\overset{\infty }{\int }}{x}^{k}{f}_{r:n}\left(x\right)dx, k=\mathrm{0,1},2,\ldots .$$

(10)

Similarly, the product moments of ${X}_{r:n} \; \mathrm{and } \; {X}_{s:n}\left(1\le r<s\le n\right)$ are given by

$${\mu }_{r,s:n}^{(j,k)}=E \left({X}_{r:n}^{j}{X}_{s:n}^{k}\right)=\underset{0}{\overset{\infty }{\int }}\underset{x}{\overset{\infty }{\int }}{x}^{j}{y}^{k}{f}_{r,s:n}\left(x,y\right)dydx j,k=\mathrm{0,1},2,\ldots .$$

(11)

One can observe from (1) and (2) that the characterizing differential equation for the case of Sushila distribution is given by

$$\left(\lambda \left(1+\alpha \right)+\alpha x\right)f\left(x\right)={\alpha }^{2}\left(1+\frac{x}{\lambda }\right)\left(1-F\left(x\right)\right).$$

(12)

In this paper, in Sect. 2, we have obtained exact expression and recurrence relations for single moments of order statistics from Sushila distribution. In Sects. 3 and 4, we have estimated parameters α and λ using methods of L-moments, TL-moments and method of moments. In Sect. 5, we have obtained the MLEs of α and λ, and hence the MLEs of the reliability functions $R(t)$ and P. In Sect. 6, simulation study is carried out to investigate the performance of the estimators.

2 Exact Expression and Recurrence Relations for Single Moments of Order Statistics from Sushila Distribution

In this section we shall establish explicit expression for single moments of order statistics from Sushila distribution as discussed in Sect. 1. Further, this result is used to evaluate the first four moments of order statistics and are presented in Tables 1 and 2. We shall also establish recurrence relations for single moments of order statistics from Sushila distribution.

Table 1 Values of ${\mu }_{r:n}^{(1)} \equiv { \mu }_{r:n} ,\mathrm{for}\, 1\le n \le 4, \alpha = 2 \text{and\, for\, different\, values of\,}\, \lambda$

Table 2 Values of ${\mu }_{r:n}^{(2)} ,\mathrm{for}\, 1\le n \le 4, \alpha = 2\, \text{and different values of}\,\, \lambda$

Theorem 1

For Sushila distribution, as given in (1) and for 1 ≤ r ≤ n, k ≥ 1, we have

$${\mu }_{r:n}^{(k)}=E\left({X}_{r:n}^{k}\right)={\frac{{\lambda }^{k}}{{\alpha }^{k-1}} C}_{r:n}\sum_{i=0}^{n-r}\sum_{j=0}^{i+r-1}\sum_{m=0}^{j}\left(\genfrac{}{}{0pt}{}{n-r}{i}\right)\left(\genfrac{}{}{0pt}{}{i+r-1}{j}\right)\left(\genfrac{}{}{0pt}{}{j}{m}\right){\left(-1\right)}^{\left(i+j\right)}$$

$$\times \frac{1}{{\left(\alpha +1\right)}^{m+1}{\left(j+1\right)}^{k+m+1}}\left[\Gamma \left(\mathrm{k}+\mathrm{m}+1\right)+ \frac{\Gamma \left(\mathrm{k}+\mathrm{m}+2\right)}{\alpha \left(j+1\right)} \right],$$

(13)

where $\mathrm{\Gamma} \left(a\right)=\underset{0}{\overset{\infty }{\int }}{x}^{a-1}{e}^{-x}dx,$ is a Gamma function.

Proof

Using (10), we have

$${\mu }_{r:n}^{(k)}=E({{X}_{r:n}^{k})=C}_{r:n}\underset{0}{\overset{\infty }{\int }}{x}^{k}f(x)({F(x))}^{r-1}(1-{F(x))}^{n-r}dx.$$

Expanding $(1-{F(x))}^{n-r}$ binomially and substituting the values of $f(x)$ and $F(x)$ from (1) and (2), we get

$${\mu }_{r:n}^{\left(k\right)}={C}_{r:n}\frac{{\alpha }^{2}}{\lambda \left(1+\alpha \right)}\sum_{i=0}^{n-r}\left(\genfrac{}{}{0pt}{}{n-r}{i}\right){(-1)}^{i}\underset{0}{\overset{\infty }{\int }}{x}^{k} \left(1+\frac{x}{\lambda } \right){e}^{-\frac{\alpha }{\lambda }x}{\left(1-\left(1+\frac{\alpha x}{\lambda \left(1+\alpha \right)}\right) {e}^{-\frac{\alpha }{\lambda }x} \right)}^{i+r-1}dx .$$

Binomial expansion of ${ \left(1-\left(1+\frac{\alpha x}{\lambda \left(1+\alpha \right)}\right) {e}^{-\frac{\alpha }{\lambda }x} \right)}^{i+r-1}$, followed by further simplification leads to the desired result (13).$\square$

Remark 3.

Expression for single moments in Eq. (13), for k = 1, will be helpful to find the explicit expressions for L-moments and TL-moments from the considered distribution, as discussed in Sects. 3.1 and 3.3.

Remark 4.

Utilizing the result in (13) one can find the values of ${\mu }_{r:n}^{(k)}$(1 ≤ r ≤ n, k ≥ 1) for different values of α and λ. In particular for k = 1 and 2, we have calculated the values of ${\mu }_{r:n}^{(k)}$ and presented them in Table 1 and 2, respectively.

Theorem 2

$For \; 1<r\le n , k >0 \; and \; \alpha , \lambda >0, \; we\; have$

$$\lambda \left(1+\alpha \right){\mu }_{r:n}^{\left(k\right)}+\alpha {\mu }_{r:n}^{\left(k+1\right)}={\alpha }^{2}\frac{(n-r+1)}{(k+1)}\left[{\mu }_{r:n}^{\left(k+1\right)}-{\mu }_{r-1:n}^{\left(k+1\right)}\right]{+\alpha }^{2}\frac{(n-r+1)}{\lambda (k+2)}\left[{\mu }_{r:n}^{\left(k+2\right)}-{\mu }_{r-1:n}^{\left(k+2\right)}\right],$$

(14)

$$and\; for\; r=1, n \ge 1, k>0 \; and\; \alpha , \lambda >0, \; we \; have$$

$$\lambda \left(1+\alpha \right){\mu }_{1:n}^{\left(k\right)}+\alpha {\mu }_{1:n}^{\left(k+1\right)}=n{\alpha }^{2}\left[\frac{{\mu }_{1:n}^{\left(k+1\right)}}{(k+1)}+\frac{{\mu }_{1:n}^{\left(k+2\right)}}{\lambda (k+2)}\right].$$

(15)

Proof

Using (10), consider

$$\lambda \left(1+\alpha \right){\mu }_{r:n}^{\left(k\right)}+\alpha {\mu }_{r:n}^{\left(k+1\right)}= {C}_{r:n}\underset{0}{\overset{\infty }{\int }}{x}^{k}\left(\lambda \left(1+\alpha \right)+x\alpha \right)f(x)({F(x))}^{r-1}(1-{F(x))}^{n-r}dx.$$

(16)

Using the characterizing differential equation as given by (12) in (16), we get

$$\lambda \left(1+\alpha \right){\mu }_{r:n}^{\left(k\right)}+\alpha {\mu }_{r:n}^{\left(k+1\right)}={\alpha }^{2}{C}_{r:n}\left[{I}_{r:n}^{(k)}+\frac{1}{\lambda }{I}_{r:n}^{(k+1)}\right] ,$$

(17)

where

$${I}_{r:n}^{(k)}= \underset{0}{\overset{\infty }{\int }}{x}^{k}({F(x))}^{r-1}(1-{F(x))}^{n-r+1}dx .$$

Integrating by parts and simplifying, we get

$${ I}_{r:n}^{(k)}=\frac{n-r+1}{k+1} \frac{{\mu }_{r:n}^{(k+1)}}{{C}_{r:n}}-\frac{r-1}{k+1} \frac{{\mu }_{r-1:n}^{\left(k+1\right)}}{{C}_{r-1:n}}.$$

(18)

Using (18), substituting the values of ${I}_{r:n}^{(k)}$ and ${I}_{r:n}^{(k+1)}$ in (17), and after some simplification we get the desired result as given in (14).

Result in Eq. (15), for $r=1,$ can be proved on similar lines.$\square$

3 L-Moments and TL-Moments

It may be mentioned that Hosking [10] introduced the L-moments as a linear combination of probability weighted moments. Similar to ordinary moments, L-moments can also be used for parameter estimation, interval estimation and hypothesis testing. Hosking has shown that first four L-moments of a distribution measure, respectively, the average, dispersion, symmetry and tail weight (or peakedness) of the distribution. L-moments have turned out to be a popular tool in parametric estimation and distribution identification problems in different scientific areas such as hydrology in the estimation of flood frequency, climatology and meteorology in the research of extreme precipitation, etc. (cf. e.g. [4, 10, 11, 23]).

In comparison to the conventional moments, L-moments have lower sample variances and are more robust against outliers. For example, ${L}_{1}$ is the same as the population mean, is defined in terms of a conceptual sample of size $r=1,$ while ${L}_{2}$ is an alternative to the population standard deviation, is defined in terms of a conceptual sample of size $r=2.$ Similarly, the L-moments ${L}_{3}$ and ${L}_{4}$ are alternatives to the un-scaled measures of skewness and kurtosis ${\mu }_{3}$ and ${\mu }_{4}$, respectively (cf. [22]). Elamir and Seheult [7] introduced an extension of L-moments and called them TL-moments (trimmed L-moments). TL-moments are more robust than L-moments and exist even if the distribution does not have a mean, for example the TL-moments exist for Cauchy distribution (cf. [2, 19]). Abdul-Moniem [1] derived L-moments and TL-moments for the exponential distribution. Similar work has been done by Shahzad and Asghar [20] for Dagum distribution, by Saran et al. [18] for Lindley distribution, etc. Recently, Dutang [6] derived new closed-form formulas of L-moments and TL-moments for continuous probability distributions.

3.1 Methodology for L-Moments for Sushila Distribution

Let ${X}_{1}$, ${X}_{2}$, …, ${X}_{n}$ be a random sample from Sushila distribution as defined in (1) and ${X}_{1:n}$≤ ${X}_{2:n}$≤ … ≤ ${X}_{n:n}$ denote the corresponding order statistics. Then, the theoretical rth L-moment defined by Hosking [10] from the expectations of order statistics is as follows:

$${L}_{r }= \frac{1}{r} \sum_{k=0}^{r-1}{\left(-1\right)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)E\left({X}_{r-k:r}\right),$$

(19)

where

$$\mathrm{E}\left({X}_{i:r}\right)=\frac{r!}{\left(i-1\right)!\left(r-i\right)!}\underset{0}{\overset{\infty }{\int }}x{\left[F\left(x\right)\right]}^{i-1}{\left[1-F\left(x\right)\right]}^{r-i}f\left(x\right)dx.$$

(20)

For r = 1, 2, 3, 4 in (19), the first four L-moments are obtained as follows:

$${L}_{1}=E\left({X}_{1:1}\right)={\mu }_{1:1}$$

(21)

$${ L}_{2}=\frac{1}{2}E\left({X}_{2:2}-{X}_{1:2}\right)=\frac{1}{2}\left({\mu }_{2:2}-{\mu }_{1:2}\right)$$

(22)

$${L}_{3}=\frac{1}{3}E\left({X}_{3:3}-2{X}_{2:3}+{X}_{1:3}\right)=\frac{1}{3}\left({\mu }_{3:3}-2{\mu }_{2:3}+{\mu }_{1:3}\right)$$

(23)

$${L}_{4}=\frac{1}{4}E\left({X}_{4:4}-3{X}_{3:4}+3{X}_{2:4}-{X}_{1:4}\right)=\frac{1}{4}\left({\mu }_{4:4}-3{\mu }_{3:4}+3{\mu }_{2:4}-{\mu }_{1:4}\right)$$

(24)

Utilizing (13), for k = 1, we obtain the single moments of order statistics which are required in Eqs. (21)–(24) and thus we obtain the L-moments of the Sushila distribution as:

$${L}_{1}=\frac{\lambda (\alpha +1)}{\alpha (\alpha +2)}$$

(25)

$${ L}_{2}=\frac{\lambda }{4\alpha {\left(\alpha +1\right)}^{2}}\left(2{\alpha }^{2}+6\alpha +3\right)$$

(26)

$${ L}_{3}=\frac{\lambda }{648\alpha {(\alpha +1)}^{3}}\left(2{88\alpha }^{3}+1314{\alpha }^{2}+1713\alpha +751\right).$$

(27)

It may be mentioned that one can similarly obtain an expression for ${L}_{4}$ which has been omitted here due to its lengthy form.

In particular, ${L}_{1}, { L}_{2},{ L}_{3}$ and ${L}_{4}$ are population measures of the location, scale, skewness and kurtosis, respectively.

The L-skewness ${\tau }_{3}$ of Sushila distribution is given as

$${\tau }_{3}=\frac{{L}_{3}}{{L}_{2}}=\frac{2{88\alpha }^{3}+1314{\alpha }^{2}+1713\alpha +751}{162(\alpha +1)(2{\alpha }^{2}+6\alpha +3)}.$$

(28)

$$\mathrm{Also}, \; \mathrm{ one \; can\; calculate \; L}-\mathrm{kurtosis }\; {\tau }_{4} \; \mathrm{by \; solving }\; {\tau }_{4}=\frac{{L}_{4}}{{L}_{2}} .$$

3.2 Sample L-Moments and L-Moment Estimators

The L-moments can be estimated from the sample order statistics as follows (cf. [3]):

$${ l}_{r}=\frac{1}{r\left(\genfrac{}{}{0pt}{}{n}{r}\right)}\sum_{i=1}^{n}\sum_{k=0}^{r-1}{(-1)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)\left(\genfrac{}{}{0pt}{}{i-1}{r-k-1}\right)\left(\genfrac{}{}{0pt}{}{n-i}{k}\right){x}_{i:n}.$$

(29)

From Eq. (29) for $r=$ 1, 2 we get the sample L-moments ${l}_{1}\; \mathrm{and} \; {l}_{2}$. Equating sample L-moments with the population L-moments ${L}_{1 } \; \mathrm{and}\; {L}_{2}$, as given by Eqs. (25) and (26), respectively, we get

$${l}_{1}= \frac{1}{n} \sum_{i=1}^{n}{x}_{i:n}=\overline{x }= \frac{\lambda (\alpha +1)}{\alpha (\alpha +2)} ,$$

(30)

$${l}_{2}= \frac{2}{n(n-1)} \sum_{i=1}^{n}{(i-1)x}_{i:n}-\overline{x }= \frac{\lambda }{4\alpha {\left(\alpha +1\right)}^{2}} \left(2{\alpha }^{2}+6\alpha +3\right). $$

(31)

By solving (30) and (31) simultaneously, using program in R, we have obtained the L-moment estimators (${\widehat{\mathrm{\alpha }}}_{\mathrm{LM}} \; \mathrm{and } \; {\stackrel{\sim }{\uplambda }}_{\mathrm{LM}}$) of the parameters α and λ of Sushila distribution, which are calculated and presented in columns 2nd and 6th in Tables 6, 7, 8 and 9, for different values of α and λ.

3.3 Methodology for TL-Moments (Trimmed L-Moments) for Sushila Distribution

Elamir and Seheult [7] introduced some robust modification of Eq. (19) (and called it as TL-moments) in which E(${X}_{r-k:r}$) is replaced by E(${X}_{r+{t}_{1}-k:r+{t}_{1}+{t}_{2}}$) for each r where ${t}_{1}$ smallest and ${t}_{2}$ largest are trimmed from the conceptual sample. The following formula gives the rth TL-moments (cf. [7]):

$${ L}_{r}^{({t}_{1},{t}_{2})} = \frac{1}{r} \sum_{k=0}^{r-1}{\left(-1\right)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)\mathrm{E}({X}_{r+{t}_{1}-k:r+{t}_{1}+{t}_{2}}).$$

(32)

One can observe that TL-moments are more robust than L-moments and exist even if the distribution does not have a mean, for example the TL-moments exist for Cauchy distribution (cf. [2]). TL-moments reduce to L-moments when ${t}_{1}$ = 0 and ${t}_{2}$ = 0.

TL-moments given by (32) with ${t}_{1}$ = 1 and ${t}_{2}$ = 0 is defined as ${L}_{r}^{(1,0)}$ ≡ ${L}_{r}^{(1)}$:

$${L}_{r}^{(1)} = \frac{1}{r} \sum_{k=0}^{r-1}{\left(-1\right)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)\mathrm{E}({X}_{r+1-k:r+1}).$$

(33)

For r = 1, 2, 3 and 4 in (33), the above formula gives the first four TL-moments as follows:

$${L}_{1}^{(1)}=E\left({X}_{2:2}\right)={\mu }_{2:2}$$

(34)

$${L}_{2}^{(1)}=\frac{1}{2}E\left({X}_{3:3}-{X}_{2:3}\right)=\frac{1}{2}\left({\mu }_{3:3}-{\mu }_{2:3}\right)$$

(35)

$${L}_{3}^{(1)}=\frac{1}{3}E\left({X}_{4:4}-2{X}_{3:4}+ {X}_{2:4}\right)=\frac{1}{3}\left({\mu }_{4:4}-2{\mu }_{3:4}+ {\mu }_{2:4}\right)$$

(36)

$${L}_{4}^{(1)}=\frac{1}{4}E\left({X}_{5:5}-3{X}_{4:5}+3{X}_{3:5}-{X}_{2:5}\right)=\frac{1}{4}({\mu }_{5:5}-3{\mu }_{4:5}+3{\mu }_{3:5}-{\mu }_{2:5}).$$

(37)

Utilizing (13), for k = 1, we obtain the single moments of order statistics which are required in Eqs. (34)–(37) and thus we obtain the TL-moments of Sushila distribution as:

$${L}_{1}^{(1)}=\frac{\lambda }{4\alpha {\left(\alpha +1\right)}^{2}}\left(6{\alpha }^{2}+18\alpha +11\right), $$

(38)

$${L}_{2}^{\left(1\right)}=\frac{\lambda }{36\alpha {\left(\alpha +1\right)}^{3}}\left(18{\alpha }^{3}+72{\alpha }^{2}+75\alpha +25\right), $$

(39)

$${L}_{3}^{(1)}=\frac{\lambda }{10368\alpha {\left(\alpha +1\right)}^{4}}\left(60768{\alpha }^{4}+303840{\alpha }^{3}+580296{\alpha }^{2}+503812\alpha +163105\right).$$

(40)

It may be mentioned that one can similarly obtain an expression for ${L}_{4}^{(1)}$ which has been omitted here due to its lengthy form.

The TL-skewness ${\tau }_{3}^{(1,0)}$ and TL-kurtosis ${\tau }_{4}^{(1,0)}$ of Sushila distribution can be calculated by solving

$${\tau }_{3}^{(1,0)}=\frac{ {L}_{3}^{(1)}}{{L}_{2}^{(1)} }\mathrm{and }{\tau }_{4}^{(1,0)}=\frac{ {L}_{4}^{(1)}}{{L}_{2}^{(1)} }, \mathrm{respectively}.$$

3.4 Sample TL-Moments and TL-Moment Estimators

The TL-moments can be estimated from a sample as linear combination of order statistics. Elamir and Seheult [7] presented the following estimator for TL-moments:

$${l}_{r}^{({t}_{1},{t}_{2})}=\frac{1}{r\left(\genfrac{}{}{0pt}{}{n}{r+{t}_{1}+{t}_{2}}\right)}\sum_{i={t}_{1}+1}^{n-{t}_{2}}\sum_{k=0}^{r-1}{(-1)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)\left(\genfrac{}{}{0pt}{}{i-1}{r+{t}_{1}-k-1}\right)\left(\genfrac{}{}{0pt}{}{n-i}{k+{t}_{2}}\right){x}_{i:n}. $$

(41)

If we take ${t}_{1}=1, {t}_{2}=0$ in (41), we get ${l}_{r}^{(1,0)}\equiv {l}_{r}^{\left(1\right)}:$

$${l}_{r}^{(1)} =\frac{1}{r\left(\genfrac{}{}{0pt}{}{n}{r+1}\right)}\sum_{i=2}^{n}\sum_{k=0}^{r-1}{(-1)}^{k}\left(\genfrac{}{}{0pt}{}{r-1}{k}\right)\left(\genfrac{}{}{0pt}{}{i-1}{r-k}\right)\left(\genfrac{}{}{0pt}{}{n-i}{k}\right){x}_{i:n} .$$

(42)

From Eq. (42), for $r=$ 1, 2, we get the sample TL-moments ${l}_{1}^{(1)} \; \mathrm{and} \; {l}_{2}^{(1)}$. Equating sample.

TL-moments with the population TL-moments ${L}_{1}^{(1)} \; \mathrm{and} \; {L}_{2}^{(1)}$ as given by Eqs. (38) and (39), respectively, we get

$${l}_{1}^{(1)}= \frac{2}{n(n-1)}\sum_{i=2}^{n}(i-1){x}_{i:n}=\frac{\lambda }{4\alpha {\left(\alpha +1\right)}^{2}}\left(6{\alpha }^{2}+18\alpha +11\right),$$

(43)

and

$${l}_{2}^{(1)}= \frac{3}{2n(n-1)(n-2)}\sum_{i=2}^{n}\left(i-1\right)\left[\left(i-2\right)-2(n-i)\right]{x}_{i:n}=\frac{\lambda }{36\alpha {\left(\alpha +1\right)}^{3}}\left(18{\alpha }^{3}+72{\alpha }^{2}+75\alpha +25\right).$$

(44)

By solving (43) and (44) simultaneously, using program in R, we have obtained the TL-moment estimators (${\widehat{\mathrm{\alpha }}}_{\mathrm{TLM}} \; \mathrm{and} \; {\widehat{\lambda }}_{\mathrm{TLM}}$) of the parameters α and λ of Sushila distribution, which are calculated and presented in columns 3rd and 7th in Tables 6, 7, 8 and 9, for different values of α and λ.

4 Method of Moments

Suppose $X$ is a continuous random variable with probability density function (pdf) ${f}_{\theta }(x,{\theta }_{1},{\theta }_{2},\ldots .{\theta }_{k})$ characterized by $k$ unknown parameters. Let ${X}_{1}, {X}_{2},\ldots ,{X}_{n}$ be a random sample of size $n$ from $f(x)$.

Defining the first $k$ sample moments about origin as

$${m}_{r}^{\prime}= \frac{1}{n} \sum_{i=1}^{n}{X}_{i}^{r} , r=1,2,3,\ldots ,k .$$

The first k population moments about origin are given by

$${\mu }_{r}^{\prime}=E\left({X}^{r}\right), r=1,2,3,\ldots ,k ,$$

which are in general functions of $k$ unknown parameters.

Equating the sample moments and the population moments yield k simultaneous equations in k unknowns, i.e.,

$${\mu }_{r}^{\prime}= {m}_{r}^{\prime} , r= 1,2,3,\ldots , k.$$

The solutions to the above equations denoted by ${\widehat{\theta }}_{1}$, ${\widehat{\theta }}_{2},$ … ${\widehat{,\theta }}_{k}$ yield the moment estimators of ${\theta }_{1},{\theta }_{2},\ldots ,{\theta }_{k}$.

The first two population moments of Sushila distribution are given, respectively, as

$${\mu }_{1}^{\prime}= \frac{\lambda (\alpha +2)}{\alpha (\alpha +1)} , \mathrm{and}$$

(45)

$${\mu }_{2}^{\prime}= \frac{2{\lambda }^{2}(\alpha +3)}{{\alpha }^{2}(\alpha +1)}$$

(46)

For n observations ${x}_{1}{,x}_{2},\ldots ,{x}_{n}$ from Sushila distribution the first two sample moments are obtained as

$${m}_{1}^{\prime}=\overline{x } , \mathrm{and}$$

(47)

$${m}_{2}^{\prime}=\frac{1}{n}\sum_{i=1}^{n}{X}_{i}^{2} .$$

(48)

Equating the sample moments as obtained in Eqs. (47) and (48), with the population moments as given by Eqs. (45) and (46), we have

$$\overline{x }=\frac{\lambda (\alpha +2)}{\alpha (\alpha +1)} , \mathrm{and}$$

(49)

$$\frac{1}{n}\sum_{i=1}^{n}{X}_{i}^{2}=\frac{2{\lambda }^{2}(\alpha +3)}{{\alpha }^{2}(\alpha +1)} .$$

(50)

By solving (49) and (50) simultaneously, using program in R, we have obtained the method of moments estimators (${\widehat{\mathrm{\alpha }}}_{\mathrm{MM}} \; \mathrm{and} \; {\widehat{\lambda }}_{\mathrm{MM}}$) of the parameters α and λ of Sushila distribution, which are calculated and presented in columns 4th and 8th in Tables 6, 7, 8 and 9, for different values of α and λ.

5 Maximum Likelihood Estimator

For n observations${x}_{1}$, ${x}_{2}$, …, ${x}_{n}$ from Sushila distribution, the likelihood function is given by:

$$L\left(\alpha ,\lambda \right)=\prod_{i=1}^{n}\frac{{\alpha }^{2}}{\lambda \left(1+\alpha \right)}\left(1+\frac{{x}_{i}}{\lambda }\right){e}^{-\frac{\alpha }{\lambda }{x}_{i}} .$$

Consequently, the log likelihood function is

$$ log\left(L\left(\alpha ,\lambda \right)\right)=2nlog\left(\alpha \right)-nlog\lambda -nlog\left(1+\alpha \right)+\sum_{i=1}^{n}\mathit{log}\left(1+\frac{{x}_{i}}{\lambda }\right)-\frac{\alpha }{\lambda }\sum_{i=1}^{n}{x}_{i}.$$

(51)

Differentiating (51) with respect to α and λ, and equating to zero, we get

$$\frac{\partial \mathrm{log}(L\left(\alpha ,\lambda \right))}{\partial \alpha }=\frac{2n}{\alpha }-\frac{n}{1+\alpha }-\frac{n\overline{x}}{\lambda }=0,$$

(52)

$$\frac{\partial \mathrm{log}(L\left(\alpha ,\lambda \right))}{\partial \lambda } =-\frac{n}{\lambda }-\frac{1}{\lambda }\sum_{i=1}^{n}\frac{{x}_{i}}{{x}_{i}+\lambda }+\frac{n\alpha \overline{x}}{{\lambda }^{2}} =0.$$

(53)

It may be mentioned that Eq. (52) yields $\overline{x }= \frac{\lambda (2+\alpha )}{\alpha (1+\alpha )}$, which is the population mean of Sushila distribution. But the two Eqs. (52) and (53) cannot be solved simultaneously to get the MLEs of α and λ. In this situation one may use the Fisher’s scoring method to get the MLEs of α and λ (cf. [21]). However, we have used the program in R for solving Eqs. (52) and (53) to obtain the MLEs (${\widehat{\mathrm{\alpha }}}_{\mathrm{MLE}} \; \mathrm{and} \;{\widehat{\lambda }}_{\mathrm{MLE}}$) of the parameters α and λ of Sushila distribution, which are calculated and presented in columns 5th and 9th in Tables 6, 7, 8 and 9, for different values of α and λ.

5.1 The Maximum Likelihood Estimators of ${\varvec{R}}\left({\varvec{t}}\right)$ and ${\varvec{P}}$

The reliability function $R\left(t\right)$ is defined as the probability of failure-free operation until time t. Thus if the random variable X denotes the lifetime of an item, then $R\left(t\right)=Pr ( X>t)$. Another measure of reliability under stress-strength set-up is the probability $P=Pr(X>Y)$, which is a measure of component reliability when it is subjected to random stress Y and has strength X.

It has many applications in engineering, industrial system, economics and medical sciences. For more details and applications, see Kotz et al. [12]. Much work has been done on the problem of estimating $R\left(t\right)$ and P by many authors such as Raqab and Kundu [16], Raqab et al. [17], Kundu and Raqab [13], Gupta et al. [9], Rao et al. [15], etc.

The reliability function $R(t)$ for any distribution is given as

$$R\left(t\right)=\underset{t}{\overset{\infty }{\int }}f\left(x\right)dx .$$

(54)

Substituting the value of $f(x)$ from (1), we get the reliability function of Sushila distribution as

$$R\left(t\right)=\left(1+\frac{\alpha t}{\lambda (1+\alpha )}\right) {e}^{-\frac{\alpha }{\lambda }t}$$

(55)

Let X and Y be two random variables as part of Sushila distribution with parameters $({\alpha }_{1} , {\lambda }_{1} )$ and (${\alpha }_{2} , {\lambda }_{2}$), respectively. Suppose ${X}_{1 }, {X}_{2},\ldots ,{X}_{n}$ and ${Y}_{1},{Y}_{2},\ldots ,{Y}_{n}$ are two independent samples from X and Y, respectively. The strength and the stress are assumed to be independent. Based on these assumptions, we find the reliability under stress-strength set-up to be

$$P= Pr\left(X>Y\right)= \underset{y=0}{\overset{\infty }{\int }}\underset{x=y}{\overset{\infty }{\int }}{f}_{1}( x: {\alpha }_{1} , {\lambda }_{1}){f}_{2}( y: {\alpha }_{2} , {\lambda }_{2})dx dy$$

$$= \underset{0}{\overset{\infty }{\int }}{F}_{2}\left( x: {\alpha }_{2} , {\lambda }_{2}\right){f}_{1}\left( x: {\alpha }_{1} , {\lambda }_{1}\right)dx.$$

(56)

Putting the values of $f(x)$ and $F(x)$ from (1) and (2) in (56), and simplifying, we obtain

$$P=1-\frac{{\lambda }_{2}{{\alpha }_{1}}^{2} \left[{{\alpha }_{2}}^{3}{{\lambda }_{1}}^{2}+ {{\alpha }_{2}}^{2}\left({{\lambda }_{1}}^{2}+2{\alpha }_{1}{\lambda }_{1} {\lambda }_{2}+{\lambda }_{1} {\lambda }_{2}+{\lambda }_{1}\right)+{\alpha }_{2}\left({{\alpha }_{1}}^{2}{{\lambda }_{2}}^{2}+{\alpha }_{1}\left({{\lambda }_{2}}^{2}+2{\lambda }_{1} {\lambda }_{2}+{\lambda }_{2}\right)+3{\lambda }_{1} {\lambda }_{2}\right)+{\alpha }_{1}{{\lambda }_{2}}^{2}\left({\alpha }_{1}+1\right)\right] }{\left(1+{\alpha }_{1}\right)\left(1+{\alpha }_{2}\right){\left({\alpha }_{1}{\lambda }_{2}+{\alpha }_{2}{\lambda }_{1}\right)}^{3}}.$$

(57)

By the invariance property of the MLE, the MLE of $R\left(t\right)$ is given by

$$\widehat{R}\left(t\right)= \left(1+\frac{\widehat{\alpha }t}{\widehat{\lambda }(1+\widehat{\alpha })}\right) {e}^{-\frac{\widehat{\alpha }}{\widehat{\lambda }}t},$$

(58)

where $\widehat{\alpha }$ and $\widehat{\lambda }$ are the MLE’s of α and λ, respectively.

The MLE of P can be obtained by replacing ${\alpha }_{1}, {\alpha }_{2},$ ${\lambda }_{1}$ and ${\lambda }_{2}$ by their respective MLEs in (57).

5.2 Numerical illustration

The following two samples of size 50 each, have been generated, one from each of the X and Y populations with parameters (${\alpha }_{1}$ = 1, ${\lambda }_{1}$ = 1) and (${\alpha }_{2}$ = 1.2, ${\lambda }_{2}$ = 0.8), respectively. For simplicity, these samples have been arranged in increasing order of magnitude.

SAMPLE 1 (from X population with ${\boldsymbol{\alpha }}_{1}$ = 1, ${{\varvec{\lambda}}}_{1}$ = 1).

0.01057119, 0.05147864, 0.06885357, 0.09171968, 0.14414112, 0.14671290, 0.15447993,
0.16644394, 0.17042160, 0.24709920, 0.28271315, 0.52224349, 0.59598601, 0.59851715,
0.65542551, 0.66723839, 0.74504209, 0.75123431, 0.79042277, 0.96853265, 0.97028999,
1.02032867, 1.07222429, 1.11045944, 1.18419957, 1.46491615, 1.55315019, 1.62745865,
1.65891723, 1.71916719, 1.74750811, 1.91878133, 2.01547597, 2.18346283, 2.19104768,
2.21366160, 2.28856621, 2.35461178, 2.53634355, 2.61765239, 2.66514137, 2.79300971,
2.92873765, 3.02959314, 3.13195261, 3.35918440, 3.63031498, 3.64321909, 3.72483437,
5.26073134

SAMPLE 2 (from Y population with ${\boldsymbol{\alpha }}_{2}$ = 1.2, ${{\varvec{\lambda}}}_{2}$ = 0.8).

0.008060041, 0.027557300, 0.054899743, 0.060554533, 0.100659360, 0.138896234, 0.157492622,
0.192150945, 0.198538135, 0.355504366, 0.387270098, 0.410108480, 0.411550262, 0.427598532,
0.454680266, 0.512139070, 0.666895602, 0.670973554, 0.773955898, 0.853672445, 0.956721984,
0.976265420, 1.017888021, 1.036076410, 1.156120042, 1.202503052, 1.218480323, 1.257862460,
1.269335361, 1.365347999, 1.375775709, 1.413147579, 1.492950530, 1.499182716, 1.509740345,
1.554593405, 1.596011687, 1.618487215, 1.741430326, 1.786273292, 1.848323182, 1.864724509,
1.875999601, 2.082839850, 2.621169405, 2.945736835, 3.039685190, 3.753240192, 4.083521702,
5.906188950

Utilizing the above two randomly generated samples, using a program in R, we have calculated the MLEs of ${\alpha }_{1}, {\lambda }_{1},{ \alpha }_{2} \; \mathrm{and } \; {\lambda }_{2}$.

For sample 1, ${\alpha }_{1}$ = 1 and ${\lambda }_{1}$= 1, and the corresponding MLEs are ${({\widehat{\alpha }}_{1})}_{MLE}$= 1.1067 and ${({\widehat{\lambda }}_{1})}_{MLE}$= 1.1624.

For sample 2, ${\alpha }_{2}$ = 1.2 and ${\lambda }_{2}$= 0.8, and the corresponding MLEs are ${({\widehat{\alpha }}_{2})}_{MLE}$= 1.1433 and ${({\widehat{\lambda }}_{2})}_{MLE}$ = 0.9968. Utilizing the values of these estimators, we have found out the MLE of $R\left(t\right)$(using (58)), for Sample 1 and Sample 2, which are presented in Tables 3 and 4, respectively.

Table 3 MLE of $R\left(t\right)$ for Sample 1

Table 4 MLE of $R\left(t\right)$ for Sample 2

(The values of t have been taken in accordance to the samples generated.)

Using (57) the value of P = Pr(X > Y) and its MLE ${\widehat{P}}_{MLE}$, for the above two samples from populations $X \mathrm{and} Y$, are obtained in Table 5.

Table 5 MLE of the parameters and P

6 Simulation Study

By generating samples of size 10, 20, 50, 100, 200, 300 and 500 with 1000 replications and applying the program in R, the L-Moment, TL-Moment, method of moments (MM) estimators and MLEs of the unknown parameters α and λ along with their mean square errors (MSEs) are computed and presented in the following Tables 6, 7, 8 and 9.

Table 6 L-moment (LM) estimators, TL-moment (TLM) estimators, MLEs and method of moments (MM) estimators of α and λ along with their Mean square error (MSE) of Sushila distribution for α = 1 and λ = 0.5

Table 7 L-moment (LM) estimators, TL-moment (TLM) estimators, MLEs and method of moments (MM) estimators of α and λ along with their Mean square error (MSE) of Sushila distribution for α = 1 and λ = 1

Table 8 L-moment (LM) estimators, TL-moment (TLM) estimators, MLEs and method of moments (MM) estimators of α and λ along with their Mean square error (MSE) of Sushila distribution for α = 0.5 and λ = 1

Table 9 L-moment (LM) estimators, TL-Moment (TLM) estimators, MLEs and method of moments (MM) estimators of α and λ along with their Mean square error (MSE) of Sushila distribution for α = 1.2 and λ = 0.8

From Tables 6, 7, 8 and 9, we observe that

• The values of MSEs for ${\widehat{\alpha }}_{LM}$, ${\widehat{\alpha }}_{TLM}$,${\widehat{\alpha }}_{MM}$ and ${\widehat{\mathrm{\alpha }}}_{\mathrm{MLE}}$ decrease with the increase in the value of n.

• The values of MSEs for ${\widehat{\lambda }}_{LM}$, ${\widehat{\lambda }}_{TLM}$,${\widehat{\lambda }}_{MM}$ and ${\widehat{\uplambda }}_{\mathrm{MLE}}$ decrease with the increase in the value of n.

• The values of MSEs for both ${\widehat{\alpha }}_{TLM}$ and ${\widehat{\lambda }}_{TLM}$ are smaller than the corresponding values for other estimates for all sample sizes. Thus, we may suggest that ${\widehat{\alpha }}_{TLM}$ and ${\widehat{\lambda }}_{TLM}$ give better estimators of α and λ, as compared to other methods of estimation.

7 Conclusion

In this paper, we have obtained the exact expression and recurrence relations for single moments of order statistics arising from Sushila distribution. We have considered the problem of estimation of parameters α and λ of Sushila distribution by four different methods, namely L-moments, TL-moments, method of Moments and Maximum Likelihood estimation.

By simulation we made a comparison between the L-moment estimators, TL-moment estimators, Method of Moments estimators and MLEs for both α and λ. It has been observed that in all the four methods of estimation, the mean square error, for both the estimators $\widehat{\alpha }$ and $\widehat{\lambda }$, decreases as sample size increases. Also, the TL-moment estimators of both α and λ have mean square errors that are less than the corresponding mean square errors of the other estimators, as observed in Tables 6, 7, 8 and 9. Hence, we suggest that ${\widehat{\mathrm{\alpha }}}_{\mathrm{TLM}}$ and ${\widehat{\uplambda }}_{\mathrm{TLM}}$ may be regarded as the best estimators of α and λ, among all the four estimators.