1 Introduction

In several situations, when we try to gather information on the environmental inquiry, several types of issues come up. Due to the lack of sample selection, it might be challenging in the majority of cases to acquire a simple random sample (SRS). It is likewise challenging to make free decisions about where to gather observations following a predetermined plan. An effective foundation for estimating the parameters of environmental variables may be found in ranked set sampling (RSS). Under extremely certain conditions, such as when sample units can be readily and cheaply obtained and ranked among themselves, but it is relatively expensive to measure them properly, RSS can offer an observational economy. Ranking may be done visually about the research variable or by using any simple, economical way. For instance, ranking a small group of trees according to their heights visually is simple if the goal is to estimate the average height of trees. The RSS approach was initially proposed by [1] for estimating pasture and forage yields. The RSS approach entails selecting m sets of size m each at random from a population and visually ranking the units in each set or using some other low-cost method. The unit with the lowest ranking among the first m units is chosen for actual quantization. The unit ranked second lowest among the second batch of m units is picked for actual quantification. The procedure is repeated up until the mth set’s largest-ranked unit is selected for actual quantification. The one-cycle RSS of m samples of size m is represented as follows:

$$\begin{aligned} \hspace{-1cm} \begin{array}{*{20}{c}} {1:} \\ {2:} \\ \vdots \\ {m:} \end{array}\left( \begin{aligned} \boxed {{X_{(1:1)1}}}\quad {X_{(2:1)1}}\quad \ldots \quad {X_{(m:1)1}} \\ {X_{(1:2)2}}\quad \boxed {{X_{(2:2)2}}}\quad \ldots \quad {X_{(m:2)2}} \\ \vdots \quad \;\;\;\quad \vdots \quad \quad \; \ddots \quad \;\; \vdots \\ {X_{(1:m)m}}\quad {X_{(2:m)m}}\quad .\quad \;\,\boxed {{X_{(m:m)m}}} \\ \end{aligned} \right) \begin{array}{*{20}{c}} \rightarrow \\ \rightarrow \\ \rightarrow \\ \rightarrow \end{array}\begin{array}{*{20}{c}} {{Y_1} = } \\ {{Y_2} = } \\ {} \\ {{Y_m} = } \end{array}\begin{array}{*{20}{c}} {{X_{(1:1)1}}} \\ {{X_{(2:2)2}}} \\ \vdots \\ {{X_{(m:m)m}}} \end{array}, \end{aligned}$$

where \({X_{\left( {i:m} \right) j}}\) represents the \({i^{th}}\) order statistic from the \({j^{th}}\) SRS of size m. The observed sample \({\text {Y }} = \left( {{Y_1},{Y_2},\ldots ,{Y_m}} \right)\) is called a one-cycle RSS of size m. In a sample of size m, it marginally, \({Y_{\left( i \right) }}\) has the same distribution as the probability density function (PDF) given below (see [2])

$$\begin{aligned} {f_{(i)}}(y) = \frac{{m!}}{{(i - 1)!(m - i)!}}\,\,{\left[ {F(y)} \right] ^{i - 1}}f(y){\left[ {1 - F(y)} \right] ^{m - i}},\, - \infty< y < \infty . \end{aligned}$$

The process of determining precisely how reliable a system or a component is called reliability estimate. Reliability estimate is essential in today’s technologically advanced environment to make sure systems function as intended and reduce failure risk. It entails gathering performance data from the system, evaluating the data, and forecasting future performance. Recent studies in this estimating technique can be found in [3,4,5,6]. In some situations, the life of a component with a random strength X and a random stress Y is described by the stress strength (SS) model. This idea emerged in the context of the traditional SS reliability when the person is interested in predicting the probability \(P\left( {Y < X} \right)\) which can be seen as the probability that a component would fail when applied stress Y is larger than its strength (see [7]). This model has several uses in a variety of fields, especially in engineering, such as building structures, the aging of concrete pressure vessels, and the deterioration of rocket engines. There are several more significant studies in this field as well, such as those by Refs. [8,9,10,11,12] among others. Several studies in recent years have taken into account SS model inferential statistics using the RSS method. The unbiased estimator for R where X and Y are from an exponential distribution was discovered by Sengupta and Mukhuti [13]. It was applied to the Weibull distribution, respectively, by [14]. More recent studies can be found in [15,16,17,18,19,20,21,22,23,24,25].

The multi-stressstrength systems model, which is also an essential SS model in which component fails when exposed to extreme lower and upper working environments, that is, \(R = P\left( {Y< X < Z} \right)\), where Y and Z are the component stresses (lower and upper), and X is the strength of the component, is given much fewer spotlights. Reference [26] was the ones who initially presented the primary concept of this methodology. For instance, many gadgets are incapable of operating in both extremely hot and low temperatures. Similar to this, a person’s systolic and diastolic blood pressure has two limitations, and it should stay within these ranges. In a related manner, numerous devices are unworkable in two extremes of stress.

In the literature, the estimate of \(R = P\left( {{X_1}< Y < {X_2}} \right)\) where \({X_1},Y,\) and \({X_2}\) are exponentially distributed was covered by Ref. [27]. Singh [28] explored the uniform minimum variance unbiased estimators (UMVUEs) and the maximum likelihood estimators (MLEs) of \(R = P\left( {X< Y < Z} \right)\), where X, Y,  and Z are independent random variables that have a normal distribution. The MLE and UMVUE of R were given by Ivshin [29] when X, Y,  and Z are either random variables that are exponential or uniform. Guangming et al. [30] constructed a statistical inference for R under the assumption that the three samples were independent. Reference [31] has offered an estimation of R for independent Weibull distributions with k outliers. Recently, studies on R in complete samples were presented by Hameed et al. [32] for inverted Kumaraswamy distribution (IKwD). References [33, 34] investigated several strategies for estimating R for the inverse Rayleigh distribution. When data are observed from independent Kumaraswamy distributions, Ref. [35] provided classical and Bayesian estimates of R. The Bayesian and non-Bayesian estimates of R from the exponentiated exponential distribution were supplied by Yousef et al. [36] based on generalized progressive hybrid censoring.

Only one recent work has examined the estimation issue of \(R = P(W<X<Z)\) under RSS methodology in the literature, assuming that both stresses and strength random variables follow generalized inverse exponential distributions [37]. Here, the primary goal is to handle the the estimation issue of \(R = P(W<X<Z)\) in light of RSS method. This concentration’s idea came from the variety of areas that apply the RSS strategy. Additionally, compared to the SRS design, the RSS design provides more efficient estimators for a given sample size. Assume the stresses and strength random variables follow the IKwD, due to the significance of this distribution and its wide range of applications. In addition, this study uses the maximum product of the spacing (MPS) estimation approach as an additional estimation technique in comparison to the work previously offered by Hassan et al. [37]. Consequently, the following is a summary of this effort:

  • The MLE and MPS estimator (MPSE) of \(R = P(W<X<Z)\) are derived under four situations for RSS and SRS methods.

  • The MLE and MPSE of \(R = P(W<X<Z)\) are generated when the stresses(W, Z), and strength (X) have the same sampling design (RSS/RSS) as done in the first and second scenarios.

  • The MLE and MPSE of \(R = P(W<X<Z)\) are determined when the observed samples of the stresses (W, Z) are taken from RSS, whereas the observed samples of strength (X) are taken from SRS in the third scenario.

  • In the last case, the reliability estimators are produced when the observed samples of the stresses are gathered from SRS, whereas observed samples of the strength are taken from RSS.

  • Extensive simulations were done to compare the two approaches, and the dataset was assessed for better clarification.

The following is an outline for this article. The model description and its reliability expression are included in Sect. 2. When both stresses and strength distributions have the same sampling design, Sects. 3 and 4 deduce the MLE and MPSE of R. As demonstrated in Sect. 5, the estimator of R is determined when stresses have the SRS and strength has the RSS using both estimation methods. The estimator of R is deduced when stresses have the RSS and strength has the SRS using the proposed estimation methods, as documented in Sect. 6. Sections 7 and 8 provide, respectively, techniques for simulating and analyzing real data. In Sect. 9 we conclude the paper.

2 Description of the Model and Its Reliability

In this section, a description of the model is explained and an expression of \(R = \,P[W< X < Z]\) is obtained, where independent random variables X, W,  and Z adhere to the IKwD.

The inverse of the probability distributions is useful for examining further characteristics of the phenomena. Inverted distributions have been demonstrated to be useful in research based on econometrics, biological and engineering sciences, survey sampling, medical applications, and life testing issues. Recently, Abd AL-Fattah et al. [38] provided the IKwD for a random variable \(X = (1/Y) - 1\), where the random Y has a Kumaraswamy distribution. The PDF, survival function (SF) and hazard rate function (HRF) of the IKwD are, represented, by:

$$\begin{aligned} f(x)= & {} \lambda {\rho _1}{(1 + x)^{ - \lambda - 1}}{\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] ^{{\rho _1} - 1}};\,\,\,\,\,\,\,\,\,\,\,x,{\rho _1},\lambda > 0,\,\,\, \end{aligned}$$
(1)
$$\begin{aligned} {\bar{F}}(x)= & {} 1 - {\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] ^{{\rho _1}}};\,\,\,\,\,\,\,\,\,\,\,x,{\rho _1},\lambda > 0,\, \end{aligned}$$
(2)

and

$$\begin{aligned} h(x) = \frac{\lambda {\rho _1}{(1 + x)^{ - \lambda - 1}}{\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] ^{{\rho _1} - 1}}}{1 - {\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] ^{{\rho _1}}}};\,\,\,\,\,\,\,\,\,\,\,x,{\rho _1},\lambda > 0,\,\,\, \end{aligned}$$
(3)

where, \(\lambda\) and \({\rho _1}\) are the shape parameters. The PDF (1) comprises some distributions for some choices of \(\lambda\) and \({\rho _1}\). At \({\rho _1} = 1,\) the PDF (1) provides the Lomax distribution; at \(\lambda = 1,\) the PDF (1) gives beta Type II distribution. Also, at \(\lambda = {\rho _1} = 1,\) the PDF (1) reduces to log-logistic distribution. The PDF (1) gives the inverse Weibull distribution when \({\rho _1} \rightarrow \infty ,\) and the generalized exponential distribution when \(\lambda \rightarrow \infty .\) Figures 1 and 2 display the PDF and HRF of the IKwD for some choices of parameters. From Figs. 1 and 2, we can note that the PDF of the IKwD can be unimodal, decreasing and right skewed, but the HRF can be decreasing, reversed J-shaped and up-side-down.

Fig. 1
figure 1

Plots of the PDF of the IKwD

Full size image
Fig. 2
figure 2

Plots of the HRF of the IKwD

Full size image

The IKwD yields beneficial estimates of rare occurrences happening in the right tail of the distribution when compared to other distributions, making it useful for long-term reliability predictions [39]. Compared to other commonly used distributions, the IKwD has a longer right tail, which has a beneficial impact on the distribution’s capacity to match the infrequent occurrences that occur in the right tail, or outlier data in the right tail. In place of the widely used Weibull distribution, the IKwD was employed for modelling wind speed data [40]. Using dual generalized order statistics, Ref. [41] determined the shape parameters, SF, and hazard function of IKwD. The Bayesian estimation of mixed IKwD with application to 56 observations related to the burning velocity of different chemical materials was examined by [42]. Reference [43] examined several estimate techniques for the IKwD parameters using RSS and applied them to the waiting periods between 65 successive eruptions of the Kiama Blowhole. For more studies of the IKwD in life testing experiment [44, 45].

Expression of \(R = P[W< X < Z],\) is derived, where the strength \(X\sim\)IKwD\((\lambda ,{\rho _1})\) and the two stress random variables \(W\sim\)IKwD\((\lambda ,{\rho _2})\) and \(Z\sim\)IKwD\((\lambda ,{\rho _3})\) are independent. Reference [28] argued that the SS model’s reliability \(R = \,P[W< X < Z],\) formula has the following structure:

$$\begin{aligned} R = P[W< X < Z] = \int _{ - \infty }^\infty {{G_W}\left( x \right) {{{\bar{H}}}_Z}\left( x \right) d{F_X}\left( x \right) ,} \end{aligned}$$
(4)

where \({{\bar{H}}_Z}\left( x \right)\) is the SF of stress Z at x, and \({G_W}\left( x \right)\) is the cumulative distribution function of W at x. Consequently, based on (4), we obtain R as follows:

$$\begin{aligned} \begin{aligned} R&= \,P[W< X < Z] = \lambda {\rho _1}\int _0^\infty {{{\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] }^{{\rho _2}}}{{(1 + x)}^{ - \lambda - 1}}} \\&\quad \times \left[ {\;1 - {{\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] }^{{\rho _3}}}} \right] {\left[ {1 - {{\left( {1 + x} \right) }^{ - \lambda }}} \right] ^{{\rho _1} - 1}}dx \\&= \frac{{{\rho _1}}}{{\left( {{\rho _1} + {\rho _2}} \right) }} - \frac{{{\rho _1}}}{{\left( {{\rho _1} + {\rho _2} + {\rho _3}} \right) }} = \frac{{{\rho _1}{\rho _3}}}{{\left( {{\rho _1} + {\rho _2}} \right) \left( {{\rho _1} + {\rho _2} + {\rho _3}} \right) }}. \\ \end{aligned} \end{aligned}$$
(5)

Note that formula (5), depends on the parameters \({\rho _1},{\rho _2}\) and \({\rho _3}\).

3 Estimator of \({R_1} = \,P[{W_{SRS}}< {X_{SRS}} < {Z_{SRS}}]\)

This section discusses, the MLE and MPSE of \({R_1},\) designed respectively by \({{\hat{R}}_1},\) and \({{\tilde{R}}_1},\) when the observed samples for both stresses and strength are taken from SRS.

3.1 MLE of \({R_1}\)

Let \({X_1},{X_2},\ldots ,{X_{m_1^*}}\), \({W_1},{W_2},\ldots ,{W_{m_2^*}},\) and \({Z_1},{Z_2},\ldots ,{Z_{m_3^*}},\) are independent IKwD with parameters \((\lambda ,{\rho _{1}}),\) \((\lambda ,{\rho _2}),\) and \((\lambda ,{\rho _3}),\) respectively, under SRS. First, we acquire the MLE of \({\rho _1},{\rho _2},{\rho _3}\) and \(\lambda\), then use that information to derive the MLE of \({R_1}\) following the invariance property. The likelihood function of SRS is

$$\begin{aligned} {L_1}(\Psi ) = \prod \limits _{{j_1} = 1}^{m_1^ * } {f({x_{{j_1}}},\lambda ,{\rho _1})\prod \limits _{{j_2} = 1}^{m_2^* } {f({w_{{j_2}}},\lambda ,{\rho _2})\prod \limits _{{j_3} = 1}^{m_3^* } {f({z_{{j_3}}},\lambda ,{\rho _3})} } }, \end{aligned}$$

where \(\Psi \equiv ({\rho _1},{\rho _2},{\rho _3},\lambda ).\) The log-likelihood function, say \({\ell _1}(\Psi ),\) is as follows:

$$\begin{aligned} \begin{aligned} {\ell _1}(\Psi )&= m_1^*\log {\rho _1} + m_2^*\log {\rho _2} + m_3^*\log {\rho _3} + (m_1^* + m_2^* + m_3^*)\log \lambda \\&\quad - (\lambda + 1)A({x_{{j_1}}},{w_{{j_2}}},{z_{{j_3}}}) + ({\rho _1} - 1)\sum \limits _{{j_1} = 1}^{m_1^*} {\log {H_1}({x_{{j_1}}},\lambda )} \\&\quad + ({\rho _2} - 1)\sum \limits _{{j_2} = 1}^{m_2^*} {\log {H_2}({w_{{j_2}}},\lambda ) + } ({\rho _3} - 1)\sum \limits _{{j_3} = 1}^{m_3^*} {\log {H_3}({z_{{j_3}}},\lambda )}, \\ \end{aligned} \end{aligned}$$
(6)

where, \(A({x_{{j_1}}},{w_{{j_2}}},{z_{{j_3}}}) = \sum \nolimits _{{j_1} = 1}^{m_1^*} {\log } \,(1 + {x_{{j_1}}}) + \sum \nolimits _{{j_2} = 1}^{m_2^*} {\log } \,(1 + {w_{{j_2}}}) + \sum \nolimits _{{j_3} = 1}^{m_3^*} {\log } \,(1 + {z_{{j_3}}}),\) \({H_1}({x_{{j_1}}},\lambda ) = \left[ {1 - {{\left( {1 + {x_{{j_1}}}} \right) }^{ - \lambda }}} \right] ,\) \({H_2}({w_{{j_2}}},\lambda ) = \left[ {1 - {{\left( {1 + {w_{{j_2}}}} \right) }^{ - \lambda }}} \right] ,\) and \({H_3}({z_{{j_3}}},\lambda ) = \left[ {1 - {{\left( {1 + {z_{{j_3}}}} \right) }^{ - \lambda }}} \right] .\) The equations following are produced by differentiating (6) concerning the population parameters.

$$\begin{aligned} \frac{{\partial {\ell _1}(\Psi )}}{{\partial {\rho _1}}}= & {} \frac{{m_1^*}}{{{\rho _1}}} + \sum \limits _{{j_1} = 1}^{m_1^*} {\log {H_1}({x_{{j_1}}},\lambda )},\nonumber \\ \frac{{\partial {\ell _1}(\Psi )}}{{\partial {\rho _2}}}= & {} \frac{{m_2^*}}{{{\rho _2}}} + \sum \limits _{{j_2} = 1}^{m_2^*} {\log {H_2}({w_{{j_2}}},\lambda )},\nonumber \\ \frac{{\partial {\ell _1}(\Psi )}}{{\partial {\rho _3}}}\,\,\,{} & {} = \frac{m_3^*}{{{\rho _3}}} + \sum \limits _{{j_3} = 1}^{m_3^*} {\log {H_3}({z_{{j_3}}},\lambda ),} \end{aligned}$$
(7)
$$\begin{aligned} \frac{{\partial {\ell _1}(\Psi )}}{{\partial \lambda }}= & {} \frac{{{m_1^*}+ {m_2^*}+ {m_3^*}}}{\lambda } - A({x_{{j_1}}},{w_{{j_2}}},{z_{{j_3}}}) \nonumber \\{} & {} + \sum \limits _{{j_1} = 1}^{{m_1^*}} {\frac{{({\rho _1} - 1)\left( {{{H'}_1}({x_{{j_1}}},\lambda )} \right) }}{{{H_1}({x_{{j_1}}},\lambda )}}} + \sum \limits _{{j_2} = 1}^{{m_2^*}} {\frac{{({\rho _2} - 1)\left( {{{H'}_2}({w_{{j_2}}},\lambda )} \right) }}{{{H_2}({w_{{j_2}}},\lambda )}}} \nonumber \\{} & {} + \sum \limits _{{j_3} = 1}^{{m_3^*}} {\frac{{({\rho _3} - 1)\left( {{{H'}_3}({z_{{j_3}}},\lambda )} \right) }}{{{H_3}({z_{{j_3}}},\lambda )}}} , \end{aligned}$$
(8)

where, \(\frac{\partial }{{\partial \lambda }}{H_k}({\upsilon _{{j_k}}},\lambda ) = {H'_k}({\upsilon _{{j_k}}},\lambda ) = {\left( {1 + {\upsilon _{{j_k}}}} \right) ^{ - \lambda }}\log \left( {1 + {\upsilon _{{j_k}}}} \right) ,{\upsilon _{{j_k}}} \equiv \left( {{x_{{j_1}}},{w_{{j_2}}},{z_{{j_3}}}} \right) ,k = 1,2,3.\) Set Eq. (7) with zero gives the MLEs of \({\rho _1},{\rho _2}\) and \({\rho _3},\) say \({{\hat{\rho }} _1},\,\,{{\hat{\rho }} _2}\) and \({{\hat{\rho }} _3},\) as a function of \(\lambda\) as seen below:

$$\begin{aligned} {{{\hat{\rho }} }_1}(\lambda ) = \frac{{ - m_1^*}}{{\sum \nolimits _{{j_1} = 1}^{{m_1^*}} {{H_1}({x_{{j_1}}},\lambda )} }},{{{\hat{\rho }} }_2}(\lambda ) = \frac{{ - m_2^*}}{{\sum \nolimits _{{j_2} = 1}^{m_2^*} {{H_2}({w_{{j_2}}},\lambda )} }}, {{{\hat{\rho }} }_3}(\lambda ) = \frac{{ - m_3^*}}{{\sum \nolimits _{{j_3} = 1}^{{m_3^*}} {{H_3}({z_{{j_3}}},\lambda )} }}. \end{aligned}$$
(9)

Inserting (9) in (8) provides us with

$$\begin{aligned} \begin{aligned} \zeta (\lambda )&= \left\{ {\frac{{A({x_{{j_1}}},{w_{{j_2}}},{z_{{j_3}}})}}{{({m_1^*} + {m_2^*}+ {m_3^*})}}} \right. - \sum \limits _{{j_1} = 1}^{m_1^*} {\frac{{({{{\hat{\rho }} }_1}(\lambda ) - 1)\left( {{{H'}_1}({x_{{j_1}}},\lambda )} \right) }}{{{H_1}({x_{{j_1}}},\lambda )({m_1^*} + {m_2^*} + {m_3^*})}}\,\,} \\&\quad - \sum \limits _{{j_2} = 1}^{{m_2^*}} {\frac{{({{{\hat{\rho }} }_2}(\lambda ) - 1)\left( {{{H'}_2}({w_{{j_2}}},\lambda )} \right) }}{{{H_2}({w_{{j_2}}},\lambda )({m_1^*}+ {m_2^*} + {m_3^*})}} - } {\left. { \sum \limits _{{j_3} = 1}^{m_3^*} {\frac{{({{{\hat{\rho }} }_3}(\lambda ) - 1)\left( {{{H'}_3}({z_{{j_3}}},\lambda )} \right) }}{{{H_3}({z_{{j_3}}},\lambda )({m_1^*} + {m_2^*} + {m_3^*})}}} } \right\} ^{ - 1}}, \\ \end{aligned} \end{aligned}$$
(10)

where, \({{\hat{\rho }} _i}(\lambda ),\,i = 1,2,3\) defined in (9). The MLE of \(\lambda\), say \({\hat{\lambda }}\), is determined from (10), by using a reasonable approximation approach. Consequently, \({{\hat{\rho }} _1},\,\,{{\hat{\rho }} _2}\) and \({{\hat{\rho }} _3}\) are produced by incorporating \({\hat{\lambda }}\) in Eq. (7). Therefore, \({{\hat{R}}_1},\) is supplied by including \({{\hat{\rho }} _1},\,\,{{\hat{\rho }} _2}\) and \({{\hat{\rho }} _3}\) in (5) as follows:

$$\begin{aligned} {{\hat{R}}_1} = \,\frac{{{{{\hat{\rho }} }_1}{{{\hat{\rho }} }_3}}}{{({{{\hat{\rho }} }_1} + {{{\hat{\rho }} }_2})({{{\hat{\rho }} }_1} + {{{\hat{\rho }} }_2} + {{{\hat{\rho }} }_3})}}. \end{aligned}$$

3.2 MPSE of \({R_1}\)

Reference [46] proposed the MPS technique, a potent alternative method for calculating the population parameters of continuous distributions. Consider the ordered items \({X_{(1)}},{X_{(2)}},\ldots ,{X_{(m_1^ * )}}\), \({W_{(1)}},{W_{(2)}},\ldots ,{W_{({m_2^*})}},\) and \({Z_{(1)}},{Z_{(2)}},\ldots ,{Z_{({m_3^*})}},\) constitute an SRS of sizes \(m_1^ *,{m_2}^ *,{m_3}^ *\), drawn from independent IKwD with parameters \((\lambda ,{\rho _1}),\) \((\lambda ,{\rho _2}),\) and \((\lambda ,{\rho _3}),\) respectively. Hence, the uniform spacings are defined by:

$$\begin{aligned} \begin{aligned} G(\Psi )&= {\left\{ {\prod \limits _{{i_1} = 1}^{m_1^ * + 1} {{D_{{i_1}}}(} \lambda ,{\rho _1})} \right\} ^{{1 / {(m_1^ * + 1)}}}}{\left\{ {\prod \limits _{{i_2} = 1}^{m_2^* + 1} {{D_{{i_2}}}(} \lambda ,{\rho _2})} \right\} ^{{1 / {(m_2^* + 1)}}}} \\&\quad \times {\left\{ {\prod \limits _{{i_3} = 1}^{{m_3}^ * + 1} {{D_{{i_3}}}(} \lambda ,{\rho _3})} \right\} ^{{1 / {(m_3^* + 1)}}}}, \\ \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} {D_{{i_j}}}(\lambda ,{\rho _j}) = \left\{ {\begin{array}{*{20}{c}} {F({\upsilon _{(0)}};\lambda ,{\rho _j}) = 0\,} \\ {F({\upsilon _{({i_j})}};\lambda ,{\rho _j}) - F({\upsilon _{({i_j} - 1)}};\lambda ,{\rho _j})} \\ {F({\upsilon _{(m_j^* + 1)}};\lambda ,{\rho _j})\,\, = 1} \end{array}}, \right. \end{aligned}$$
(11)

where \({i_j} = 1,2,...,m_j^* ,{\upsilon _{{i_j}}} \equiv \left( {{x_{{i_1}}},{w_{{i_2}}},{z_{{i_3}}}} \right) ,j = 1,2,3.\) The MPSEs of the unknown parameters \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) denoted by \({{\tilde{\rho }} _1},{{\tilde{\rho }} _2},{{\tilde{\rho }} _3},\) and \({\tilde{\lambda }}\) can be obtained by maximizing, with respect to \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) the following function:

$$\begin{aligned} \begin{aligned} \log G(\Psi )&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^ * + 1} {\log } \left[ {{{\left[ {{K_1}({x_{({i_1})}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {K_1^ * ({x_{({i_1} - 1)}},\lambda )} \right] }^{{\rho _1}}}} \right] \\&\quad + \frac{1}{{({m_2^*} + 1)}}\sum \limits _{{i_2} = 1}^{m_2^* + 1} {\log } \left[ {{{\left[ {{K_2}({w_{({i_2})}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {K_2^ * ({w_{({i_2} - 1)}},\lambda )} \right] }^{{\rho _2}}}} \right] \\&\quad + \frac{1}{{(m_3^* + 1)}}\sum \limits _{{i_3} = 1}^{{m_3^*} + 1} {\log } \left[ {{{\left[ {{K_3}({z_{({i_3})}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {\left[ {K_3^ * ({z_{({i_3} - 1)}},\lambda )} \right] } \right] }^{{\rho _3}}}} \right] , \\ \end{aligned} \end{aligned}$$
(12)

where, \({K_j}({\upsilon _{({i_j})}},\lambda ) = \left[ {1 - {{\left( {1 + {\upsilon _{({i_j})}}} \right) }^{ - \lambda }}} \right] ,\) \(K_{_j}^ * ({\upsilon _(}_{{i_j} - 1)},\lambda ) = \left[ {1 - {{\left( {1 + {\upsilon _{({i_j} - 1)}}} \right) }^{ - \lambda }}} \right] ,\) and \({\upsilon _{({i_j})}} = ({x_{{i_1}}},{w_{{i_2}}},{z_{{i_3}}}), j = 1,2,3.\) Equivalently these estimators can be obtained by differentiating (12) concerning \({\rho _j},j = 1,2,3,\) and \(\lambda\) as below:

$$\begin{aligned} \begin{aligned} \frac{{\partial \log G(\Psi )}}{{\partial {\rho _j}}} = \frac{1}{{({m_j^*} + 1)}}\sum \limits _{{i_j} = 1}^{({m_j^*} + 1)} {\left\{ {\frac{{{{\left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] }^{{\rho _j}}}\log \left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] }}{{{{\left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] }^{{\rho _j}}} - {{\left[ {K_{_j}^ * (\upsilon _{({{i_j} - 1)}},\lambda )} \right] }^{{\rho _j}}}}}} \right. } \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { - \frac{{{{\left[ {K_{_j}^ * (\upsilon _{({{i_j} - 1)}},\lambda )} \right] }^{{\rho _j}}}\log \left[ {K_{_j}^ * (\upsilon _{({{i_j} - 1)}},\lambda )} \right] }}{{{{\left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] }^{{\rho _j}}} - {{\left[ {K_{_j}^ * (\upsilon _{({{i_j} - 1)}},\lambda )} \right] }^{{\rho _j}}}}}} \right\} , \\ \end{aligned} \end{aligned}$$
(13)
$$\begin{aligned} \hspace{-0.5cm} \begin{aligned} \frac{{\partial \log G(\Psi )}}{{\partial \lambda }}&= \frac{1}{{(m_1^ * + 1)}}\sum _{{i_1} = 1}^{(m_1^ * + 1)} {\frac{{{{\ddddot{K}}_1}({x_{({i_1})}},\lambda ) - \ddddot{K}_1^ * ({x_{({i_1} - 1)}},\lambda )}}{{{{\left[ {{K_1}({x_{({i_1})}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {K_1^ * ({x_{({i_1} - 1)}},\lambda )} \right] }^{{\rho _1}}}}}} \\&\quad + \frac{1}{{({m_2^*} + 1)}}\sum \limits _{{i_2} = 1}^{({m_2^*} + 1)} {\frac{{{{\ddddot{K}}_2}({w_{({i_2})}},\lambda ) - \ddddot{K}_2^ * ({w_{({i_2} - 1)}},\lambda )}}{{{{\left[ {{K_2}({w_{({i_2})}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {K_2^ * ({w_{({i_2} - 1)}},\lambda )} \right] }^{{\rho _2}}}}}} \\&\quad + \frac{1}{{({m_3^*} + 1)}}\sum \limits _{{i_3} = 1}^{({m_3^*} + 1)} {\frac{{{{\ddddot{K}}_3}({z_{({i_3})}},\lambda ) - {{ {\ddddot{K}_3^ * ({z_{({i_3} - 1)}},\lambda )} }}}}{{{{\left[ {{K_3}({z_{({i_3})}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {K_3^ * ({z_{({i_3} - 1)}},\lambda )} \right] }^{{\rho _3}}}}}}, \\ \end{aligned} \end{aligned}$$
(14)

where, \({{\ddddot{K}}_j}({\upsilon _{({i_j})}},\lambda ) = \frac{\partial }{{\partial \lambda }}{\left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] ^{{\rho _j}}} = {\rho _j}{\left[ {{K_j}({\upsilon _{({i_j})}},\lambda )} \right] ^{{\rho _j} - 1}}{\left( {1 + {\upsilon _{({i_j})}}} \right) ^{ - \lambda }}\log \left( {1 + {\upsilon _{({i_j})}}} \right) ,\) and \(\ddddot K_j^*({\upsilon _{({i_j} - 1)}},\lambda ) = \frac{\partial }{{\partial \lambda }}{\left[ {K_j^ * ({\upsilon _{({i_j} - 1)}},\lambda )} \right] ^{{\rho _j}}} = {\rho _j}{\left[ {{K_j}({\upsilon _{({i_j} - 1)}},\lambda )} \right] ^{{\rho _j} - 1}}{\left( {1 + {\upsilon _{({i_j} - 1)}}} \right) ^{ - \lambda }}\log \left( {1 + {\upsilon _{({i_j} - 1)}}} \right) .\)

Equating the above derivatives with zero and solving them numerically, we obtain the MPSE of parameters. Inserting \({{\tilde{\rho }} _1},{{\tilde{\rho }} _2},{{\tilde{\rho }} _3},\) and \({\tilde{\lambda }}\) in (5), we can obtain the MPSE of \({R_1}\) as follows:

$$\begin{aligned} {{\tilde{R}}_1} = \,\frac{{{{{\tilde{\rho }} }_1}{{{\tilde{\rho }} }_3}}}{{({{{\tilde{\rho }} }_1} + {{{\tilde{\rho }} }_2})({{{\tilde{\rho }} }_1} + {{{\tilde{\rho }} }_2} + {{{\tilde{\rho }} }_3})}}. \end{aligned}$$

4 Estimation of \({R_2} = \,P[{W_{RSS}}< {X_{RSS}} < {Z_{RSS}}]\)

In this section, the MLE and MPSE of \({R_2},\) designed respectively by \({{\hat{R}}_2},\) and \({{\tilde{R}}_2},\) are established when the observed samples for both stresses and strength are collected from RSS.

4.1 MLE of \(R_2\)

Let \({X_t}_{\left( t \right) u}\), represents the \({t^{th}}\) order statistics (OS) of the \({t^{th}}\) sample, \(t = 1,2, \ldots ,{m_1}\), in the \({u^{th}}\) cycle, \(u = 1,2, \ldots , {s_x}\), \(m_1^ * = {m_1}{s_x}\) from IKwD \((\lambda ,{\rho _1}).\) Let \({W_k}_{\left( k \right) b}\), be the kth OS from IKwD \((\lambda ,{\rho _2})\) of \({k^{th}}\) sample, \(k = 1,2, \ldots ,{{m_2}}\), in the \({b^{th}}\) cycle, \(b = 1,2, \ldots , {s_w},\) \({m_2}^ * = {{m_2}}{s_w}\). Also, suppose that \({z_q}_{\left( q \right) b}\) \({Z_q}_{\left( q \right) d}\), be the \({q^{th}}\) OS from IKwD \((\lambda ,{\rho _3})\) of \({q^{th}}\) sample, \(q = 1,2, \ldots ,{{m_3}}\), in the \({d^{th}}\) cycle, \(d =1,2,\ldots , s_z\), \({m_3}^ * = {{m_3}}{s_z}\). Here, \({s_x},{s_w},\) and \({s_z}\) are the number of cycles, \(m_1\), \({m_2}\), and \({m_3}\) are the set sizes. For the sake of clarity, we refer to \({X_{tu}},{W_{kb}},\) and \({Z_{qd}}\) throughout the rest of the work rather than \({X_t}_{\left( t \right) u},{W_k}_{\left( k \right) b},\) and \({Z_q}_{\left( q \right) d}\). It’s important to note that the PDFs of the \({X_t}_{\left( t \right) u},{W_k}_{\left( k \right) b},\) and \({Z_q}_{\left( q \right) d}\) are, respectively, the PDFs of the \({t^{th}},{k^{th}}\) and \({q^{th}}\) OS, which were obtained as

$$\begin{aligned}{} & {} \begin{aligned} f({x_{tu}})&= \frac{{{m_1}!}}{{(t - 1)!({m_1} - t)!}}\lambda {\rho _1}{(1 + {x_{tu}})^{ - \lambda - 1}} \\&\quad \times {\left[ {{\Upsilon _{tu}}(\lambda )} \right] ^{{\rho _1}t - 1}}{\left[ {1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}} \right] ^{{m_1} - t}},0< {x_{tu}}< \infty , \\ \end{aligned}\\{} & {} \begin{aligned} f({w_{kb}})&= \frac{{{{m_2}}!\lambda {\rho _2}}}{{(k - 1)!({{m_2}} - k)!}}{(1 + {w_{kb}})^{ - \lambda - 1}}{\left[ {{\Xi _{kb}}(\lambda )} \right] ^{{\rho _2}k - 1}} \\&\quad \times {\left[ {1 - {{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2}}}} \right] ^{{{m_2}} - k}},0< {w_{kb}}< \infty , \end{aligned}\\{} & {} \begin{aligned} f({z_{qd}})&= \frac{{{{m_3}}!\lambda {\rho _3}}}{{(q - 1)!({{m_3}} - q)!}}{(1 + {z_{qd}})^{ - \lambda - 1}}{\left[ {{\textrm{B}_{qd}}\left( \lambda \right) } \right] ^{{\rho _3}q - 1}} \\&\quad \times {\left[ {1 - {{\left( {{\textrm{B}_{qd}}\left( \lambda \right) } \right) }^{{\rho _3}}}} \right] ^{{{m_3}} - q}},0< {z_{qd}} < \infty , \\ \end{aligned} \end{aligned}$$

where, \({\Upsilon _{tu}}(\lambda ) = \left[ {1 - {{\left( {1 + {x_{tu}}} \right) }^{ - \lambda }}} \right] ,\) \({\Xi _{kb}}(\lambda ) = \left[ {1 - {{\left( {1 + {w_{kb}}} \right) }^{ - \lambda }}} \right] ,\) and \({\textrm{B}_{qd}}\left( \lambda \right) = \left[ {1 - {{\left( {1 + {z_{qd}}} \right) }^{ - \lambda }}} \right] .\)

In this instance, the likelihood function \({L_2}(\Psi )\) is as follows:

$$\begin{aligned} {L_2}(\Psi ) \propto \prod \limits _{u = 1}^{{s_x}} {\prod \limits _{t = 1}^{{m_1}} {f({x_{tu}})} \prod \limits _{b = 1}^{{s_w}} {\prod \limits _{k = 1}^{{{m_2}}} {f({w_{kb}})} } } \prod \limits _{d = 1}^{{s_z}} {\prod \limits _{q = 1}^{{{m_3}}} {f({z_{qd}})} }. \end{aligned}$$

The log-likelihood function, say \({\ell _2}(\Psi ),\) based on RSS, is given by:

$$\begin{aligned} \begin{aligned}&{\ell _2}(\Psi ) \propto m_1^*\log ({\rho _1}) + (m_1^* + m_2^* + m_3^*)\log \lambda \\&\quad - \sum \limits _{u = 1}^{{s_x}} {\left[ {\sum \limits _{t = 1}^{{m_1}} {(\lambda + 1)\log (1 + {x_{tu}}) - ({\rho _1}t - 1)\log \left[ {{\Upsilon _{tu}}(\lambda )} \right] } } \right. } \\&\quad \left. { - ({m_1} - t)\log \left[ {1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}} \right] } \right] \, + m_2^*\log ({\rho _2}) \\&\quad - \sum \limits _{b = 1}^{{s_w}} {\left[ {\sum \limits _{k = 1}^{{{m_2}}} {(\lambda + 1)\log (1 + {w_{kb}}) - ({\rho _2}k - 1)\log \left[ {{\Xi _{kb}}(\lambda )} \right] } } \right. } \\&\quad \left. { - ({{m_2}} - k)\log \left[ {1 - {{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2}}}} \right] } \right] \, + m_3^*\log ({\rho _3}) \\&\quad - \sum \limits _{d = 1}^{{s_z}} {\left[ {\sum \limits _{q = 1}^{{{m_3}}} {(\lambda + 1)\log (1 + {z_{qd}}) - ({\rho _3}q - 1)\log \left[ {{\textrm{B}_{qd}}(\lambda )} \right] } } \right. } \\&\quad - ({{m_3}} - q)\log \left[ {1 - {{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{{\rho _3}}}} \right] . \\ \end{aligned} \end{aligned}$$

The MLEs of \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) are given by:

$$\begin{aligned}{} & {} \frac{{\partial {\ell _2}(\Psi )}}{{\partial {\rho _1}}} = \frac{{m_1^*}}{{{\rho _1}}} + \sum \limits _{u = 1}^{{s_x}} {\left[ {\sum \limits _{t = 1}^{{m_1}} {t\log \left[ {{\Upsilon _{tu}}(\lambda )} \right] - \frac{{({m_1} - t)\log \left( {{\Upsilon _{tu}}(\lambda )} \right) }}{{{{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{ - {\rho _1}}} - 1}}} } \right] }, \end{aligned}$$
(15)
$$\begin{aligned}{} & {} \frac{{\partial {\ell _2}(\Psi )}}{{\partial {\rho _2}}} = \frac{{{m_2^*}}}{{{\rho _2}}} + \sum \limits _{b = 1}^{{s_w}} {\left[ {\sum \limits _{k = 1}^{{{m_2}}} {k\log \left[ {{\Xi _{kb}}(\lambda )} \right] - \frac{{({{m_2}} - k)\log \left( {{\Xi _{kb}}(\lambda )} \right) }}{{{{\left( {{\Xi _{kb}}(\lambda )} \right) }^{ - {\rho _2}}} - 1}}} } \right] }, \end{aligned}$$
(16)
$$\begin{aligned}{} & {} \frac{{\partial {\ell _2}(\Psi )}}{{\partial {\rho _3}}} = \frac{{{m_3^*}}}{{{\rho _3}}} + \sum \limits _{d = 1}^{{s_z}} {\left[ {\sum \limits _{q = 1}^{{{m_3}}} {q\log \left[ {{\textrm{B}_{qd}}(\lambda )} \right] - \frac{{({{m_3}} - q)\log \left( {{\textrm{B}_{qd}}(\lambda )} \right) }}{{{{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{ - {\rho _3}}} - 1}}} } \right] }, \end{aligned}$$
(17)
$$\begin{aligned}{} & {} \frac{{\partial {\ell _2}(\Psi )}}{{\partial \lambda }} = \frac{{m_1^* + {m_2^*} + {m_3^*}}}{\lambda } \nonumber \\{} & {} \quad - \sum \limits _{u = 1}^{{s_x}} {\left[ {\sum \limits _{t = 1}^{{m_1}} {\left\{ {\log (1 + {x_{tu}})} \right\} } } \right. } \left[ 1+ {\frac{{({m_1} - t){\rho _1}{{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1} - 1}}{{\left( {1 + {x_{tu}}} \right) }^{ - \lambda }}}}{{1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}}}} \right. \nonumber \\{} & {} \quad \left. {\left. { - \frac{{({\rho _1}t - 1){{\left( {1 + {x_{tu}}} \right) }^{ - \lambda }}}}{{{\Upsilon _{tu}}(\lambda )}}} \right] } \right] \,\,\, - \sum \limits _{b = 1}^{{s_w}} {\left[ {\sum \limits _{k = 1}^{{{m_2}}} {\left\{ {\log (1 + {w_{kb}})} \right\} } } \right. } \nonumber \\{} & {} \quad \times \left. {\left[ 1+ {\frac{{({{m_2}} - k){\rho _2}{{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2} - 1}}{{(1 + {w_{kb}})}^{ - \lambda }}}}{{1 - {{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2}}}}} - \frac{{({\rho _2}k - 1){{(1 + {w_{kb}})}^{ - \lambda }}}}{{{\Xi _{kb}}(\lambda )}}} \right] } \right] \, \nonumber \\{} & {} \quad - \sum \limits _{d = 1}^{{s_z}} {\left[ {\sum \limits _{q = 1}^{{{m_3}}} {\left\{ {\log (1 + {z_{qd}})} \right\} \left[ {1+\frac{{({{m_3}} - q){\rho _3} {{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{{\rho _3} - 1}}{{(1 + {z_{qd}})}^{ - \lambda }}}}{{1 - {{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{{\rho _3}}}}}} \right. } } \right. } \nonumber \\{} & {} \quad \left. {\left. { - \frac{{({\rho _3}q - 1){{(1 + {z_{qd}})}^{ - \lambda }}}}{{{\textrm{B}_{qd}}(\lambda )}}} \right] } \right] . \end{aligned}$$
(18)

The MLEs of \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) could be obtained by setting (15)–(18) to zero and solving numerically, then obtaining \({{\hat{R}}_2}\) by plugging these MLEs into (5).

4.2 MPSE of \(R_2\)

Consider the ordered items \({X_{(1:m_{1}^*)}},{X_{(2:m_{1}^*)}},\ldots ,{X_{(m_{1}^*:m_{1}^*)}},\) \({W_{(1:m_2^*)}},{W_{(2:m_2^*)}},\ldots ,{W_{(m_2^*:m_2^*)}},\) and \({Z_{(1:m_3^*)}}\),

\({Z_{(2:m_3^*)}},\ldots ,{Z_{({m_3^*}:m_3^*)}},\) be RSS with sizes \(m_1^* = {m_1}{s_x}\), \(m_2^* = {{m_2}}{s_w}\) and \(m_3^* = {{m_3}}{s_z},\) respectively, where \({m_1},{{m_2}},{{m_3}}\) are set sizes while \({s_x},{s_w},{s_z}\) are cycles numbers drawn from independent IKwD with parameters \((\lambda ,{\rho _1}),\) \((\lambda ,{\rho _2}),\) and \((\lambda ,{\rho _3}).\) Hence, the uniform spacings

$$\begin{aligned} \begin{aligned} {G_1}(\Psi )&= {\left\{ {\prod \limits _{{i_1} = 1}^{m_1^ * + 1} {{\Delta _{{i_1}}}(} \lambda ,{\rho _1})} \right\} ^{{1 / {(m_1^ * + 1)}}}}{\left\{ {\prod \limits _{{i_2} = 1}^{{m_2^*} + 1} {{\Delta _{{i_2}}}(} \lambda ,{\rho _2})} \right\} ^{{1 / {({m_2^*}+ 1)}}}}\\&\quad \times {\left\{ {\prod \limits _{{i_3} = 1}^{{m_3^*} + 1} {{\Delta _{{i_3}}}(} \lambda ,{\rho _3})} \right\} ^{{1 / {({m_3^*} + 1)}}}}, \\ \end{aligned} \end{aligned}$$

where,

$$\begin{aligned} {\Delta _{{i_j}}}(\lambda ,{\rho _j}) = \left\{ {\begin{array}{*{20}{c}} {F({\omega _{(0:m_j^* )}};\lambda ,{\rho _j}) = 0\,} \\ {F({\omega _{({i_j}:m_j^* )}};\lambda ,{\rho _j}) - F({\omega _{({i_j} - 1:m_j^* - 1)}};\lambda ,{\rho _j})} \\ {F({\omega _{(m_j^* + 1)}};\lambda ,{\rho _j})\,\, = 1} \end{array}} \right. , \end{aligned}$$
(19)

and \({i_j} = 1,2,\ldots ,m_j^* ,{\omega _{({i_j}:m_j^*)}} \equiv \left( {{x_{({i_1}:m_1^ * )}},{w_{({i_2}:m_2^* )}},{z_{({i_3}:m_3^* )}}} \right) ;j = 1,2,3.\) The following function can be maximized with respect to \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) to yield the MPSEs of the unknown parameters \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\)

$$\begin{aligned} \begin{aligned} \log {G_1}(\Psi )&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^ * + 1} {\log } \left[ {{{\left[ {A{K_1}({x_{({i_1}:m_1^ * )}},\lambda )} \right] }^{{\rho _1}}}} \right. \\&\quad \left. { - {{\left[ {AK_1^ * ({x_{({i_1} - 1:m_1^ * )}},\lambda )} \right] }^{{\rho _1}}}} \right] \\&\quad + \frac{1}{{(m_2^* + 1)}}\sum \limits _{{i_2} = 1}^{{m_2^*} + 1} {\log } \left[ {{{\left[ {A{K_2}({w_{({i_2}:{m_2^*} )}},\lambda )} \right] }^{{\rho _2}}}} \right. \\&\quad \left. { - {{\left[ {{AK_2}^ * ({w_{({i_2} - 1:m_2^* )}},\lambda )} \right] }^{{\rho _2}}}} \right] \\&\quad + \frac{1}{{(m_3^* + 1)}}\sum \limits _{{i_3} = 1}^{{m_3^*} + 1} {\log } \left[ {{{\left[ {A{K_3}({z_{({i_3}:m_3^* )}},\lambda )} \right] }^{{\rho _3}}}} \right. \\&\quad \left. { - {{\left[ {\left[ {{AK_3}^ * ({z_{({i_3} - 1:m_3^* )}},\lambda )} \right] } \right] }^{{\rho _3}}}} \right] , \\ \end{aligned} \end{aligned}$$
(20)

where \(A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda ) = \left[ {1 - {{\left( {1 + {\omega _{({i_j}:m_j^*)}}} \right) }^{ - \lambda }}} \right] ,\) \(AK_{j}^ * ({\omega _(}_{{i_j} - 1:m_j^*)},\lambda ) = \left[ {1 - {{\left( {1 + {\omega _{({i_j} - 1:m_j^*)}}} \right) }^{ - \lambda }}} \right] .\)

Equivalently these estimators can be obtained by differentiating (20) concerning \({\rho _j},j = 1,2,3,\) and \(\lambda\) as below:

$$\begin{aligned}{} & {} \frac{{\partial \log {G_1}(\Psi )}}{{\partial {\rho _j}}} = \frac{1}{{m_j^* + 1}}\sum \limits _{{i_j} = 1}^{m_j^* + 1} {\frac{{{{\left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right] }^{{\rho _j}}}\log \left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right] }}{{{{\left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right] }^{{\rho _j}}} - {{\left[ {AK_{j}^ * ({\omega _(}_{{i_j} - 1:m_j^*)},\lambda )} \right] }^{{\rho _j}}}}}} \nonumber \\{} & {} \quad - \frac{1}{{m_j^* + 1}}\sum \limits _{{i_j} = 1}^{m_j^* + 1} {\frac{{{{\left[ {AK_{j}^ * ({\omega _(}_{{i_j} - 1:m_j^*)},\lambda )} \right] }^{{\rho _j}}}\log \left[ {AK_{j}^ * ({\omega _(}_{{i_j} - 1:m_j^*)},\lambda )} \right] }}{{{{\left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right] }^{{\rho _j}}} - {{\left[ {AK_{j}^ * ({\omega _(}_{{i_j} - 1:m_j^*)},\lambda )} \right] }^{{\rho _j}}}}}}, \end{aligned}$$
(21)
$$\begin{aligned}{} & {} \frac{{\partial \log {G_1}(\Psi )}}{{\partial \lambda }} = \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{(m_1^ * + 1)} {\frac{{A{{\ddddot{K}}_1}({x_{({i_1}:m_1^*)}},\lambda ) - A\ddddot{K}_1^ * ({x_{({i_1} - 1:m_1^*)}},\lambda )}}{{{{\left[ {{K_1}({x_{({i_1}:m_1^*)}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {K_1^ * ({x_{({i_1} - 1:m_1^*)}},\lambda )} \right] }^{{\rho _1}}}}}} \nonumber \\{} & {} \quad + \frac{1}{{({m_2}^ * + 1)}}\sum \limits _{{i_2} = 1}^{({m_2^*} + 1)} {\frac{{A{{\ddddot{K}}_2}({w_{({i_2}:{m_2^*})}},\lambda ) - A\ddddot{K}_2^ * ({w_{({i_2} - 1:{m_2^*})}},\lambda )}}{{{{\left[ {A{K_2}({w_{({i_2}:{m_2^*})}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {{AK_2}^ * ({w_{({i_2} - 1:{m_2^*})}},\lambda )} \right] }^{{\rho _2}}}}}} \nonumber \\{} & {} \quad + \frac{1}{{({m_3^*} + 1)}}\sum \limits _{{i_3} = 1}^{({m_3^*} + 1)} {\frac{{A{{\ddddot{K}}_3}({z_{({i_3}:{m_3^*})}},\lambda ) - A\ddddot{K}_3^ * ({z_{({i_3} - 1:{m_3^*})}},\lambda )}}{{{{\left[ {A{K_3}({z_{({i_3}:{m_3^*})}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {{AK_3}^ * ({z_{({i_3} - 1:{m_3^*})}},\lambda )} \right] }^{{\rho _3}}}}}}, \end{aligned}$$
(22)

where

$$\begin{aligned} \begin{gathered} A{\ddddot K_j}({\omega _{({i_j}:m_j^*)}},\lambda ) = \frac{\partial }{{\partial \lambda }}{\left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right]^{{\rho _j}}} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = {\rho _j}{\left[ {A{K_j}({\omega _{({i_j}:m_j^*)}},\lambda )} \right]^{{\rho _j} - 1}}{\left( {1 + {\omega _{({i_j}:m_j^*)}}} \right)^{ - \lambda }}\log \left( {1 + {\omega _{({i_j}:m_j^*)}}} \right), \hfill \\ \end{gathered} \end{aligned}$$

and

$$\begin{aligned} A\ddddot K_j^*({\upsilon _{({i_j} - 1:m_j^*)}},\lambda )= & {} \frac{\partial }{{\partial \lambda }}{\left[ {AK_j^ * ({\omega _{({i_j} - 1:m_j^*)}},\lambda )} \right] ^{{\rho _j}}} \\= & {} {\rho _j}{\left[ {A{K_j}({\omega _{({i_j} - 1:m_j^*)}},\lambda )} \right] ^{{\rho _j} - 1}} {\left( {1 + {\omega _{({i_j} - 1:m_j^*)}}} \right) ^{ - \lambda }}\log \left( {1 + {\omega _{({i_j} - 1:m_j^*)}}} \right) . \end{aligned}$$

Equating the above derivatives with zero and solving them numerically, we obtain the MPSE of parameters, and then by inserting these estimators in (5), we can obtain the MPSE of \({R_2}.\)

5 Estimation of \({R_3} = \,P[{W_{RSS}}< {X_{SRS}} < {Z_{RSS}}]\)

The MLE and MPSE for the situation where the strength data for X is obtained from SRS and the stress data for W and Z are obtained from RSS design are given in this section. Assuming that X, W,  and Z are all independent IKwD with parameters \((\lambda ,{\rho _1}),\) \((\lambda ,{\rho _2}),\) and \((\lambda ,{\rho _3}),\) respectively.

5.1 MLE of \(R_3\)

Let \({X_1},{X_2},\ldots ,{X_{m_1^*}},\) be a SRS observed from IKwD \((\lambda ,{\rho _1}).\) Let \({W_{kb}},\,\,k = 1,2, \ldots ,{{m_2}}\), \(b = 1,2, \ldots {s_w},\) and \(m_2^* = {{m_2}}{s_w}\) be the selected RSS from IKwD \((\lambda ,{\rho _2})\). Also, suppose that \({Z_{qd}},\,\,q = 1,2, \ldots ,{{m_3}}\), \(d = 1,2, \ldots {s_z},\) and \(m_3^* = {{m_3}}{s_z}\) from IKwD \((\lambda ,{\rho _3}).\) The likelihood function \({L_3}(\Psi )\) in this case is as follows:

$$\begin{aligned} \begin{aligned}&{L_3}(\Psi ) \propto \prod \limits _{{j_1} = 1}^{m_1^ * } {\lambda {\rho _1}{{(1 + {x_{{j_1}}})}^{ - \lambda - 1}}{{\left[ {{H_1}({x_{{j_1}}},\lambda )} \right] }^{{\rho _1} - 1}}} \\&\quad \times \prod \limits _{b = 1}^{{s_w}} {\prod \limits _{k = 1}^{{{m_2}}} {\lambda {\rho _2}} {{(1 + {w_{kb}})}^{ - \lambda - 1}}{{\left[ {{\Xi _{kb}}(\lambda )} \right] }^{{\rho _2}k - 1}}{{\left[ {1 - {{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2}}}} \right] }^{{{m_2}} - k}}} \\&\quad \times \prod \limits _{d = 1}^{{s_z}} {\prod \limits _{q = 1}^{{m_3} } {\lambda {\rho _3}{{(1 + {z_{qd}})}^{ - \lambda - 1}}{{\left[ {{\textrm{B}_{qd}}\left( \lambda \right) } \right] }^{{\rho _3}q - 1}}{{\left[ {1 - {{\left( {{\textrm{B}_{qd}}\left( \lambda \right) } \right) }^{{\rho _3}}}} \right] }^{{{m_3}} - q}}} }. \\ \end{aligned} \end{aligned}$$

The log-likelihood function, symbolized by \({\ell _3}(\Psi ),\) is presented as follows:

$$\begin{gathered} {\ell _3}(\Psi ) \propto m_1^*\ln ({\rho _1}) + (m_1^* + m_2^* + m_3^*)\log \lambda - (\lambda + 1)\sum\limits_{{j_1} = 1}^{m_1^*} {\log (1 + {x_{{j_1}}})} \hfill \\ \,\,+ ({\rho _1} - 1)\sum\limits_{{j_1} = 1}^{m_1^*} {\log {H_1}({x_{{j_1}}},\lambda )} + m_2^*\ln ({\rho _2})+ m_3^*\log ({\rho _3}) \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\, - \sum\limits_{b = 1}^{{s_w}} {\left[ {\sum\limits_{k = 1}^{{m_2}} {(\lambda + 1)\log (1 + {w_{kb}}) - ({\rho _2}k - 1)\log \left[ {{\Xi _{kb}}(\lambda )} \right] - ({m_2} - k)\log \left[ {1 - {{\left( {{\Xi _{kb}}(\lambda )} \right)}^{{\rho _2}}}} \right]} } \right]} \, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\, - \sum\limits_{d = 1}^{{s_z}} {\left[ {\sum\limits_{q = 1}^{{m_3}} {(\lambda + 1)\log (1 + {z_{qd}}) - ({\rho _3}q - 1)\log \left[ {{{\rm B}_{qd}}(\lambda )} \right] - ({m_3} - q)\log \left[ {1 - {{\left( {{{\rm B}_{qd}}(\lambda )} \right)}^{{\rho _3}}}} \right]} } \right]} . \hfill \\ \end{gathered}$$

By maximizing \({\ell _3}(\Psi )\) with respect to \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\), the MLEs of them are obtained. The first partial derivatives of \({\rho _1},{\rho _2},{\rho _3}\) are derived in (7), (16) and (17). The first partial derivative of \(\lambda\) is:

$$\begin{aligned} \begin{aligned} \frac{{\partial {\ell _3}(\Psi )}}{{\partial \lambda }}&= \frac{{{m_1^*} + {m_2^*} + {m_3^*}}}{\lambda } - \sum \limits _{{j_1} = 1}^{m_1^*} {{\text {log}}(1 + {x_{{j_1}}})} + \sum \limits _{{j_1} = 1}^{{m_1^*}} {\frac{{({\rho _1} - 1)\left( {{{H'}_1}({x_{{j_1}}},\lambda )} \right) }}{{{H_1}({x_{{j_1}}},\lambda )}}} \, \\&\quad - \sum \limits _{b = 1}^{{s_w}} \left[ \sum \limits _{k = 1}^{{{m_2}}} \left\{ {\log (1 + {w_{kb}})} \right\} \left[ 1+ {\frac{{({{m_2}} - k){\rho _2}{{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2} - 1}}{{(1 + {w_{kb}})}^{ - \lambda }}}}{{1 - {{\left( {{\Xi _{kb}}(\lambda )} \right) }^{{\rho _2}}}}}} \right. \right. \\&\quad \left. \left. { - \frac{{({\rho _2}k - 1)\,{{(1 + {w_{kb}})}^{ - \lambda }}}}{{{\Xi _{kb}}(\lambda )}}} \right] \right] \\&\quad + \sum \limits _{d = 1}^{{s_z}} \left[ \sum \limits _{q = 1}^{{{m_3}}} \left\{ {\log (1 + {z_{qd}})} \right\} \left[ 1+{\frac{{({\rho _3}q - 1){{(1 + {z_{qd}})}^{ - \lambda }}}}{{{\textrm{B}_{qd}}(\lambda )}}} \right. \right. \\&\quad \left. \left. { - \frac{{({{m_3}} - q){\rho _3} {{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{{\rho _3} - 1}}{{(1 + {z_{qd}})}^{ - \lambda }}}}{{1 - {{\left( {{\textrm{B}_{qd}}(\lambda )} \right) }^{{\rho _3}}}}}} \right] \right] . \\ \end{aligned} \end{aligned}$$
(23)

The MLEs of \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) are created by equating (7), (16), (17) and (23) to zero and numerically solving these equations. These MLEs are then inserted into (5) to produce \({{\hat{R}}_3}\).

5.2 MPSE of \(R_3\)

Consider \({X_{(1)}},{X_{(2)}},\ldots ,{X_{(m_{1}^*)}}\) be the ordered SRS of strength X of size \(m_{1}^*\) from IKwD \(\sim (\lambda ,{\rho _1}).\) Let \({W_{(1:m_2^*)}},{W_{(2:m_2^*)}},\ldots ,{W_{(m_2^*:m_2^*)}},\) and \({Z_{(1:m_3^*)}},{Z_{(2:m_3^*)}},\ldots ,{Z_{(m_3^*:m_3^*)}},\) be RSS of sizes \(m_2^* = {{m_2}}{s_w}\) and \(m_3^* = {{m_3}}{s_z},\) respectively, where \({m_2}, {m_3}\) are set sizes while \(s_w\), \(s_z\) are cycles numbers drawn from IKwD\(\sim (\lambda ,{\rho _2})\) and IKwD \(\sim (\lambda ,{\rho _3})\) where X, W,  and Z all operate independently. Hence, the uniform spacing in this case is as below:

$$\begin{aligned} \begin{aligned} {G_2}(\Psi )&= {\left\{ {\prod \limits _{{i_1} = 1}^{m_1^ * + 1} {{D_{{i_1}}}(} \lambda ,{\rho _1})} \right\} ^{{1 / {(m_1^ * + 1)}}}}{\left\{ {\prod \limits _{{i_2} = 1}^{m_2^* + 1} {{\Delta _{{i_2}}}(} \lambda ,{\rho _2})} \right\} ^{{1 / {(m_2^* + 1)}}}} \\&\quad \times {\left\{ {\prod \limits _{{i_3} = 1}^{m_3^* + 1} {{\Delta _{{i_3}}}(} \lambda ,{\rho _3})} \right\} ^{{1 / {(m_3^* + 1)}}}}, \end{aligned} \end{aligned}$$
(24)

where, \({D_{{i_1}}}(\lambda ,{\rho _1}),\) is defined in (11) for \(j=1\), \({\Delta _{{i_2}}}(\lambda ,{\rho _2})\) and \({\Delta _{{i_3}}}(\lambda ,{\rho _3})\) are defined in (19). The MPSEs of the unknown parameters \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) can be obtained by maximizing, with respect to \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) the following function:

$$\begin{aligned} \begin{aligned} \log {G_2}(\Psi )&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^ * + 1} {\log } \left[ {{{\left[ {{K_1}({x_{({i_1})}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {K_1^ * ({x_{({i_1} - 1)}},\lambda )} \right] }^{{\rho _1}}}} \right] \\&\quad + \frac{1}{{(m_2^* + 1)}}\sum \limits _{{i_2} = 1}^{m_2^* + 1} {\log } \left[ {{{\left[ {A{K_2}({w_{({i_2}:m_2^* )}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {{AK_2}^ * ({w_{({i_2} - 1:m_2^* )}},\lambda )} \right] }^{{\rho _2}}}} \right] \\&\quad + \frac{1}{{(m_3^*+ 1)}}\sum \limits _{{i_3} = 1}^{m_3^* + 1} {\log } \left[ {{{\left[ {A{K_3}({z_{({i_3}:m_3^* )}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {\left[ {{AK_3}^ * ({z_{({i_3} - 1:m_3^* )}},\lambda )} \right] } \right] }^{{\rho _3}}}} \right] . \\ \end{aligned} \end{aligned}$$
(25)

Equivalently these estimators can be obtained by differentiating (25) with respect to \({\rho _j},j = 1,2,3,\) and \(\lambda\). Note that MPSE of \({\rho _j},\) is obtained in (13) for \(j =1\), and (21) for \(j=\)2 and 3. The MPSE of \(\lambda\) is given by

$$\begin{aligned} \begin{aligned} \frac{{\partial \log {G_2}(\Psi )}}{{\partial \lambda }}&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^ * + 1} {\frac{{{{\ddddot{K}}_1}({x_{({i_1})}},\lambda ) - \ddddot{K}_1^ * ({x_{({i_1} - 1)}},\lambda )}}{{{{\left[ {{K_1}({x_{({i_1})}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {K_1^ * ({x_{({i_1} - 1)}},\lambda )} \right] }^{{\rho _1}}}}}} \\&\quad + \frac{1}{{m_2^* + 1}}\sum \limits _{{i_2} = 1}^{m_2^* + 1} {\frac{{A{{\ddddot{K}}_2}({w_{({i_2}:m_2^*)}},\lambda ) - A\ddddot{K}_2^ * ({w_{({i_2} - 1:m_2^*)}},\lambda )}}{{{{\left[ {A{K_2}({w_{({i_2}:m_2^*)}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {{AK_2}^ * ({w_{({i_2} - 1:m_2^*)}},\lambda )} \right] }^{{\rho _2}}}}}} \\&\quad + \frac{1}{{m_3^*+ 1}}\sum \limits _{{i_3} = 1}^{m_3^* + 1} {\frac{{A{{\ddddot{K}}_3}({z_{({i_3}:m_3^*)}},\lambda ) - {{ {A\ddddot{K}_3^ * ({z_{({i_3} - 1:m_3^*)}},\lambda )} }}}}{{{{\left[ {A{K_3}({z_{({i_3}:m_3^*)}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {{AK_3}^ * ({z_{({i_3} - 1:m_3^*)}},\lambda )} \right] }^{{\rho _3}}}}}.} \\ \end{aligned} \end{aligned}$$
(26)

Equating the derivatives in (13),(21) and(26) with zero and solving them numerically, we obtain the MPSE of parameters, then by inserting these estimators in (5), we can obtain the MPSE of \(R_3\).

6 Estimation of \({R_4} = \,P[{W_{SRS}}< {X_{RSS}} < {Z_{SRS}}]\)

In this section, the MLE and MPSE estimator of \(R_4\) are produced using data from the RRS design for X and the SRS design for W and Z. Assuming that X, W,  and Z are independent, where \(X\sim\)IKwD\((\lambda ,{\rho _1}),\) \(W \sim\)IKwD\((\lambda ,{\rho _2}),\) and \(Z\sim\)IKwD\((\lambda ,{\rho _3}).\)

6.1 MLE of \(R_4\)

Let \({X_{tu}},t = 1,2, \ldots ,{m_1},u = 1,2, \ldots {s_x},\) be RSS from IKwD \((\lambda ,{\rho _1})\). Also, suppose that \({w_1},{w_2},\ldots ,{w_{m_2^*}},\) and \({z_1},{z_2},\ldots ,{z_{m_3^*}},\) are SRS from the IKwD with parameters \((\lambda ,{\rho _2})\), and \((\lambda ,{\rho _3})\) respectively. The likelihood function in this case is given by:

$$\begin{aligned} \begin{aligned} {L_4}(\Psi )&\propto \prod \limits _{u = 1}^{{s_x}} {\prod \limits _{t = 1}^{{m_1}} {\lambda {\rho _1}} {{(1 + {x_{tu}})}^{ - \lambda - 1}}{{\left[ {{\Upsilon _{tu}}(\lambda )} \right] }^{{\rho _1}t - 1}}{{\left[ {1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}} \right] }^{{m_1} - t}}} \\&\quad \times \prod \limits _{{j_2} = 1}^{m_2^* } {\lambda {\rho _2}{{(1 + {w_{{j_2}}})}^{ - \lambda - 1}}{{\left[ {{H_2}({w_{{j_2}}},\lambda )} \right] }^{{\rho _2} - 1}}} \\&\quad \times \prod \limits _{{j_3} = 1}^{m_3^*} {\lambda {\rho _3}{{(1 + {z_{{j_2}}})}^{ - \lambda - 1}}{{\left[ {{H_3}({z_{{j_3}}},\lambda )} \right] }^{{\rho _3} - 1}}}. \\ \end{aligned} \end{aligned}$$

The log-likelihood function, say \({\ell _4}(\Psi ),\) is given by:

$$\begin{aligned} \begin{aligned} {\ell _4}(\Psi )&\propto \,m_1^*\log ({\rho _1}) + (m_1^* + m_2^* + m_3^*)\log \lambda \\&\quad - \sum \limits _{u = 1}^{{s_x}} {\left[ {\sum \limits _{t = 1}^{{m_1}} {(\lambda + 1)\log (1 + {x_{tu}}) - ({\rho _1}t - 1)\log \left[ {{\Upsilon _{tu}}(\lambda )} \right] } } \right. } \\&\quad \left. { - ({m_1} - t)\log \left[ {1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}} \right] } \right] \, + m_2^*\log ({\rho _2}) + m_3^*\log ({\rho _3}) - (\lambda + 1) \\&\quad \left[ {\sum \limits _{{j_2} = 1}^{m_2^*} {\log } \,(1 + {w_{{j_2}}}) + \sum \limits _{{j_3} = 1}^{m_3^*} {\log } \,(1 + {z_{{j_3}}})} \right] \\&\quad + ({\rho _2} - 1)\sum \limits _{{j_2} = 1}^{m_2^*} {\log {H_2}({w_{{j_2}}},\lambda ) + } ({\rho _3} - 1)\sum \limits _{{j_3} = 1}^{m_3^*} {\log {H_3}({z_{{j_3}}},\lambda )} . \\ \end{aligned} \end{aligned}$$

The first partial derivatives of \({\rho _1},\) is provided in (15) and \({\rho _2},{\rho _3}\) are supplied in (7). The partial derivative of \(\lambda\) results in the following

$$\begin{aligned} \begin{aligned} \frac{{\partial {\ell _4}(\Psi )}}{{\partial \lambda }}&= \frac{{m_1^* + m_2^* + m_3^*}}{\lambda } \\&\quad + \sum \limits _{u = 1}^{{s_x}} {\left[ {\sum \limits _{t = 1}^{{m_1}} {\left\{ {\log (1 + {x_{tu}})} \right\} \left[ 1+ {\frac{{({\rho _1}t - 1){{\left( {1 + {x_{tu}}} \right) }^{ - \lambda }}}}{{{\Upsilon _{tu}}(\lambda )}}} \right. } } \right. } \\&\quad \left. {\left. { - \frac{{({m_1} - t){\rho _1}{{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1} - 1}}{{\left( {1 + {x_{tu}}} \right) }^{ - \lambda }}}}{{1 - {{\left( {{\Upsilon _{tu}}(\lambda )} \right) }^{{\rho _1}}}}}} \right] } \right] \\&\quad - \left[ {\sum \limits _{{j_2} = 1}^{m_2^*} {\log } \,(1 + {w_{{j_2}}}) + \sum \limits _{{j_3} = 1}^{m_3^*} {\log } \,(1 + {z_{{j_3}}})} \right] \, \\&\quad + \sum \limits _{{j_2} = 1}^{m_2^*} {\frac{{({\rho _2} - 1)\left( {{{H'}_2}({w_{{j_2}}},\lambda )} \right) }}{{{H_2}({w_{{j_2}}},\lambda )}}} + \sum \limits _{{j_3} = 1}^{m_3^*} {\frac{{({\rho _3} - 1)\left( {{{H'}_3}({z_{{j_3}}},\lambda )} \right) }}{{{H_3}({z_{{j_3}}},\lambda )}}}. \\ \end{aligned} \end{aligned}$$
(27)

Setting (7), (15) and (27) to zero and solving numerically yields the MLEs of \({\rho _1},{\rho _2},{\rho _3}\) and \(\lambda\), as a result, \({{\hat{R}}_4}\) is determined after putting the resulted MLEs in (5).

6.2 MPSE of \(R_4\)

Let \({x_{(1:m_{1}^*)}},{x_{(2:m_{1}^*)}},\ldots ,{x_{(m_{1}^*:m_{1}^*)}}\), be RSS of size drawn from IKwD\(\sim (\lambda ,{\rho _1})\). Consider the ordered SRS items \({w_{(1)}},{w_{(2)}},\ldots ,{w_{m_2^*}}\) and \({z_{(1)}},{z_{(2)}},\ldots ,{z_{m_3^*}}\) of size \(m_2^*\) and \(m_3^*\) drawn from IKwD\(\sim (\lambda ,{\rho _2})\) and IKwD\(\sim (\lambda ,{\rho _3})\) where X, W,  and Z operate independently. Hence, the uniform spacing

$$\begin{aligned} {G_3}(\Psi )= & {} {\left\{ {\prod \limits _{{i_1} = 1}^{m_1^ * + 1} {{\Delta _{{i_1}}}(} \lambda ,{\rho _1})} \right\} ^{{1 / {(m_1^ * + 1)}}}}{\left\{ {\prod \limits _{{i_2} = 1}^{m_2^* + 1} {{D_{{i_2}}}(} \lambda ,{\rho _2})} \right\} ^{{1 / {(m_2^* + 1)}}}} \nonumber \\{} & {} \times {\left\{ {\prod \limits _{{i_3} = 1}^{m_3^* + 1} {{D_{{i_3}}}(} \lambda ,{\rho _3})} \right\} ^{{1 / {(m_3^* + 1)}}}}, \end{aligned}$$
(28)

where, \({\Delta _{{i_1}}}(\lambda ,{\rho _j})\) for \(j=1\) is in defined (19), \({D_{{i_2}}}(\lambda ,{\rho _2}),\) and \({D_{{i_3}}}(\lambda ,{\rho _3})\) given in (11). The MPSEs of the unknown parameters \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) can be obtained by maximizing, with respect to \({\rho _1},{\rho _2},{\rho _3},\) and \(\lambda\) the following function:

$$\begin{aligned} \begin{aligned} \log {G_3}(\Psi )&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^ * + 1} {\log } \left[ {{{\left[ {A{K_1}({x_{({i_1}:m_1^ * )}},\lambda )} \right] }^{{\rho _1}}} - {{\left[ {AK_1^ * ({x_{({i_1} - 1:m_1^ * )}},\lambda )} \right] }^{{\rho _1}}}} \right] \\&\quad + \frac{1}{{(m_2^ *+ 1)}}\sum \limits _{{i_2} = 1}^{m_2^ * + 1} {\log } \left[ {{{\left[ {{K_2}({w_{({i_2})}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {K_2^ * ({w_{({i_2} - 1)}},\lambda )} \right] }^{{\rho _2}}}} \right] \\&\quad + \frac{1}{{(m_3^ *+ 1)}}\sum \limits _{{i_3} = 1}^{m_3^ * + 1} {\log } \left[ {{{\left[ {{K_3}({z_{({i_3})}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {\left[ {K_3^ * ({z_{({i_3} - 1)}},\lambda )} \right] } \right] }^{{\rho _3}}}} \right] . \\ \end{aligned} \end{aligned}$$
(29)

Equivalently these estimators can be obtained by differentiating (29) with respect to \({\rho _j},j = 1,2,3,\) and \(\lambda\). Note that MPSE of \({\rho _j}\) are obtained in (13) for \(j =2, 3,\) and (21) for \(j=1\). The MPSE of \(\lambda\) is given by:

$$\begin{aligned} \begin{aligned} \frac{{\partial \log {G_3}(\Psi )}}{{\partial \lambda }}&= \frac{1}{{(m_1^ * + 1)}}\sum \limits _{{i_1} = 1}^{m_1^* + 1} {\left[ {\frac{{{{\left[ {A{K_1}({x_{({i_1}:m_1^*)}}),\lambda )} \right] }^{{\rho _1}}}\log \left[ {A{K_1}({x_{({i_1}:m_1^*)}}),\lambda )} \right] }}{{{{\left[ {A{K_1}({x_{({i_1}:m_1^*)}}),\lambda )} \right] }^{{\rho _1}}} - {{\left[ {AK_{1}^ * ({x_(}_{{i_1} - 1:m_1^*)}),\lambda )} \right] }^{{\rho _1}}}}}} \right. } \\&\quad \left. { - \frac{{{{\left[ {A{K_1}({x_{({i_1-1}:m_1^*)}}),\lambda )} \right] }^{{\rho _1}}}\log \left[ {A{K_1}({x_{({i_1-1}:m_1^*)}}),\lambda )} \right] }}{{{{\left[ {A{K_1}({x_{({i_1}:m_1^*)}}),\lambda )} \right] }^{{\rho _1}}} - {{\left[ {AK_{1}^ * ({x _(}_{{i_1} - 1:m_1^*)}),\lambda )} \right] }^{{\rho _1}}}}}} \right] \\&\quad + \frac{1}{{(m_2^* + 1)}}\sum \limits _{{i_2} = 1}^{m_2^* + 1} {\frac{{{{\ddddot{K}}_2}({w_{({i_2})}},\lambda ) - \ddddot{K}_2^ * ({w_{({i_2} - 1)}},\lambda )}}{{{{\left[ {{K_2}({w_{({i_2})}},\lambda )} \right] }^{{\rho _2}}} - {{\left[ {K_2^ * ({w_{({i_2} - 1)}},\lambda )} \right] }^{{\rho _2}}}}}} \, \\&\quad + \frac{1}{{({m_3}^ * + 1)}}\sum \limits _{{i_3} = 1}^{m_3^* + 1} {\frac{{{{\ddddot{K}}_3}({z_{({i_3})}},\lambda ) - \ddddot{K}_3^ * ({z_{({i_3} - 1)}},\lambda )}}{{{{\left[ {{K_3}({z_{({i_3})}},\lambda )} \right] }^{{\rho _3}}} - {{\left[ {K_3^ * ({z_{({i_3} - 1)}},\lambda )} \right] }^{{\rho _3}}}}}}. \\ \end{aligned} \end{aligned}$$

Equating the above derivatives with zero and solving them numerically, we obtain the MPSE of parameters, then by inserting these estimators in (5), we can obtain the MPSE of \(R_4\).

7 Simulation Investigation

This section conducts a thorough simulation study to examine how different estimators behave when subjected to the specified sampling techniques. For the ML and MPS estimation methods, the mean squared error (MSE) and the absolute bias (AB) were used as precision measurements. The relative efficiency (RE) is also used to compare each example to Case 1 in each instance. The algorithm can be broken down into the following phases using the MathCAD program:

  1. 1.

    The true parameters values of \(({\rho _1},{\rho _2},{\rho _3},\lambda )\) are selected as (2.5, 0.8, 5, 0.5), (1.5, 0.5, 6, 0.5) and (2, 0.2, 12, 0.5). The corresponding values of R are 0.456, 0.563, and 0.768 respectively.

  2. 2.

    The SRS of X, W,  and Z,  represented by \({x_1},{x_2},\ldots ,{x_{m_1^*}},\) \({w_1},{w_2},\ldots ,{w_{m_2^*}},\) and \({z_1},{z_2},...,{z_{m_3^*}}\) where \((m_{^2}^ *,m_{^1}^ *,m_{^3}^ * ) =\) (10,10,10), (20,20,20), (30,30,30), (20,10,20), (30,10,30), (10,20,10), (10,30,10), (30,20,30), (20,30,20).

  3. 3.

    The corresponding RSSs of X, W,  and Z are represented, respectively by:

    1. (a)

      \({X_t}_{\left( t \right) u}\), where \(t = 1,2, \ldots ,{m_1}\), in the \({u^{th}}\) cycle, \(u = 1,2, \ldots {s_x}\), \(m_1^ * = {m_1}{s_x}\),

    2. (b)

      \({W_k}_{\left( k \right) b}\), where \(k = 1,2, \ldots ,{{m_2}}\), in the \({b^{th}}\) cycle, \(b = 1,2, \ldots {s_w}\), \(m_2^ * = {{m_2}}{s_w}\),

    3. (c)

      \({Z_q}_{\left( q \right) d}\), where \(q = 1,2, \ldots ,{{m_3}}\), in the \({d^{th}}\) cycle, \(d = 1,2, \ldots {s_z}\), \(m_3^ *= {{m_3}}{s_z}\),

    where set sizes; \(({{m_2}},{m_1},{{m_3}}) =\) (2,2,2), (4,4,4), (6,6,6), (4,2,4), (6,2,6), (2,4,2), (2,6,2), (6,4,6), and (4,6,4), number of cycles \({s_x} = {s_w} = {s_z} = 5\). Hence, the sample sizes are \((m_{^2}^ *,m_{^1}^ *,m_{^3}^ *) =\) (10,10,10), (20,20,20), (30,30,30), (20,10,20), (30,10,30), (10,20,10), (10,30,10), (30,20,30), (20,30,20).

  4. 4.

    Generate 1000 SRS and RSS of \(X\sim\)IKwD\(({\rho _1},\lambda )\), \(W\sim\)IKwD\(({\rho _2},\lambda )\) and \(Z\sim\)IKwD\(({\rho _3},\lambda )\) using inversion method.

  5. 5.

    Four sampling cases are studied such that:

    1. (a)

      Case 1: \(P({W_{SRS}}< {X_{SRS}} < {Z_{SRS}})\).

    2. (b)

      Case 2: \(P({W_{RSS}}< {X_{RSS}} < {Z_{RSS}})\).

    3. (c)

      Case 3: \(P({W_{RSS}}< {X_{SRS}} < {Z_{RSS}})\).

    4. (d)

      Case 4: \(P({W_{SRS}}< {X_{RSS}} < {Z_{SRS}})\).

  6. 6.

    The parameter estimates, together with their reliability estimates \({{\hat{R}}_1},{{\hat{R}}_2},{{\hat{R}}_3}\) and \({{\hat{R}}_4}\), are computed for ML method and \({{\tilde{R}}_1},{{\tilde{R}}_2},{{\tilde{R}}_3}\) and \({{\tilde{R}}_4}\) are calculated for MPS method.

  7. 7.

    The efficiencies of different estimates under selective schemes with respect to SRS are defined by,

    \(R{E_2}({\hat{R}}) = \frac{{ML\,MS{E_{{R_1}}}}}{{ML\,MS{E_{{R_2}}}}},\) \(R{E_3}({\hat{R}}) = \frac{{ML\,MS{E_{{R_1}}}}}{{ML\,MS{E_{{R_3}}}}},\) and \(R{E_4}({\hat{R}}) = \frac{{ML\,MS{E_{{R_1}}}}}{{ML\,MS{E_{{R_4}}}}}.\)

    Also,

    \(R{E^*}_2({\tilde{R}}) = \frac{{MPS\,MS{E_{{R_1}}}}}{{MPS\,MS{E_{{R_2}}}}},\) \(R{E^*}_3({\tilde{R}}) = \frac{{MPS\,MS{E_{{R_1}}}}}{{MPS\,MS{E_{{R_3}}}}},\) and \(R{E^*}_4({\tilde{R}}) = \frac{{MPS\,MS{E_{{R_1}}}}}{{MPS\,MS{E_{{R_4}}}}},\)

    Finally, relative efficiency of \({\hat{R}}\) with respect to \({\tilde{R}}\) are also calculated. Tables 1, 2, 3, 4, 5, and 6 provide a summary of the AB, MSE, and RE values.

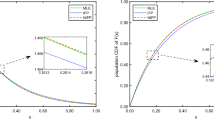
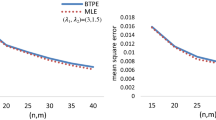
The numerical results shown in Tables 1, 2, 3, 4, 5, 6 and Figs. 3, 4, 5, 6, 7, 8, 9, 10 allow us to draw the following conclusions:

  1. 1.

    Tables 3 and 5 show that reliability estimates acquired using the RSS technique are often more effective than reliability estimates obtained using the SRS scheme, where \(R=\) 0.456, 0.563 and 0.768.

  2. 2.

    The MSEs of \({{\hat{R}}_3} = P\left( {{W_{RSS}}< {X_{SRS}} < {Z_{RSS}}} \right)\) are often more efficient than \({{\hat{R}}_4} = P\left( {{W_{SRS}}< {X_{RSS}} < {Z_{SRS}}} \right)\) at true value R = 0.563, (Table 4).

  3. 3.

    Figures 3 and 4 show that, in the majority of circumstances, the MSEs of \({{\tilde{R}}_1},{{\tilde{R}}_2},{{\tilde{R}}_3}\) and \({{\tilde{R}}_4}\) decrease as sample size increases. Additionally, we note that Case 1 has the highest MSE values compared to the others.

  4. 4.

    As seen in Fig. 4, Case 3 has the lowest MSE values at true value R = 0.768 when compared to the other cases.

  5. 5.

    The MSE of the system reliability \({{\tilde{R}}_3}\) has the least MSE at R =0.563 when \((m_2^*,m_1^ *,m_3^* ) =\) (20,20,20) and (30,30,30) as shown in Fig. 3.

  6. 6.

    The MSE of the system reliability \({{\tilde{R}}_3}\) has the least MSE at R = 0.768 at sample sizes (10,10,10), (20,20,20) and (30,30,30) as shown in Fig. 4.

  7. 7.

    The MSE of \({{\hat{R}}_1},{{\hat{R}}_2},{{\hat{R}}_3},{{\hat{R}}_4}\) decreases as the actual value of R increases as seen in Figs. 5 and 6.

  8. 8.

    As illustrated in Figs. 5 and 6, the MSE in Case 1 of \({{\hat{R}}_1}\) has the largest values when compared to the other cases.

  9. 9.

    Figure 5 shows that the system reliability \({{\hat{R}}_3}\) has the least MSE at R = 0.456 and 0.768 at sample sizes (10,10,10), while Fig. 6 shows that the MSE of the system reliability \({{\hat{R}}_3}\) has the least MSE at R = 0.456 and 0.563 at sample sizes (30,10,30).

  10. 10.

    For chosen sample size values (20, 20, 20) and different real values of R under the MPS method, we conclude that using RSS strengths and stress random variables (Case 2) is more efficient than the others, as illustrated in Fig. 7.

  11. 11.

    The RE for \({\hat{R}}\) increases as the sample size increases at R = 0.456 and R = 0.563 respectively (see for example Fig. 8).

  12. 12.

    Figure 8 indicates that Case 2 is the most efficient at sample sizes (10,10,10), (20,20,20) while Case 3 is the most efficient at sample sizes (30,30,30).

  13. 13.

    Figure 9 explains that case C2 is the most efficient at sample sizes (20,20,20) and (30,30,30) while Case 3 is the most efficient at sample size (10,10,10).

  14. 14.

    Figure 10 shows that MLE of R has a smaller MSE than the MPSE at R = 0.768 for sample size (30,30,30), also it indicates that case 2 has the least MSE compared to the other cases for both MLE and MPSE.

  15. 15.

    It is clear from Tables 7, 8 and 9 that the ML method is preferred than the MPS method in most of the situations except at true value \(R =0.456\) when the observed samples from stresses and strength data are all drawn from RSS (Case 2).

Table 1 Statistical measures of reliability estimators when strength and stresses are similar having SRS or RSS schemes at R = 0.456
Full size table
Table 2 Statistical measures of reliability estimators when strength and stresses are different having SRS and RSS schemes at R = 0.456
Full size table
Table 3 Statistical measures of reliability estimators when strength and stresses are similar having SRS or RSS schemes at R = 0.563
Full size table
Table 4 Statistical measures of reliability estimators when strength and stresses are different having SRS and RSS schemes at R = 0.563
Full size table
Table 5 Statistical measures of reliability estimators when strength and stresses are similar having SRS or RSS schemes R = 0.768
Full size table
Table 6 Statistical measures of reliability estimators when strength and stresses are different having SRS and RSS schemes at R = 0.768
Full size table
Table 7 Efficiency of reliability estimators at R = 0.456
Full size table
Table 8 Efficiency of reliability estimators at R = 0.563
Full size table
Table 9 Efficiency of reliability estimators at R = 0.768
Full size table
Table 10 Reliability estimates of the data sets based on various sampling techniques
Full size table
Fig. 3
figure 3

MSE of \({{\tilde{R}}_1},{{\tilde{R}}_2},{{\tilde{R}}_3},{{\tilde{R}}_4}\) at R = 0.563

Full size image
Fig. 4
figure 4

MSE of \({{\tilde{R}}_1},{{\tilde{R}}_2},{{\tilde{R}}_3},{{\tilde{R}}_4}\) at R = 0.768

Full size image
Fig. 5
figure 5

MSE of \({{\hat{R}}_1},{{\hat{R}}_2},{{\hat{R}}_3},{{\hat{R}}_4}\) for different values of R at (10, 10, 10)

Full size image
Fig. 6
figure 6

MSE of \({{\hat{R}}_1},{{\hat{R}}_2},{{\hat{R}}_3},{{\hat{R}}_4}\) for different values of R at (30, 10, 30)

Full size image
Fig. 7
figure 7

MSE of \({{\tilde{R}}_1},{{\tilde{R}}_2},{{\tilde{R}}_3},{{\tilde{R}}_4}\) for sample size (20, 20, 20) at different values of R

Full size image
Fig. 8
figure 8

\(RE({\hat{R}})\) comparison of different sample sizes at R = 0.456

Full size image
Fig. 9
figure 9

\(RE({\hat{R}})\) comparison of different sample sizes at R = 0.563

Full size image
Fig. 10
figure 10

MSE comparison of different cases at R = 0.768 and sample size (30,30,30)

Full size image

8 Application

This section considered and described in details three data sets to illustrate the usefulness of the proposed models. The first application is a real data set obtained from [47]. It consists of thirty successive values of March precipitation (in inches) in Minneapolis/St Paul. The second data application was given by [48]. The data set refers to the time between failures for repairable items. The third data application is the vinyl chloride data obtained from clean upgrading, and monitoring wells in mg/L; this data set was used by [49].

Data Set I: X \(m_1^*\; = \;30\)

0.77

1.74

0.81

1.2

1.95

1.2

0.47

1.43

3.37

2.2

3

3.09

1.51

2.1

0.52

1.62

1.31

0.32

0.59

0.81

2.81

1.87

1.18

1.35

4.75

2.48

0.96

1.89

0.9

2.05

Data Set II: W \(m_2^*\; = \;30\)

1.43

0.11

0.71

0.77

2.63

1.49

3.46

2.46

0.59

0.74

1.23

0.94

4.36

0.4

1.74

4.73

2.23

0.45

0.7

1.06

1.46

0.3

1.82

2.37

0.63

1.23

1.24

1.97

1.86

1.17

Data Set III: Z \(m_3^*\; = \;34\)

5.1

1.2

1.3

0.6

0.5

2.4

0.5

1.1

8

0.8

6.8

0.2

0.4

0.6

0.9

0.4

2

0.5

5.3

3.2

2.7

2.9

1.2

0.4

2.5

2.3

1

0.2

0.1

0.1

1.8

0.9

2

4

  

The three data sets were tested by Ref. [50] who showed that the IKwD fits this data well. Based on the foregoing theoretical conclusions, the analysed real data sets are sampled using both the RSS and SRS techniques. The reliability estimates from the IKwD are shown in Table 10 for various set size values based on five cycles and four various scenarios. The R-package RSS sampling is used to create the RSS and SRS using data sets I, II, and III. Based on these data sets I, II and III, the initial PDF shapes using the non-parametric kernel density estimation approach are shown in Figs. 11, 12 and 13. From these figures, it can be seen that the obtained PDF has an asymmetric shape. The quantile-quantile (QQ) plot is used to examine the normality condition (see Figs. 11, 12 and 13). The boxplot can also be used to identify outliers, as can be seen in Figs. 11, 12 and 13

Fig. 11
figure 11

Some non-parametric plots for the data set I

Full size image
Fig. 12
figure 12

Some non-parametric plots for the data set II

Full size image
Fig. 13
figure 13

Some non-parametric plots for the data set III

Full size image

9 Summary and Conclusion

Systems usually perform badly in several real-world scenarios because of the demanding operational circumstances. Researchers generally pay little attention to the fact that systems usually fail to carry out their intended functions when they are in their most extreme functioning states lower, higher, or both. This article’s goal is to construct an inference for the reliability function in situations where SS variables have inverted Kumaraswamy distributions based on RSS and SRS methodologies. As a result, the issue of ML and MPS procedures are used in estimating the SS function, R, if W, X, and Z are drawn from three separate independent inverted Kumaraswamy distributions under four cases; that is, case 1: \({R_1} = \,P[{W_{SRS}}< {X_{SRS}} < {Z_{SRS}}]\), Case 2: \({R_2} = \,P[{W_{RSS}}< {X_{RSS}} < {Z_{RSS}}]\), Case 3: \({R_3} = \,P[{W_{RSS}}< {X_{SRS}} < {Z_{RSS}}]\) and Case 4: \({R_4} = \,P[{W_{SRS}}< {X_{RSS}} < {Z_{SRS}}]\); for both methodologies is the subject of this article. To assess the effectiveness of the reliability estimators of the four models, a numerical study is conducted, and it is discovered that all reliability estimates perform better as the set sizes increase in the four cases. In general, we may deduce that models including the reliability estimators (Case 2, 3, and 4) via RSS are superior to the reliability estimator in Case 1 via SRS methodology for both methods, in the majority of situations. The efficiency of the SS reliability function improves as the set size increases. Application to real data has been analyzed for more information. Further research will consider the Bayesian estimation technique of \(R=P(W<X<Z\)) in case of imperfect ranking.