1 Introduction

The novel Coronavirus is a highly contagious viral strain found in late 2019, and the pneumonia caused by this virus was named novel Coronavirus disease 2019 (Covid-19) [1]. Typical symptoms of cases infected by Covid-19 include fever, fatigue, dry cough, etc. [2], and severe cases may result in respiratory distress syndrome or even death [3]. The main transmission routes of the Covid-19 are droplet transmission, contact transmission, and aerosol transmission [4]. The virus is characterized by rapid transmission, wide infection range, random mutation in its RNA, and other characteristics, and the prevention and control of its transmission is extremely difficult. The epidemic has been lingering around the world for more than three years, and fast-transmitting variants have been still affecting different regions. These showed that the Covid-19, no matter what kinds of new virus lines evolve or prevail, will continue to pose a critical threat to human life and health in near future.

Currently, conducting quantitative research and theoretical analysis on the spread of Covid-19 is essential for predicting its trends and implementing appropriate control measures. When it comes to epidemic forecasting, mathematical models play a crucial role in simulating the transmission dynamics of the outbreak. A well-designed mathematical model not only allows for the analysis of the transmission patterns of the epidemic and prediction of its trajectory but also offers valuable insights for epidemic prevention and control efforts. By leveraging mathematical models, informed recommendations can be made for future prevention and control strategies.

The traditional SEIR model considers the impact of factors such as contact rate, incidence rate, and latent cases on the epidemic. Hethcote discussed involving the basic reproduction number \(R_0\), the contact number \(\sigma \), and the replacement number \(R\) are reviewed for the classic SIR epidemic and endemic models [5]. Rock et al. focused on three critical aspects : heterogeneously structured populations, stochasticity, and spatial structure [6]. In the case of the Covid-19, different nations have implemented prevention and control measures, which to certain extent have contributed to hindering the Covid-19 transmission. However, these prevention and control measures have not been fully considered by traditional infectious disease models. It is not weird that using the traditional SEIR model could result in a large deviation between the prediction results and the number of infected cases.

Actually, many models were developed to describe the transmission of the Covid-19. Kuhl brought together modern concepts in mathematical epidemiology, computational modeling, physics-based simulation, data science, and machine learning to understand the outbreak dynamics and outbreak control of COVID-19 [7]. Frank [8] analyzed COVID-19 outbreaks in various countries around the globe, made use of mathematical models of epidemiology such as the SIR and SEIR models, and discussed the impacts of measures implemented to stop the spread of COVID-19 disease. Gatto [9] accounted for uncertainty in epidemiological reporting, and time dependence of human mobility matrices and awareness-dependent exposure probabilities and draw scenarios of different containment measures and their impact. Ngonghala et al. [10] developed a new mathematical model to assess the population-level impact of control and mitigation strategies, and emphasized the important role social-distancing plays in curtailing the burden of COVID-19. Yang Z et al. [11] proposed a M-SEIR model based on the improved SEIR model. Based on the M-SEIR model, Wang J et al. [12] proposed a CSPE model with the community as the basic forecasting unit. Martcheva [13] proposed quarantine and isolation were typically modeled by introducing separate classes into the model. Wei Y et al. [14] established a SEIR+CAQ transmission dynamics model, considering the transmission mechanism, infection spectrum, and isolation measures. According to the actual situation in China, Zhao X et al. [15] added the transmission process of latent tracking admission and morbidity tracking admission on the basis of the traditional SEIR model to depict the development trend of the epidemic and created a CSEIR model. By assuming that infected but undetected individuals are sent for quarantine during the incubation period, Pal. D [16] proposed a SEQIR model to assess and manage the outbreak of the infectious disease Covid-19. Daniele P et al. [17] developed a SPQEIR model to link intervention categories against epidemic spread to epidemiological model compartments. Giulia G et al. [18] developed SIDARTHE model discriminates between infected individuals depending on whether they have been diagnosed and on the severity of their symptoms, this delineation also helps to explain misperceptions of the case fatality rate and of the epidemic spread. Luca G et al. [19] introduced a framework to quantify how the uncertainty in the data affects the determination of the parameters and the evolution of the unmeasured variables of a given model. Francoise K et al. [20] extended the SEIR model, and considered how the interplay between vaccinations and social measures could shape infections and hospitalizations.

While mathematical models serve as valuable tools for understanding epidemics and guiding response strategies, they are not without their limitations. Firstly, the spread of Covid-19 is influenced by a multitude of factors such as policy adjustments, levels of isolation, quality of medical care, and adherence to personal protective measures. These factors can introduce significant deviations in the fitting and prediction of confirmed cases. Secondly, the parameters within these models play a critical role in determining prediction outcomes. Setting default parameters based on existing knowledge and subjective judgment can lead to discrepancies in results, especially in scenarios with limited data.Furthermore, many models overlook the classification and analysis of different types of quarantined cases, which may not align with effective epidemic control policies and the unique transmission characteristics of Covid-19. This oversight can result in suboptimal prediction accuracy and other challenges.

To address these limitations, we developed a novel SQEAIR model that considers both quarantine policies and the presence of asymptomatic cases. This model categorizes quarantined individuals into exposed, asymptomatic, and infected groups. By incorporating these compartments and simulating contact tracing, isolation protocols, and the release of asymptomatic cases based on medical observation, the SQEAIR model offers a more comprehensive approach to epidemic prevention and control. The model also accounts for isolating exposed and asymptomatic cases, leading to improved predictive accuracy compared to the traditional SEIR model.Through parameter optimization and fitting the model to the number of infected cases, we demonstrated the superior performance of the SQEAIR model. Finally, by testing various parameterizations, we evaluated the effectiveness of epidemic control measures implemented by governments, health authorities, and individuals in curbing the spread of Covid-19.

2 Model Introduction

The most widely used infectious disease dynamics modeling methods are grouped as compartment model, and a prominent one, namely the SEIR model. It was established by Kermack WO and McKendrick AG [21] in 1927 when studying the Black Death in London and the plague in Mumbai, which was developed into a specialized theory: infectious disease dynamics. These models describe the transmission process of infectious diseases, analyze the change rule of the number of infected individuals, and reveal the development pattern of infectious diseases through the quantitative relationship according to the general infectious disease transmission mechanism [22].

2.1 SEIR Model

In the SEIR model, the following assumptions are made:

  1. 1.

    The total population of the region remained unchanged during the disease observation period;

  2. 2.

    Each individual is equally likely to be infected, and only person-to-person transmission is considered;

  3. 3.

    After treatment and recovery, cases will not be transformed into susceptible cases in a short time.

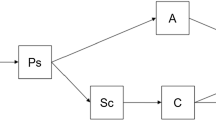
SEIR model divides the total population into the following categories:

Susceptible (S): those who are not infected but have a chance of contracting the disease;

Exposed (E): refers to individuals who are in the incubation period and will become infected after the incubation period;

Infected (I): refers to individuals who are infectious and are showing symptoms;

Removed (R): refers to individuals who have either recovered or died among the infected individuals;

The model flow chart is as follows:

Fig. 1
figure 1

Flow chart of SEIR infectious disease dynamics model

Full size image

\(\beta \) is the effective contact rate of cases per unit time, \(\omega \) is the probability of converting a exposed person into an infected person, and \(\gamma \) is the probability of recovery or death of cases (Fig. 1).

Based on the SEIR infectious disease dynamics model and the above assumptions, differential equations can be constructed:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dS}{dt}=-\frac{{\beta }SI}{N} \\&\frac{dE}{dt}=\frac{{\beta }SI}{N}-{\omega }E \\&\frac{dI}{dt}={\omega }E-{\gamma }I \\&\frac{dR}{dt}={\gamma }I \\ \end{aligned} \right. \end{aligned}$$
(1)

2.2 Improved SQEAIR Model

On the basis of the traditional SEIR model, we propose the SQEAIR infectious disease dynamics model by considering the characteristics of the transmission of the novel coronavirus pneumonia and China’s epidemic prevention policies.

In SQEAIR model, the following assumptions are added:

  1. 1.

    The quarantined cases include some of the close contacts of exposed cases, asymptomatic cases and infected cases, and the quarantined cases will not infect others;

  2. 2.

    Latent cases are tested to have been affected (confirmed) or asymptomatic cases after the incubation period;

  3. 3.

    Latent, asymptomatic, and confirmed cases are all infectious, and the infection rate is the same;

  4. 4.

    Confirmed cases and asymptomatic cases were treated and eventually cured or died.

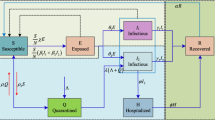
SQEAIR model is proposed on the basis of the traditional SEIR model, and the following four compartments are added for research:

Asymptomatic cases (A): cases who are infected but not showing symptoms;

Quarantined exposed cases (\(Q_{E}\)): cases who are exposed but not capable of infecting susceptible cases;

Quarantined asymptomatic cases (\(Q_{A}\)): cases who are asymptomatic but not capable of infecting susceptible cases;

Quarantined infected cases (\(Q_{I}\)): cases who are infected and not capable of infecting susceptible cases;

The model flow chart is as follows:

Fig. 2
figure 2

Flow chart of dynamic model of SQEIAR infectious disease

Full size image

The effective contact rate per unit of time of a patient is \(\beta \). When a susceptible individual is infected, they initially enter the incubation period or a latent state, with the rate of conversion from a latent individual to an infected individual denoted as \(\omega \). Infected individuals encompass both asymptomatic cases and diagnosed patients. The proportion of infected individuals who exhibit symptoms and progress to confirmed patients is p, while the proportion of asymptomatic infected individuals who remain symptom-free is \(1-p\). The rate at which an asymptomatic infected individual transitions to a confirmed patient is \(\delta \).

Individuals have a likelihood of entering the isolation category during the latent, asymptomatic infected, and confirmed patient phases, with the respective proportions denoted as q, \(\lambda \) , \(\mu \).

Individuals admitted to the isolation category remain there until they recover or pass away, becoming emigrants. \(\gamma _{1}\) represents the rate that the confirmed but not quarantined patients recover or pass away, \(\gamma _{2}\) represents the rate that asymptomatic infected but not quarantined ones recover or pass away, \(\gamma _{3}\) represents the rate that the quarantined and treated ones recover or pass away, and \(\gamma _{4}\) represents the rate that the quarantined asymptomatic infected ones recover or pass away (Fig. 2).

Based on the SQEAIR model and the above assumptions, differential equations can be constructed:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dS}{dt}=-\frac{{\beta }S(E+A+I)}{N} \\&\frac{dE}{dt}=\frac{{\beta }S(E+A+I)}{N}-{[(1-q)\omega +q]}E \\&\frac{d{Q_E}}{dt}=qE-{\omega }{Q_E} \\&\frac{dA}{dt}=(1-q)(1-p){\omega }E-({\lambda }+{\delta }+{\gamma _{2}})A \\&\frac{d{Q_A}}{dt}=(1-p){\omega }{Q_E}+{\lambda }A-({\delta }+{\gamma _{4}}){Q_A} \\&\frac{dI}{dt}=(1-q)p{\omega }E+{\delta }A-({\mu }+{\gamma _{1}})I \\&\frac{d{Q_I}}{dt}=p{\omega }{Q_E}+{\delta }{Q_A}+{\mu }I-{\gamma _{3}}{Q_I} \\&\frac{dR}{dt}={\gamma _{1}}I+{\gamma _{2}}A+{\gamma _{3}}{Q_I}+{\gamma _{4}}{Q_A} \\ \end{aligned} \right. \end{aligned}$$
(2)
Table 1 The situation in Shanghai, Mar. 28, 2022
Full size table

Since the effective contact rate of patients per unit time \(\beta \) will continue to decrease with the increase and decrease of prevention and control measures and monitoring efforts, this paper describes the change of effective contact rate of patients per unit time \(\beta \) over time by introducing inhibitory factors:

$$\begin{aligned} {\beta (t)}={\beta _{0}}{e^{-{\alpha }}} \end{aligned}$$
(3)

Where \(\alpha \) denotes the exponential decreasing rate of effective contact rate \(\beta \), which is used to indicate the inhibiting effect of epidemic prevention work on the spread of the epidemic, and \(\beta _{0}\) denotes the initial value of the effective contact rate, and the effective contact rate on the first day of the experimental data is used as the initial value of the effective contact rate, which can be introduced according to the first differential equation above:

$$\begin{aligned} {\beta _{0}}=\frac{({S_{0}}-{S_{1}})N}{{S_{0}}({E_{0}}+{A_{0}}+{I_{0}})} \end{aligned}$$
(4)

Therefore, both \(\beta \) in the system of Eq. 2 are: \(\frac{({S_{0}}-{S_{1}})N}{{S_{0}}({E_{0}}+{A_{0}}+{I_{0}})}\)

2.3 Model Solving

Runge-Kutta Method is an important iterative method for solving nonlinear ordinary differential equations, it can be used to solve the SEIR model and SQEAIR model. This method is mainly used when the derivative and initial value information of the equation are known and computer simulation is used, which can save the complicated process of solving the differential equation. In the following, the SEIR model is taken as an example to introduce the solution process of Runge-Kutta Method.

First, the time interval [0, t] is discretized into n step, each of which is \(h=\frac{t}{n}\) .

Second, initialize initial conditions: \(S_0\), \(E_0\), \(I_0\), \(R_0\) (the meaning of the arguments are shown in Table 1).

Third, for each time step, calculate the \(k_1\) of the current time step:

$$\begin{aligned} \left\{ \begin{aligned}&{k_{1S}}=-\frac{{\beta }{S_n}{I_N}}{N} \\&{k_{1E}}=\frac{{\beta }{S_n}{I_N}}{N}-{\omega }{E_n} \\&{k_{1I}}={\omega }{E_n}-{\gamma }{I_n} \\&{k_{1R}}={\gamma }{I_n} \\ \end{aligned} \right. \end{aligned}$$
(5)

calculate the \(k_2\) of the current time step:

$$\begin{aligned} \left\{ \begin{aligned}&{k_{2S}}=-\frac{{\beta }({S_n}+\frac{h}{2}{k_{1S}})({I_N}+\frac{h}{2}{k_{1I}})}{N} \\&{k_{2E}}=\frac{{\beta }({S_n}+\frac{h}{2}{k_{1S}})({I_N}+\frac{h}{2}{k_{1I}})}{N}-{\omega }({E_n}+\frac{h}{2}{k_{1E}}) \\&{k_{2I}}={\omega }({E_n}+\frac{h}{2}{k_{1E}})-{\gamma }({I_n}+\frac{h}{2}{k_{1I}}) \\&{k_{2R}}={\gamma }({I_n}+\frac{h}{2}{k_{1I}}) \\ \end{aligned} \right. \end{aligned}$$
(6)

calculate the \(k_3\) of the current time step:

$$\begin{aligned} \left\{ \begin{aligned}&{k_{3S}}=-\frac{{\beta }({S_n}+\frac{h}{2}{k_{2S}})({I_n}+\frac{h}{2}{k_{2I}})}{N} \\&{k_{3E}}=\frac{{\beta }({S_n}+\frac{h}{2}{k_{2S}})({I_n}+\frac{h}{2}{k_{2I}})}{N}-{\omega }({E_n}+\frac{h}{2}{k_{2E}}) \\&{k_{3I}}={\omega }({E_n}+\frac{h}{2}{k_{2E}})-{\gamma }({I_n}+\frac{h}{2}{k_{2I}}) \\&{k_{3R}}={\gamma }({I_n}+\frac{h}{2}{k_{2I}}) \\ \end{aligned} \right. \end{aligned}$$
(7)

calculate the \(k_4\) of the current time step:

$$\begin{aligned} \left\{ \begin{aligned}&{k_{4S}}=-\frac{{\beta }({S_n}+h{k_{3S}})({I_n}+h{k_{3I}})}{N} \\&{k_{4E}}=\frac{{\beta }({S_n}+h{k_{3S}})({I_n}+h{k_{3I}})}{N}-{\omega }({E_n}+h{k_{3E}}) \\&{k_{4I}}={\omega }({E_n}+h{k_{3E}})-{\gamma }({I_n}+h{k_{3I}}) \\&{k_{4R}}={\gamma }({I_n}+h{k_{3I}}) \\ \end{aligned} \right. \end{aligned}$$
(8)

Thus, the next value is determined by the product of the present values, the time interval (h), and a slope estimated by the weighted average of the slopes of \(k_1\), \(k_2\), \(k_3\), and \(k_4\), where \(k_1\) is the slope at the beginning of the time period; \(k_2\) is the slope of the midpoint of the time period, and the slope \(k_1\) is used to determine the value of y. \(k_3\) is also the slope of the midpoint, and the slope \(k_2\) is used to determine y. \(k_4\) is the slope of the end point of the time period, whose y is determined by \(k_3\). When the four slopes are averaged, the slope of the midpoint has a greater weight. The Runge-Kutta method for SEIR model is given by the following equation:

$$\begin{aligned} \left\{ \begin{aligned}&{S_{n+1}}={S_n}+\frac{h}{6}({k_{1S}}+2{k_{2S}}+2{k_{3S}}+{k_{4S}}) \\&{E_{n+1}}={E_n}+\frac{h}{6}({k_{1E}}+2{k_{2E}}+2{k_{3E}}+{k_{4E}}) \\&{I_{n+1}}={I_n}+\frac{h}{6}({k_{1I}}+2{k_{2I}}+2{k_{3I}}+{k_{4I}}) \\&{R_{n+1}}={R_n}+\frac{h}{6}({k_{1R}}+2{k_{2R}}+2{k_{3R}}+{k_{4R}}) \\ \end{aligned} \right. \end{aligned}$$
(9)

Through several iterations, the approximate values of each time step S, E, I, R, can be obtained to solve the SEIR model. Using the same method, arguments in the SQEAIR model can also be solved.

In this paper, the 4-order Runge-Kutta Method is used to solve the differential equation. The 5-order method controls the error, and the overall truncation error is \(\circ (h^5)\).

2.4 Basic Reproduction Number

Basic reproduction number, usually denoted by \(R_0\), it is an important indicator in epidemiology of the ability of an infectious disease to spread in a given population. The basic regeneration number indicates the average number of susceptible individuals in a population who develop the disease per infected individual during the infectious period. When \({R_0}>1\), it indicates that an infected person transmits the virus to more than one newly infected individual during their illness. Consequently, the number of people afflicted with the disease increases, and the disease persists. Conversely, when \({R_0}<1\), the infected person transmits the virus to fewer than one newly infected individual throughout the course of the disease. As a result, the number of people suffering from the disease decreases, and the disease is gradually eradicated. When \({R_0}=1\), the number of people suffering from the disease will be constant.

Van den Driessche P [23] gave an exact procedure for the computation of the fundamental regeneration number \(R_0\) based on the propagation of a system of ordinary differential equations for hamster models, which has been widely used, as follows:

Let \(x={({x_1},{x_2},\cdots ,{x_n})}^T\), where \({x_i}\ge 0(i=1,2,\cdots ,n)\), denotes the number of individuals in the i, compartment. Let \({F_i}(x)\) be the probability of a new infection in the i compartment, \(V_{i}^{+}(x)\) be the rate of movement of individuals into the i compartment, and \(V_{i}^{-}(x)\) be the rate of movement of individuals out of the i compartment. Assuming that each function is continuously differentiable at least twice in each variable, the disease transmission model consists of non-negative initial conditions and the following equations:

$$\begin{aligned} \frac{dS}{dt}={F_i}(x)-{V_i}(x),i=1,2,\cdots ,n \end{aligned}$$
(10)

where \({V_i}(x)={V_{i}^{+}(x)}-{V_{i}^{-}(x)}\)? \({V_{i}^{-}(x)}\) denotes the rate of individuals moving out of the i compartment, \({V_{i}^{+}(x)}\) denotes the rate of individuals moving into the i compartment, and \({F_i}(x)\) denotes the rate of new infections.

Calculate the full derivatives of \({F_i}(x)\) and \({V_i}(x)\) with respect to \(x={({x_1},{x_2},\cdots ,{x_n})}^T\) respectively, the full derivative of \({F_i}(x)\) is \(F=[\frac{\partial {F_i}}{\partial {x_i}}(x_0)]\) and the full derivative of \({V_i}(x)\) is \(V=[\frac{\partial {V_i}}{\partial {x_i}}(x_0)]\), where \({x_0}\) denotes the disease-free equilibrium point.

The formula for the basic regeneration number \(R_0\) is obtained:

$$\begin{aligned} R_0=\rho (FV^{-1}) \end{aligned}$$
(11)

Here, \(V^{-1}\) denotes the inverse matrix of matrix V, and \(\rho (FV^{-1})\) denotes the spectral radius of matrix \(FV^{-1}\), i.e.,the upper definitive bound on the absolute value of the eigenvalues of the matrix.

Since in the SQEAIR model, only three bins, E, A, and I, are infected, only the following new system consisting of the second, fourth, and sixth equations needs to be utilized to calculate the basic regeneration number:

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dE}{dt}=\frac{{\beta }S(E+A+I)}{N}-{[(1-q)\omega +q]}E \\&\frac{dA}{dt}=(1-q)(1-p){\omega }E-({\lambda }+{\delta }+{\gamma _{2}})A \\&\frac{dI}{dt}=(1-q)p{\omega }E+{\delta }A-({\mu }+{\gamma _{1}})I \\ \end{aligned} \right. \end{aligned}$$
(12)

Let \(x={(E,A,I)}^T\), then the above system of ordinary differential equations can be written as \(\frac{dx}{dt}=F(x)-V(x)\), where:

$${F(x)}=\left[ \begin{array}{cc} \frac{{\beta }S(E+A+I)}{N} \\ 0 \\ 0 \\ \end{array} \right] .$$
$${V(x)}=\left[ \begin{array}{cc} [(1-q){\omega }+q]E \\ -(1-q)(1-p){\omega }E+({\lambda }+{\delta }+{\gamma _{2}}) \\ -(1-q)p{\omega }E-{\delta }A+({\mu }+{\gamma _{1}})I \\ \end{array} \right] .$$

Calculating the full derivatives of F(x) and V(x) with respect to \(x={(E,A,I)}^T\), respectively, yields:

$${F}=\left[ \begin{array}{ccc} \frac{{\beta }S}{N} &{} \frac{{\beta }S}{N} &{} \frac{{\beta }S}{N} \\ 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \end{array} \right] .$$
$${V}=\left[ \begin{array}{ccc} [(1-q){\omega }+q] &{} 0 &{} 0 \\ -(1-q)(1-p){\omega } &{} {\lambda }+{\delta }+{\gamma _{2}} &{} 0 \\ -(1-q)p{\omega } &{} {\delta } &{} {\mu }+{\gamma _{1}} \\ \end{array} \right] .$$

from Eq. 11:

$$\begin{aligned} R_0=\frac{\beta }{(1-q){\omega }+q}[1+\frac{(1-q)(1-p){\omega }}{{\lambda }+{\delta }+{\gamma _{2}}}+\frac{(1-q)p{\omega }}{{\mu }+{\gamma _{1}}}+\frac{(1-q)(1-p){\omega }{\delta }}{({\lambda }+{\delta }+{\gamma _{2}})({\mu }+{\gamma _{1}})}] \end{aligned}$$
(13)

Since \({\beta }={{\beta }_0}e^{-{\alpha }t}\), the expression for the fundamental regeneration number \(R_0\) is

$$\begin{aligned} R_0=\frac{{{\beta }_0}e^{-{\alpha }t}}{(1-q){\omega }+q}[1+\frac{(1-q)(1-p){\omega }}{{\lambda }+{\delta }+{\gamma _{2}}}+\frac{(1-q)p{\omega }}{{\mu }+{\gamma _{1}}}+\frac{(1-q)(1-p){\omega }{\delta }}{({\lambda }+{\delta }+{\gamma _{2}})({\mu }+{\gamma _{1}})}] \end{aligned}$$
(14)

2.5 Evaluating Indicators

For the prediction of the number of existing infected cases and model selection, Akaike information criterion (AIC) is adopted to test the accuracy of the two models. AIC was proposed by Akaike H [24] in 1974. It measures the quality of relative statistical models, based on reducing information dissipation. In addition, it can help determine the best model, thereby reducing model overfitting and improving model accuracy. Its prominet advantage is that it can obtain more accurate results through the gain of parameters or the reduction of information dissipation in the selection of models.

The specific formula are as follows:

$$\begin{aligned} AIC=2p+n\ln \frac{RSS}{n} \end{aligned}$$
(15)
$$\begin{aligned} RSS=\sum _{i=1}^{n}{({y_i}-\hat{y_i})^2} \end{aligned}$$
(16)

where n is the observed number, RSS is residual sum of squares, p is the number of parameters, \(y_i\) is the actual number of infected cases, and \(\hat{y_i}\) is the observed number of infected cases.

To further assess the prediction effectiveness of the number of existing infected cases, Mean Absolute Percentage Error (MAE), Mean Squared Error (MSE), Root Mean Squared Error (RMSE), and Mean Absolute Percentage Error (MAPE) are also used to test the accuracy of the two models. The specific formula are as follows:

$$\begin{aligned} MAE(y,{\hat{y}})=\frac{1}{n}\sum _{i=1}^{n}|{y_i}-{\hat{y_i}}| \end{aligned}$$
(17)
$$\begin{aligned} MSE(y,{\hat{y}})=\frac{1}{n}\sum _{i=1}^{n}{({y_i}-{\hat{y_i}})^2} \end{aligned}$$
(18)
$$\begin{aligned} RMSE(y,{\hat{y}})=\sqrt{\frac{1}{n}\sum _{i=1}^{n}{({y_i}-{\hat{y_i}})^2}} \end{aligned}$$
(19)
$$\begin{aligned} MAPE(y,{\hat{y}})=\frac{1}{n}\sum _{i=1}^{n}|\frac{{y_i}-{\hat{y_i}}}{y_i}| \end{aligned}$$
(20)

3 Numerical Simulation and Prediction

3.1 Numerical Simulation and Model Comparison

Since the outbreak of the epidemic, the National Health Commission of the People’s Republic of China (NHC) has reported data on a daily basis, including the number of new confirmed cases, the number of new asymptomatic cases, the number of asymptomatic cases converted to confirmed cases, the number of newly cured asymptomatic cases removed from medical observation, the number of existing confirmed cases, the number of asymptomatic cases, and the number of cases quarantined. We retrieved epidemic-related data from Shanghai, China for 65 days from March 28 to May 31, 2022, as well as data related to the model such as population of shanghai. The preliminary values of cases groups are shown in Table 1, with official data from NHC, exposed at the beginning is on the basis of the rate of exposed cases transforming into infected cases to estimate, the actual data of infected cases and asymptomatic cases are shown in Fig. 3.

Fig. 3
figure 3

Infected and asymptomatic cases in Shanghai

Full size image

After obtaining the data, we first conducted stationarity test on the original data. Augmented Dickey-Fuller (ADF) test is also called the unit root test. The ADF test is to determine whether the sequence has a unit root: if the sequence is stationary, there is no unit root; Otherwise, there will be a unit root. Therefore, the null hypothesis of ADF test is the existence of unit root. If the obtained significance test statistic is less than 0.05, there is no unit root, and the sequence is stable. The ADF test values of both the existing confirmed cases and the existing asymptomatic cases were less than 0.05, negating the null hypothesis and believing that the original sequence was stable. Secondly, white noise test was carried out on the original data. The p value of the existing confirmed cases was \(9.992\times 10^{-6}\) and the value of the existing asymptomatic cases was \(1.221\times 10^{-15}\), indicating that neither of the two groups of original data was white noise and could reflect the real trend and rule of the time series.

As to the data collected above, MATLAB software was used to conduct numerical simulation for the number of existing infections (number of existing infections are equal to the cumulative number of confirmed minus cumulative number of removed), and the values of parameters in the model (Table 2), the values of evaluating indicators (Table 3), and the fitting curve (Figs. 4 and 5) were obtained.

Table 2 Model parameters for Shanghai
Full size table

As to the fitting results (Figs. 4 and 5) and the AIC evaluation indexes (Table 3), although the improved SQEAIR model has four more chambers and added parameters than the original SEIR model, the fitting value is closer to the real data, the error is relatively low, and the fitting accuracy has improved, with better fitting effect. Notably, the fitting effect of SEIR model is accurate in the early stage, the estimated value in the middle stage is slightly lower than the real value, while the estimated value in the later stage is higher than the real value. Thus, the SQEAIR model is more suitable for the prediction of the number of cases infected by the Covid-19 epidemic in Shanghai.

In order to test the accuracy of the model, we also collected 32 days of epidemic data in Guangzhou, China, from November 1 to December 2, 2022 on the official website of Guangzhou Health Commission (Table 4). The actual data of the existing asymptomatic number, the existing confirmed number, the cumulative confirmed number, and the cumulative cured number are shown in Fig. 6.

Table 3 Evaluating indicators of the models
Full size table
Fig. 4
figure 4

The fitting results of SQEAIR model

Full size image
Fig. 5
figure 5

The fitting results of SEIR model

Full size image

The accuracy of SQEAIR model is verified again by comparing the fitting effect diagram and the error evaluation index (Figs. 7 and 8).

In addition, SQEAIR model can also fit and predict the number of asymptomatic cases because of the addition of asymptomatic cases compartment. Figure 9 shows the fitting results of SQEAIR model on the number of asymptomatic cases in the epidemic in Shanghai. It can be seen that the overall fitting effect is good, and the specific error indicators are shown in Tables 3, 5 and 6.

Table 4 The situation in Guangzhou, Nov. 1, 2022
Full size table

3.2 Prediction

Based on the SQEAIR model with high accuracy and the estimated values of the parameters obtained above, the future development trend of the epidemic in Guangzhou was predicted, and the prediction results were obtained on December 3 and in the following five days (Table 7) and the prediction effect diagram (Fig. 10). As shown in Table 7 and Fig. 10, the predicted number of cases is not much different from the real number of cases, average error rate is \(2.93\%\), the overall prediction effect is relatively good, indicating that the parameter estimation is relatively accurate, and the SQEAIR model can simulate the development law of the epidemic situation well. Besides the number of confirmed cases in Guangzhou will gradually rise in the next five days, but has been actually kept within a manageable range.

Fig. 6
figure 6

Infected and asymptomatic cases in Guangzhou

Full size image
Fig. 7
figure 7

The fitting results of SQEAIR model

Full size image
Fig. 8
figure 8

The fitting results of SEIR model

Full size image

The basic regeneration number \(R_0\) is a key indicator for portraying whether there is an outbreak of an infectious disease, so it is necessary to utilize the calculations of the epidemic data from Guangzhou City to determine whether there is a possibility of a large-scale outbreak.

The SQEAIR model was utilized to fit the number of existing infections in Guangzhou City, and the values of each parameter were obtained as shown in the Table 8.

Fig. 9
figure 9

SQEAIR model was used to fit the number of asymptomatic cases in the Shanghai

Full size image

According to the formula and the values of the parameters in the above table, the transformed graph of the basic regeneration number can be obtained (Fig. 11).

Since the beginning of the Guangzhou epidemic on November 1, the value of the basic regeneration number is 2.06, and then it gradually decreases. In fact, the basic regeneration number \({R_0}=1\) on the 17th day, and then the values become smaller than 1, which means that from the 17th day onwards, on average, each infected person causes fewer than 1 person to be infected of the disease during, meaning that the disease’s infectious capacity has begun to decline. Due to the incubation period and the time required for asymptomatic infected persons to turn into confirmed patients, the epidemic will eventually be brought under control, although the number of infected persons is still gradually increasing.

4 Influencing Factors

Based on the SQEAIR model proposed above, respectively considering the impact of tracking isolation measures, medical treatment level and personal protection measures on the number of infected cases, and the effect of prevention and control was evaluated by changing parameters. The effectiveness of prevention and control strategies was evaluated mainly by the number of cases and the peak of the epidemic. The following prediction assumes a local population of 100,000.

Table 5 Evaluating indicators of the models
Full size table
Table 6 Evaluating indicators of the models
Full size table

4.1 Tracking Quarantine Measures

Local epidemic prevention authorities implemented control measures for close contacts and sub-close contacts, reflecting the effectiveness of the government?s tracking and quarantine measures. Scientific tracking quarantine measures can reduce the rate of infection effectively. Here, we depict the impact of different quarantined rate of exposed cases on the number of cases who got sick in an outbreak (Fig. 12). When the quarantined rate of exposed cases is 0, the number of asymptomatic cases and confirmed cases would greatly increase, and the peak of the epidemic would come in advance, which would have a great impact on local medical supplies and production and life. When the quarantined rate of exposed cases increases, the number of asymptomatic cases and confirmed cases would be significantly reduced, the peak of the epidemic would come later, and the impact on local medical institutions would be greatly reduced (Table 9).

4.2 Medical and Health Level

Local cure rates of infected cases reflecting the effectiveness of the Medical and health level. Figures 13 and 14 depicts the impact of the recovery rate of different infected cases on the number of sick cases in the epidemic. When medical and health level is inferior, the number of asymptomatic cases and confirmed cases will increase greatly, and the peak of the epidemic will come in advance, which will have a great impact on local medical supplies and production and life. When the medical level is high, the number of asymptomatic cases and confirmed cases will be significantly reduced, the peak of the epidemic will come later, and the impact on local medical institutions will be greatly reduced. And with the improvement of medical level, the peak number of infected cases decreased significantly (Tables 10 and 11).

Table 7 Evaluating indicators of the models
Full size table
Fig. 10
figure 10

Prediction results of SQEAIR model

Full size image
Table 8 Model parameters for Guangzhou
Full size table

4.3 Personal Protection Measures

Individual epidemic prevention behaviors, such as wearing masks when going out, washing hands frequently at home, and using public spoons and chopsticks, reflect citizens’ attention to the Covid-19 epidemic, and scientific protective measures can effectively reduce the rate of infection. The figure below depicts the effect of different effective exposure rates on the number of cases in an outbreak. As can be seen from the Fig. 15, the lower the effective contact rate of cases, the smaller the number of asymptomatic infected and confirmed cases, and the later the peak of the epidemic, the more conducive to the control of the epidemic. And with the reduction of the effective contact rate of cases, the peak number of infected cases has been significantly reduced (Table 12)

5 Conclusion

This study focuses on fitting, predicting, and scientifically managing the number of infected individuals using an enhanced infectious disease dynamics model tailored to the specific circumstances of the epidemic in China. Initially, an improved SQEAIR infectious disease dynamics model was developed by augmenting the traditional SEIR model with three isolation compartments and one asymptomatic infected compartment to create a more realistic representation.

Fig. 11
figure 11

Basic regeneration number change curve

Full size image
Fig. 12
figure 12

The impact of quarantine measures on the number of cases infected in the outbreak

Full size image
Table 9 Table of epidemic peaks corresponding to different quarantined rate of exposed cases
Full size table
Fig. 13
figure 13

Influence of cure rates of infected cases on the numbers of infected cases in the outbreak

Full size image
Fig. 14
figure 14

Influence of cure rates of asymptomatic cases on the numbers of infected cases in the outbreak

Full size image

Subsequently, data pertaining to the number of infected individuals in Shanghai, China, between March and May 2022 were gathered and fitted using both the SEIR and SQEAIR models. The estimates of crucial parameters in the models and the associated error values were then calculated. The results indicated that the SQEAIR model exhibited a lower fitting error and a reduced AIC value, suggesting its superior fit compared to the traditional infectious disease dynamics model in capturing the epidemic trend in Shanghai. Moreover, when the SQEAIR model was applied to fit data on asymptomatic infected individuals in Shanghai, the error rate was notably lower at 6.5%.

To further validate the model’s accuracy, data on infected individuals in Guangzhou City in November 2022 were collected, with results consistently favoring the SQEAIR model over the SEIR model. Subsequent predictions using the improved model for confirmed cases in Guangzhou over the next five days yielded a low prediction error of only 2.53%. Calculations of the basic reproduction number of the epidemic in Guangzhou indicated that it had already reached 1 and was gradually decreasing, suggesting that while confirmed cases might rise, they would remain manageable.

Table 10 Epidemic peaks corresponding to the cure rates of different infected cases
Full size table
Table 11 Epidemic peaks corresponding to the cure rates of different asymptomatic cases
Full size table
Fig. 15
figure 15

Impact of personal protection measures on the numbers of cases infected in an outbreak

Full size image
Table 12 Table of epidemic peaks corresponding to different effective contact rates
Full size table

Finally, leveraging the enhanced SQEAIR infectious disease dynamics model, the study explored the impact of varying latent isolation rates, infected person recovery rates, and effective patient contact rates on the number of infected individuals. Simulation results highlighted that higher isolation rates, lower recovery rates, and reduced patient contact rates led to fewer infections and delayed epidemic peaks, underscoring the importance of effective public management in outbreak prevention and control efforts.