1 Introduction

The wings as important parts of the aircraft play a crucial role in flight, such as providing lift, bearing load, controlling direction as well as keeping the stability of flying. During flight, each section of the wings under external loads is subjected to shear force, bending moment and torque. When the aircraft reaches a certain speed or is disturbed by turbulence, the wing, tail and control surface of the aircraft will produce flutter. Flutter is a kind of self-excited vibration, which is a negative damping motion phenomenon of the structure in the air flow due to the fluid–structure coupling. When wings vibrate or buffet, in addition to elastic force and aerodynamic force, there are also the inertia forces whose magnitude and direction change with time. In this case, the phase difference between the instantaneous aerodynamic force and the elastic displacement on the structure will be generated. Therefore, the vibration structure will lose its dynamic stability when it draws energy from the air flow, resulting in flutter or buffeting of the wing [1]. Once the structure vibrates beyond some critical amplitude, the wings will be damaged in a very short time or even a few seconds, which is prone to catastrophic accidents. In engineering practice, flutter must be avoided either by design of the structure or by introducing a control mechanism capable of suppressing harmful vibrations [2].

When the structural stiffness is insufficient, the dynamic aeroelasticity of wings may occur in the range of flight speed, and in this case the stiffness criterion is the critical speed at which aeroelastic phenomena occur. Because of the high risk, high cost and long cycle of flutter test flight, the flutter envelope is usually difficult to obtain directly from the test. Therefore, the determination of flutter boundary and critical flutter speed of the wing is the premise of safe flight of aircraft. An accurate flutter prediction capability in theory would reduce significantly the number of flights required in any flight clearance test programme [3]. In addition, increasing the torsional stiffness of wings, making the center of gravity move forward and the twist move back as well as regulating the shape of the wing section are also conducive to inhibiting the early occurrence of flutter. Therefore, it is important to consider the influence of many factors and parameters on flutter amplitude of the wing. And many researchers have investigated the static instability and subsequent dynamics phenomena of wings from different perspectives.

Based on numerical continuation techniques, a nonlinear reduced-order beam model combined with strip theory has been investigated in [4]. The effect of varying parameters corresponding to the bending stiffness, the torsional stiffness and the coupling factor has been investigated via two-parameter continuation of Hopf points and periodic folds. It is shown that the dynamics of the wing is sensitive to the variation of these parameters. In [5] a data-driven method is utilized to forecast the bifurcation behavior of a geometrically nonlinear wing, where postflutter responses can be efficiently forecast based on a few system transient computations in the pre-flutter regime. Subcritical bifurcations, period-doubling and nontypical bifurcations have been observed for an aeroelastic half-span Delta wing system in a low speed wind tunnel in [6]. It is shown that the limit cycle oscillations (LCOs) resulting from the nontypical bifurcation display Hopf-type behavior with fundamental frequencies equal to one of the linear modal frequencies. While the other LCOs have fundamental frequencies that are unrelated to the underlying linear system modes.

Irani et al. [7] have calculated the oscillation frequency and amplitude of the limit cycle for a swept aircraft wing based on the harmonic balance method. It is concluded that the bifurcation type and turning point location is sensitive to the system parameters such as wing geometry and sweep angle. The nonlinear dynamical characteristics of a Z-shaped folding wing has been investigated during the morphing process in paper [8]. The method of multiple scales is employed to obtain the averaged equations of the system. It is shown that the system has performed periodic and chaotic motions and 1:1 inner resonance under given conditions. Zhang et al. [9] have investigated the dynamics of a two-dimensional wing encountering a wind gust on account of the indicial aerodynamic theory based on Wagner’s function. With two different types of stiffness nonlinearities, bifurcation diagrams, power-spectral density, phase-plane and Poincar\(\acute{\text {e}}\) diagrams are presented at different flow velocities. It is shown that the system with the free-play nonlinearity performs complexity of occurrence of chaos through period-doubling bifurcations. While the dynamics with the hysteresis nonlinearity is found to be rather simple.

Wang et al. [10] utilize the differential transformation method to examine the nonlinear dynamic response of an aircraft wing. Bifurcation diagrams, Poincaré maps, power spectra and maximum Lyapunov exponent plots reveal that there exist complex dynamic behaviors comprising periodic, quasi-periodic and chaotic responses and chaotic motion occurs at specific intervals for different trailing edge and leading edge angles. An aeroelastic system with translational and rotational degrees of freedom has been considered in [11], where evolution of trivial and oblique equilibrium positions is examined and stability criteria are also obtained depending on the system parameters. Limit cycles and their domains of attraction are studied about the flow speed. The effects of cubic nonlinear structural stiffness on the flutter envelope have been investigated in literature [12,13,14,15,16,17], where a supercritical or a subcritical Hopf bifurcation has been discussed based on varying system parameters, initial conditions or degree of nonlinearity. However, it is shown that a cubic polynomial can not be capable to suitably model all the structural nonlinearities. For instance, when the polynomial coefficients are fitted via experimental data, the fifth-order term can not be always neglected [18].

In this paper, we extend the model in [12, 14] by adding fifth-order structurally nonlinear terms on both the pitch and the plunge coordinate and compare the effect of different parameters on the bifurcation structure of equilibria. The stability and bifurcation of trivial and nontrivial equilibria have been investigated by numerical continuation methods with the help of Matcont package.

2 The Equations of Motion of a Wing Model

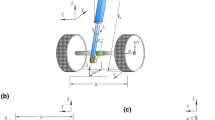
A rigid wing model supported by a higher-order nonlinear spring is exhibited in Fig. 1, where \(E_a\), \(C_m\) and \(M_c\) are the elastic axis, center of mass and semi-chord, respectively.

Fig. 1
figure 1

Sketch of a wing with two-degree-of-freedom pitch and plunge

Full size image

Due to the effect of kinetic and potential energy as well as internal damping and external aerodynamic forces, the motion equations of the wing model are expressed as follows

$$\begin{aligned}&m\ddot{y}+mr\text {cos}(\alpha + \theta )\ddot{\alpha } -mr\text {sin}(\alpha + \theta )\dot{\alpha }^2+C_y\dot{y} +K_y(y + \xi _1y^3 + \xi _2y^5)=-L, \end{aligned}$$
(1)
$$\begin{aligned}&mr\text {cos}(\alpha +\theta )\ddot{y}+I_e\ddot{\alpha } +C_\alpha \dot{\alpha } +K_\alpha (\alpha +\zeta _1 \alpha ^3+\zeta _2\alpha ^5)=M, \end{aligned}$$
(2)
$$\begin{aligned}&L=\pi \rho b^2(\ddot{y}+V\dot{\alpha }-ba\ddot{\alpha }) +C(k)2b\pi \rho V\nonumber \\&\qquad \times \left[ \dot{y}+V\alpha +b\left( \frac{1}{2}-a\right) \dot{\alpha }\right] \triangleq L_{NC}+C(k)L_{Q}, \end{aligned}$$
(3)
$$\begin{aligned}&M=-\pi \rho b^3\left[ -a\ddot{y}+\left( \frac{1}{2}-a\right) V\dot{\alpha } +\left( \frac{1}{8}+a^2\right) b\ddot{\alpha }\right] \nonumber \\&\qquad +2\pi \rho Vb^2C(k)\left( \frac{1}{2}+a\right) \left[ \dot{y}+V\alpha +b\left( \frac{1}{2}-a\right) \dot{\alpha }\right] . \end{aligned}$$
(4)

Wherein y and \(\alpha\) are the plunge and pitch coordinates. L and M represent the unsteady aerodynamic lift and moment, respectively. \(L_Q\) is the quasistatic lift and \(L_{NC}\) is the noncirculatory lift. So the second term in (3) is the circulatory lift \(L_C\), which is affected by the shed-wake induced velocity. C(k) indicates the influence of the shed wake on the aerodynamic loads during unsteady motion [19, 20], which requires to consider a specific time history of the airfoil motion. So the airfoil has been assumed to have purely harmonic motion at frequency \(\omega\). In theory, C(k) is a complex valued Theodorsen’s function of reduced frequency k \((=b\omega /V)\) [21], given by

$$\begin{aligned} C(k)=\frac{H_1^2(k)}{H_1^2(k)+iH_0^2(k)}. \end{aligned}$$

Here \(H_n^2(k)=J_n(k)-iY_n(k)(n=0,1)\) are the Hankel functions of the second kind, where \(J_n(k)\) and \(Y_n(k)\) are the first kind and second kind Bessel function respectively. Due to the complex form of Bessel functions, it is not conducive to analysis development. For the convenience of analysing, here the Theodorsen’s function is replaced by the Theodorsen lift deficiency function \(C(k)=\frac{1}{1+\frac{\pi }{2}k}\) based on the lifting-line approximation [22,23,24] and the degree of approximation has been exhibited in Fig. 2.

The other parameters have been defined and assigned in Table 1, which are derived from the papers [12, 14], where a flutter apparatus as shown in Fig. 3 has been designed to allow motion in two degrees of freedom, and nonlinear pitch and plunge response is introduced through two cams with prescribed nonlinear shapes. The shape of each cam dictates the nature of the nonlinearity. Thus, with this approach, these cams can provide a large family of prescribed responses.

Fig. 2
figure 2

Comparison of the approximate lift deficiency function with the Theodorsen function C(k) [20]

Full size image
Fig. 3
figure 3

A flutter apparatus in [12, 14] performs different nonlinear response in the pitch and plunge degrees of freedom

Full size image

With the change of variables

$$\begin{aligned} y_1=y,~y_2=\dot{y},~y_3=\alpha ,~y_4=\dot{\alpha }, \end{aligned}$$

then Eqs. (1) and (2) combined with expressions (3) and (4) turn into

$$\begin{aligned} \left( \begin{array}{cc} \dot{y}_1\\ \dot{y}_2\\ \dot{y}_3\\ \dot{y}_4\\ \end{array}\right) =\left( \begin{array}{cc} y_2\\ \frac{1}{\delta _1}\left[ 8I_e\delta _2 + 16rm \left( \pi V \rho \delta _4 b^2 - \delta _3\right) \text {cos}(y_3 + \theta ) - \delta _7 + 16b\pi \rho \left( \frac{\delta _2a^2 b^3}{2} + \frac{\delta _2b^3}{16} + a\delta _3b^2 - \delta _6\right) \right] \\ y_4 \\ \frac{1}{\delta _1}\left[ 8mr(mry_4^2\text {sin} (y_3 + \theta ) - 2V\pi b\rho \delta _8 - \delta _2) \text {cos}(y_3 + \theta ) - \delta _9 + 16m\delta _{3} - 16\pi \rho b^2\left( Vm\delta _4 - \frac{ab\delta _2}{2} - \delta _{3}\right) \right] \end{array}\right) , \end{aligned}$$
(5)

where

$$\begin{aligned}{} & {} \delta _1=8m^2r^2\text {cos}^2(y_3 + \theta ) - 16amr\pi \rho b^3\text {cos}(y_3 + \theta ) - \pi ^2\rho ^2 b^6 \\{} & {} \qquad - 8mI_e - 8\pi \rho b^2 \left( ma^2b^2 + \frac{mb^2}{8} + I_e\right) ,\\{} & {} \delta _2=K_y(y_1+\xi _1y_1^3+\xi _2y_1^5)+C_yy_2,\\{} & {} \delta _3=\frac{C_\alpha }{2} y_4 +\frac{K_\alpha }{2}(y_3+\zeta _1y_3^3+\zeta _2y_3^5),\\{} & {} \delta _4=C(k)\left( a+\frac{1}{2}\right) (y_2+Vy_3) -b\left( aC(k)+\frac{1}{2}C(k)-\frac{1}{2}\right) \left( a-\frac{1}{2}\right) y_4,\\{} & {} \delta _5=C(k)\left( a-\frac{1}{4}\right) (y_2+Vy_3) -b\left( C(k)a^2+\frac{ 1}{2}a-\frac{3}{4}aC(k) +\frac{1}{8}C(k)+\frac{1}{8}\right) y_4,\\{} & {} \delta _6=-C(k)VI_e(y_2+Vy_3)+bV I_e \left( a C(k)-\frac{1}{2}C(k)-\frac{1}{2}\right) y_4,\\{} & {} \delta _7=8 V\delta _5 b^5(\pi \rho )^2+rm(8\pi \rho a^2b^4 +\pi \rho b^4+8I_e)y_4^2\text {sin}(y_3 + \theta ),\\{} & {} \delta _8=C(k)y_2+C(k)Vy_3+\left( \frac{1}{2}b-abC(k) +\frac{1}{2}bC(k)\right) y_4,\\{} & {} \delta _9=8\pi \rho mr ab^3\text {sin}(y_3+\theta ) y_4^2 +8V b^4\pi ^2\rho ^2\\{} & {} \qquad \times \left( C(k)y_2+C(k)Vy_3 +\left( \frac{1}{2}bC(k)-abC(k)-\frac{1}{2}b\right) y_4\right) . \end{aligned}$$

3 Stability and Bifurcation of Equilibria

In this section, we will discuss the stability and bifurcation of equilibria. Obviously, the equilibrium \(Y^*=(y_1^*,y_2^*,y_3^*,y_4^*)\) of system (5) should satisfy the following conditions:

$$\begin{aligned} \left\{ \begin{aligned}&y_2^*=y_4^*=0,\\&K_y(8\pi \rho a^2b^4+\pi \rho b^4+8I_e)\left( \xi _2{y_1^*}^5 +\xi _1{y_1^*}^3+{y_1^*}\right) +8 a\pi \rho b^3K_\alpha \left( \zeta _2 {y_3^*}^5+\zeta _1{y_3^*}^3\right) \\&\qquad +2 b\pi \rho \left( \pi \rho C(k) V^2 b^4-4 a \rho \pi C(k) V^2 b^4+8 C(k) I_e V^2+4 a b^2 K_\alpha \right) {y_3^*}\\&\qquad +16rm\left[ -\frac{1}{2}K_\alpha (\zeta _2{y_3^*}^5 +\zeta _1{y_3^*}^3)+\left( a\pi \rho C(k) b^2V^2 +\frac{1}{2}\pi \rho C(k) b^2 V^2-\frac{1}{2} K_\alpha \right) {y_3^*}\right] \\&\qquad \times \cos ({y_3^*}+\theta )=0,\\&8a\pi \rho b^3K_y\left( \xi _2{y_1^*}^5+\xi _1{y_1^*}^3 +{y_1^*}\right) +8K_\alpha (\pi \rho b^2+m) \left( \zeta _2{y_3^*}^5+\zeta _1{y_3^*}^3\right) \\&\qquad -8\left[ C(k)\pi \rho V^2 b^2(\pi \rho b^2+2am+m) -K_\alpha (\pi \rho b^2+m)\right] {y_3^*}\\&\qquad -8 m r\left[ 2\pi \rho b C(k) V^2 {y_3^*} +K_y(\xi _2{y_1^*}^5+\xi _1{y_1^*}^3+{y_1^*})\right] \text {cos}({y_3^*}+\theta )=0. \end{aligned}\right. \end{aligned}$$
(6)

3.1 Effect of V on the Bifurcation of Equilibria

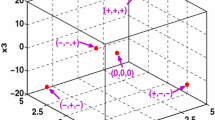
Since the last two equations are transcendental and with too many parameters, it is difficult to obtain their analytical solutions and analyze the structure of equilibria. So the characteristics of equilibria are discussed by the method of numerical simulations. Here V is chosen as a continuation parameter and the other parameters are assigned values as those in Table 1. So the geometrical demonstrations of Eq. (6) are exhibited in three-dimensional space in Fig. 4a and in two-dimensional space in Fig. 4b, respectively. The intersection lines of two surfaces constitute equilibrium curves of the system (5).

Table 1 The coefficients of the rigid wing model
Full size table

Figure 4a, b indicate that the number of equilibria varies from one to three with the increase of the freestream velocity V. The trivial equilibrium O(0, 0, 0, 0) always exists, at which the Jacobian matrix of the system (5) is given as

$$\begin{aligned} A_0=\begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ -1828.4833 &{}\quad -0.4588 V-4.6622 &{} \quad -0.4588 V^2+4.6308 &{}\quad -0.0663 V+0.0144 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 5158.7822 &{}\quad 1.5089V+13.1537 &{} \quad 1.5089V^2-159.4077 &{}\quad -0.0421V-0.4962 \end{pmatrix}. \end{aligned}$$

When V is about less than 26.122 m/s, the eigenvalues of \(A_0\) are all negative and the equilibrium O is locally stable. Two time series about \(y_1\) and \(y_3\) for \(V=25\) m/s have been presented in Fig. 5a. When V is greater than 26.122m/s, the equilibrium O loses its stability and two other stable equilibrium branches bifurcate from the point \((V,y_1,y_3)=(26.122,0,0)\) as shown in Fig. 4a, b.

Since expressions of two additional equilibrium branches are transcendental functions, \(y_1\) and \(y_3\) can not be expressed as explicit functions of V. In order to give the explicit formulations of all the equilibria, the numerical solutions of the nontrivial equilibria have been presented here. Based on the Curve Fitting Toolbox—cftool in Matlab, the nontrivial equilibria can be fitted as polynomial functions of V:

$$\begin{aligned} \left\{ \begin{aligned} y_2^*&=y_4^*=0,\\ y_1^*&=\pm (-0.1936463338\cdot 10^{-2}V^5 +0.2685933142V^4-14.89887497V^3\\&\quad +413.1387911V^2 -5726.974066V+31749.28664),\\ y_3^*&=\pm (0.01037473672V^5-1.440227619V^4 +79.9575446V^3-2219.086013V^2 \\&\quad +30787.76592V-170830.3038), \end{aligned}\right. \end{aligned}$$
(7)

which has been obtained by fitting the intersection points of Fig. 4a or b. The images of Eq. (7) have been presented in Fig. 4c in blue and black curves. The blue curves with pentagrams are corresponding to the expressions with positive signs and the black curves with circles are matching with the expressions with negative signs. The goodness of fit of the points \((V,y_1)\) is: fitting error sum of squares SSE: 8.369\(\cdot 10^{-6}\); coefficient of determination R-square:0.9966; adjusted R-square:0.9955; root mean square error RMSE:0.0007469. The goodness of fit of the points \((V,y_3)\) is: SSE:0.0002828; R-square:0.9975; adjusted R-square:0.9967; RMSE:0.004342. These indices indicate that the graphic of Eq. (7) is a relatively good fit to the intersection lines in Fig. 4b.

Two typical time series graphs for \(V=28\) m/s from different initial values have been displayed in Fig. 5b. It is worth mentioning that the detailed theoretical analysis of stability and bifurcation about the nontrivial equilibria has not been carried out, because the exact explicit expressions of the nontrivial equilibria are unavailable.

A one-parameter bifurcation graph in Fig. 6 further shows that \(V\approx 26.122\) m/s is corresponding to the point BP (\(V=26.12566\) m/s), at which the system undergoes a pitchfork bifurcation and two additional equilibrium branches are bifurcated along with loss of stability of the original equilibrium. Generally speaking, at the branch bifurcation points there will be two kinds of bifurcations to take place. One is the transcritical bifurcation and the other is the pitchfork bifurcation. Bifurcation structure in Fig. 6 corresponds to the latter one.

Fig. 4
figure 4

a The red and the green surface correspond to the second and the third equation in Eq. (5), respectively. b Two-dimensional plots of Fig. 4a in V–\(y_1\) and V–\(y_3\) plane. c The blue curves with pentagrams and the black curves with circles are corresponding to the Eq. (7) with positive signs and negative signs, respectively

Full size image
Fig. 5
figure 5

a Time series of \(y_1\) and \(y_3\) for \(V=25\) m/s. b Two coexistent equilibria for \(V=28\) m/s

Full size image
Fig. 6
figure 6

A one-parameter bifurcation graph in V–\(y_1\) plane. BP —branch point

Full size image

3.2 Effect of \(\xi _2\) and \(\zeta _2\) on the Bifurcation of Equilibria

In this subsection, we will discuss the effect of the coefficients of fifth-order nonlinear terms on the bifurcation structure of equilibria. Here \(\xi _2\) and \(\zeta _2\) have severally been taken as continuation parameters and V is fixed as \(V=30\) m/s as well as the other parameters are fixed as those in Table 1.

For \(\zeta _2=5\), the bifurcation diagrams with \(\xi _2\) as a bifurcation parameter have been displayed in Fig. 7, where the dotted lines represent the unstable trivial equilibrium O and the magenta and blue lines denote the stable nontrivial equilibria. Figure 7 indicates that the parameter \(\xi _2\) does not affect stability and bifurcation structure of all the equilibria, including the trivial and the nontrivial, and furthermore almost has no influence on the position of nontrivial equilibria. That is to say, no matter how the values of \(\xi _2\) vary, the stability and position of all the equilibria remain almost no change.

Fig. 7
figure 7

Bifurcation graphs of the equilibria about parameter \(\xi _2\), where dotted blue lines represent the unstable equilibrium O, and solid blue and magenta lines denote stable nontrivial equilibria

Full size image

For \(\xi _2=50\), if \(\zeta _2\) is regarded as a bifurcation parameter, the bifurcation diagrams about equilibria have been presented in Fig. 8, where LP\(_{1,2}\) with \(\zeta _2=-7.0625\) denote the fold bifurcation points. It is shown that the parameter \(\zeta _2\) does not influence the stability of the origin O, but will affect the position and bifurcation structure of the nontrivial equilibria. When \(\zeta _2<-7.0625\), there only exists one unstable equilibrium O. If \(-7.0625<\zeta _2\), at first, besides the unstable origin O, there also exist two pairs of equilibria with opposite stability. The two lateral branches are stable and the other two longitudinal branches are unstable. As \(\zeta _2\) further increases, the unstable longitudinal branches disappear and only the lateral stable branches has been left besides the origin O.

Remarks

  • In contrast with \(\xi _2\), the effect of \(\zeta _2\) on the bifurcation structure of nontrivial equilibria is relatively prominent.

  • Figures 6 and 7 indicate that if V or \(\xi _2\) act as a bifurcation parameter, two nontrivial equilibria can be produced. While Fig. 8 shows that if \(\zeta _2\) has been taken as a continuation parameter, two pairs of nontrivial equilibria with opposite stability can coexist or disappear by two fold bifurcations. As the parameter \(\zeta _2\) increase further, there only one pair of stable nontrivial equilibria has been left, which dovetails perfectly with the case in Sect. 3.1 for \(\zeta _2=5\).

Fig. 8
figure 8

Bifurcation graphs of the equilibria about the parameter \(\zeta _2\). Dotted lines represent the unstable equilibrium O. Solid blue lines and lines with circles denote stable nontrivial equilibria. Dash lines and dash lines with diamonds signify unstable equilibria

Full size image

4 Stable Parameter Domain of the Equilibrium O

For the equilibrium O, we will discuss how the stable domain varies when the structural spring constants \(K_\alpha\) and \(K_y\) as well as the freestream velocity V are all free. The Jacobian matrix at the point O is given by

$$\begin{aligned} A_1=\begin{pmatrix} 0 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ -0.63866K_y &{}\quad -0.45881V - 4.66222&{}\quad -0.45881V^2 + 1.80188K_\alpha &{}\quad -0.06627V + 0.01442 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 1.80188K_y &{}\quad 1.50887V + 13.15372 &{}\quad 1.50887V^2 - 62.02636K_\alpha &{}\quad -0.04213V - 0.49621 \end{pmatrix}. \end{aligned}$$

Obviously, the characteristic equation of \(A_1\) is deduced as follows

$$\begin{aligned}{} & {} \lambda ^4+(0.50095V+5.15843)\lambda ^3\\{} & {} \quad -(1.38955V^2-1.27401V -62.02636K_\alpha -0.63866K_y-2.12383)\lambda ^2\\{} & {} \quad -(5\cdot 10^{-10}V^3-25.73959VK_\alpha +0.99962V^2-265.47894 K_\alpha \\{} & {} \quad -0.14631K_yV-0.29094K_y)\lambda -0.13693K_yV^2+36.36698K_yK_\alpha =0. \end{aligned}$$

Based on the Hurwitz criterion, stable parameter domain can be obtained and two typical examples in V-\(K_\alpha\) and V-\(K_y\) plane domain have been displayed in Fig. 9a, b, respectively.

In Fig. 9a, there exist two boundaries \(l_1\) and \(l_2\), through which the equilibrium O loses its stability and some kind of bifurcation will take place. In order to identify the bifurcation type of boundaries, it is required to compute the eigenvalues of \(A_1\). when the following condition is satisfied

$$\begin{aligned}&-5.4588\cdot 10^{28}V^8-1.0913\cdot 10^{38}V^7 +\left( 2.8101\cdot 10^{39}K_\alpha +2.7189\cdot 10^{40}\right) V^6\nonumber \\&\quad +\left( 1.1002\cdot 10^{41}K_\alpha +8.1027\cdot 10^{41}\right) V^5 +\left( 3.3208\cdot 10^{42} K_\alpha -2.1527\cdot 10^{40}K_\alpha ^2\right. \nonumber \\&\quad \left. -2.5162\cdot 10^{43}\right) V^4 +\left( 7.0014\cdot 10^{43}K_\alpha -8.8529\cdot 10^{41} K_\alpha ^2-1.2827\cdot 10^{45}\right) V^3\nonumber \\&\quad -\left( 1.3653\cdot 10^{43}K_\alpha ^2-7.7698 \cdot 10^{44}K_\alpha +1.7603\cdot 10^{46}\right) V^2 -\left( 9.0141\cdot 10^{46}\right. \nonumber \\&\quad \left. +9.3582\cdot 10^{43}K_\alpha ^2 -4.0008\cdot 10^{45}K_\alpha \right) V + 7.3068\cdot 10^{45}K_\alpha \nonumber \\&\quad -2.4054\cdot 10^{44}K_\alpha ^2-1.1927\cdot 10^{47}=0, \end{aligned}$$
(8)

there exists a pair of purely imaginary eigenvalues \(\pm \omega i\) in A.

Coincidentally, the Eq. (8) corresponds exactly to the curve \(l_1\). When the parameters cross the boundary \(l_1\), a family of stable limit cycles will bifurcate and a typical bifurcation diagram for \(V=26\)m/s is demonstrated in Fig. 10 with \(K_\alpha\) as a bifurcation parameter, which shows that at H\(_1\) the equilibrium O loses stability through a Hopf bifurcation and \(l_1\) is a supercritical Hopf bifurcation curve.

If the following condition is met

$$\begin{aligned} K_\alpha -0.003765V^2=0, \end{aligned}$$
(9)

there exists a zero eigenvalue in the matrix \(A_1\), which is just to be the algebraic expression of the curve \(l_2\). When the parameter \(K_\alpha\) crosses the curve \(l_2\) from up to down, the equilibrium O loses its stability by undergoing a branch point bifurcation. Figure 10 shows that two symmetrical stable equilibrium branches bifurcate from the point BP\(_1\), which indicates that \(l_2\) is a supercritical pitchfork bifurcation curve.

Fig. 9
figure 9

a Stable domain in V–\(K_\alpha\) plane for the equilibrium O with \(K_y=2863\) N/m. b Stable domain in V–\(K_y\) plane for the equilibrium O with \(K_\alpha =2.57\) N m/rad

Full size image
Fig. 10
figure 10

A one-parameter bifurcation diagram for \(V=26\) m/s and \(K_\alpha\) as a bifurcation parameter

Full size image

In Fig. 9b, there also exist two boundaries \(l_3\) and \(l_4\). By analysis, it has been found that the curves \(l_3\) and \(l_4\) are corresponding to a zero eigenvalue and a pair of purely imaginary eigenvalues of the matrix \(A_1\), respectively, whose expressions are deduced as following

$$\begin{aligned} \left\{ \begin{array}{l} l_3:\ V=26.125,\\ l_4:\ -7.0439\cdot 10^{18}V^5+(6.8315\cdot 10^{17}K_y +4.1018\cdot 10^{20})V^4 +(4.8337\cdot 10^{18}K_y\\ \quad +8.7269\cdot 10^{21})V^3 -(2.5716\cdot 10^{17}K_y^2-9.9352\cdot 10^{19}K_y -2.5433\cdot 10^{22})V^2\\ \quad -(4.96\cdot 10^{18}K_y^2-1.3929\cdot 10^{21}K_y +2.4848\cdot 10^{23})V -8.8459\cdot 10^{18}K_y^2\\ \quad +3.9866\cdot 10^{21}K_y-1.0427\cdot 10^{24}=0. \end{array}\right. \end{aligned}$$
Fig. 11
figure 11

a Bifurcation diagram for \(K_y=1650\) N/m. b Bifurcation diagram for \(K_y=2400\) N/m

Full size image

Combined with Fig. 9b, a typical bifurcation diagram for \(K_y\) = 1650 N/m and V as a continuation parameter is displayed in Fig. 11a. It has been shown that, with the increase of V from left to right, the point H\(_2\) on \(l_4\) is encountered, which shows that the equilibrium O loses its stability through a Hopf bifurcation and a series of stable limit cycles bifurcates from the point H\(_2\).

As the velocity V moves right further, the point BP\(_2\) on \(l_3\) has been encountered, through which the unstable equilibrium O undergoes a pitchfork bifurcation and then two additionally unstable equilibrium branches arise, which shows that BP\(_2\) is a subcritical pitchfork bifurcation point. On the green equilibrium branches, two Hopf points H\(_3\) and H\(_4\) have been met, across which the upper branch and the down branch obtain their stability, respectively. Wherein H\(_3\) is a supercritical Hopf point, from which a series of stable limit cycles bifurcates to the left and coincides with the limit cycles from the point H\(_2\). While the point H\(_4\) is a subcritical Hopf point, from which a series of unstable limit cycles bifurcates to the right.

Two stable limit cycles for \((K_y,V)=(1650,24)\) and \((K_y,V)=(1650,26.2)\) have been separately displayed in Fig. 12a, b, which emanate from the points H\(_2\) and H\(_3\), respectively. When V is on the right of H\(_4\), the system presents bistable states with two equilibria, which is exhibited in Fig. 13 for \((K_y,V)=(1650,27)\).

Fig. 12
figure 12

a A stable limit cycle for \((K_y,V)=(1650,24)\), which bifurcates from the point H\(_2\) in Fig. 11a. b For \((K_y,V)=(1650,26.2)\), a stable limit cycle bifurcating from the point H\(_3\) in Fig. 11a

Full size image
Fig. 13
figure 13

Bistable states for \((K_y,V)=(1650,27)\)

Full size image

From Fig. 9b, a bifurcation structure for \(K_y=2400\) N/m has been presented in Fig. 11b, which shows that, with the increase of V, a branch point BP\(_3\) will be encountered first and then a Hopf point H\(_5\) will come across. From BP\(_3\) there are two symmetrically stable equilibrium branches emanating and from H\(_5\) a series of unstable limit cycles is bifurcated.

Figure 11a together with Fig. 11b shows that the curve \(l_3\) in Fig. 9b is divided into the upper supercritical branch and the lower subcritical one, and simultaneously \(l_4\) is divided into the left supercritical branch and the right subcritical one, respectively. The intersection point of \(l_3\) and \(l_4\) is a zero-Hopf bifurcation point.

Remarks

  • From Fig. 9a, b, it is observed that the origin O is stable in the shadow area and unstable in the black area. That \(l_1\) and \(l_2\) (\(l_3\) and \(l_4\)) intersect at a point indicates that they are divided into supercritical branches and subcritical branches. When the parameters cross the line \(l_2\) or \(l_3\) from shaded areas to black areas, two stable nontrivial equilibria will be generated. However, When the parameters cross the line \(l_2\) or \(l_3\) from black areas to black areas, two unstable nontrivial equilibria will be produced. The same goes for the lines \(l_1\) or \(l_4\), through which stable or unstable limit cycles will emerge.

  • The analysis of stable domain of the equilibrium O in \(K_y\)-\(K_\alpha\) plane is omitted due to its same bifurcation type of the boundaries.

  • The cubic and the quintic nonlinearity in stiffness do not affect the stability of the origin O. Hence, there is no need to discuss this section. Bifurcation structure of the equilibrium O as for the other parameters is not distinct or same. So the other cases have not been analyzed here.

  • Generally speaking, if a wing model undergoes a Hopf bifurcation, nonlinear effects can lead to supercritical or subcritical postflutter responses. When the postflutter response is supercritical, limit-cycle oscillations(LCOs) smoothly arise after flutter has occurred. This situation is not concerning for design because the wing does not operate beyond the flutter boundary by certification [5]. However, when the postflutter response is subcritical, a bistability region will exist where two attractors, one equilibrium and a large LCO, will coexist and the unstable limit-cycle acts as the separatrix of the bistability region. A large perturbation could suddenly push the system into the basin of attraction of the large LCO even before flutter occurs. So the subcritical Hopf bifurcation is adverse and undesirable.

5 Bifurcation Structure of Equilibria and Limit Cycles in V–\(K_y\) Plane

As an extension of Fig. 9b, bifurcation structure of equilibria, including trivial and nontrivial ones, as well as limit cycles has been discussed here as shown in Fig. 14, where the domain near the point ZH has been divided into six parts.

Fig. 14
figure 14

The curves \(l_3\) and \(l_4\) are the same meaning as those in Fig. 9b. The green curve \(l_5\) is a Hopf bifurcation curve of the nontrivial equilibria

Full size image

When the parameter pairs \((V,K_y)\) are chosen in region \(\textcircled {1}\), there exists a stable trivial equilibrium O. A typical phase diagram for \((V,K_y)=(26,2200)\) from the initial values \((-0.13,-0.21,-0.11,-0.12)\) has been displayed in Fig. 15a, which indicates that under small perturbations the plunge variable \(y_1\) and the pitch angle \(y_3\) will both tend to the stable state O.

When the parameter pairs \((V,K_y)\) are chosen in region \(\textcircled {2}\), a stable limit cycle exists. A typical phase diagram for \((V,K_y)=(26,1800)\) from the initial values (\(-\)0.04, \(-\)0.06, 0.03, 0.09) has been displayed in Fig. 15b, which indicates that a small perturbation will make the wing present periodic vibration in plunge and pitch direction.

As the parameters cross the line \(l_3\) from region \(\textcircled {2}\) into region \(\textcircled {3}\), the unstable equilibrium O undergoes a subcritical pitchfork bifurcation and two extra unstable nontrivial equilibria emerge.

When the parameters cross the left branch of line \(l_5\) into region \(\textcircled {4}\), one of two nontrivial equilibria obtains its stability. A phase diagram for \((V,K_y)=(26.315,1650)\) has been displayed in Fig. 15c, where a trajectory from a point near p\(_2\) tends to p\(_1\), which indicates that the upper equilibrium p\(_1\) is stable while the lower one p\(_2\) is unstable. This shows that there exists an equilibrium state with an upward pitch angle and an upward plunge displacement.

When the parameters cross the right branch of line \(l_5\) into region \(\textcircled {5}\), the other nontrivial equilibrium obtains its stability and now there are two stable equilibria p\(_3\) and p\(_4\). In addition, it is indicated that the initial position of pitch angle \(y_3\) or \(\alpha\) will play a leading role and determine which equilibrium to be tended.

When the parameters enter into region \(\textcircled {6}\), there also exist two stable equilibria. The difference between region \(\textcircled {5}\) and region \(\textcircled {6}\) is that through the line \(l_4\) from up to down, the unstable equilibrium O experiences a subcritical Hopf bifurcation and a series of unstable limit cycles bifurcate from the line \(l_4\), which has not been presented here.

Fig. 15
figure 15

a The stable equilibrium O. b A stable limit cycle. c \(P_1\) and \(P_2\) are a stable and an unstable equilibrium, respectively. d Two stable nontrivial equilibria \(P_3\) and \(P_4\) coexist

Full size image

6 Conclusions

A wing model with high nonlinearity has been discussed in this paper. Based on different continuation parameters V, \(\xi _2\) and \(\zeta _2\), the bifurcation behavior of trivial and nontrivial equilibria has been investigated here. It is shown that \(\xi _2\) has little effect on the stability performance of all the equilibria; however \(\zeta _2\) has affected the number and stability of nontrivial equilibria; nevertheless the velocity V has influenced the bifurcation structure of all the equilibria, including the trivial and the nontrivial. Figure 11a shows that although these two symmetrical nontrivial equilibria are produced simultaneously by a pitchfork bifurcation and with the same stability at first, they severally undergo two types of Hopf bifurcation at different parameter values. The upper equilibrium branch experiences a supercritical Hopf bifurcation, accompanied with a series of stable limit cycles, which coincides with the limit cycles bifurcated from the Hopf point of the equilibrium O. While the lower equilibrium branch undergoes a subcritical Hopf bifurcation, where a family of unstable limit cycles appear. That two types of Hopf bifurcation happen at different points indicates that two nontrivial equilibria are not always with the same stability and there exists a parameter region where only one nontrivial equilibrium is stable.