Eigenvalues and Eigenfunctions of One-Dimensional Fractal Laplacians

Abstract

We study the eigenvalues and eigenfunctions of one-dimensional weighted fractal Laplacians. These Laplacians are defined by self-similar measures with overlaps. We first prove the existence of eigenvalues and eigenfunctions. We then set up a framework for one-dimensional measures to discretize the equation defining the eigenvalues and eigenfunctions, and obtain numerical approximations of the eigenvalue and eigenfunction by using the finite element method. Finally, we show that the numerical eigenvalues and eigenfunctions converge to the actual ones and obtain the rate of convergence.

1 Introduction

Let $\mu$ be a continuous, positive, finite Borel measure on ${\mathbb R}$ with support $\textrm{supp}(\mu )= [a, b]$. Consider the non-negative quadratic form ${{\mathcal {E}}}(\cdot ,\cdot )$ in $L^2((a, b), \mu )$ defined by

$$\begin{aligned} {{\mathcal {E}}}(u, v):=\int ^b_a u'(x)v'(x) dx, \end{aligned}$$

with domain $\textrm{dom}\,{{\mathcal {E}}}$ equal to the Sobolev space

$$\begin{aligned} H^1_0 (a, b):= \{u\in L^2((a, b), dx): u'\in L^2((a, b), dx), u(a) = u(b) = 0\} \end{aligned}$$

(Dirichlet boundary condition). It is well known that $\textrm{dom}\,{{\mathcal {E}}}$ is dense in $L^2((a, b), \mu )$, and the quadratic form $({{\mathcal {E}}},\textrm{dom}\,{{\mathcal {E}}})$ is closed. Hence there exists a non-negative self-adjoint operator $A_D$ such that

$$\begin{aligned} \textrm{dom}\,{{\mathcal {E}}}=\textrm{dom}\,(A_D^{1/2}) \quad \text{ and }\quad {{\mathcal {E}}}(u,v)=(A_D^{1/2} u,A_D^{1/2}v)_\mu \end{aligned}$$

for all $u,v\in \textrm{dom}\,{{\mathcal {E}}}$. We write $-\Delta _\mu ^D:=A_D$ and call it the (Dirichlet) Laplacian with respect to $\mu$. If no confusion is possible, we denote $\Delta _\mu ^D$ simply by $\Delta _\mu$. Throughout this paper, we let

$$\begin{aligned} \Vert \cdot \Vert _{\textrm{dom}\,{{\mathcal {E}}}}=\sqrt{{{\mathcal {E}}}(\cdot ,\cdot )}. \end{aligned}$$

Recently, the Dirichlet Laplacian $\Delta _{\mu }$ has been studied extensively in connection with fractal measures (see [1,2,3,4, 6,7,8,9,10,11,12, 14,15,17, 19, 20, 22, 25,26,28] and the references therein). These papers mainly study the spectral asymptotics of $\Delta _\mu$ and the associated Schrödinger operators, and wave, heat, and Schrödinger equations defined by $\Delta _\mu$.

In this paper, we consider the following eigenvalue problem

$$\begin{aligned} -\Delta _\mu u=\lambda V(x)u\qquad x\in (a,b), \end{aligned}$$

(1.1)

where $V:[a,b]\rightarrow [0,+\infty )$. We say $\lambda$ is an eigenvalue of Eq. (1.1) corresponding to a non-zero eigenfunction $\varphi (x)\in \textrm{dom}\,{{\mathcal {E}}}$ if

$$\begin{aligned} {{\mathcal {E}}}(\varphi ,v)=\lambda (V\varphi ,v)_\mu \end{aligned}$$

holds for all $v\in \textrm{dom}\,{{\mathcal {E}}}$. We remark that for the case $V\equiv 1$, the finite element method is used to obtain numerical solutions to the eigenproblem (1.1) for self-similar measures satisfying a family of second-order self-similar identities in [3]. These identities were first introduced by Strichartz and are used in [24] to approximate the density of the infinite Bernoulli convolution associated with the golden ratio. To the best of the authors’ knowledge, in the absence of second-order identities, the eigenvalue problem defined by IFSs with overlaps has not been obtained before, and this is a main motivation of this paper.

The first objective of this paper is to obtain the existence result of eigenvalues and eigenfunctions of (1.1).

Theorem 1.1

Let $V(x)\ge 0$ on [a, b] with $c_V:= \Vert V\Vert _{L^1((a,b),\mu )}>0$. Then there exists a complete orthonormal basis $\{\varphi _n\}_{n=1}^\infty$ of $L^2((a,b), \mu )$ such that each $\varphi _n$ is an eigenfunction of Eq. (1.1) corresponding to an eigenvalue $\lambda _n$ satisfying

$$\begin{aligned} 0<\lambda _1\le \lambda _2\le \cdots \le \lambda _n\le \cdots \end{aligned}$$

and $\lim _{n\rightarrow \infty }\lambda _n=\infty$. Moreover, $\{\varphi _n(x)\}_{n=1}^\infty$ also forms an orthogonal basis of $\textrm{dom}\,{{\mathcal {E}}}$.

To prove Theorem 1.1, we modify the classical argument (see [21]) and replace Lebesgue measure by a more general measure $\mu$.

The second objective of this paper is to study Eq. (1.1) from a numerical point of view. Two closed sub-intervals I, J of [a, b] are measure disjoint with respect to $\mu$ if $\mu (I\cap J)=0$. Let $I\subseteq [a,b]$ be a closed interval. We call a finite family ${\textbf{P}}$ of measure disjoint cells a $\mu$-partition of I if $J\subseteq I$ for all $J\in {\textbf{P}}$, and $\mu (I)=\sum _{J\in {\textbf{P}}}\mu (J)$. A sequence of $\mu$-partitions $(\textbf{P}_m)_{m\ge 1}$ of [a, b] is compatible if (1) for any $m\ge 1$, each member of $\textbf{P}_{m+1}$ is a proper subset of some member of $\textbf{P}_m$; (2) for any $m\ge 2$ and any $J\in \textbf{P}_m$, there exist similitudes $(\tau _{IJ})_{I\in \textbf{P}_1}$ of the form $\tau _{IJ} (x)=r_{IJ}x+b_{IJ}$ ($r_{IJ}\in (0,1), b_{IJ}\in {\mathbb R}$) and positive constants $(c_{IJ})_{I\in \textbf{P}_1}$ such that $\tau _{IJ}(I)\subseteq J$ and

$$\begin{aligned} \mu |_{J}=\sum _{I\in \textbf{P}_1} c_{IJ} \cdot \mu |_{I}\circ \tau _{IJ} ^{-1}. \end{aligned}$$

(1.2)

Intuitively, (1.2) means that the $\mu$ measure of each closed interval in $\textbf{P}_m$ for $m\ge 2$ can be expressed as a linear combination of $\{\mu (I):I \in \textbf{P}_1\}$. By making use of (1.2), some results concerning $\Delta _\mu$ have been obtained (see, e.g., [17, 25,26,27]).

In order to discretize (1.1) and obtain numerical approximations of the eigenvalue and eigenfunction, we will assume that there exists a sequence of compatible $\mu$-partitions $(\textbf{P}_m)_{m\ge 1}$. Thus the $\mu$ measure of each closed interval in the partition can be computed by using (1.2), making it possible to discretize the Eq. (1.1). We remark that the assumption $\textrm{supp}(\mu )=[a,b]$ guarantees that the mass matrix that arises in the finite element method is positive definite (see [2, Proposition 3.1]),

Let $V\equiv 1$ in (1.1). If $\lambda$ is an eigenvalue of Eq. (1.1) corresponding to a non-zero eigenfunction $u\in \textrm{dom}\,{{\mathcal {E}}}$, then

$$\begin{aligned} \int _a^b u' v'\,dx =\lambda \int _a^b uv d\mu \qquad \text{ for } \text{ all } v\in \textrm{dom}\,{{\mathcal {E}}}. \end{aligned}$$

(1.3)

Theorem 1.2

Let $\mu$ be a continuous positive finite Borel measure on ${\mathbb R}$ with $\textrm{supp}(\mu )=[a,b]$. Assume that there exists a sequence of compatible $\mu$-partitions $(\textbf{P}_m)_{m\ge 1}$ of [a, b] and the integrals $\int _{I}x^k\, d\mu$, $I\in \textbf{P}_1$, $k=0,1,2$, can be evaluated explicitly. Then Eq. (1.3) can be discretized into a matrix Eq. (3.5) by finite element method. Moreover, Eq. (3.5) can be solved numerically.

We are mainly interested in fractal measures with overlaps. Theorem 1.2 provides a framework under which discretization can be performed. We remark that if self-similar measures $\mu$ satisfies a family of second-order self-similar identities, then $\mu$ satisfies (1.2) (see [26, Proposition 5.1]). Hence, Theorem 1.1 cannot be deduced from [3, Theorem 1.2].

The following theorem shows that the approximate eigenvalues and eigenfunctions obtained in Theorem 1.2 converge to the actual ones, and we also obtain a rate of convergence.

Theorem 1.3

Assume the hypotheses of Theorem 1.2. If there exist constants $r\in (0,1)$ and $c>0$ such that $\max \{|J|:J\in {\textbf{P}}_k\}\le c\, r^{k}$ for all $k\ge 1$, then the numerical eigenvalues $\hat{\lambda }_n^{(m)}$ and normalized eigenfunctions $\hat{\varphi }_n^{(m)}$, obtained in Theorem 1.2, converge to the corresponding theoretical $\lambda _n$ and $\varphi _n$, respectively. Moreover, for each $n\ge 1$, there exists a constant $C:=C(n)>0$ (depending only on n) such that for all $m\ge 1$,

$$\begin{aligned} \lambda _n\le \hat{\lambda }_n^{(m)}\le \lambda _n+Cr^{m/2} \lambda _n \quad \text{ and }\quad \Vert \varphi _n-\hat{\varphi }_n^{(m)}\Vert \le C r^{m/2}. \end{aligned}$$

(4)

We illustrate Theorems 1.2 and 1.3 by a class of self-similar measures with overlaps that we call essentially of finite type (EFT) (see [19]). This class is used in [19] to illustrate self-similar measures satisfying EFT. These measures have been studied extensively (see, e.g., [16, 25, 27]). However, it is not clear whether they satisfy a family of second-order identities.

The rest of this paper is organized as follows. In Sect. 2, we prove Theorem 1.1. In Sect. 3, we give the proofs of Theorems 1.2 and 1.3, and apply them to a class of self-similar measures with overlaps.

2 Existence of Eigenvalues and Eigenfunctions

In this section, we mainly prove Theorem  1.1. The technique used here is the same in spirit as in classical setting.

Proof of Theorem 1.1

Step 1. We show the existence of the smallest eigenvalue $\lambda _1$. We remark that for each $u\in \textrm{dom}\,{{\mathcal {E}}}$,

$$\begin{aligned} |u(x)|=\Big |\int _a^xu'(x)\,dx\Big |\le (b-a)^{1/2} {{\mathcal {E}}}^{1/2}(u,u) \end{aligned}$$

for all $x\in [a,b]$. Then $\sup _{x\in [a,b]}|u(x)| \le (b-a)^{1/2} {{\mathcal {E}}}^{1/2}(u,u)$ for all $u\in \textrm{dom}\,{{\mathcal {E}}}$. It follows that

$$\begin{aligned} (Vu,u)_\mu = \int _a^b V(x)u^2(x)\,d\mu (x)\le (b-a){{\mathcal {E}}}(u,u)\int _a^b V(x)\,d\mu =\beta {{\mathcal {E}}}(u,u) \end{aligned}$$

(1.4)

for all $u\in \textrm{dom}\,{{\mathcal {E}}}$, where $\beta :=(b-a)c_V$. Define the Rayleigh quotient R(u) on $\textrm{dom}\,{{\mathcal {E}}}$ by

$$\begin{aligned} R(u):= \frac{{{\mathcal {E}}}(u,u)}{( Vu,u)_\mu }, \quad u\ne 0. \end{aligned}$$

Together with (2.1), it yields

$$\begin{aligned} R(u)\ge \frac{{{\mathcal {E}}}(u,u)}{\beta {{\mathcal {E}}}(u,u)}=\frac{1}{\beta } \quad \text{ for } \text{ all } u\in \textrm{dom}\,{{\mathcal {E}}}\text{, } u\ne 0\text{. } \end{aligned}$$

Hence, R(u) has a positive infimum. Let $\mathcal {A}=\{u\in \textrm{dom}\,{{\mathcal {E}}}: (Vu,u)_ \mu =1\}$. We define

$$\begin{aligned} \lambda _1:=\inf _{u\in \textrm{dom}\,{{\mathcal {E}}},\;u\ne 0}R(u)=\inf _{u\in \mathcal {A}}{{\mathcal {E}}}(u,u). \end{aligned}$$

(2.1)

Then $\lambda _1\ge 1/\beta >0$. We claim that $\lambda _1$ is the smallest eigenvalue of Eq. (1.1). We choose a minimising sequence $\{u_m\}\subset \mathcal {A}$ such that

$$\begin{aligned} R(u_m)={{\mathcal {E}}}(u_m,u_m)\rightarrow \lambda _1. \end{aligned}$$

(2.2)

By the definition of $\mathcal {A}$, we have the sequence $\{u_m\}$ is bounded in $\textrm{dom}\,{{\mathcal {E}}}$. Combining it with the fact $\textrm{dom}\,{{\mathcal {E}}}$ is compactly embedded into the space $C_0(a,b):=\{u\in C(a,b):u(a)=u(b)=0\}$, there exists a subsequence (also denoted by $\{u_m\}$, for convenience) and a function $\varphi _1\in C_0(a,b)$ such that

$$\begin{aligned} \lim _{m\rightarrow \infty } \sup _{x\in [a,b]}|u_m(x)-\varphi _1(x)|=0. \end{aligned}$$

Thus we can deduce from the Lebesgue dominated convergence theorem that

$$\begin{aligned} (V\varphi _1,\varphi _1)_\mu =1. \end{aligned}$$

(2.3)

Combining Eqs. (2.2)–(2.4) and the fact that

$$\begin{aligned} {{\mathcal {E}}}(u_m-u_k,u_m-u_k)+{{\mathcal {E}}}(u_m+u_k,u_m+u_k)=2\big ({{\mathcal {E}}}(u_m,u_m)+{{\mathcal {E}}}(u_k,u_k)\big ), \end{aligned}$$

we can see that

$$\begin{aligned} \begin{aligned} {{\mathcal {E}}}(u_m-u_k,u_m-u_k)&\le 2\big ({{\mathcal {E}}}(u_m,u_m)+{{\mathcal {E}}}(u_k,u_k)\big ) -\lambda _1 \big (V(u_m+u_k), u_m+u_k\big )_ \mu \\&\rightarrow 4\lambda _1-4\lambda _1 (V\varphi _1,\varphi _1)_\mu =0 \qquad \text{ as } m,k\rightarrow \infty , \end{aligned} \end{aligned}$$

which implies that $\{u_m\}$ is a Cauchy sequence in $\textrm{dom}\,{{\mathcal {E}}}$. Hence

$$\begin{aligned} u_m\rightarrow \varphi _1\qquad \text{ in } \textrm{dom}\,{{\mathcal {E}}} \quad \text{ and }\quad \lambda _1={{\mathcal {E}}}(\varphi _1,\varphi _1). \end{aligned}$$

(2.4)

For $w\in \textrm{dom}\,{{\mathcal {E}}}$, we define $g(t):=R(\varphi _1+tw)$. Then

$$\begin{aligned} \begin{aligned} g(t)=\frac{{{\mathcal {E}}}(\varphi _1,\varphi _1)+2t{{\mathcal {E}}}(\varphi _1,w)+t^2{{\mathcal {E}}}(w,w)}{(V\varphi _1,\varphi _1)_\mu +2t (V\varphi _1,w)_\mu +t^2(Vw,w)_\mu }. \end{aligned} \end{aligned}$$

It follows from (2.2) and (2.5) that g(t) reaches its minimum at $t=0$. Then $g'(0)=0$. By virtue of (2.4) and (2.5), we have

$$\begin{aligned} \begin{aligned} g'(0)&=\frac{2{{\mathcal {E}}}(\varphi _1,w)(V\varphi _1,\varphi _1)_\mu -2{{\mathcal {E}}}(\varphi _1,\varphi _1)(V\varphi _1,w)_\mu }{(V\varphi _1,\varphi _1)_\mu ^2}\\&=\frac{2\Big ({{\mathcal {E}}}(\varphi _1,w)-\lambda _1(V\varphi _1,w)_\mu \Big )}{(V\varphi _1,\varphi _1)_\mu }=0 \end{aligned} \end{aligned}$$

for all $w\in \textrm{dom}\,{{\mathcal {E}}}$, which implies that $\lambda _1$ is an eigenvalue of Eq. (1.1). We remark that $\lambda _1$ is the smallest eigenvalue following from (2.2).

Step 2. We prove the existence of the smallest eigenvalues $\lambda _2\le \lambda _3\le \cdots$. Since the existence of $\lambda _1$ has been obtained, we can assume that there exists $m-1$ eigenvalues $\lambda _1\le \lambda _2\le \cdots \le \lambda _{m-1}$ with corresponding to the eigenfunctions $\varphi _1,\varphi _2,\cdots ,\varphi _{m-1},$ and $(V\varphi _k,\varphi _k)_\mu =1$ for all $k=1,2,\cdots ,m-1$, where $m\ge 2$. We define

$$\begin{aligned} \begin{aligned} E_{m-1}&:=\textrm{span}\{\varphi _1,\cdots ,\varphi _{m-1}\},\\ E^{\bot }_{m-1}&:=\{\varphi :\varphi \ne 0 \text{ and } (V\varphi ,w)_\mu =0 \text{ for } \text{ all } w\in E_{m-1}\}. \end{aligned} \end{aligned}$$

Similarly, we can prove that there exist some positive constant $\lambda _m$ and $\varphi _m\in \textrm{dom}\,{{\mathcal {E}}}\cap E^{\perp }_{m-1}$ satisfying $(V\varphi _m,\varphi _m)_\mu =1$, and ${{\mathcal {E}}}(\varphi _m,w)=\lambda _m(V\varphi _m,w)_\mu$ for all $w\in \textrm{dom}\,{{\mathcal {E}}}\cap E^\perp _{m-1}$. Furthermore,

$$\begin{aligned} \lambda _m=R(\varphi _m)=\inf _{u\in \textrm{dom}\,{{\mathcal {E}}}\cap E^{\perp }_{m-1},u\ne 0 } R(u). \end{aligned}$$

For each $w\in \textrm{dom}\,{{\mathcal {E}}}$, we can write w as

$$\begin{aligned} w=w_1+w_2, \quad w_1=\sum _{k=1}^{m-1}\alpha _k \varphi _k\in E_{m-1}, \quad w_2\in E^{\perp }_{m-1}. \end{aligned}$$

It follows that

$$\begin{aligned} \begin{aligned} {{\mathcal {E}}}(\varphi _m,w)&={{\mathcal {E}}}(\varphi _m,w_1)+{{\mathcal {E}}}(\varphi _m,w_2) =\sum _{k=1}^{m-1}\alpha _k{{\mathcal {E}}}(\varphi _m,\varphi _k)+{{\mathcal {E}}}(\varphi _m,w_2)\\&={{\mathcal {E}}}(\varphi _m,w_2)=\lambda _m(V\varphi _m,w_2)_\mu =\lambda _m(V\varphi _m,w_1+w_2)_\mu =\lambda _m(V\varphi _m,w)_\mu \end{aligned} \end{aligned}$$

for all $w\in \textrm{dom}\,{{\mathcal {E}}}$. Thus $\lambda _m$ is an eigenvalue of Eq. (1.1). It is easy to see that $\lambda _m\ge \lambda _{m-1}$. Therefore, Eq. (1.1) has a sequence of positive eigenvalues such that $0<\lambda _1\le \lambda _2\le \cdots \le \lambda _m\le \cdots$.

Step 3. We show that for any distinct eigenvalues $\lambda _i$ and $\lambda _j$, the corresponding eigenfunctions $\varphi _i$ and $\varphi _j$ are orthogonal in $\textrm{dom}\,{{\mathcal {E}}}$, that is

$$\begin{aligned} {{\mathcal {E}}}(\varphi _i,\varphi _j)=0. \end{aligned}$$

(2.5)

Since $0={{\mathcal {E}}}(\varphi _i,\varphi _j)-{{\mathcal {E}}}(\varphi _j,\varphi _i)=\lambda _i(V\varphi _i,\varphi _j)_\mu -\lambda _j(V\varphi _j,\varphi _i)_\mu$, we have

$$\begin{aligned} (\lambda _i-\lambda _j)(V\varphi _i,\varphi _j)_\mu =0, \end{aligned}$$

which implies (2.6).

Step 4. We claim that the dimension of the space consisting of eigenfunctions corresponding to a fixed eigenvalue is finite. Suppose, on the contrary, that there exists countably infinite sequence of eigenfunctions $\{\phi _k\}_{k=1}^\infty$ corresponding to the same eigenvalue $\lambda$, which are linearly independent in $\textrm{dom}\,{{\mathcal {E}}}$. So we can renormalize such that

$$\begin{aligned} (V\phi _k,\phi _k)_\mu =1\qquad \text{ for } \text{ all } k\ge 1. \end{aligned}$$

Since ${{\mathcal {E}}}(\phi _k,\phi _k)=\lambda (V\phi _k,\phi _k)_\mu =\lambda$, there exists a convergent subsequence of $\{\phi _k\}$ in $C_0(a,b)$. However, we can see that

$$\begin{aligned} \begin{aligned} (V(\phi _l-\phi _k),\phi _l-\phi _k)_\mu&=(V\phi _l,\phi _l)_\mu +(V\phi _k,\phi _k)_\mu -2(V\phi _l,\phi _k)_\mu \\&=(V\phi _l,\phi _l)_\mu +(V\phi _k,\phi _k)_\mu =2, \quad \text{ if } l\ne k\text{, } \end{aligned} \end{aligned}$$

which is a contradiction. Thus the claim holds.

Step 4. We show that

$$\begin{aligned} \lim _{n\rightarrow \infty } \lambda _n=+\infty . \end{aligned}$$

(2.6)

Suppose, on the contrary, that there exists some positive constant M such that $0<\lambda _n\le M$ for all $n\ge 1$. Without loss of generality, we assume that the sequence of corresponding eigenfunctions $\{\varphi _n\}$ is orthogonal in $L^2((a,b),Vd\mu )$. Then

$$\begin{aligned} {{\mathcal {E}}}(\varphi _n,\varphi _n)=\lambda _n(V\varphi _n,\varphi _n)_\mu \le M, \end{aligned}$$

and hence there exists a convergent subsequence of $\{\varphi _m\}$ in the space $C_0(a,b)$, which is a contradiction, since $(V(\varphi _m-\varphi _k),\varphi _m-\varphi _k)_\mu =2$. Thus (2.7) holds.

Step 5. We show that the eigenfunctions $\{\varphi _m\}$ corresponding to $\{\lambda _m\}$ form a basis of $\textrm{dom}\,{{\mathcal {E}}}$. Suppose that there exists some non-zero $w\in \textrm{dom}\,{{\mathcal {E}}}$ such that ${{\mathcal {E}}}(\varphi _m,w)=0$ for all $m\ge 1$. Then $(V\varphi _m,w)_\mu ={{\mathcal {E}}}(\varphi _m,w)/\lambda _m=0$ for all $m\ge 1$. Therefore, $w\in E^\perp _{m-1}$ for all $m\ge 2$, which implies

$$\begin{aligned} \lambda _m\le R(w)=\frac{{{\mathcal {E}}}(w,w)}{(Vw,w)_\mu }, \qquad m\ge 2. \end{aligned}$$

(2.7)

However, $\lambda _m\rightarrow \infty$ as $m\rightarrow \infty$, and then (2.8) is impossible. Hence, the desired result holds. $\square$

Since $\textrm{dom}\,{{\mathcal {E}}}$ is dense in $C_0(a,b)$, we see that $\{\varphi _m\}_{m=1}^\infty$ is also an orthogonal basis of $L^2((a,b),Vd\mu )$. We remark that $(V\varphi _m,\varphi _m)_\mu =1$. Thus $\{\varphi _m\}_{m=1}^\infty$is an orthonormal basis of $L^2((a,b),Vd\mu )$. It is well known that $\mu$ can also define a Neumann Laplace operator $\Delta _\mu ^N$ in $L^2((a,b),\mu )$. We remark that the eigenproblem (1.1) replacing $\Delta _\mu$ by $\Delta _\mu ^N$ also has a sequence of orthogonal eigenfunctions in $L^2((a,b),\mu )$, but the first eigenvalue is zero, corresponding to the constant eigenfunction. The proof is similar to that of Theorem 1.1. We omit the details.

Corollary 2.1

Assume the hypotheses of Theorem 1.1 and let $\lambda _1$ be the first eigenvalue of eigenproblem (1.1). Then there exists a non-negative eigenfunction corresponding to $\lambda _1$.

Proof

Let $\varphi _1$ be an eigenfunction of (1.1) corresponding to $\lambda _1$. It suffices to prove that $|\varphi _1|$ is also an eigenfunction corresponding to $\lambda _1$. We remark that $|\varphi _1|\in \textrm{dom}\,{{\mathcal {E}}}$ and ${{\mathcal {E}}}(|\varphi _1|,|\varphi _1|)\le {{\mathcal {E}}}(\varphi _1,\varphi _1)$. Combining it with (2.4) and (2.5), we can see that

$$\begin{aligned} R(|\varphi _1|)\le \lambda _1. \end{aligned}$$

(2.8)

On the other hand, by the definition of $\lambda _1$, we have

$$\begin{aligned} R(|\varphi _1|)\ge \lambda _1. \end{aligned}$$

(2.9)

Thus the desired result follows by combining (2.9) and (2.10). $\square$

3 The Finite Element Method and Convergence of Numerical Solutions

In this section, we mainly prove Theorems 1.2 and 1.3. Let $V \equiv 1$ in Eq. (1.1). We first use the finite element method to solve the equation, and then prove the convergence of numerical approximations of the eigenvalue and eigenfunction.

Let $\mu$ be a continuous positive finite Borel measure on ${\mathbb R}$ with $\textrm{supp}(\mu )=[a,b]$, and $(\textbf{P}_m)_{m\ge 1}=(\{I_{m,i}\}_{i=1}^{N(m)})_{m\ge 1}$ be a sequence of $\mu$-partitions of [a, b]. Thus we can write $I_{m,i}=[x_{m,i-1},x_{m,i}]$ for $m\ge 1$ and $1\le i \le N(m)$. Note that $x_{m,0}=a$ and $x_{m,N(m)}=b$ for all $m\ge 1$. Let $W_m:=\{x_{m,i}:i=0,\dots ,N(m)\}$ be the set of end-points of all level-m subintervals in $\textbf{P}_m$, and $S^m$ be the space of continuous piecewise linear functions on [a, b] with nodes $W_m$, and let

$$\begin{aligned} S_D^m=\{u\in S^m:u(a)=u(b)=0\} \end{aligned}$$

be the subspaces of $S^m$ consisting of functions satisfying the Dirichlet boundary condition. Then

$$\begin{aligned} \dim (S^m)=N(m)+1\quad \text{ and }\quad \dim (S_D^m)=N(m)-1. \end{aligned}$$

We choose the basis of $S^m$ consisting of the following tent functions:

$$\begin{aligned} \phi _{m,{i}}(x):= {\left\{ \begin{array}{ll} \begin{aligned}&{} \frac{x-x_{m,i-1}}{x_{m,i}-x_{m, i-1}}\quad &{}&{}\text{ if } x\in I_{m,i},\, i=1,2,\dots ,N(m),\\ &{}\frac{x-x_{m, i+1}}{x_{m,i}-x_{m,i+1}}\quad &{}&{}\text{ if } x\in I_{m,i+1},\, i=0,1,\dots ,N(m)-1,\\ &{}0\quad &{}&{}\text {otherwise}, \end{aligned} \end{array}\right. } \end{aligned}$$

(2.10)

and choose the basis $\{\phi _{m,i}\}_{i=1}^{N(m)-1}$ for $S_D^m$.

Proof of Theorem 1.2

Use the notation above. We use the finite element method to discretize Eq. (1.3). Let u(x) be an eigenfunction of Eq. (1.1) corresponding to an eigenvalue $\lambda$, that is, u(x) satisfies Eq. (1.3). We approximate u(x) by

$$\begin{aligned} u_m(x)=\sum _{i=0}^{N(m)}w_{m,i}\phi _{m,i}\qquad \text{ for } m\ge 1\text{, } \end{aligned}$$

(3.1)

where each $w_{m,i}$ is a constant to be determined. Fix any $m\ge 1$. We require $u_m(x)$ to satisfy the integral form of the eigenvalue equation

$$\begin{aligned} \begin{aligned} \int _a^b u'_m \phi '_{m,j}\, d x = \lambda \int _a^bu_m\phi _{m,j}\, d\mu \end{aligned} \end{aligned}$$

(3.2)

for $j=1,\dots ,N(m)-1$, and the Dirichlet boundary condition $u_m(x)=0$ on $\{a,b\}$. It follows that $w_{m,0}=w_{m,N(m)}=0$. Using this and substituting (3.2) into (3.3), we can deduce that

$$\begin{aligned} \begin{aligned} \sum _{i=1}^{N(m)-1}w_{m,i}\int _a^b\phi '_{m,i}(x)\phi '_{m,j}(x)\, d x=\lambda \sum _{i=1}^{N(m)-1}w_{m,i}\int _a^b\phi _{m,i}(x)\phi _{m,j}(x)\, d\mu \end{aligned} \end{aligned}$$

(3.3)

for $1\le j \le N(m)-1$. We define the mass matrix $\textbf{M}=\textbf{M}^{(m)}=(M_{ij}^{(m)})$ and stiffness matrix $\textbf{K}=\textbf{K}^{(m)}=(K_{ij}^{(m)})$, respectively, by

$$\begin{aligned} M_{ij}^{(m)}=\int _a^b\phi _{m,i}(x)\phi _{m,j}(x)\, d\mu \quad \text{ and }\quad K_{ij}^{(m)}=\int _a^b\phi '_{m,i}(x)\phi '_{m,j}(x)\, d x,\quad \end{aligned}$$

where $1\le i,j\le N(m)-1$. Thus $\textbf{M}$ and $\textbf{K}$ are tridiagonal following from the definition of $\phi _{m,j}(x)$. Hence, (3.4) can be expressed into matrix form as

$$\begin{aligned} \textbf{K}{} \textbf{w}=\lambda \textbf{M}{} \textbf{w}, \end{aligned}$$

(3.4)

where

$$\begin{aligned} \textbf{w}=\textbf{w}_m:= \begin{bmatrix} w_{m,1} \\ \vdots \\ w_{m,N(m)-1} \end{bmatrix}. \end{aligned}$$

We remark that the matrix $\textbf{K}$ can be computed directly. We claim that the matrix $\textbf{M}$ also can be computed. Recall that $(\textbf{P}_m)_{m\ge 1}$ is a sequence of compatible $\mu$-partitions of [a, b]. Then (1.2) holds, which implies that the matrix $\textbf{M}$ is completely determined by

$$\begin{aligned} \left\{ \int _{I} x^k\, d\mu :I\in \textbf{P}_1, k=0,1,2\right\} . \end{aligned}$$

(3.5)

Thus the claim holds, since the integrals in (3.6) can be evaluated explicitly for $k=0,1,2$ and $I\in \textbf{P}_1$. Since $\textrm{supp}(\mu )=[a,b]$, $\textbf{M}$ is invertible (see [2, Proposition 3.1]). It follows that the eigenvalues and eigenfunctions of Eq. (3.5) can be solved numerically. $\square$

We remark that numerical algorithms for general eigenproblem as (3.5) have been well developed. We can get good approximations for eigenvalues and eigenfunctions by choosing m sufficiently large (see Theorem 1.3 for details).

We now prove Theorem 1.3. Define the linear map ${{\mathcal {F}}}_m:\textrm{dom}\,{{\mathcal {E}}}\rightarrow S_D^m$ by

$$\begin{aligned} {{\mathcal {F}}}_m u(x)=\sum _{i=1}^{N(m)-1}u(x_{m,i})\phi _{m,i}(x) \qquad u\in \textrm{dom}\,{{\mathcal {E}}} \text{ and } m\ge 1. \end{aligned}$$

We call ${{\mathcal {F}}}_m$ the Rayleigh-Ritz projection with respect to $W_m$. Using [23, Theorem 1.1], we have

$$\begin{aligned} {{\mathcal {E}}}(u-{{\mathcal {F}}}_mu,v)=0 \end{aligned}$$

(3.6)

for all $u\in \textrm{dom}\,{{\mathcal {E}}}$ and $v\in S_D^m$. We remark that

$$\begin{aligned} \Vert u-{{\mathcal {F}}}_mu\Vert _{L^2((a,b),\mu )} \le 2\Vert W_m\Vert ^{1/2}\Vert u\Vert _{\textrm{dom}\,{{\mathcal {E}}}} \end{aligned}$$

(3.7)

for all $u\in \textrm{dom}\,{{\mathcal {E}}}$ and $m\ge 1$ (see [2, Lemma 5.3]), where

$$\begin{aligned} \Vert W_m\Vert :=\max \{|x_{m,i}-x_{m,i-1}|:1 \le i\le N(m)\} \end{aligned}$$

is the norm of $W_m$ for $m\ge 1$. Recall that $E_n$ is the subspace spanned by eigenfunctions $\varphi _1,\cdots ,\varphi _n$ of Eq. (1.1) with $V\equiv 1$. Let $e_n$ be the set of unit vectors in $E_n$ and let

$$\begin{aligned} \sigma _n^{(m)}:=\max _{u\in e_n}\big |2(u,u-{{\mathcal {F}}}_m u)_\mu -(u-{{\mathcal {F}}}_m u,u-{{\mathcal {F}}}_mu)_\mu \big |. \end{aligned}$$

Then provided that $\sigma _n^{(m)}<1$, the approximated eigenvalues are bounded above by

$$\begin{aligned} \hat{\lambda }_n^{(m)}\le \frac{\lambda _n}{1-\sigma _n^{(m)}} \end{aligned}$$

(3.8)

(see [3, Lemma 5.4]).

Proof of Theorem 1.3

We want to estimate $\sigma _n^{(m)}$. Fix any $n\ge 1$ and let $u\in e_n$. Then $\Vert u\Vert _{L^2((a,b),\mu )}=1$ and u can be expressed as $u=\sum _{i=1}^n a_i \varphi _i$, where each $\varphi _i$ is an eigenfunction corresponding to eigenvalue $\lambda _i$. It follows that

$$\begin{aligned} \Vert u\Vert _{\textrm{dom}\,{{\mathcal {E}}}}^2=\sum _{i=1}^n a_i^2 \lambda _i\le \lambda _n\sum _{i=1}^n a_i^2=\lambda _n \Vert u\Vert ^2_{L^2((a,b),\mu )}=\lambda _n. \end{aligned}$$

Combining it with Hölder inequality and (3.8), we have

$$\begin{aligned} \begin{aligned} 2(u,u-{{\mathcal {F}}}_m u)_\mu&\le 2\int _a^b|u(u-{{\mathcal {F}}}_m u)|\, d\mu \le 2 \Vert u\Vert _{L^2((a,b),\mu )}\Vert u-{{\mathcal {F}}}_mu\Vert _{L^2((a,b),\mu )} \\&\le 4\sqrt{\lambda _n}\Vert W_m\Vert ^{1/2} \end{aligned} \end{aligned}$$

(3.9)

for all $m\ge 1$. According to (3.8), (3.9), and (3.10), we have

$$\begin{aligned} \sigma _n^{(m)}\le 4\sqrt{\lambda _n}\Vert W_m\Vert ^{1/2} + 4\lambda _n\Vert W_m\Vert \le M_0r^{m/2}, \end{aligned}$$

where the last inequality used the assumption $\max \{|J|:J\in {\textbf{P}}_k\}\le c\, r^{k}$ for all $k\ge 1$, and $M_0$ is a constant (depending only on n). We first assume that m is sufficiently large so that $\sigma _n^{(m)}<1/2$. Then by (3.9), we get

$$\begin{aligned} \hat{\lambda }_n^{(m)}\le \frac{\lambda _n}{1-\sigma _n^{(m)}}\le \lambda _n (1+ \sigma _n^{(m)}). \end{aligned}$$

Thus there exists a constant $C>0$ (depending only on n) such that for all $m\ge 1$,

$$\begin{aligned} \hat{\lambda }_n^{(m)}\le \lambda _n+Cr^{m/2} \lambda _n. \end{aligned}$$

(3.10)

On the other hand, every eigenvalue is approximated from above(see [3]):

$$\begin{aligned} \hat{\lambda }_n^{(m)}\ge \lambda _n \qquad \text{ for } \text{ all } m. \end{aligned}$$

Together with (3.11), it yields the convergence of the eigenvalues as the first inequality in (1.4). It suffices to prove the convergence of the numerical eigenfunctions.

Let ${{\mathcal {B}}}:=\{\hat{\varphi }_1^{(m)},\cdots , \hat{\varphi }_{N(m)}^{(m)}\}$ be the set of normalized approximate eigenfunctions. Then ${{\mathcal {B}}}$ forms an orthonormal basis for $S_D^m$, which implies

$$\begin{aligned} {{\mathcal {F}}}_m\varphi _n=\sum _{k=1}^{N(m)}({{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})_\mu \hat{\varphi }_k^{(m)}. \end{aligned}$$

(3.11)

We claim that $(\hat{\lambda }_k^{(m)}-\lambda _n)({{\mathcal {F}}}_m \varphi _n, \hat{\varphi }_k^{(m)})_\mu =\lambda _n (\varphi _n-{{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})_\mu$. It suffices to show that

$$\begin{aligned} \hat{\lambda }_k^{(m)}({{\mathcal {F}}}_m \varphi _n, \hat{\varphi }_k^{(m)})_\mu =\lambda _n (\varphi _n,\hat{\varphi }_k^{(m)})_\mu . \end{aligned}$$

Since $\hat{\varphi }_k^{(m)}$ and $\varphi _n$ are eigenfunctions, the two sides of this equation can be rewritten as ${{\mathcal {E}}}({{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})$ and ${{\mathcal {E}}}(\varphi _n,\hat{\varphi }_k^{(m)})$, respectively. It follows from (3.7) that

$$\begin{aligned} {{\mathcal {E}}}({{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})- {{\mathcal {E}}}(\varphi _n,\hat{\varphi }_k^{(m)})={{\mathcal {E}}}({{\mathcal {F}}}_m \varphi _n-\varphi _n, \hat{\varphi }_k^{(m)})=0. \end{aligned}$$

We remark that for any fixed $\lambda _n$, there exists a constant $\gamma >0$ such that for all m sufficiently large,

$$\begin{aligned} \frac{\lambda _n}{|\hat{\lambda }_k^{(m)}-\lambda _n|}\le \gamma \quad \text{ for } \text{ all } \lambda _k\ne \lambda _n. \end{aligned}$$

Then the size of the remaining sum is given by

$$\begin{aligned} \begin{aligned} \Vert {{\mathcal {F}}}_m\varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert ^2_{L^2((a,b),\mu )}&=\sum _{k\ne n} ({{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})^2_\mu =\sum _{k\ne n} \Big (\frac{\lambda _n}{\hat{\lambda }_k^{(m)}-\lambda _n}\Big )^2 (\varphi _n-{{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})^2_\mu \\&\le \gamma ^2\sum _{k\ne n} (\varphi _n-{{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})^2_\mu \le \gamma ^2 \Vert \varphi _n-{{\mathcal {F}}}_m \varphi _n\Vert ^2_{L^2((a,b),\mu )}, \end{aligned} \end{aligned}$$

where the claim has been used in the second equality and $\alpha :=({{\mathcal {F}}}_m \varphi _n,\hat{\varphi }_k^{(m)})_\mu$. It follows that

$$\begin{aligned} \begin{aligned} \Vert \varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}&\le \Vert \varphi _n-{{\mathcal {F}}}_m \varphi _n\Vert _{L^2((a,b),\mu )}+\Vert {{\mathcal {F}}}_m\varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )} \\ {}&\le (1+\gamma )\Vert \varphi _n-{{\mathcal {F}}}_m \varphi _n\Vert _{L^2((a,b),\mu )}. \end{aligned} \end{aligned}$$

(3.12)

Since $\varphi _n$ and $\hat{\varphi }_n$ are normalized eigenfunctions, we have

$$\begin{aligned} |\alpha -1|=\big |\Vert \alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}-\Vert \varphi _n\Vert _{L^2((a,b),\mu )}\big |\le \Vert \varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}. \end{aligned}$$

(3.13)

Combining (3.8), (3.13) and (3.14), we see that

$$\begin{aligned} \begin{aligned} \Vert \varphi _n-\hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}&\le \Vert \varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}+ \Vert \alpha \hat{\varphi }_n^{(m)}-\hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}\\&=\Vert \varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}+ |\alpha -1|\cdot \Vert \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}\\&\le 2 \Vert \varphi _n-\alpha \hat{\varphi }_n^{(m)}\Vert _{L^2((a,b),\mu )}\\&\le 2(1+\gamma )\Vert \varphi _n-{{\mathcal {F}}}_m \varphi _n\Vert _{L^2((a,b),\mu )}\le C r^{m/2}, \end{aligned} \end{aligned}$$

which completes the proof of Theorem  1.3. $\square$

Based on Theorems 1.2 and 1.3, we solve the eigenproblem (1.1) for a class of self-similar measures satisfying (EFT), which is defined by the following family of IFSs:

$$\begin{aligned} S_1(x)=r_1x,\quad S_2(x)=r_2x+r_1(1-r_2),\quad S_3(x)=r_2x+1-r_2, \end{aligned}$$

(3.14)

where $r_1,r_2\in (0,1)$ satisfy $r_1+2r_2-r_1r_2\le 1$, i.e., $S_2(1)\le S_3(0)$. Recently, the self-similar measures defined by IFSs in (3.15) have been studied extensively (see, e.g., [5, 13, 18, 19]). These papers mainly study the multifractal properties and spectral dimension of the corresponding self-similar measures.

Let $\mu$ be a self-similar measure defined by an IFS in (3.15) and a probability vector $(p_i)_{i=1}^3$. In order to define a sequence of compatible $\mu$-partitions of [0, 1], we introduce the definition of an island, which is adopted from [19]. Let ${{\mathcal {M}}}_k:=\{1,2,3\}^k$ for $k\ge 1$. A closed interval $I \subseteq [0,1]$ is called a level-k island with respect to $\{{{\mathcal {M}}}_k\}$ if the following conditions hold:

• (1) there exist some words ${\varvec{i}}_0, {\varvec{i}}_1,\dots ,{\varvec{i}}_n$ in ${{\mathcal {M}}}_k$ such that $S_{{\varvec{i}}_k}(0,1)\cap S_{{\varvec{i}}_{k+1}}(0,1)\ne \emptyset$ for all $k=0,\dots , n-1$, and $I=\bigcup _{k=0}^nS_{{\varvec{i}}_k}([0,1])$;

• (2) for any ${\varvec{j}}\in {{\mathcal {M}}}_k\setminus \{{\varvec{i}}_0,\dots ,{\varvec{i}}_n\}$ and any $k\in \{0,\dots ,n\}$, $S_{{\varvec{j}}}(0,1)\cap S_{{\varvec{i}}_k}(0,1)=\emptyset$.

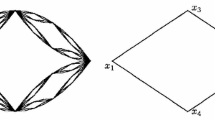
We remark that, $I^\circ$ is a connected component of $S_{{{\mathcal {M}}}_k}(0,1):=\bigcup _{{\varvec{i}}\in {{\mathcal {M}}}_k}S_{{\varvec{i}}}(0,1)$ for all level-k islands I, (see Fig. 1). For $k\ge 1$, define

$$\begin{aligned} {\textbf{P}}_{k}:=\big \{I:I \text{ is } \text{ a } \text{ level-k } \text{ island } \text{ with } \text{ respect } \text{ to } \{{{\mathcal {M}}}_k\} \big \}. \end{aligned}$$

(3.15)

Let $I_{1,1}:=S_1([0,1])\bigcup S_2([0,1])$ and $I_{1,0}:=S_3([0,1])$. Then ${\textbf{P}}_1=\{I_{1,1},I_{1,0}\}$ (see Fig. 1). It is easy to check that $\max \{|I|:I\in {\textbf{P}}_k\}\le |I_{1,1}|\max \{r_1,r_2\}^{k-1}\le (r_1+r_2)^k$ for all $k\ge 1$. Moreover, Ngai and the first author proved that $({\textbf{P}}_k)_{k\ge 1}$ satisfies (1.2) in [26]. Therefore, $(\textbf{P}_k)_{k\ge 1}$ is a sequence of compatible $\mu$-partitions of [0, 1].

Fig. 1

$\mu$-partitions ${\textbf{P}}_k$ for $k=1,2,3$, where ${\textbf{P}}_k$ is defined as in (3.16). Cells that are labeled consist of line segments enclosed by a box. The figure is drawn with $r_1=1/2$ and $r_2=1/3$

If $S_2(1)=S_3(0)$, then $\textrm{supp}(\mu )=[0,1]$. In particular, we let $r_1=1/2$, $r_2=1/3$, and $p_1=p_2=p_3=1/3$. Then we obtain that

$$\begin{aligned} \begin{aligned}&\int _{I_{1,0}}\, d\mu =\frac{1}{3},\qquad{} & {} \int _{I_{1,0}}x\, d\mu =\frac{28}{99},\qquad{} & {} \int _{I_{1,0}}x^2\, d\mu = \frac{8}{33},\\&\int _{I_{1,1}}\, d\mu =\frac{2}{3},\qquad{} & {} \int _{I_{1,1}}x\, d\mu = \frac{26}{99},\qquad{} & {} \int _{I_{1,1}}x^2\, d\mu = \frac{4}{33}, \end{aligned} \end{aligned}$$

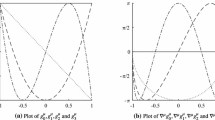
which implies that the mass matrix $\textbf{M}$ can be calculated. Thus Eq. (3.5) can be solved numerically. The numerical result is shown in Fig. 2.

Fig. 2

Normalized eigenfunctions for the self-similar measure defined by the IFS in (3.15) with $r_1=1/2$, $r_2=1/3$ and probability weights $p_1=p_2=p_3=1/3$