1 Introduction

As we know, partial differential equations (PDEs) provide a good way to model the phenomena in real world and their studies have significant applications in many fields such as mathematics, physics, engineering, and so on. A lot of efficient and effective numerical and analytical methods have been developed to study the solutions and their dynamical behaviors. As we know, the classical two-component Drinfel’d-Sokolov-Wilson (DSW) system [1,2,3]

$$\begin{aligned} \left\{ \begin{array}{lc} w_{t}+puu_{x}=0,\\ u_{t}+awu_{x}+buw_{x}+qu_{xxx}=0, \end{array} \right. \end{aligned}$$
(1)

with parameters p, q, a and b, is an important water wave model, which is used to describe the nonlinear surface gravity waves propagating over horizontal seabed. System (1) was originally introduced by Drinfel’d and Sokolov [1, 2] and Wilson [3] from the shallow water wave models. Later, Hirota et al. [4] also derived system (1) from the Kadomtsev–Petviashvili hierarchy. Due to the great applications in physical fields, there have been considerate work concerning the solutions and their dynamics of system (1) and its variants. For example, Hirota et al. [4] provided the soliton structure of system (1). Yao and Li [5] constructed some exact solutions of system (1) through a direct algebra method. Likewise, Liu and Liu [6] presented its four kinds of exact solutions algebraically and revealed their relations. Fan [7] devised an algebraic method to uniformly construct a series of exact solutions of system (1). By improving generalized Jacobi elliptic function method, Yao [8] found some traveling wave solutions of system (1). Doubly periodic wave solutions of system (1) were also constructed through the Adomian decomposition method [9] and an improved F-expansion method [10]. The bifurcation method [11] and the Exp-function method [12] were also employed to derive exact solutions of system (1). Additionally, some methods including the modified kudryashov method [13], the first integral method [14] and the bifurcation method [15, 16] were extended to find abundant exact solutions of fractional DSW system. However, we find that there is little work concerning singularly perturbed DSW system. In fact, in modelling real world problems, such as the shallow water waves in nonlinear dissipative media [17] and dispersive media [18], some relatively weak influences due to uncertainty or perturbation are unavoidable. Therefore, one generally should include certain type of small perturbation to obtain a more realistic model and to better understand its dynamics. Recently, the singularly perturbed models widely appear in modeling the problems across many areas of the natural sciences, and has attracted more and more interest [19,20,21,22,23,24,25,26,27,28,29,30]. Ogawa [19] investigated the persistence of solitary waves and periodic waves of the perturbed KdV equation and Yan et al. [20] further proved the results for a perturbed generalized KdV equation. Further, Chen et al. [22] also considered the persistence of kink and periodic waves for a perturbed defocusing mKdV equation. Chen et al. [21] also obtained the persistence of solitary waves and periodic waves for the perturbed generalized BBM equation. Among most of these work [19,20,21, 23, 24, 26, 27], the authors focused on solitary waves and periodic waves, and little [22, 25] concerned kink waves, especially for the two-component systems. As a matter of fact, kink waves have been found in many important integrable models [31,32,33,34,35,36] including negative–order KdV equation and Camassa–Holm equations, and are believed to have many significant applications in fluid mechanics, nonlinear optics, classical and quantum fields theories etc. Therefore, it is of interest to check whether these kink waves persist under perturbation.

In this paper, we intend to examine the dynamics of the following singularly perturbed two-component DSW system

$$\begin{aligned} \left\{ \begin{array}{lc} w_{t}+puu_{x}=0,\\ u_{t}+awu_{x}+buw_{x}+qu_{xxx}+\varepsilon (u_{xx}+u_{xxxx})=0, \end{array} \right. \end{aligned}$$
(2)

where the parameters \(p<0, a>0, b>0, q>0\), and small \(\varepsilon >0\) standing for the perturbation parameter. In system (2), \(u_{xx}\) and \(u_{xxxx}\) represent the backward diffusion and dissipation terms, respectively. At first glance, one might expect that system (2) should have similar solutions with system (1). As indicated in [19], the answer to this question is significant not only mathematically but also in the application point of view, since in some physical circumstances, for example the Reynolds number is large or surface tension is small, correspond to the case when \(\varepsilon\) is small. Besides, it also helps understand the role of dispersion, dissipation, and instability in nonlinear wave systems. Our aim is to show the persistence of kink and periodic waves with singular perturbation under suitable conditions. To be specific, we first reduce the corresponding high-dimensional system to the perturbed planar system by geometric singular perturbation theory (GSPT). Then we are able to study the wave speed in detail by perturbation analysis and Abelian integrals theory, from which we find the sufficient conditions to guarantee the existence of heteroclinic orbit and periodic orbits, which indicates the existence of kink and periodic waves. Furthermore, we also show that the limit wave speed \(c_0(k)\) is increasing for \(k\in [-\frac{1}{4q},0)\).

2 The reduction of traveling wave system on the slow manifold

In this section, we derive the reduction of traveling wave system corresponding to (2) on the slow manifold by exploiting GSPT.

The transformations

$$\begin{aligned} w(x,t)=\psi (\xi ), u(x,t)=\varphi (\xi ), \ \xi =x-ct, \end{aligned}$$

with \(c>0\), convert system (2) into the following system

$$\begin{aligned} \left\{ \begin{array}{lc} -c\psi '+p\varphi \varphi '=0,\\ -c\varphi '+a\psi \varphi '+b\varphi \psi '+q\varphi '''+\varepsilon \varphi ''+\varepsilon \varphi ''''=0. \end{array} \right. \end{aligned}$$
(3)

The first equation of (3) yields

$$\begin{aligned} \psi =\frac{p}{2c}\varphi ^{2}+g_{1}, \end{aligned}$$

with constant \(g_{1}\). Substituting it into the other equation of (3) yields

$$\begin{aligned} q\varphi ''+\frac{p(a+2b)}{6c}\varphi ^{3}+(ag_{1}-c)\varphi +\varepsilon \varphi '+\varepsilon \varphi '''=0. \end{aligned}$$
(4)

Exploiting the transformations \(\eta =\sqrt{ag_{1}-c}\ \xi\) and \(\varphi =\sqrt{\frac{-6c(ag_{1}-c)}{p(a+2b)}}\phi\), where \(ag_{1}-c>0\), we can rewrite (4) as

$$\begin{aligned} \phi -\phi ^{3}+q\ddot{\phi }+\varepsilon \left( \frac{1}{\sqrt{ag_{1}-c}}\dot{\phi }+\sqrt{ag_{1}-c}\dddot{\phi }\right) =0, \end{aligned}$$
(5)

where dot indicates the derivative with respect to \(\eta\).

System (5) indicates the following singularly perturbed system

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{d \phi }{d \eta }=y,\\ \frac{d y}{d \eta }=z,\\ \varepsilon \sqrt{ag_{1}-c}\frac{d z}{d \eta }=\phi ^{3}-\phi -qz-\frac{\varepsilon }{\alpha }y, \end{array} \right. \end{aligned}$$
(6)

which is called the slow system, and has three equilibrium points \((0,0,0), (-1,0,0)\) and (1, 0, 0).

Introducing the transformation \(\tau =\frac{\eta }{\varepsilon }\), we obtain the following equivalent fast system corresponding to system (6)

$$\begin{aligned} \left\{ \begin{array}{lc} \frac{d \phi }{d\tau }=\varepsilon y,\\ \frac{d y}{d\tau }=\varepsilon z,\\ \sqrt{ag_{1}-c}\frac{d z}{d\tau }=\phi ^{3}-\phi -qz-\frac{\varepsilon }{\sqrt{ag_{1}-c}}y. \end{array} \right. \end{aligned}$$
(7)

Letting \(\varepsilon =0\) in system (6), we obtain the critical manifold

$$\begin{aligned} C_{0}=\left\{ (\phi ,y,z)\in R^{3}|z=\frac{1}{q}\left( \phi ^{3}-\phi \right) \right\} . \end{aligned}$$
(8)

Note that the linearization of the fast system (7) restricted on \(C_{0}\) is given by the following matrix

$$\begin{aligned} \textbf{M}= \begin{bmatrix} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ \dfrac{3\phi ^{2}-1}{\sqrt{ag_{1}-c}} &{} 0 &{} \dfrac{-q}{\sqrt{ag_{1}-c}} \end{bmatrix} \end{aligned}$$

Obviously, the matrix \(\textbf{M}\) has three eigenvalues \(\lambda _1=0, \lambda _2=0\) and \(\lambda _3=\dfrac{-q}{\sqrt{ag_{1}-c}}\), and therefore \(C_0\) is normally hyperbolic. According to GSPT, for \(\varepsilon >0\) sufficiently small, three exists a two-dimensional submanifold \(C_\varepsilon\) of \(R^{3}\) within the Hausdorff distance \(\varepsilon\) of \(C_0\), which is invariant under the flow of system (6).

One can write

$$\begin{aligned} C_\varepsilon =\left\{ (\phi ,y,z)\in R^{3}: z=\frac{1}{q}\left( \phi ^{3}-\phi +Z(\phi ,y,\varepsilon )\right) \right\} , \end{aligned}$$

where \(Z(\phi ,y,\varepsilon )\) depends smoothly on \(\phi ,y,\varepsilon\), and satisfies \(Z(\phi ,y,0)=0\). We can expand \(Z(\phi ,y,\varepsilon )\) in \(\varepsilon\) as follows

$$\begin{aligned} Z(\phi ,y,\varepsilon )=\varepsilon z_1(\phi ,y)+O(\varepsilon ^{2}). \end{aligned}$$

By substituting it into the slow system (6), we can get

$$\begin{aligned} \varepsilon \sqrt{ag_{1}-c} \frac{1}{q}(3\phi ^{2}y-y)+O(\varepsilon ^{2})=-\frac{\varepsilon }{\sqrt{ag_{1}-c}}y-\varepsilon z_1(\phi ,y)+O(\varepsilon ^{2}). \end{aligned}$$

Equating the coefficients of \(\varepsilon\), we can obtain

$$\begin{aligned} z_1(\phi ,y)=\frac{\sqrt{ag_{1}-c}}{q}\left( 1-3\phi ^{2}-\frac{q}{ag_1-c}\right) y. \end{aligned}$$
(9)

Therefore, the dynamics on the slow manifold \(C_\varepsilon\) for system (6) is determined by

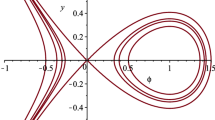
$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d \phi }{d\eta }=y,\\ \frac{d y}{d\eta }=\frac{1}{q}\left( \phi ^{3}-\phi +\varepsilon \frac{\sqrt{ag_{1}-c}}{q}\left( 1-3\phi ^{2}-\frac{q}{ag_1-c}\right) y\right) +O(\varepsilon ^{2}). \end{array}\right. } \end{aligned}$$
(10)

It is easy to check that system (10) with \(\varepsilon =0\) is a Hamiltonian system with the Hamiltonian function

$$\begin{aligned} H(\phi ,y)=-\frac{1}{2}y^{2}-\frac{1}{q}\left( \frac{1}{2}\phi ^{2}-\frac{1}{4}\phi ^{4}\right) , \end{aligned}$$
(11)

and its phase portrait is given in Fig. 1. In addition, we have \(H(0,0)=0\) and \(H(\pm 1,0)=-\frac{1}{4q}\). Then we can parameterize the traveling waves of system (10) with \(\varepsilon =0\) through the curves \(H(\phi ,y)=k\) with parameter k, and display the existence result of traveling wave solutions of system (2) as in the following theorem.

Fig. 1
figure 1

The phase portrait of system (10) with \(\varepsilon =0\)

Full size image
Fig. 2
figure 2

Illustrations of orbits of system (10)

Full size image

Theorem 2.1

For the perturbed two-component DSW system (2), we have the following results.

  1. 1.

    There exists \(\varepsilon _0>0\), \(\varepsilon \in (0,\varepsilon _0)\) and \(k\in [-\frac{1}{4q},0)\), system (2) has a traveling wave

    $$\begin{aligned} u=\sqrt{\frac{-6c(ag_{1}-c)}{p(a+2b)}}\phi (\varepsilon ,h,c,\eta ), \ w=\frac{p}{2c}u^{2}+g_{1}, \end{aligned}$$
    (12)

    where \(c=c(\varepsilon ,k)\), and \(\phi (\varepsilon ,k,c,\eta )\) is the solution of (5).

  2. 2.

    \(c=c(\varepsilon ,k)\) is a smooth function of \(\varepsilon\) and k, with the limit \(c_0(k)\) as \(\varepsilon \rightarrow 0\), where \(c_0(k)\) is a smooth increasing function for \(k\in [-\frac{1}{4q},0)\), moreover,

    $$\begin{aligned} ag_1-\frac{5q}{2}\le c_0(k)\le ag_1-q,~ \lim _{k \rightarrow -1}c_0(k)=ag_1-\frac{5q}{2},~ \lim _{k \rightarrow 0}c_0(k)=ag_1-q. \end{aligned}$$
    (13)
  3. 3.

    When \(\varepsilon \rightarrow 0\), \(\phi (\varepsilon ,k,c,\eta )\) converges to \(\phi (0,k,c_0(h),\eta )\), which is the solution of system (10) with \(\varepsilon =0\), uniformly in \(\eta\).

Remark 1

It is well-known that system (10) with \(\varepsilon =0\) has heteroclinic orbit and a family of periodic orbits, which correspond to kink and periodic waves of system (1) [11], and it is natural to ask whether these heteroclinic orbit and periodic orbits will break up or persist under perturbation in system (2). Theorem 2.1 provides the sufficient conditions about the wave speed to guarantee the persistence of heteroclinic orbit and periodic orbits of system (2), which indicates the existence of kink and periodic waves to system (2).

3 Perturbation Analysis

In this section, we exploit perturbation analysis to check whether the periodic orbits and the heteroclinic orbits persist.

For \((\theta ,0), -1<\theta <0\), let \((\phi (\eta ),y(\eta ))\) be the solution of system (10) with initial point \((\phi ,y)(0)=(\theta ,0)\) (see Fig. 2a). Then there exist \(\eta _1>0\) and \(\eta _2<0\), which satisfy

$$\begin{aligned} y(\eta )>0 ~ for \ 0<\eta <\eta _1,~ y(\eta _1)=0, \end{aligned}$$

and

$$\begin{aligned} y(\eta )<0 ~ for \ \eta _2<\eta <0, ~ y(\eta _2)=0. \end{aligned}$$

Define

$$\begin{aligned} \Phi (\theta ,c,\varepsilon )=\int _{\eta _2}^{\eta _1} \dot{H}(\phi ,y)d\eta =H(\phi (\eta _1),y(\eta _1))-H(\phi (\eta _2),y(\eta _2)), \end{aligned}$$
(14)

where

$$\begin{aligned} \dot{H}(\phi ,y)=-\varepsilon \frac{\sqrt{ag_{1}-c}}{q}\left( 1-3\phi ^{2}-\frac{q}{ag_1-c}\right) y^2+O(\varepsilon ^{2}). \end{aligned}$$

Obviously, \(\Phi (\theta ,c,\varepsilon )=0\) if and only if \(\phi (\eta )\) is a periodic solution of (10). We expand \(\Phi (\theta ,c,\varepsilon )\) in \(\varepsilon\) and obtain

$$\begin{aligned} \Phi (\theta ,c,\varepsilon )=\varepsilon \Phi _1(\theta ,c)+O(\varepsilon ^{2}), \end{aligned}$$

where

$$\begin{aligned} \Phi _1(\theta ,c)&= -\frac{\sqrt{ag_{1}-c}}{q} \int \left( (1-3\phi ^{2}_0)y^{2}_0-\frac{q}{ag_1-c} y^{2}_0\right) d\eta \\&=-\frac{1}{\sqrt{ag_{1}-c}} \left( (ag_1-c)\int (\phi ''_0)^{2} d\eta - \int (\phi '_0)^{2} d\eta \right) , \end{aligned}$$

in which, \((\phi _0, y_0)\) is a solution of system (10) with \(\varepsilon =0\) and this integral is performed on a level curve \(H=H(\theta ,0)\in (-\frac{1}{4q},0)\), since

$$\begin{aligned} \int \phi ^{2}_0 (\phi _0')^{2} d\eta =-\frac{1}{3}\int \phi _0^{3} \phi _0'' d\eta , \end{aligned}$$

and

$$\begin{aligned} \int (\phi _0')^{2} d\eta =- \int \phi _0 \phi _0'' d\eta , \end{aligned}$$

by exploiting integration by parts.

Therefore, \(\Phi _1(\theta ,c)=0\) indicates that the limit speed \(c_0(k)\) satisfies

$$\begin{aligned} c_0(k)=ag_1-\frac{\int (\phi _0')^{2} d\eta }{\int (\phi _0'')^{2} d\eta }. \end{aligned}$$
(15)

We can define the similar function for a heteroclinic orbit as

$$\begin{aligned} \Psi (c,\varepsilon )= \int _{-\infty }^{0} \dot{H}(\phi ,y)d\eta +\int _{0}^{+\infty } \dot{H}(\phi ,y)d\eta , \end{aligned}$$

in which, the first integral is performed along with the solution \((\phi (\eta ), y(\eta ))\) on the one dimensional unstable manifold of the saddle point \((-1,0)\) with \(y(\eta )>0\) for \(-\infty<\eta <0\) and \(y(0)=y_1\), where \(y_1\) is the y coordinate corresponding to the intersection point of the unstable manifold of \((-1,0)\) and the y axis (see Fig. 2b). The later is defined similarly. Following the similar procedure, we also deduce that the limit speed \(c_0(k)\) satisfies (15), where \(\phi _0\) is a solution of system (10) with \(\varepsilon =0\) and the integration is performed on the curve \(H=-\frac{1}{4q}\).

4 Analysis by the Abelian Integral Theory

In this section, we first express the limit speed \(c_0(h)\) in the form of Abelian integrals and then study its properties. Furthermore, we will prove the Theorem 2.1.

Assume that \(\phi (\eta )\) is the solution of system (10) with \(\varepsilon =0\), and Q and R are defined by

$$\begin{aligned} Q=\frac{1}{2} \int (\phi '')^{2} d\eta , \ R=\frac{1}{2} \int (\phi ')^{2} d\eta , \end{aligned}$$

where the integrals are performed along the orbits of system (10).

Introducing a new variable \(h=4qk\), now from (15), we can treat \(c_0(k)\) as a function of h

$$\begin{aligned} c_0(h)=ag_1-\frac{R}{Q}. \end{aligned}$$

Now it is time to analyze Q and R in detail. Suppose that \(\pm \alpha (h)\) and \(\pm \beta (h)\) are four roots of \(\phi ^4-2\phi ^{2}-h=0\), where \(-1\le h<0\), satisfying \(0\le \alpha (h)\le \beta (h)\). Therefore, we can express Q and R as

$$\begin{aligned} Q=\frac{1}{\sqrt{2q^{3}}} \int _{-\alpha (h)}^{\alpha (h)} \frac{(\phi ^{3}-\phi )^{2}}{E(\phi )} d\phi , R=\frac{1}{2\sqrt{2q}} \int _{-\alpha (h)}^{\alpha (h)} E(\phi ) d\phi , \end{aligned}$$
(16)

where \(E(\phi )=\sqrt{\phi ^4-2\phi ^{2}-h}\).

For convenience, we introduce the following integrals:

$$\begin{aligned} J_n(h)=\int _{-\alpha (h)}^{\alpha (h)}\phi ^nE(\phi )\textrm{d}\phi , \ n=0,1,2,\cdots , \end{aligned}$$
(17)

which satisfy

$$\begin{aligned} \int _{-\alpha (h)}^{\alpha (h)}\frac{\phi ^n}{E(\phi )}\textrm{d}\phi =-2J_n'(h), \end{aligned}$$
(18)

by direct calculus. Now we can rewrite Q and R as

$$\begin{aligned} Q=\frac{\sqrt{2}}{\sqrt{q^{3}}}\left( -J'_{6}(h)+2J'_{4}(h)-J'_{2}(h)\right) , \ R=\frac{1}{2\sqrt{2q}}J_0(h). \end{aligned}$$
(19)

To study the monotonicity of \(c_0(h)\), we turn to \(Z(h)=\frac{Q}{R}\), and present its properties in Proposition 4.1.

Proposition 4.1

We have

$$\begin{aligned} Z'(h)>0, and ~ \frac{2}{5q}\le Z(h)\le \frac{1}{q}, ~ \text {for} \ -1<h<0. \end{aligned}$$

Moreover

$$\begin{aligned} \lim _{h \rightarrow -1} Z(h)=\frac{2}{5q},~ and ~ \lim _{h \rightarrow 0} Z(h)=\frac{1}{q}. \end{aligned}$$

To prove Proposition 4.1, we need the following lemmas.

Lemma 4.1

We have

$$\begin{aligned} J_0\left( -1\right) =\frac{4}{3}, J_2\left( -1\right) =\frac{4}{15}, \frac{J_2\left( -1\right) }{J_0\left( -1\right) }=\frac{1}{5}, \text {and} \ \lim _{h \rightarrow 0} \frac{J_2(h)}{J_0(h)}=0. \end{aligned}$$

Proof

Through direct calculus, we have

$$\begin{aligned} J_0\left( -1\right) = \int _{-1}^{1} \sqrt{\phi ^{4}-2\phi ^{2}+1}d\phi = 2\int _{0}^{1} (1-\phi ^{2}) d\phi = \frac{4}{3}, \end{aligned}$$
$$\begin{aligned} J_2\left( -1\right) = \int _{-1}^{1} \phi ^{2} \sqrt{\phi ^{4}-2\phi ^{2}+1}d\phi = 2\int _{0}^{1} \phi ^{2} (1-\phi ^{2}) d\phi = \frac{4}{15}, \end{aligned}$$

and \(\frac{J_2\left( -1\right) }{J_0\left( -1\right) }=\frac{1}{5}\) follows. In addition, by the squeeze theorem, we easily get

$$\begin{aligned} \lim _{h \rightarrow 0} \frac{J_2(h)}{J_0(h)}=\lim _{\phi \rightarrow 0}\phi ^{2}=0. \end{aligned}$$

\(\square\)

Lemma 4.2

We have

$$\begin{aligned} \begin{aligned}&J_0=\frac{4h}{3}J'_0+\frac{4}{3} J'_2,\\&J_2=\frac{4h}{15}J'_0+\frac{4}{15}(3h+4) J'_2,\\&J_4=\frac{h}{7} J_0+\frac{8}{7}J_2,\\&J_6=\frac{4h}{21} J_0+\frac{32+7h}{21}J_2. \end{aligned}\end{aligned}$$
(20)

Proof

Differentiating both sides of \(E^{2}=\phi ^{4}-2\phi ^{2}-h\) with respect to \(\phi\) yields

$$\begin{aligned} E\frac{dE}{d\phi }=2\phi ^{3}-2\phi , \end{aligned}$$

and it follows that

$$\begin{aligned} J_0=&\int _{-\alpha (h)}^{\alpha (h)} E^{2}\frac{d\phi }{E} \\ = {}&\int _{-\alpha (h)}^{\alpha (h)} (\phi ^{4}-2\phi ^{2}-h)\frac{d\phi }{E} \\ = {}&\int _{-\alpha (h)}^{\alpha (h)} \left( \left( \frac{1}{2}E\frac{dE}{d\phi }+\phi \right) \phi -2\phi ^{2}-h\right) \frac{d\phi }{E} \\ = {}&-\frac{1}{2}J_0+2J'_2+2h J'_0, \end{aligned}$$

by integration by parts and (18). Hence, we have

$$\begin{aligned} J_0=\frac{4h}{3}J'_0+\frac{4}{3} J'_2. \end{aligned}$$

Similarly, we have

$$\begin{aligned} J_2=&\int _{-\alpha (h)}^{\alpha (h)} \phi ^{2}E^{2}\frac{d\phi }{E} \\ =&\int _{-\alpha (h)}^{\alpha (h)} \phi ^{2}(\phi ^{4}-2\phi ^{2}-h)\frac{d\phi }{E} \\ =&\int _{-\alpha (h)}^{\alpha (h)} \left( \left( \frac{1}{2}E\frac{dE}{d\phi }+\phi \right) (\phi ^{3}-2\phi )-h\phi ^{2}\right) \frac{d\phi }{E} \\ =&\int _{-\alpha (h)}^{\alpha (h)} \frac{1}{2}\phi ^{3}dE- \int _{-\alpha (h)}^{\alpha (h)} \phi dE+ \int _{-\alpha (h)}^{\alpha (h)} \phi ^{4}\frac{d\phi }{E}- \int _{-\alpha (h)}^{\alpha (h)} 2\phi ^{2}\frac{d\phi }{E}- \int _{-\alpha (h)}^{\alpha (h)} h\phi ^{2}\frac{d\phi }{E} \\ =&\frac{1}{2}J_0-\frac{3}{2}J_2+2J'_2+2hJ'_2, \end{aligned}$$

and it follows that,

$$\begin{aligned} J_2=\frac{4h}{15}J'_0+\frac{4}{15}(3h+4) J'_2. \end{aligned}$$

\(J_4\) and \(J_6\) can be obtained in a similar way. Here we omit them. \(\square\)

From (19) and (20), we see that Q can be expressed by \(J_0'\) and \(J_2'\), which can be inversely expressed by \(J_0\) and \(J_2\) in Lemma 4.3.

Lemma 4.3

We have

$$\begin{aligned} \begin{aligned}&J'_0=\frac{1}{\Delta }\left( \left( \frac{3h}{4}+1\right) J_0-\frac{5}{4}J_2\right) ,\\&J'_2=\frac{h}{4\Delta }\left( - J_0+5J_2\right) ,\\&J''_0=-\frac{1}{4\Delta }\left( hJ'_0+J'_2\right) ,\\&J''_2=-\frac{h}{4\Delta }\left( J'_0+J'_2\right) , \end{aligned}\end{aligned}$$
(21)

where \(\Delta =h(h+1)\).

Proof

This lemma follows from the first two equations in (20) by direct calculation. \(\square\)

Lemma 4.4

We have

$$\begin{aligned} Z(h)=\frac{Q}{R}=\frac{4}{q}\left( \frac{1}{4}-\frac{3}{4}\frac{J_2}{J_0}\right) . \end{aligned}$$
(22)

.

Proof

Exploiting (19) and (21), we easily obtain

$$\begin{aligned} \begin{aligned} \frac{\sqrt{q^{3}}}{\sqrt{2}}Q=&-J'_6(h)+2J'_4(h)-J'_2(h) \\ =&-\frac{4}{21}J_0(h)-\frac{4}{21}hJ'_0(h)-\frac{1}{3}J_2(h)-\frac{1}{21}(32+7h)J'_2(h) +\frac{16}{7}J'_2(h)\\&\quad +\frac{2}{7}J_0(h)+\frac{2}{7}hJ'_0(h)-J'_2(h) \\ =&\frac{2}{21}J_0(h)-\frac{1}{3}J_2(h)+\frac{2h}{21}J'_0(h)-\frac{5+7h}{21}J'_2(h) \\ =&\frac{1}{4}J_0(h)-\frac{3}{4}J_2(h), \end{aligned}\end{aligned}$$
(23)

and the statement follows. \(\square\)

To prove \(Z'(h)>0\) for \(-1<h<0\) in Proposition 4.1, we need to study the monotonicity of \(\frac{J_2}{J_0}\). To state conveniently, introduce the notations

$$\begin{aligned} \tilde{A}=\frac{J_2}{J_0}, \text {and} \ \hat{A}=\frac{J'_2}{J'_0}. \end{aligned}$$

Lemma 4.5

For \(-1<h_0<0\), if \(\tilde{A}'(h_0)=0\), then \(0<\tilde{A}(h_0)<\frac{1}{5}\).

Proof

Eliminating \(J'_0\) from the first two equations of (20), we arrrive at

$$\begin{aligned} J_2-\frac{1}{5}J_0=\frac{4(h+1)}{5}J'_2 \end{aligned}$$

i.e.

$$\begin{aligned} \tilde{A}-\frac{1}{5}=\frac{4(h+1)}{5}\frac{J'_0}{J_0}\hat{A}. \end{aligned}$$

If \(\tilde{A}'(h_0)=0\), then we easily have \(\tilde{A}(h_0)=\hat{A}(h_0)\), and

$$\begin{aligned} \tilde{A}(h_0)-\frac{1}{5}=\frac{4(h_0+1)}{5}\frac{J'_0(h_0)}{J_0(h_0)}\tilde{A}(h_0). \end{aligned}$$

Note that \(\frac{J'_0(h_0)}{J_0(h_0)}<0\) and \(h_0+1>0\), and it follows that

$$\begin{aligned} \tilde{A}(h_0)\left( \tilde{A}(h_0)-\frac{1}{5}\right) <0, \end{aligned}$$

which indicates the statement. \(\square\)

Lemma 4.6

For \(-1\le h\le 0\), we have

$$\begin{aligned} 0\le \tilde{A}(h)\le \frac{1}{5}, \end{aligned}$$
(24)

and

$$\begin{aligned} \frac{2}{5q}\le Z(h)\le \frac{1}{q}. \end{aligned}$$
(25)

Proof

The statements follow easily from Lemmas 4.1, 4.4 and 4.5. \(\square\)

Lemma 4.7

If \(\tilde{A}'(h_0)=0\) for \(-1<h_0<0\), then \(\tilde{A}''(h_0)>0\).

Proof

Differentiating both sides of the equations \(J_2=J_0\tilde{A}\) twice and \(J'_2=J'_0\hat{A}\) once with respect to h, respectively, yields

$$\begin{aligned} J''_2=\tilde{A}''J_0+J''_0\tilde{A}+2J'_0\tilde{A}'=J''_0\hat{A}+J'_0\hat{A}', \end{aligned}$$

and it follows that

$$\begin{aligned} \tilde{A}''(h_0)&=\frac{1}{J_0(h_0)}\left( J''_0(h_0)\hat{A}(h_0)+J'_0(h_0)\hat{A}'(h_0)-2J'_0(h_0)\tilde{A}'(h_0)-J''_0(h_0)\tilde{A}(h_0)\right) \nonumber \\&=\frac{J'_0(h_0)\hat{A}'(h_0)}{J_0(h_0)}, \end{aligned}$$
(26)

since \(\tilde{A}(h_0)=\hat{A}(h_0)\), if \(\tilde{A}'(h_0)=0\). Note that \(J_0>0\) and \(J'_0<0\), therefore, we just need show that \(\hat{A}'(h_0)<0\), which can be proved as follows

$$\begin{aligned} \hat{A}'(h_0)=&\frac{1}{(J'_0(h_0))^{2}}(J''_2(h_0)J'_0(h_0)-J''_0(h_0)J'_2(h_0)) \\ =&-\frac{h_0}{4h_0(h_0+1)}\left( J'_0(h_0)+J'_2(h_0)\right) \frac{1}{J'_0(h_0)}\\&\quad +\frac{1}{4h_0(h_0+1)}\left( h_0J'_0(h_0)+J'_2(h_0)\right) \frac{J'_2(h_0)}{(J'_0(h_0))^2} \\ =&\frac{1}{4h_0(h_0+1)}\left( \hat{A}^{2}(h_0)-h_0\right) , \end{aligned}$$

since \(h_0(h_0+1)<0\) and \(\hat{A}^{2}(h_0)-h_0>0\) for \(-1<h_0<0\). Thus, the proof is completed. \(\square\)

Hence we have the conclusion \(\tilde{A}'(h)=\left( \frac{J_2(h)}{J_0(h)}\right) '<0\) by the proof by contradiction (see Fig. 3 for illustration), based on the facts in Lemmas 4.1 and 4.7, and the following lemma follows from \(Z(h)=\frac{4}{q}\left( \frac{1}{4}-\frac{3}{4}\frac{J_2}{J_0}\right) =\frac{4}{q}\left( \frac{1}{4}-\frac{3}{4}\tilde{A}(h)\right)\).

Fig. 3
figure 3

Illustration of contradiction

Full size image

Lemma 4.8

For \(-1<h_0<0\), \(Z'(h)>0\).

Obviously, the statements in Proposition 4.1 follow from Lemma 4.8. Now we can prove Theorem 2.1.

Since \(\frac{\partial \Phi _1}{\partial c}(\theta ,c_0(k))=\frac{\int (\phi ''_0)^{2} d\eta }{2\sqrt{ag_1-c_0(k)}}+\frac{\int (\phi '_0)^{2} d\eta }{2\sqrt{ag_1-c_0(k)}(ag_1-c_0(k))}>0\), by the implicit function theorem, there exist a unique smooth function \(c_h(\varepsilon )=c(\varepsilon ,h)\) for \(h\in [-1,0]\) and \(\varepsilon \in (0,\varepsilon _0)\) so that

$$\begin{aligned} \tilde{\Phi }(\theta , c(\varepsilon ,h),\varepsilon )= & {} 0 ~ \text {for} -1<h<0,~ 0<\varepsilon<\varepsilon _0, \\ \tilde{\Psi }(c(\varepsilon ,h),\varepsilon )= & {} 0, ~ 0<\varepsilon <\varepsilon _0. \end{aligned}$$

The existence of \(c(\varepsilon ,h)\) indicates the first statement in Theorem 2.1, since \(k=\frac{h}{4q}\). While the second statement in Theorem 2.1 follows from Proposition 4.1, and the third statement holds obviously.

5 Conclusion

Through perturbation analysis and Abelian integrals theory, we derive the sufficient conditions about the wave speed to guarantee the existence of heteroclinic orbit and periodic orbits, which indicates the existence of kink and periodic waves. Besides, we also prove the monotonicity of the limit wave speed \(c_0(k)\). As we know, the wave phenomena, such as the discovery of solitary waves, kink and periodic waves, play an important role in fluid dynamics, plasma and elastic media. We believe that the waves found under small perturbation in a more realistic model will help facilitate the wave dynamics, and it potentially provides a way to analyze the propagation of the nonlinear waves.