Dynamic Transition Analysis for Activator-Substrate System

Abstract

The main objective of this article is to study the dynamic transition associated with the activator-substrate system. Two criteria are derived to describe the transition from real eigenvalues or complex eigenvalues and the types of transition. Notably, we get two parameters $b_{1}$ and $b_{2}$, which can determine the the types of transitions for the two criteria respectively. The analysis is carried out using dynamic transition theory developed recently by Ma and Wang (Phase transition dynamics, Springer, New York, 2013, Bifurcation Theory and Applications, World Scientific, Singapore, 2005, Stability and Bifurcation of Nonlinear Evolutions Equations, Science Press, Beijing, China, 2007).

1 Introduction

Natural patterns are various in shape and form. The development processes of such patterns are complex, and also interesting to researchers. To understand the underlying mechanism for patterns of plants and animals, Turing [4] first proposed the coupled reaction-diffusion equations. It was shown that the stable process could evolve into an instability with diffusive effects. He showed that diffusion could destabilize spatially homogeneous states and cause nonhomogeneous spatial patterns, which accounted for biological patterns in plants and animals. Such instability is frequently called the Turing instability, also known as diffusion-driven instability. Gierer and Meinhardt [5] presented the Gierer-Meinhardt model( Activation-inhibition diffusion system [6, 7]) and activator-substrate system (depletion model) [8, 9], and which was used to describe the Turing instability.

In this article, we consider the bifurcation of activator-substrate system, which was used to describe pigmentation patterns in sea shells [10, 11] and the ontogeny of ribbing on ammonoid shell [12], and the model could be written as follows

$$\begin{aligned} \left\{ \begin{aligned}&u_{t}=d\triangle u-u+u^{2}v, \\ {}&v_{t}=D\triangle v-v-u^{2}v+\sigma , \end{aligned} \right. \end{aligned}$$

(1)

where u(x, t) and v(x, t) represent the population densities of the activator and the substrate at time $t > 0$ and spatial location x respectively. Here, the substrate with concentration v(x, t) could be consumed by activation or some indirect effect of activation, and is supplied at a constant rate. d and D are the diffusion constants of the activator and the substrate respectively. $\sigma$ is the source concentration for the substrate, and the activator-substrate system of interest in present work is confined in a rectangle:

$$\begin{aligned} \Omega = \prod _{j=1}^n [0,L_{j}]. \end{aligned}$$

(2)

There are extensive studies from the mathematical point of view for activator-substrate system, and we refer in particular to [13, 14], and the references therein for studies related to the steady-state solutions, Hopf bifurcation, global structure. Motivated by the above papers, what we are concerned in this paper is to study the dynamical transition for the system (1). The technical method for the analysis is the dynamical transition theory, which has been developed by Ma and Wang [1,2,3]. It is worth noticing that the dynamical transition theory is recently developed to identify the transition states and classify them both dynamically and physically, see [15,16,17,18].

With this method in our disposal, we derive in this article a characterization of dynamic transition of the activator-substrate system. In particular, the analysis in this article shows that the activator-substrate system always undergoes a dynamic transition either to multiple equilibria or to periodic solution, dictated by the sign of the parameters $\lambda _{1}$ and $\lambda _{2}$, where $\lambda _{1}$ and $\lambda _{2}$ are related to the diffusion constants of the substrate D, the source concentration for the substrate $\sigma$ and the k-th eigenvalue of the Laplacian $\rho _{k}$:

$$\begin{aligned}{} & {} \lambda _{1}=\mathop {\min }\limits _{k} \frac{1}{\rho _{k}}\left( 1-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) , \end{aligned}$$

(3)

$$\begin{aligned}{} & {} \lambda _{2}=\mathop {\min }\limits _{k} \frac{D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}+2}{D\rho _{k}^{2}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\rho _{k}}. \end{aligned}$$

(4)

For the case of transitions to multiple equilibria, for $\int _{\Omega }e_{k_{2}}^{3}dx\ne 0$, the transition is either continuous or jump based on the sign of parameter $b_{1}$. In the periodic case (complex eigenvalues ), the types of transitions are determined again by another parameter $b_{2}$. $b_{1}, b_{2}$ are related to the diffusion constants of the substrate D, the source concentration for the substrate $\sigma$ and the k-th eigenvalue of the Laplacian $\rho _{k}$, k-th eigenvector of the Laplacian $e_{k}$, see (24) and (45).

This article is organized as follows: Sect. 2 introduces the abstract operator form and the principle of exchange of stabilities (PES), Sect. 3 studies the dynamic transitions of the activator-substrate system and presents the main results. In Sect. 4, we summarize the conclusions and give the example derived from previous calculations.

2 Mathematical Set-Up

2.1 Basic State and Abstract Operator Form

The equation (1) admits three physically realistic constant steady-state solutions:

$$\begin{aligned} \begin{aligned} U_{1}&=(0,\sigma )^{T},\quad \quad \quad \quad \\ U_{2}&=\left( \frac{\sigma -\sqrt{\sigma ^{2}-4}}{2},\frac{\sigma +\sqrt{\sigma ^{2}+4}}{2}\right) ^{T},\\ U_{3}&=\left( \frac{\sigma +\sqrt{\sigma ^{2}-4}}{2},\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\right) ^{T}. \end{aligned} \end{aligned}$$

(5)

In this paper, we mainly focus on the bifurcation and transition problem of (1) at the steady-state solution $U_{3}$ in (5). For this purpose, we take the transition

$$\begin{aligned} u=u^{'}+\frac{\sigma +\sqrt{\sigma ^{2}-4}}{2},\quad v=v^{'}+\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}. \end{aligned}$$

Omitting the prime, the system (1) is written as

$$\begin{aligned} \left\{ \begin{aligned}&u_{t}=\lambda \triangle u+u+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}v+ (\sigma +\sqrt{\sigma ^{2}-4})uv \\ {}&\quad \quad \quad + \frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}u^{2}+u^{2}v, \\ {}&v_{t}=D\triangle v- \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}v-2u- \frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}u^{2} \\ {}&\quad \quad \quad -(\sigma +\sqrt{\sigma ^{2}-4})uv-u^{2}v. \end{aligned} \right. \end{aligned}$$

(6)

Since we will study the influence of the diffusion constants of the activator-d on the stability of bifurcation, so we select $d=\lambda$ as the control parameter.

For system (6), there are two types of physically-sound boundary conditions: the Dirichlet boundary condition

$$\begin{aligned} U=(u,v)=0\quad \text {on} \quad \partial \Omega , \end{aligned}$$

(7)

and the Neumann boundary condition

$$\begin{aligned} \frac{\partial U}{\partial n}=0\quad \text {on} \quad \partial \Omega . \end{aligned}$$

(8)

$\Omega$ is as in Equ. (2) .

Define the function spaces

$$\begin{aligned}{} & {} H=L^{2}(\Omega , R^{2} ), \\{} & {} H_{1}=\{U\in H^{2}(\Omega , R^{2} )\cap H^{1}_{0}(\Omega , R^{2} )\} \text { for boundary condition }(7) \\{} & {} H_{1}=\{U\in H^{2}(\Omega , R^{2} )\mid \frac{\partial U}{\partial n}\mid _{ \partial \Omega }=0\} \text { for boundary condition } (8). \end{aligned}$$

Define the operators $L_{\lambda }=A_{\lambda }+B$ and $G: H_{1}\rightarrow H$ by

$$\begin{aligned} \begin{aligned}&AU=(\lambda \triangle u, D\triangle v)^{T},\quad \quad \quad \quad \quad \quad \quad \quad \\&BU=(u+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}v, - \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}v-2u )^{T},\\&GU=((\sigma +\sqrt{\sigma ^{2}-4})uv+ \frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}u^{2}+u^{2}v,\quad \quad \quad \\&\quad \frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}u^{2}-(\sigma +\sqrt{\sigma ^{2}-4})uv-u^{2}v)^{T}.\quad \quad \quad \end{aligned} \end{aligned}$$

(9)

Then the Equ. (6) with (7) or (8) can be written in the following abstract form

$$\begin{aligned} \frac{dU}{dt}=L_{\lambda }U+G(U). \end{aligned}$$

(10)

2.2 Linear Theory and Principle of Exchange of Stabilities(PES)

The linearized eigenvalue Equ. (6) are given by

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \triangle u+u+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}v=\beta u, \\ {}&D\triangle v- \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}v-2u=\beta v. \end{aligned} \right. \end{aligned}$$

(11)

with the boundary condition (7) or (8). Let $\rho _{k}$ and $e_{k}$ be the k-th eigenvalue and eigenvector of the Laplacian with either the Dirichlet or the Neumann condition:

$$\begin{aligned} \left\{ \begin{aligned}&\triangle e_{k}=-\rho _{k}e_{k}, \\ {}&e_{k}\mid _{\partial \Omega } =0\quad \text {or} \quad \frac{\partial e_{k}}{\partial n}\mid _{\partial \Omega }=0. \end{aligned} \right. \end{aligned}$$

(12)

Denote by $M_{k}$ the matrix given by

$$\begin{aligned} \begin{pmatrix} -\lambda \rho _{k}+1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \end{aligned}$$

It is clear that all eigenvalues $\beta _{k}^{\pm }$ and eigenvectors $\varphi _{k}^{\pm }$ of (11) satisfy the following equations

$$\begin{aligned} \begin{aligned} \varphi _{k}^{\pm }&=\xi _{k}^{\pm } e_{k}, \\ M_{k} \xi _{k}^{\pm }&=\beta _{k}^{\pm }\xi _{k}^{\pm }. \end{aligned} \end{aligned}$$

(13)

Where $\xi _{k}^{\pm }\in R^{2}$ are the eigenvectors of $M_{k}$. And the eigenvalues $\beta _{k}^{\pm }$ are expressed as

$$\begin{aligned} \begin{aligned}&\beta _{k}^{\pm }= \frac{1}{2}(1-\lambda \rho _{k}-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\&\quad \pm \frac{1}{2}[(1-\lambda \rho _{k}-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2}\quad \quad \quad \quad \quad \quad \quad \quad \\&\quad -4({\lambda D\rho _{k}^{2}}+\lambda \rho _{k} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}-D\rho _{k} +\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}-2)]^{\frac{1}{2}}. \end{aligned} \end{aligned}$$

(14)

Proposition 1

With the above calculation, eigenvectors can be derived and are given in the following two groups

• 1. It is clear that $\beta _{k}^{-}(\lambda )<\beta _{k}^{+}(\lambda )=0$ if and only if

  $$\begin{aligned}{} & {} \lambda =\frac{D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}+2}{D\rho _{k}^{2}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\rho _{k}}, \\{} & {} \lambda <\frac{1}{\rho _{k}}\left(1-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right); \end{aligned}$$

• 2. $\beta _{k}^{\pm }=\pm \alpha _{k}(\lambda )i$ with $\alpha _{k}\ne 0$ if and only if

  $$\begin{aligned}{} & {} \lambda =\frac{1}{\rho _{k}}\left(1-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right), \\{} & {} \lambda <\frac{D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}+2}{D\rho _{k}^{2}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\rho _{k}}, \end{aligned}$$

  Where

  $$\begin{aligned} \alpha _{k}(\lambda )=2\left(\lambda D\rho _{k}^{2}+\lambda \rho _{k} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}-D\rho _{k} +\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}-2\right)^{\frac{1}{2}} \end{aligned}$$

Thus we introduce two critical numbers

$$\begin{aligned}{} & {} \lambda _{1}=\mathop {\min }\limits _{k} \frac{1}{k}\left(1-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}) = \frac{1}{\rho _{k_{1}}}(1-D\rho _{k_{1}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) \end{aligned}$$

(15)

$$\begin{aligned}{} & {} \lambda _{2}=\mathop {\min }\limits _{k} \frac{D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}+2}{D\rho _{k}^{2}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\rho _{k}}. =\frac{D\rho _{k_{2}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}+2}{D\rho _{k2}^{2}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\rho _{k_{2}}} \end{aligned}$$

(16)

Obviously, the following theorem holds true.

Theorem 2

Let $\lambda _{1}$ and $\lambda _{2}$ be the two numbers given by (15) and (16). Then we have the following assertions:

• 1. Let $\lambda _{2}<\lambda _{1}$, and $k_{2}>0$ be the integer such that the minimum is achieved at $k_{2}$ in the definition (16) of $\lambda _{2}$. Then $\beta _{k_{2}}^{+}(\lambda )$ is the first real eigenvalue of (11) near $\lambda =\lambda _{2}$ satisfying that

  $$\begin{aligned} \begin{aligned}&\beta _{k_{2}}^{+}(\lambda )\left\{ \begin{aligned}&<0\quad \quad \text {if}\quad \lambda<\lambda _{2}, \\ {}&=0\quad \quad \text {if} \quad \lambda =\lambda _{2},\quad \quad \quad \quad k_{2} \;\text {is defined by} \;(16), \\ {}&>0\quad \quad \text {if}\quad \lambda >\lambda _{2}, \end{aligned} \right. \\ {}&Re\beta _{j}^{\pm }(\lambda )<0,\quad \quad \forall j\in \mathbb {N} \; \text {and}\; j\ne \beta _{k_{2}}^{+}. \end{aligned} \end{aligned}$$

  (17)

• 2. Let $\lambda _{1}<\lambda _{2}$, and $k_{1}>0$ be the integer such that the minimum is achieved at $k_{1}$ in the definition (15) of $\lambda _{1}$. Then $\beta _{k_{1}}^{+}(\lambda )=\beta _{k_{1}}^{-}(\lambda )$ are a pair of first complex eigenvalues of (11) near $\lambda =\lambda _{1}$ satisfying that

  $$\begin{aligned} \begin{aligned}&{ Re}\beta _{k_{1}}^{+}(\lambda )={ Re}\beta _{k_{1}}^{-}(\lambda )\left\{ \begin{aligned}&<0\quad \quad \text {if}\quad \lambda<\lambda _{1}, \\ {}&=0\quad \quad \text {if} \quad \lambda =\lambda _{1},\quad k_{1}\text { is defined by} \; (15), \\ {}&>0\quad \quad \text {if}\quad \lambda >\lambda _{1}, \end{aligned} \right. \\ {}&Re\beta _{j}^{\pm }(\lambda _{1})<0,\quad \quad \forall j\in \mathbb {N} \; \text {and}\; j\ne k_{1}. \end{aligned} \end{aligned}$$

  (18)

Proposition 3

$\beta _{k_{1}}^{\pm }(\lambda )$are simple complex eigenvalues at $\lambda _{1} (<\lambda _{2})$, and in general, if $\rho _{k_{1}}$ is a simple eigenvalue of (12), then $\beta _{k_{2}}^{+}(\lambda )$ are also simple at $\lambda _{2} (<\lambda _{1})$.

3 Main Results and Proofs

In this section, we will give the main results and proofs which based on the the dynamical transition theory for nonlinear dissipative systems developed by Ma and Wang [1,2,3]. Then, the following theorems will show the types of transitions that the system undergos basing on Theorem 2 .

3.1 Transition from Real Eigenvalues

Here after, we always assume that the eigenvalues $\beta _{k_{2}}^{+}(\lambda )$ in (17) are simple. Based on theorem 3.1, as $\lambda _{2}<\lambda _{1}$ the transition of (10) occurs at $\lambda =\lambda _{2}$, which is from real eigenvalues. Let $\rho _{k_{2}}$ be as in theorem 3.1, and $e_{k_{2}}$ the eigenvector of (12) corresponding to $e_{k_{2}}$ satisfying

$$\begin{aligned} \int _{\Omega } e_{k_{2}}^{3} dx\ne 0. \end{aligned}$$

(19)

Then, under the condition (19), for the system (6) with boundary condition (7) or (8) we have the following transition theorem.

Theorem 4

Let $\lambda _{2}<\lambda _{1}$, Then the system (10) has a transition at $\lambda =\lambda _{2}$, which is mixed. In particular, the system bifurcates on each side of $\lambda =\lambda _{2}$ to a unique branch $U^{\lambda }$ of steady state solution, such that the following assertions hold true:

• 1. On $\lambda <\lambda _{2}$, the bifurcated solution $U^{\lambda }$ is a saddle, and the stable manifold separates the space H into two disjoint open sets $W_{1}^{\lambda }$ and $W_{2}^{\lambda }$ , such that $U=0\in { W_{1}^{\lambda }}$ is an attractor, and the orbits of (10) in $W_{2}^{\lambda }$ are far from $U=0$.

• 2. On $\lambda >\lambda _{2}$, the stable manifold separates the neighbourhood $\mathscr {O}$ of $U=0$ into two disjoint open sets $\mathscr {O}_{1}^{\lambda }$ and $\mathscr {O}_{2}^{\lambda }$, such that the transition is jump in $\mathscr {O}_{1}^{\lambda }$, and is continuous in $\mathscr {O}_{2}^{\lambda }$. The bifurcated solution $U^{\lambda } \in \mathscr {O}_{2}^{\lambda }$ is an attractor such that for any $\varphi \in \mathscr {O}_{2}^{\lambda }$

  $$\begin{aligned} \lim _{t\rightarrow \infty } \Vert U(t,\varphi )-U^{\lambda }\Vert _{H}=0, \end{aligned}$$

  where $U(t,U_{0})$ is the solution of (10) with $U(0, U_{0})=U_{0}$.

• 3. The bifurcated solution $U^{\lambda }$ can be expressed as

  $$\begin{aligned}{} & {} U^{\lambda }=-\frac{1}{C}\beta _{k_{2}}^{+}(\lambda )\xi _{k_{2}}^{+} e_{k_{2}}+o(\beta _{k_{2}}^{+}) \\{} & {} \xi _{k_{2}}^{+}=\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}, \quad -2\right)^{T} \\{} & {} C=\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) \left(D\rho _{k_{2}}+1\right)\cdot \\ {}{} & {} \quad { \frac{\left[\frac{\sigma - \sqrt{\sigma ^{2}-4}}{2}(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})-2\sigma -2\sqrt{\sigma ^{2}-4}\right] \int _{\Omega } e_{k_{2}}^{3} dx}{\left[(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2} -(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2)\right]\int _{\Omega } e_{k_{2}}^{2} dx}}. \end{aligned}$$

Proof

We apply Theorem 2.3.2 in [1] to prove this theorem. Let $\Phi$ be the center manifold function of (10) at $\lambda =\lambda _{2}$. We need to simplify the following expression:

$$\begin{aligned} g(y)=\frac{1}{\langle \varphi _{k_{2}}^{+},\varphi _{k_{2}}^{+*}\rangle } \langle G(y\varphi _{k_{2}}^{+}+\Phi (y)),\varphi _{k_{2}}^{+*}\rangle , \end{aligned}$$

(20)

where $y\in R^{1}$, G is the operator defined by (9), $\varphi _{k_{2}}^{+}$ is the eigenvector corresponding to $\beta _{k_{2}}^{+}(\lambda _{2})=0$, and $\varphi _{k_{2}}^{+*}$ is the conjugate eigenvector, which is the eigenvector of adjoint equation for Eq.(11). And the adjoint equation are given by

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \triangle u^{*}+u^{*}-2v^{*}=\beta u^{*}, \\ {}&D\triangle v^{*}- \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}v^{*}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}u^{*}=\beta v^{*}. \end{aligned} \right. \end{aligned}$$

(21)

By (13)

$$\begin{aligned}{} & {} M_{k}\xi _{k}^{\pm }=\beta _{k}^{\pm }\xi _{k}^{\pm },\quad M_{k}^{T}\xi _{k}^{\pm *}=\beta _{k}^{\pm }\xi _{k}^{\pm *}, \nonumber \\&\quad&\varphi _{k_{2}}^{+}=\xi _{k_{2}}^{+}e_{k_{2}},\quad \varphi _{k_{2}}^{+*}=\xi _{k_{2}}^{+*}e_{k_{2}}. \end{aligned}$$

(22)

$$\begin{aligned}{} & {} \begin{pmatrix} -\lambda _{2} \rho _{k_{2}}+1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -D\rho _{k_{2}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \xi _{k_{2}1}^{+} \\ \xi _{k_{2}2}^{+} \end{pmatrix} =0 \end{aligned}$$

(23)

$$\begin{aligned}{} & {} \begin{pmatrix} -\lambda _{2} \rho _{k_{2}}+1 &{} -2 \\ \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} &{} -D\rho _{k_{2}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \xi _{k_{2}1}^{+*} \\ \xi _{k_{2}2}^{+*} \end{pmatrix} =0 \end{aligned}$$

(24)

By definition of $\lambda _{2}$ and $k_{2}$, we infer from (23) and (24) that

$$\begin{aligned}{} & {} \xi _{k_{2}}^{+}=(\xi _{k_{2}1}^{+},\quad \xi _{k_{2}2}^{+})^{T}=(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}, \quad -2)^{T}, \end{aligned}$$

(25)

$$\begin{aligned}{} & {} \xi _{k_{2}}^{+*}=(\xi _{k_{2}1}^{+*}, \xi _{k_{2}2}^{+*})^{T}=\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}, \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}\right)^{T}, \end{aligned}$$

(26)

By $\Phi (y) =o(\mid y\mid )$, the function g(y) in (20) is rewritten as

$$\begin{aligned} g(y)=\frac{1}{\langle \varphi _{k_{2}}^{+},\varphi _{k_{2}}^{+*}\rangle } \langle G(y\varphi _{k_{2}}^{+}),\varphi _{k_{2}}^{+*}\rangle +o(y^{2}). \end{aligned}$$

By (22)and (25) we see that

$$\begin{aligned} \begin{aligned}&G(y\varphi _{k_{2}}^{+})=\left(y^{2}(-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)\quad \quad \quad \\ {}&\quad +\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\cdot \left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2})e_{k_{2}}^{2}+o(y^{2}\right), \\ {}&\quad -y^{2}\left(-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) \\ {}&\quad +\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\cdot \left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2})e_{k_{2}}^{2}+o(y^{2}) \right )^{T}, \end{aligned} \end{aligned}$$

Thus, we deduce from (22) and (25), (26) that

$$\begin{aligned}{} & {} \langle \varphi _{k_{2}}^{+}, \varphi _{k_{2}}^{+*} \rangle =\left[ \left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) ^{2}\right. \\{} & {} \quad \left. -\left( \sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2\right) \right] \int _{\Omega } e_{k_{2}}^{2} dx, \\{} & {} \langle G(y\varphi _{k_{2}}^{+}), \varphi _{k_{2}}^{+*} \rangle =y^{2}\left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) (D\rho _{k_{2}}+1) \\ {}{} & {} \quad \left[ \frac{\sigma - \sqrt{\sigma ^{2}-4}}{2}\left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) -2\sigma -2\sqrt{\sigma ^{2}-4}\right] \\{} & {} \quad \int _{\Omega } e_{k_{2}}^{3} dx+o(y^{2}). \end{aligned}$$

Therefore the function (20) is given by

$$\begin{aligned} g(y)=Cy^{2}+o(y^{2}). \end{aligned}$$

Where

$$\begin{aligned} \begin{aligned}&C=\left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) (D\rho _{k_{2}}+1)\cdot \\ {}&{\frac{\left[ \frac{\sigma - \sqrt{\sigma ^{2}-4}}{2} \left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) -2\sigma -2\sqrt{\sigma ^{2}-4}\right] \int _{\Omega } e_{k_{2}}^{3} dx}{\left[ \left( D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right) ^{2} -\left( \sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2\right) \right] \int _{\Omega } e_{k_{2}}^{2} dx}}. \end{aligned} \end{aligned}$$

and the theorem follows from Theorem 2.3.2 [1], The proof is completed. $\square$

Remark 1

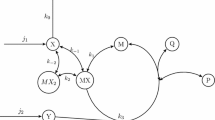
If $\int _{\Omega } e_{k_{2}}^{3} dx\ne 0$, then the local topological structure of the transitions of (10) is schematically shown in the center manifold in Fig. 1.

Fig. 1

Topological structure of mixing transition of (10), when $\int _{\Omega } e_{k_{2}}^{3} dx\ne 0$

Now, we consider the case where (19) is not true, i.e.,

$$\begin{aligned} \int _{\Omega } e_{k_{2}}^{3} dx= 0. \end{aligned}$$

(27)

We introduce the following parameter

$$\begin{aligned} \begin{aligned}&b_{1}=\frac{1}{(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2} -(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2)}\cdot \\ {}&\quad \left(D\rho _{k_{2}}+1)[(\sigma + \sqrt{\sigma ^{2}-4}) ((D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)\int _{\Omega }\psi _{2}e_{k_{2}}^{2}dx \\ {}&\quad +\left(D\rho _{k_{2}}(\sigma -\sqrt{\sigma ^{2}-4})-2\sqrt{\sigma ^{2}-4}\right)\int _{\Omega }\psi _{1}e_{k_{2}}^{2}dx \\ {}&\quad -2\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)^{2} \int _{\Omega }e_{k_{2}}^{4}dx] \end{aligned} \end{aligned}$$

(28)

where $\psi =(\psi _{1},\psi _{2})$ satisfies

$$\begin{aligned} \left\{ \begin{aligned}&\lambda \triangle \psi _{1}+ \psi _{1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \psi _{2}+ [ (D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2}\cdot \\ {}&\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})]e_{k_{2}}^{2}=0 \\ {}&D \triangle \psi _{2}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \psi _{2}-2\psi _{1}- [ (D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2}\cdot \\ {}&\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})]e_{k_{2}}^{2}=0 \end{aligned} \right. \end{aligned}$$

(29)

By the Fredholm Alternative Theorem, under the condition (27), the Equ. (29) has a unique solution.

Then, under the condition (27), we have the second dynamic transition theorem.

Theorem 5

Let (27) hold true, $\lambda _{2}<\lambda _{1}$, and $b_{1}$ is the number given by (28). Then the transition of (10) at $\lambda =\lambda _{2}$ is continuous if $b_{1}<0$, and is jump if $b_{1}>0$. Moreover, the following assertion hold true:

• 1. If $b_{1}>0$, (10) has no bifurcation on $\lambda >\lambda _{2}$, and has exact two bifurcated solutions $U_{+}^{\lambda }$ and $U_{-}^{\lambda }$ on $\lambda <\lambda _{2}$, which are saddles. Moreover, the stable manifolds of the two bifurcated solutions divide the space H into three disjoint open sets $U_{+}^{\lambda }$,$U_{0}^{\lambda }$, $U_{-}^{\lambda }$, such that $U=0\in U_{0}^{\lambda }$ is an attractor, and the orbits of (10) in $U_{\pm }^{\lambda }$ are far from $U=0$.

• 2. If $b_{1}<0$, (10) has no bifurcation on $\lambda <\lambda _{2}$, and has exact two bifurcated solutions $U_{+}^{\lambda }$ and $U_{-}^{\lambda }$ on $\lambda >\lambda _{2}$, which are attractors. In addition, there is a neighbourhood $\mathscr {O}\subset H$ of $U=0$, such that the stable manifold of $U=0$ divides $\mathscr {O}$ two disjoint open sets $\mathscr {O}_{+}^{\lambda }$ and $\mathscr {O}_{-}^{\lambda }$ such that $U_{+}^{\lambda }\subset \mathscr {O}_{+}^{\lambda }$, $U_{-}^{\lambda }\subset \mathscr {O}_{-}^{\lambda }$, and $U_{\pm }^{\lambda }$ attracts $\mathscr {O}_{\pm }^{\lambda }$.

• 3. The bifurcated solution $U_{\pm }^{\lambda }$ can be expressed as

  $$\begin{aligned}{} & {} U_{\pm }^{\lambda }=\pm C (\beta _{k_{2}}^{+}(\lambda ))^{\frac{1}{2}} \xi _{k_{2}}^{+} e_{k_{2}}+o(\beta _{k_{2}}^{+}(\lambda ))^{\frac{1}{2}}, \\{} & {} \xi _{k_{2}}^{+}=\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}, \quad -2\right)^{T}, \\{} & {} C=\left( -\frac{1}{b_{1}}\int _{\Omega }e_{k_{2}}^{2} dx\right) ^{\frac{1}{2}}. \end{aligned}$$

  where $b_{1}$ as in (28).

Proof

We use Theorem 2.3.1 [1] to prove this theorem. To get the function g(y), we need to calculate the center manifold function $\Phi (y)$. By Theorem A1.1 [1], $\Phi (y)$ satisfies

$$\begin{aligned} L_{\lambda _{2}}\Phi =-P_{2}G(y\varphi _{k_{2}}^{+}), \end{aligned}$$

(30)

where $P_{2}:H\rightarrow E_{2}$ is the canonical projection, $L_{\lambda }$ is as in (9), $\varphi _{k_{2}}^{+}$ and $\varphi _{k_{2}}^{+*}$ are given by (22), and

$$\begin{aligned} E_{2}=\{U\in H \mid \langle U,\varphi _{k_{2}}^{+*}\rangle =0\}. \end{aligned}$$

(31)

We see that

$$\begin{aligned} \begin{aligned}&G(y\varphi _{k_{2}}^{+})=\big (y^{2}(-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})\quad \quad \quad \\ {}&\quad +\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\cdot (D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2})e_{k_{2}}^{2}+o(y^{2}), \\ {}&\quad -y^{2}(-2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}) \\ {}&\quad +\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\cdot (D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2})e_{k_{2}}^{2}+o(y^{2}) \big )^{T}, \end{aligned} \end{aligned}$$

Let

$$\begin{aligned} \Phi =\psi y^{2}+o(y^{2}), \quad \quad \psi =(\psi _{1}, \psi _{2} )\in H. \end{aligned}$$

(32)

By (27) and (31), $(e_{k_{2}}^{2},-e_{k_{2}}^{2})\in H$. Hence. it follows from (30) and (32) that

$$\begin{aligned} \begin{aligned}&L_{\lambda }\psi =-[\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}\cdot (D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})^{2} \\ {}&\quad -2(\sigma +\sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})](e_{k_{2}}^{2},-e_{k_{2}}^{2})^{T}. \end{aligned} \end{aligned}$$

(33)

Which is an equivalent form of (29). By (32), we have

$$\begin{aligned} \begin{aligned}&G(y\varphi _{k_{2}}^{+}+\Phi )=G(y\varphi _{k_{2}}^{+}+y^{2}\psi )+o(y^{3}) \\ {}&\quad =\big (y^{3}[(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4})((D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})e_{k_{2}}\psi _{2}-2e_{k_{2}}\psi _{1}) \\ {}&\qquad +(\sigma ^{2}-\sigma \sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})e_{k_{2}}\psi _{1}]+O(y^{2})+o(y^{3}), \\ {}&\qquad -y^{3}[(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4})((D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})e_{k_{2}}\psi _{2}-2e_{k_{2}}\psi _{1}) \\ {}&\qquad +(\sigma ^{2}-\sigma \sqrt{\sigma ^{2}-4})(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})e_{k_{2}}\psi _{1}]+O(y^{2})+o(y^{3}) \big )^{T} \end{aligned} \end{aligned}$$

(34)

Hence, we deduce from (22), (25) and (34) that

$$ \langle G(y\varphi _{{k_{2} }}^{ + } + \Phi ),\varphi _{{k_{2} }}^{{ + *}} \rangle = y^{3} (D\rho _{{k_{2} }} + 1)[(\sigma + \sqrt {\sigma ^{2} - 4} )\left( {D\rho _{{k_{2} }} + \frac{{\sigma ^{2} + \sigma \sqrt {\sigma ^{2} - 4} }}{2}} \right)\int_{\Omega } {\psi _{2} } e_{{k_{2} }}^{2} dx + (D\rho _{{k_{2} }} (\sigma - \sqrt {\sigma ^{2} - 4} ) - 2\sqrt {\sigma ^{2} - 4} )\int_{\Omega } {\psi _{1} } e_{{k_{2} }}^{2} dx\quad - 2\left( {D\rho _{{k_{2} }} + \frac{{\sigma ^{2} + \sigma \sqrt {\sigma ^{2} - 4} }}{2}} \right)^{2} \int_{\Omega } {e_{{k_{2} }}^{4} } dx] + o(y^{3} ).{\text{ }} $$

(35)

Thus, the function g(y) in (20) can be written as

$$\begin{aligned} g(y)=\frac{b_{1}}{\int _{\Omega }e_{k_{2}}^{2}dx}y^{3}+o(y^{3}), \end{aligned}$$

where $b_{1}$ is as in (28). Hence the theorem follows from Theorem 2.3.1 in [1]. $\square$

Remark 2

If $\int _{\Omega } e_{k_{2}}^{3} dx = 0$, then the local topological structure of the transition of (10) is schematically shown in the center manifold in Fig 2 and  3.

Fig. 2

Topological structure of continous transition of (10), when $b_{1}>0$ and $\int _{\Omega } e_{k_{2}}^{3} dx= 0$

Fig. 3

Topological structure of continous transition of (10), when $b_{1}<0$ and $\int _{\Omega } e_{k_{2}}^{3} dx= 0$

Remark 3

When the domain $\Omega$ is a rectangle, i.e. $\Omega =\mathop {\Pi }\limits _{j=1}^{n}(0,L_{j})$, the $b_{1}$ in (28) for the Neumann condition can be explicitly expressed in terms of the parameters $D, \sigma$ and $L_{j}$.

For example, we consider the case where $\Omega =(0,L)$. The eigenvalues $\rho _{k}$ and eigenvectors $e_{k}$ of (12) are given by

$$\begin{aligned} \rho _{k}=\frac{(k-1)^{2}\pi ^{2}}{L^{2}},\quad e_{k}=cos\frac{(k-1)\pi }{L}x,\quad k=1,2,3,\cdot \cdot \cdot . \end{aligned}$$

It is clear that $k_{2}\ge 2$, and (27) hold true. We see that

$$\begin{aligned} e_{k}^{2}=cos^{2}\frac{(k_{2}-1)\pi }{L}x=\frac{1}{2}(1+cos\frac{2(k_{2}-1)\pi }{L})=\frac{1}{2}(e_{1}+e_{2k_{2}-1}). \end{aligned}$$

Hence, by (29), we have

$$\begin{aligned} \psi =\xi e_{1}+\eta e_{j},\quad \quad \text {with} \quad j=2k_{2}-1. \end{aligned}$$

(36)

where

$$\begin{aligned}{} & {} \begin{pmatrix} 1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \xi _{1}\\ \xi _{2} \end{pmatrix} = \begin{pmatrix} -\frac{B}{2}\\ \frac{B}{2} \end{pmatrix} \\{} & {} \begin{pmatrix} -\lambda _{2} \rho _{2k_{2}-1}+1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -D\rho _{2k_{2}-1}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \eta _{1}\\ \eta _{2} \end{pmatrix} = \begin{pmatrix} -\frac{B}{2}\\ \frac{B}{2} \end{pmatrix}\\{} & {} B=\left(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \right) \left(D\rho _{k_{2}}\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}-2\sqrt{\sigma ^{2}-4}-\sigma\right ). \end{aligned}$$

It is readily to see that

$$\begin{aligned}{} & {} \xi _{1}=\frac{B}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-4}, \\{} & {} \xi _{2}=\frac{-B}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-4}, \\{} & {} \eta _{1}=\frac{B}{4} \left(\frac{D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-\left(1-\lambda _{2}\rho _{2k_{2}-1}\right) \left(D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)} -1\right), \\{} & {} \eta _{2}=\frac{1+\lambda _{2}\rho _{2k_{2}-1}}{2\left(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4})-(1-\lambda _{2}\rho _{2k_{2}-1})(2D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)} \end{aligned}$$

Inserting (52) and $\xi _{1}$, $\xi _{2}$, $\eta _{1}$, $\eta _{2}$ into (28), we can get the explicit expression of $b_{1}$.

3.2 Transition from Complex Eigenvalues

As $\lambda _{1}<\lambda _{2}$, the transition of (10) occurs at $\lambda =\lambda _{1}$, and the system bifurcates to a periodic solution.

In this case,

$$\begin{aligned} \lambda _{1}=\mathop {\min }\limits _{\rho _{k}} \frac{1}{\rho _{k}}\left(1-D\rho _{k}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)= \frac{1}{\rho _{k_{1}}}\left(1-D\rho _{k_{1}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right), \end{aligned}$$

Then we define the following parameter $b_{1}$ as in (49). Here $M_{k}$ is the matrix defined by

$$\begin{aligned} M_{k}= \begin{pmatrix} -\lambda _{1}\rho _{k_{1}}+1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2}-1 \\ -2&{} -D\rho _{k_{1}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \end{aligned}$$

(37)

and we have the following theorem

Theorem 6

Let $b_{2}$ be the number given by (49) and $\lambda _{1}<\lambda _{2}$. For the problem (10), the following assertions hold true

• 1. The problem undergoes a dynamic transition at $\lambda =\lambda _{1}$, which is the Hopf bifurcation.

• 2. When $b_{2}<0$, the transition bifurcates to a stable periodic solution on $\lambda >\lambda _{1}$, and when $b_{2}>0$, transition bifurcates to an unstable periodic solution on $\lambda <\lambda _{1}$.

• 3. The bifurcated periodic solution $U^{\lambda }=(U_{1}^{\lambda },U_{2}^{\lambda })$ can be expressed as

  $$\begin{aligned} \begin{aligned}&U_{1}^{\lambda }=\sqrt{2}(-\frac{\gamma }{b_{1}})^{\frac{1}{2}}\sin (\alpha _{0}t+\frac{\pi }{4})e_{k_{1}}+o(\mid \gamma \mid ^{\frac{1}{2}}), \\ {}&U_{2}^{\lambda }=\sqrt{2(\alpha _{0}^{2}+(D\rho _{k_{1}}+\varepsilon ))^{2}} (-\frac{\gamma }{b_{1}})^{\frac{1}{2}}\cos (\alpha _{0}t+\theta )e_{k_{1}}+o(\mid \gamma \mid ^{\frac{1}{2}}), \end{aligned} \end{aligned}$$

  where $\theta =\arctan \frac{\alpha _{0}+D\rho _{k_{1}}+\varepsilon }{\alpha _{0}-D\rho _{k_{1}}-\varepsilon }$.

Proof

By (13) the eigenvalues and eigenvectors of (11) with (7) or (8) at $\lambda _{1}=\frac{1}{\rho _{k_{1}}}\left(1-D\rho _{k_{1}}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}\right)$ are determined by the matrices $M_{k}$ given by (37). It is clear that $M_{k_{1}}$ has a pair of imaginary eigenvalues

$$\begin{aligned} \beta _{k_{1}}^{\pm }(\lambda _{k_{1}})=\pm i \alpha _{0}, \end{aligned}$$

where $\alpha _{0}=[\lambda D\rho _{k_{1}}^{2}+ \lambda \rho _{k_{1}}-D\rho _{k_{1}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}-2 ]^{\frac{1}{2}}.$ It is clear that $\alpha _{0}^{2}=2(\varepsilon -1)-(D\rho _{k_{1}}+\varepsilon )^{2}$, where $\varepsilon =\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}.$ Let $\overline{\xi }, \overline{\eta }\in R^{2}$ be the eigenvectors of $M_{k_{1}}$ satisfying

$$\begin{aligned} M_{k_{1}}\overline{\xi }=\alpha _{0}\overline{\xi },\quad M_{k_{1}}\overline{\eta }=-\alpha _{0}\overline{\eta }. \end{aligned}$$

Then, by (13) the eigenvectors of (11) corresponding to$\beta _{k_{1}}^{\pm }(\lambda _{k_{1}})$ are given by $\xi = \overline{\xi } e_{k_{1}}$, and $\eta =\overline{\eta } e_{k_{1}}.$ It is readily to check that

$$\begin{aligned}{} & {} \xi =(\xi _{1},\xi _{2})=(\varepsilon -1, \alpha _{0}-D\rho _{k_{1}}-\varepsilon )e_{k_{1}}, \end{aligned}$$

(38)

$$\begin{aligned}{} & {} \eta =(\eta _{1},\eta _{2})=(\varepsilon -1,-(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ))e_{k_{1}}. \end{aligned}$$

(39)

We consider the conjugate eigenvectors $\xi ^{*}=\overline{\xi ^{*}}e_{k_{1}}$ and $\eta ^{*}=\overline{\eta ^{*}}e_{k_{1}}$ with

$$\begin{aligned} M_{k_{1}}^{*}\overline{\xi }^{*}=\alpha _{0} \overline{\eta }^{*},\quad \quad M_{k_{1}}\overline{\eta }^{*}=-\alpha _{0}\overline{\xi }^{*}. \end{aligned}$$

where $M_{k_{1}}^{*}$ is the transpose of $M_{k_{1}}$, Direct calculation shows that

$$\begin{aligned}{} & {} \xi ^{*}=(\xi _{1}^{*},\xi _{2}^{*})=(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ,\varepsilon -1)e_{k_{1}}, \end{aligned}$$

(40)

$$\begin{aligned}{} & {} \eta ^{*}=(\eta _{1}^{*},\eta _{2}^{*})=(-\alpha _{0}+D\rho _{k_{1}}+\varepsilon ,\varepsilon -1)e_{k_{1}}. \end{aligned}$$

(41)

It is easy to see that

$$\begin{aligned} \begin{aligned}&\langle \xi , \eta ^{*} \rangle =\langle \eta , \xi ^{*} \rangle =0, \\ {}&\langle \xi , \xi ^{*}\rangle =\langle \eta , \eta ^{*} \rangle =2\alpha _{0}(\varepsilon -1)\int _{\Omega } e_{k_{1}}^{2}dx. \end{aligned} \end{aligned}$$

(42)

Let $U=x\xi +y\eta +\Phi (x,y)\in H$ be a solution of (6) at $\lambda =\lambda _{1}$, and $\Phi$ be the center manifold function. By (42), the reduced Equ. (6) read

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=-\alpha _{0}y+\frac{1}{\langle \xi , \xi ^{*}\rangle }\langle G(x\xi +y\eta +\Phi (x,y)),\xi ^{*} \rangle , \\ {}&\frac{dy}{dt}=\alpha _{0}x+\frac{1}{\langle \eta , \eta ^{*}\rangle }\langle G(x\xi +y\eta +\Phi (x,y)),\eta ^{*} \rangle , \end{aligned} \right. \end{aligned}$$

(43)

where the operator G is given by

$$\begin{aligned} G(u)=G_{2}(u)+G_{3}(u), \end{aligned}$$

(44)

$G_{k}(k=2,3)$ is a k-multilinear operator defined by

$$\begin{aligned} \begin{aligned}&G_{2}(U,V)=\left(\frac{2\varepsilon }{\sigma }u_{1}v_{2}+\frac{\sigma }{\varepsilon }u_{1}v_{1}, -\frac{2\varepsilon }{\sigma }u_{1}v_{2}-\frac{\sigma }{\varepsilon }u_{1}v_{1}\right), \\ {}&G_{3}(U,V,W)=(u_{1}v_{1}w_{2}, -u_{1}v_{1}w_{2}), \\ {}&G_{2}(U)=G_{2}(U,U), \\ {}&G_{3}(U)=G_{3}(U,U,U). \end{aligned} \end{aligned}$$

(45)

Based on (38-42) and (44,45, 43) can be rewritten as

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=-\alpha _{0}y+a_{20}x^{2}+a_{02}y^{2}+a_{11}xy+a_{30}x^{3}+a_{21}x^{2}y+ \\ {}&\quad \quad \quad a_{12}xy^{2}+a_{03}y^{2}+ \frac{x}{\langle \xi , \xi ^{*}\rangle } \langle G_{2}(\xi ,\Phi )+ G_{2}(\Phi ,\xi ), \xi ^{*} \rangle \\ {}&\quad \quad \quad +\frac{y}{\langle \xi , \xi ^{*}\rangle }\langle G_{2}(\eta ,\Phi )+ G_{2}(\Phi ,\eta ), \xi ^{*} \rangle +o(x^{3}+y^{3}), \\ {}&\frac{dy}{dt}=\alpha _{0}x+b_{20}x^{2}+b_{02}y^{2}+b_{11}xy+b_{30}x^{3}+b_{21}x^{2}y+ \\ {}&\quad \quad \quad b_{12}xy^{2}+b_{03}y^{2}+ \frac{x}{\langle \eta , \eta ^{*}\rangle } \langle G_{2}(\xi ,\Phi )+ G_{2}(\Phi ,\xi ),\eta ^{*} \rangle \\ {}&\quad \quad \quad +\frac{y}{\langle \eta , \eta ^{*}\rangle }\langle G_{2}(\eta ,\Phi )+ G_{2}(\Phi ,\eta ), \eta ^{*} \rangle +o(x^{3}+y^{3}), \end{aligned} \right. \end{aligned}$$

(46)

where $a_{20},,a_{11},a_{02},a_{03},a_{21},a_{12},a_{30}$ and $b_{20},,b_{11},b_{02},b_{03},b_{21},b_{12},a_{30}$ are given in Appendix A

We are now in a position to derive the center manifold function $\Phi$. By Theorem A1.1 [1]

$$\begin{aligned} \Phi =\Phi _{1}+\Phi _{2}+\Phi _{3}+o(x^{2}+y^{2}), \end{aligned}$$

(47)

Where

$$\begin{aligned} \begin{aligned}&-L_{\lambda _{1}}\Phi _{1}=P_{2}[G_{2}(\xi ,\xi )x^{2}+(G_{2}(\xi ,\eta )+G_{2}(\eta ,\xi ))xy+G_{2}(\eta ,\eta )y^{2}], \\ {}&-(L_{\lambda _{1}}^{2}+4\alpha _{0}^{2})L_{\lambda _{1}}\Phi _{2}=2\alpha _{0}^{2}P_{2}[(G_{2}(\xi ,\xi )-G_{2}(\eta ,\eta ))(y^{2}-x^{2})\\&\quad -2(G_{2}(\xi ,\eta )+G_{2}(\eta ,\xi ))xy], \\ {}&(L_{\lambda _{1}}^{2}+4\alpha _{0}^{2})\Phi _{3}=\alpha _{0}P_{2}[(G_{2}(\xi ,\eta )+G_{2}(\eta ,\xi ))(y^{2}-x^{2}) +2(G_{2}(\xi ,\xi )\\&\quad -G_{2}(\eta ,\eta ))xy]. \end{aligned} \end{aligned}$$

$L_{\lambda }$ is as in (9), where $P_{2}:H\rightarrow E_{2}$ is the canonical projection, and $E_{2}=\{u\in H\mid \langle u, \xi ^{*} \rangle =\langle u, \eta ^{*}\rangle =0\}$ is the complement of $E_{1}=$ span$\{\xi ,\eta \}$ in H. Note that $\varphi _{k_{k}}^{+},\varphi _{k_{k}}^{+*}$ are given by (22). Hence, we obtain from (38,39,44 and 47).

$$\begin{aligned} \begin{aligned}&\Phi _{1}=(\varepsilon -1)[(\frac{2\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-\varepsilon ) +\frac{\sigma }{\varepsilon } (\varepsilon -1))x^{2}+2(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))xy \\ {}&\quad +(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon +\alpha _{0}))y^{2}]\times \sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx} (-M_{k})^{-1} \begin{pmatrix} 1 \\ -1\end{pmatrix} e_{k}, \\ {}&\Phi _{2}=8\alpha _{0}^{2}(\varepsilon -1)[\frac{\varepsilon }{\sigma }\alpha _{0}(y^{2}-x^{2})-(\sigma (1-\frac{1}{\varepsilon }) -\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))xy] \\ {}&\quad \times \sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx} (-M_{k})^{-1}(M_{k}^{2}+4\alpha _{0}^{2})^{-1} \begin{pmatrix} 1 \\ -1\end{pmatrix} e_{k}, \\ {}&\Phi _{3}=2(\varepsilon -1)[(\sigma (1-\frac{1}{\varepsilon })-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))(y^{2}-x^{2}) +\frac{4\varepsilon }{\sigma }\alpha _{0}xy] \\ {}&\quad \times \sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx} (M_{k}^{2}+4\alpha _{0}^{2})^{-1} \begin{pmatrix} 1 \\ -1\end{pmatrix} e_{k}. \end{aligned} \end{aligned}$$

Direct calculation shows that

$$\begin{aligned} \begin{aligned}&(-M_{k})^{-1}=\frac{1}{det(-M_{k})} \begin{pmatrix} D\rho _{k_{1}}+\varepsilon &{} \varepsilon -1 \\ -2 &{}\lambda _{1}\rho _{k_{1}}-1 \end{pmatrix}, \\&\quad (M_{k}^{2}+4\alpha _{0}^{2})^{-1}=\frac{1}{det(M_{k}^{2}+4\alpha _{0}^{2}) } \times \\ {}&\quad \begin{pmatrix} (D\rho _{k_{1}}+\varepsilon )^{2}-2( \varepsilon -1 )+4\sigma ^{2} &{} -(\varepsilon -1) (1-\lambda _{1}\rho _{k_{1}}-D\rho _{k_{1}}-\varepsilon ) \\ 2(1-\lambda _{1}\rho _{k_{1}}-D\rho _{k_{1}}-\varepsilon ) &{} (1-\lambda _{1}\rho _{k_{1}})^{2}-2(\varepsilon -1)+4\sigma ^{2} \end{pmatrix}, \end{aligned} \end{aligned}$$

Thus we have

$$\begin{aligned} \begin{aligned}&\Phi _{1}=(\varepsilon -1)[(\frac{2\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-\varepsilon ) +\frac{\sigma }{\varepsilon } (\varepsilon -1))x^{2}\\&\quad +2(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))xy \\ {}&\quad +(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon +\alpha _{0}))y^{2}] \begin{pmatrix} E_{1} \\ F_{1}\end{pmatrix}, \\ {}&\Phi _{2}=8\alpha _{0}^{2}(\varepsilon -1)[\frac{\varepsilon }{\sigma }\alpha _{0}(y^{2}-x^{2})-(\sigma (1-\frac{1}{\varepsilon }) -\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))xy] \begin{pmatrix} E_{2} \\ F_{2}\end{pmatrix}, \\ {}&\Phi _{3}=2(\varepsilon -1)[(\sigma (1-\frac{1}{\varepsilon })-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon ))(y^{2}-x^{2}) +\frac{4\varepsilon }{\sigma }\alpha _{0}xy] \begin{pmatrix} E_{3} \\ F_{3}\end{pmatrix}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned}&E_{1}=\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(-M_{k})}\cdot (D\rho _{k}+1) e_{k}, \\ {}&F_{1}=-\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(-M_{k})}\cdot (\lambda _{1}\rho _{k}+1) e_{k}, \\ {}&E_{2}=\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(-M_{k})\cdot det(M_{k}^{2}+4\alpha _{0}^{2})}\cdot [(D\rho _{k}+\varepsilon )A_{k}+(\varepsilon -1)B_{k} ]e_{k}, \\&F_{2}=\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(-M_{k})\cdot det(M_{k}^{2}+4\alpha _{0}^{2})}\cdot [-2A_{k}+(\lambda _{1}\rho _{k}-1)B_{k} ]e_{k}, \\ {}&E_{3}=\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(M_{k}^{2}+4\alpha _{0}^{2})}\cdot A_{k}e_{k}, \\ {}&F_{3}=\sum _{k\ne k_{1}} \frac{\int _{\Omega }e_{k_{1}}^{2}e_{k}dx}{\int _{\Omega }e_{k_{1}}^{2}dx\cdot det(M_{k}^{2}+4\alpha _{0}^{2})}\cdot B_{k} e_{k}, \\ {}&A_{k}=(D\rho _{k}+\varepsilon )^{2}-2(\varepsilon -1)+4\sigma ^{2}+(\varepsilon -1)(1-\lambda _{1}\rho _{k}-D\rho _{k}-\varepsilon ), \\ {}&B_{k}=-2\rho _{k}(\lambda _{1}+D)-(1-\lambda _{1}\rho _{k})^{2}-4\sigma ^{2}. \end{aligned} \end{aligned}$$

Inserting $\Phi =\Phi _{1}+\Phi _{2}+\Phi _{3}+o(x^{2}+y^{2})$ into (46), we derive that

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=-\alpha _{0}y+\sum _{2\le i+j\le 3}a_{ij}x^{i}y^{j}+\sum _{k+r=3}\widetilde{a}_{kr}x^{k}y^{r} +o(x^{3}+y^{3}), \\ {}&\frac{dy}{dt}=\alpha _{0}x++\sum _{2\le i+j\le 3}b_{ij}x^{i}y^{j}+\sum _{k+r=3}\widetilde{b}_{kr}x^{k}y^{r} +o(x^{3}+y^{3}), \end{aligned} \right. \end{aligned}$$

(48)

Where $a_{ij}$ and $b_{ij} (0\le i,j\le 3)$ are as in (46), and $\widetilde{a}_{30}$ are as in Appendix B.

Then we give the number

$$\begin{aligned} \begin{aligned}&{ b_{2}}=\frac{\pi }{2\alpha _{0}}(a_{02}b_{02}-a_{20}b_{20})+\frac{\pi }{4\alpha _{0}}(a_{11}a_{20}+a_{11}a_{02}-b_{11}b_{20}-b_{11}b_{02}) \\ {}&\quad \quad +\frac{3\pi }{4}(a_{30}+b_{30}+\widetilde{a}_{30}+\widetilde{b}_{30})+\frac{\pi }{4}(a_{12}+b_{21}+\widetilde{a}_{12}+\widetilde{b}_{21}), \end{aligned} \end{aligned}$$

(49)

Thus, Assertions (1) and (2) of this theorem follow from Theorem 2.3.7 [1] It is known that the bifurcated periodic solution near $\lambda =\lambda _{1}$ takes form

$$\begin{aligned} U^{\lambda }=x(t)\xi +y(t)\eta +o(| x|+| y|), \end{aligned}$$

(50)

where $\xi$, $\eta$ are as in (38) and (39), and x(t), y(t) are the solutions of the following equation

$$\begin{aligned} \left\{ \begin{aligned}&\frac{dx}{dt}=\gamma (\lambda )x-\alpha _{0}y+\frac{1}{\langle \xi _{\lambda }, \xi _{\lambda }^{*}\rangle }\langle G(x\xi _{\lambda }+y\eta _{\lambda }+\Phi _{\lambda }(x,y)),\xi _{\lambda }^{*} \rangle , \\ {}&\frac{dy}{dt}=\gamma (\lambda )x+\alpha _{0}x+\frac{1}{\langle \eta _{\lambda }, \eta _{\lambda }^{*}\rangle }\langle G(x\xi _{\lambda }+y\eta _{\lambda }+\Phi (x,y)),\eta _{\lambda }^{*} \rangle , \end{aligned} \right. \end{aligned}$$

where $\xi _{\lambda }, \eta _{\lambda }$ are eigenvectors of $L_{\lambda }$ corresponding to the complex eigenvalues $\beta _{k_{0}}^{\pm }(\lambda )$, and $\xi _{\lambda }^{*}, \eta _{\lambda }^{*}$ the conjugate eigenvectors. The solution (x(t), y(t)) near $\lambda _{1}$ is of the form

$$\begin{aligned} \begin{aligned}&x(t)=(-\frac{\gamma }{b_{1}})^{\frac{1}{2}}\cos \alpha _{0}t+o(\mid \gamma \mid ^{\frac{1}{2}}), \\ {}&y(t)=(-\frac{\gamma }{b_{1}})^{\frac{1}{2}}\sin \alpha _{0}t+o(\mid \gamma \mid ^{\frac{1}{2}}), \end{aligned} \end{aligned}$$

(51)

where $b_{1}$ is as in (49). Therefore, assertion (3) holds true from (50), (51). The proof is completed. $\square$

4 Conclusions and examples

In this work, we study the dynamical transition for a activator-substrate system from the perspective of dynamic transition recently developed by Ma and Wang. By using the Principle of Exchange of Stabilities condition for activator-substrate system, we note that the system is in a static state in space patterns for $\lambda <\min \{\lambda _{1},\lambda _{2}\}$, where $\lambda _{1}$ and $\lambda _{2}$ are determined by parameters ${(\sigma , d)} \in R^{2}$ and $\lambda =d$ is the diffusion constant of the activator. However, when $\lambda >\min \{\lambda _{1},\lambda _{2}\}$, i.e., the diffusion constants are greater than the specified value, the stability is broken. Then we have the following characteristics:

First, when $\lambda _{1}>\lambda _{2}$, it was demonstrated that chaotic coexistence bifurcates from the periodic when $\int _{\Omega }e_{k_0}^3dx\ne 0$. If $\int _{\Omega }e_{k_0}^3dx= 0$, we show that the permanent coexistence was existed for activator-substrate system.

Second, when $\lambda _{1}<\lambda _{2}$, the first eigenvalues are complex, and we show that the system undergoes a dynamic transition, which is Hopf bifurcation.

Remark 4

When the domain $\Omega$ is a rectangle, i.e. $\Omega =\mathop {\Pi }\limits _{j=1}^{n}(0,L_{j})$, the $b_{1}$ in Theorem 3.2 for the Neumann condition can be explicitly expressed in terms of the parameters $D, \sigma$ and $L_{j}$.

For example, we consider the case where $\Omega =(0,L)$. The eigenvalues $\rho _{k}$ and eigenvectors $e_{k}$ of (12) are given by

$$\begin{aligned} \rho _{k}=\frac{(k-1)^{2}\pi ^{2}}{L^{2}},\quad e_{k}=cos\frac{(k-1)\pi }{L}x,\quad k=1,2,3,\cdot \cdot \cdot . \end{aligned}$$

It is clear that $k_{2}\ge 2$, and (27) hold true. We see that

$$\begin{aligned} e_{k}^{2}=cos^{2}\frac{(k_{2}-1)\pi }{L}x=\frac{1}{2}(1+cos\frac{2(k_{2}-1)\pi }{L})=\frac{1}{2}(e_{1}+e_{2k_{2}-1}). \end{aligned}$$

Hence, by (29), we have

$$\begin{aligned} \psi =\xi e_{1}+\eta e_{j},\quad \quad \text {with} \quad j=2k_{2}-1. \end{aligned}$$

(52)

where

$$\begin{aligned}{} & {} \begin{pmatrix} 1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \xi _{1}\\ \xi _{2} \end{pmatrix} = \begin{pmatrix} -\frac{B}{2}\\ \frac{B}{2} \end{pmatrix} \\{} & {} \begin{pmatrix} -\lambda _{2} \rho _{2k_{2}-1}+1 &{} \frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-2}{2} \\ -2&{} -D\rho _{2k_{2}-1}-\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} \end{pmatrix} \begin{pmatrix} \eta _{1}\\ \eta _{2} \end{pmatrix} = \begin{pmatrix} -\frac{B}{2}\\ \frac{B}{2} \end{pmatrix} \\{} & {} B=(D\rho _{k_{2}}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2} ) (D\rho _{k_{2}}\frac{\sigma -\sqrt{\sigma ^{2}-4}}{2}-2\sqrt{\sigma ^{2}-4}-\sigma ). \end{aligned}$$

It is readily to see that

$$\begin{aligned}{} & {} \xi _{1}=\frac{B}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-4}, \\{} & {} \xi _{2}=\frac{-B}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-4}, \\{} & {} \eta _{1}=\frac{B}{4} (\frac{D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2}}{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}-(1-\lambda _{2}\rho _{2k_{2}-1})(D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})} -1), \\{} & {} \eta _{2}=\frac{1+\lambda _{2}\rho _{2k_{2}-1}}{2(\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4})-(1-\lambda _{2}\rho _{2k_{2}-1})(2D\rho _{2k_{2}-1}+\frac{\sigma ^{2}+\sigma \sqrt{\sigma ^{2}-4}}{2})} \end{aligned}$$

Inserting (52) and $\xi _{1}$, $\xi _{2}$, $\eta _{1}$, $\eta _{2}$ into (28), we can get the explicit expression of $b_{1}$.

Appendices

Appendix A

$$\begin{aligned} \begin{aligned}&a_{20}=\frac{\langle G_{2}(\xi ,\xi ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle }= \frac{\int _{\Omega }e_{k_{1}}^{3}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\frac{2\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}})\\&\quad \qquad -\frac{2\varepsilon ^{2}}{\sigma }+\sigma (1-\frac{1}{\varepsilon })) \\ {}&a_{11}=\frac{\langle G_{2}(\xi ,\eta )+ G_{2}(\eta ,\xi ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{3}dx}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\sigma (1-\frac{1}{\varepsilon })-\frac{2\varepsilon }{\sigma }(D\rho _{k_{1}}+\varepsilon )), \\ {}&a_{02}=\frac{\langle G_{2}(\eta ,\eta ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } =\frac{\int _{\Omega }e_{k_{1}}^{3}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\sigma (1-\frac{1}{\varepsilon })\\&\quad \qquad -\frac{2\varepsilon }{\sigma }(\alpha _{0}+D\rho _{k_{1}}+\varepsilon )), \\ {}&a_{03}=\frac{\langle G_{3}(\xi ,\xi ,\xi ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\varepsilon -1)(\alpha _{0}-D\rho _{k_{1}}-\varepsilon ), \\ {}&a_{21}=\frac{\langle G_{3}(\xi ,\xi ,\eta )+ G_{3}(\xi ,\eta ,\xi )+ G_{3}(\eta ,\xi ,\xi ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\varepsilon -1)(\alpha _{0}-3D\rho _{k_{1}}-3\varepsilon ), \\&a_{12}=\frac{\langle G_{3}(\xi ,\eta ,\eta )+ G_{3}(\eta ,\eta ,\xi )+ G_{3}(\eta ,\xi ,\eta ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\varepsilon -1)(-\alpha _{0}-3D\rho _{k_{1}}-3\varepsilon ), \\ {}&a_{30}=\frac{\langle G_{3}(\eta ,\eta ,\eta ),\xi ^{*}\rangle }{\langle \xi , \xi ^{*}\rangle } =\frac{-\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (\alpha _{0}+D\rho _{k_{1}}+1)(\varepsilon -1)(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ), \\&b_{20}=\frac{\langle G_{2}(\xi ,\xi ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle }= \frac{\int _{\Omega }e_{k_{1}}^{3}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\frac{2\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-\varepsilon )\\&\quad \qquad +\sigma (1-\frac{1}{\varepsilon })), \\ {}&b_{11}=\frac{\langle G_{2}(\xi ,\eta )+ G_{2}(\eta ,\xi ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{3}dx}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\sigma (1-\frac{1}{\varepsilon })-\frac{\varepsilon }{\sigma }(2D\rho _{k_{1}}+\varepsilon )), \\ {}&b_{02}=\frac{\langle G_{2}(\eta ,\eta ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } \frac{\int _{\Omega }e_{k_{1}}^{3}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\sigma (1-\frac{1}{\varepsilon })\\&\quad \qquad -\frac{2\varepsilon }{\sigma }(\alpha _{0}+D\rho _{k_{1}}+\varepsilon )), \\&b_{03}=\frac{\langle G_{3}(\xi ,\xi ,\xi ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\varepsilon -1)(\alpha _{0}-D\rho _{k_{1}}-\varepsilon ), \\ {}&b_{21}=\frac{\langle G_{3}(\xi ,\xi ,\eta )+ G_{3}(\xi ,\eta ,\xi )+ G_{3}(\eta ,\xi ,\xi ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\varepsilon -1)(\alpha _{0}-3D\rho _{k_{1}}-3\varepsilon ), \\ {}&b_{12}=\frac{\langle G_{3}(\xi ,\eta ,\eta )+ G_{3}(\eta ,\eta ,\xi )+ G_{3}(\eta ,\xi ,\eta ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } \\ {}&\qquad =\frac{\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\varepsilon -1)(-\alpha _{0}-3D\rho _{k_{1}}-3\varepsilon ), \\ {}&a_{30}=\frac{\langle G_{3}(\eta ,\eta ,\eta ),\eta ^{*}\rangle }{\langle \eta , \eta ^{*}\rangle } =\frac{-\int _{\Omega }e_{k_{1}}^{4}dx}{2\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx} (D\rho _{k_{1}}-\alpha _{0}+1)(\varepsilon -1)(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ), \end{aligned} \end{aligned}$$

Appendix B

$$\begin{aligned} \begin{aligned}&\widetilde{a}_{30}=\frac{\alpha _{0}+D\rho _{k_{1}}+1}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx}[\frac{\varepsilon }{\sigma } (\varepsilon -1)\sum _{i=1}^{3} g_{i1}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +(\frac{\sigma }{\varepsilon } (\varepsilon -1)+\frac{\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-1))\sum _{i=1}^{3} g_{i1}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx], \\ {}&\widetilde{a}_{12}=\frac{\alpha _{0}+D\rho _{k_{1}}+1}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx}[\frac{\varepsilon }{\sigma } (\varepsilon -1)\sum _{i=1}^{3} g_{i3}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx+ \\ {}&\quad \quad (\frac{\sigma }{\varepsilon } (\varepsilon -1)+\frac{\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-1))\sum _{i=1}^{3} g_{i3}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +\frac{\varepsilon }{\sigma } (\varepsilon -1)\sum _{i=1}^{3} g_{i2}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx+ \\ {}&\quad \quad (\frac{\sigma }{\varepsilon } (\varepsilon -1)+\frac{\varepsilon }{\sigma }(\alpha _{0}-D\rho _{k_{1}}-1))\sum _{i=1}^{3} g_{i2}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx] \\ {}&\widetilde{b}_{30}=\frac{\alpha _{0}+D\rho _{k_{1}}+1}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx}[(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{\varepsilon }{\sigma }(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ))\sum _{i=1}^{3} g_{i3}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +\frac{\varepsilon }{\sigma }(\varepsilon -1)\sum _{i=1}^{3} g_{i3}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx], \\&\widetilde{b}_{21}=\frac{\alpha _{0}+D\rho _{k_{1}}+1}{\alpha _{0}\int _{\Omega }e_{k_{1}}^{2}dx}[(\frac{\sigma }{\varepsilon } (\varepsilon -1)-\frac{\varepsilon }{\sigma }(\alpha _{0}+D\rho _{k_{1}}+\varepsilon ))\sum _{i=1}^{3} g_{i1}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +\frac{\varepsilon }{\sigma } (\varepsilon -1)\sum _{i=1}^{3} g_{i1}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +(\frac{\varepsilon }{\sigma } (\varepsilon -1)+\frac{\sigma }{\varepsilon }(\alpha _{0}-D\rho _{k_{1}}-\varepsilon ))\sum _{i=1}^{3} g_{i2}\int _{\Omega }E_{i}e_{k_{1}}^{2}dx \\ {}&\quad \quad +\frac{\varepsilon }{\sigma } (\varepsilon -1)\sum _{i=1}^{3} g_{i2}\int _{\Omega }F_{i}e_{k_{1}}^{2}dx]. \end{aligned} \end{aligned}$$